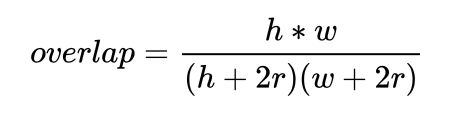目标检测:CenterNet论文解读及代码详解
论文思想
当前anchor-based目标检测方法可分one-stage、two-stage两种。one-stage模型利用anchor机制得到大量的框,之后直接加入回归、分类分支对框进行分类与微调。two-stage模型则首先提出大量的候选框,使召回率达到最大,之后在第二个stage对这些候选框进行分类与回归。无论是one-stage还是two-stage方法都存在大量的计算资源浪费和必须后处理(nms)的问题,从而无法实现end-to-end。
本篇论文的作者提出了一种anchor-free的目标检测方法,其思想非常的简洁高效:
- 用目标框中心点表示物体
- 使用中心点位置的特征预测中心点offset和目标框的长、宽
- 每个中心点只产生一个框,从而无需nms后处理,实现真正的end-to-end
模型结构
根据mmdetection中centernet的config和论文中的描述,我绘制了如下的网络结构。backbone部分使用resnet-18,neck部分并未采用fpn而是采用了三次上采样,将backbone部分输出的512*(w/32)(h/32)的feature map恢复成64(w/4)*(h/4)的大小,这样做的目的是即得到高层丰富的语义信息又可以得到高分辨率的输出。最后head部分使用了三个head,分别是:heatmap head、offset head、wh head。heatmap head有c个通道,c代表类别数,每个数字代表当前为ci类别的物体中心点的概率,因此heatmap feature是经过sigmoid处理后的结果。wh head有两个通道,分别代表了由相对应heatmap点预测的到的bbox的宽和高。offest head的通道数也为2,分别代表相对应heatmap点预测得到的中心点的偏移量。

Train
论文针对三个head设计了三个loss进行学习,对于heatmap head使用Gaussian focal loss,对于wh head和offset head则使用L1 loss。本文仅对Gaussian focal loss部分进行深入讲解。首先需要解决的问题是如何的到gt heatmap,因为目标检测数据集的label只是类别和框的位置信息。我们可以看mmdetection对这个问题的源码实现:
def get_targets(self, gt_bboxes, gt_labels, feat_shape, img_shape):
"""Compute regression and classification targets in multiple images.
Args:
gt_bboxes (list[Tensor]): Ground truth bboxes for each image with
shape (num_gts, 4) in [tl_x, tl_y, br_x, br_y] format.
gt_labels (list[Tensor]): class indices corresponding to each box.
feat_shape (list[int]): feature map shape with value [B, _, H, W]
img_shape (list[int]): image shape in [h, w] format.
Returns:
tuple[dict,float]: The float value is mean avg_factor, the dict has
components below:
- center_heatmap_target (Tensor): targets of center heatmap, \
shape (B, num_classes, H, W).
- wh_target (Tensor): targets of wh predict, shape \
(B, 2, H, W).
- offset_target (Tensor): targets of offset predict, shape \
(B, 2, H, W).
- wh_offset_target_weight (Tensor): weights of wh and offset \
predict, shape (B, 2, H, W).
"""
img_h, img_w = img_shape[:2]
bs, _, feat_h, feat_w = feat_shape
width_ratio = float(feat_w / img_w)
height_ratio = float(feat_h / img_h)
center_heatmap_target = gt_bboxes[-1].new_zeros(
[bs, self.num_classes, feat_h, feat_w])
wh_target = gt_bboxes[-1].new_zeros([bs, 2, feat_h, feat_w])
offset_target = gt_bboxes[-1].new_zeros([bs, 2, feat_h, feat_w])
wh_offset_target_weight = gt_bboxes[-1].new_zeros(
[bs, 2, feat_h, feat_w])
for batch_id in range(bs):
gt_bbox = gt_bboxes[batch_id]
gt_label = gt_labels[batch_id]
center_x = (gt_bbox[:, [0]] + gt_bbox[:, [2]]) * width_ratio / 2
center_y = (gt_bbox[:, [1]] + gt_bbox[:, [3]]) * height_ratio / 2
gt_centers = torch.cat((center_x, center_y), dim=1)
for j, ct in enumerate(gt_centers):
ctx_int, cty_int = ct.int()
ctx, cty = ct
scale_box_h = (gt_bbox[j][3] - gt_bbox[j][1]) * height_ratio
scale_box_w = (gt_bbox[j][2] - gt_bbox[j][0]) * width_ratio
radius = gaussian_radius([scale_box_h, scale_box_w],
min_overlap=0.3)
radius = max(0, int(radius))
ind = gt_label[j]
gen_gaussian_target(center_heatmap_target[batch_id, ind],
[ctx_int, cty_int], radius)
wh_target[batch_id, 0, cty_int, ctx_int] = scale_box_w
wh_target[batch_id, 1, cty_int, ctx_int] = scale_box_h
offset_target[batch_id, 0, cty_int, ctx_int] = ctx - ctx_int
offset_target[batch_id, 1, cty_int, ctx_int] = cty - cty_int
wh_offset_target_weight[batch_id, :, cty_int, ctx_int] = 1
avg_factor = max(1, center_heatmap_target.eq(1).sum())
target_result = dict(
center_heatmap_target=center_heatmap_target,
wh_target=wh_target,
offset_target=offset_target,
wh_offset_target_weight=wh_offset_target_weight)
return target_result, avg_factor
直接看docstring和注释其实不难理解这个函数在做什么,实际上就是根据ground truth的bbox得到center,之后根据feature 和原图的比例关系ratio将center的位置映射到heatmap feature上,例如上面我自己绘制的网络结构,ratio=1/4。但是仔细看代码,显然center_heatmap_target不是简单令映射后center位置为1其他位置皆为0,而是使用了gaussian_radius和gen_gaussian_target两个函数得到最终结果,为什么要这么做呢?
有请小猫咪出场!
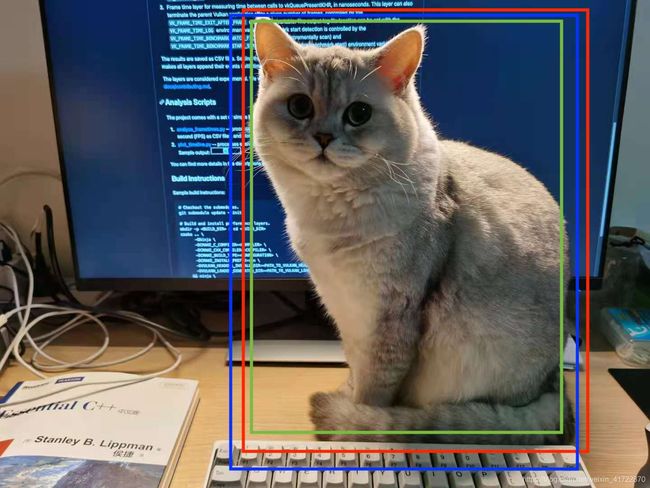
图中红色框是ground truth,但是显然蓝色框和绿色框也是可接受的预测框,那么如果我们生硬的将center设置为1其他位置都变成0,那么类似蓝色、绿色这样的框都会被“阉割”掉,这样的方法肯定是不够合理的。CenterNet中针对这个问题采取了和CornerNet中类似的方法,我们来看CornerNet中作者的描述:

根据论文的描述,CornerNet中当预测的corners在top-left/bottom-right点的某一个半径r内,我们并非直接不要这些corner(不置0)而是通过二维的高斯核来实现慢慢的过渡。具体操作方法就是通过ground truth的size计算高斯散射核的半径,例如计算得到的半径为1,那么高斯核的大小为3*3,令gt corner的位置为中心设置为1,周围位置以
递减。那么最终得到的高斯核如下:

这样再来看论文中给出的Gaussian focal loss公式

当gt的高斯核值为1时,被认正样本,当其接近于1时则对negative focal loss进行抑制,这样就能考虑到那些接近于gt的可以接受的bbox。以上内容查看mmdetection中gen_gaussian_target()函数和gaussian2D()便可以更清晰的理解
def gaussian2D(radius, sigma=1, dtype=torch.float32, device='cpu'):
"""Generate 2D gaussian kernel.
Args:
radius (int): Radius of gaussian kernel.
sigma (int): Sigma of gaussian function. Default: 1.
dtype (torch.dtype): Dtype of gaussian tensor. Default: torch.float32.
device (str): Device of gaussian tensor. Default: 'cpu'.
Returns:
h (Tensor): Gaussian kernel with a
``(2 * radius + 1) * (2 * radius + 1)`` shape.
"""
x = torch.arange(
-radius, radius + 1, dtype=dtype, device=device).view(1, -1)
y = torch.arange(
-radius, radius + 1, dtype=dtype, device=device).view(-1, 1)
h = (-(x * x + y * y) / (2 * sigma * sigma)).exp()
h[h < torch.finfo(h.dtype).eps * h.max()] = 0
return h
def gen_gaussian_target(heatmap, center, radius, k=1):
"""Generate 2D gaussian heatmap.
Args:
heatmap (Tensor): Input heatmap, the gaussian kernel will cover on
it and maintain the max value.
center (list[int]): Coord of gaussian kernel's center.
radius (int): Radius of gaussian kernel.
k (int): Coefficient of gaussian kernel. Default: 1.
Returns:
out_heatmap (Tensor): Updated heatmap covered by gaussian kernel.
"""
diameter = 2 * radius + 1
gaussian_kernel = gaussian2D(
radius, sigma=diameter / 6, dtype=heatmap.dtype, device=heatmap.device)
x, y = center
height, width = heatmap.shape[:2]
left, right = min(x, radius), min(width - x, radius + 1)
top, bottom = min(y, radius), min(height - y, radius + 1)
masked_heatmap = heatmap[y - top:y + bottom, x - left:x + right]
masked_gaussian = gaussian_kernel[radius - top:radius + bottom,
radius - left:radius + right]
out_heatmap = heatmap
torch.max(
masked_heatmap,
masked_gaussian * k,
out=out_heatmap[y - top:y + bottom, x - left:x + right])
return out_heatmap
比较难理解的是如何的到合适的高斯半径?计算高斯半径目的是为了让预测center出现在gt center的某个半径范围内时,其结果仍能满足iou大于某个min overlap。这里计算半径的方法直接沿用了corner net中的方法,其计算考虑了以下三种情形:(红色为gt, 黑色为bbox)
对于第三种情况可能大家会和我产生相同的疑惑,这样计算明显是不正确的,但为什么要这样计算呢?包括mmdetection中对应的实现也是这样计算的。我个人理解这样做主要是计算起来方便,所以做了近似,在cornernet中有对于这个问题的讨论,似乎更换了公式后训练效果并未有明显提升。
def gaussian_radius(det_size, min_overlap):
r"""Generate 2D gaussian radius.
This function is modified from the `official github repo
`_.
Given ``min_overlap``, radius could computed by a quadratic equation
according to Vieta's formulas.
There are 3 cases for computing gaussian radius, details are following:
- Explanation of figure: ``lt`` and ``br`` indicates the left-top and
bottom-right corner of ground truth box. ``x`` indicates the
generated corner at the limited position when ``radius=r``.
- Case1: one corner is inside the gt box and the other is outside.
.. code:: text
|< width >|
lt-+----------+ -
| | | ^
+--x----------+--+
| | | |
| | | | height
| | overlap | |
| | | |
| | | | v
+--+---------br--+ -
| | |
+----------+--x
To ensure IoU of generated box and gt box is larger than ``min_overlap``:
.. math::
\cfrac{(w-r)*(h-r)}{w*h+(w+h)r-r^2} \ge {iou} \quad\Rightarrow\quad
{r^2-(w+h)r+\cfrac{1-iou}{1+iou}*w*h} \ge 0 \\
{a} = 1,\quad{b} = {-(w+h)},\quad{c} = {\cfrac{1-iou}{1+iou}*w*h}
{r} \le \cfrac{-b-\sqrt{b^2-4*a*c}}{2*a}
- Case2: both two corners are inside the gt box.
.. code:: text
|< width >|
lt-+----------+ -
| | | ^
+--x-------+ |
| | | |
| |overlap| | height
| | | |
| +-------x--+
| | | v
+----------+-br -
To ensure IoU of generated box and gt box is larger than ``min_overlap``:
.. math::
\cfrac{(w-2*r)*(h-2*r)}{w*h} \ge {iou} \quad\Rightarrow\quad
{4r^2-2(w+h)r+(1-iou)*w*h} \ge 0 \\
{a} = 4,\quad {b} = {-2(w+h)},\quad {c} = {(1-iou)*w*h}
{r} \le \cfrac{-b-\sqrt{b^2-4*a*c}}{2*a}
- Case3: both two corners are outside the gt box.
.. code:: text
|< width >|
x--+----------------+
| | |
+-lt-------------+ | -
| | | | ^
| | | |
| | overlap | | height
| | | |
| | | | v
| +------------br--+ -
| | |
+----------------+--x
To ensure IoU of generated box and gt box is larger than ``min_overlap``:
.. math::
\cfrac{w*h}{(w+2*r)*(h+2*r)} \ge {iou} \quad\Rightarrow\quad
{4*iou*r^2+2*iou*(w+h)r+(iou-1)*w*h} \le 0 \\
{a} = {4*iou},\quad {b} = {2*iou*(w+h)},\quad {c} = {(iou-1)*w*h} \\
{r} \le \cfrac{-b+\sqrt{b^2-4*a*c}}{2*a}
Args:
det_size (list[int]): Shape of object.
min_overlap (float): Min IoU with ground truth for boxes generated by
keypoints inside the gaussian kernel.
Returns:
radius (int): Radius of gaussian kernel.
"""
height, width = det_size
a1 = 1
b1 = (height + width)
c1 = width * height * (1 - min_overlap) / (1 + min_overlap)
sq1 = sqrt(b1**2 - 4 * a1 * c1)
r1 = (b1 - sq1) / (2 * a1)
a2 = 4
b2 = 2 * (height + width)
c2 = (1 - min_overlap) * width * height
sq2 = sqrt(b2**2 - 4 * a2 * c2)
r2 = (b2 - sq2) / (2 * a2)
a3 = 4 * min_overlap
b3 = -2 * min_overlap * (height + width)
c3 = (min_overlap - 1) * width * height
sq3 = sqrt(b3**2 - 4 * a3 * c3)
r3 = (b3 + sq3) / (2 * a3)
return min(r1, r2, r3)
最后我们来说下为什么要有offset map,这是因为当gt的center根据缩放关系映射到feature map之后,需要做int操作,这样造成一些偏差,因此需要offset map来调整中心点位置。
Inference
在inference的过程中,我们得到了heatmap、wh、 offset三个head的输出之后,首先要筛选出heatmap中每个channel的峰值点,代表此点是物体的中心点。具体做法就是使用kernel_size=3的kernel在map上做maxpooling,提取topk的峰值点。之后根据wh map、offset map峰值点对应位置的信息的到预测bbox的结果。

这里思路还是比较清晰的,值得注意的是,由于所有的输出都直接从关键点估计得到,无需基于IOU的NMS或者其他后处理。
centernet的优缺点
优点:
- anchor free,减少了计算资源浪费
- 无需nms,实现真正的end-to-end
- 模型简洁高效,同等条件下,fps表现优于yolov3
- 可以比较方便的拓展到除了目标检测以外的任务
缺点:
- 对于中心点重叠的问题缺少处理方法