读论文(7)——CenterNet
前言
回顾我们之前学习的目标检测方法,无论是单阶段方法还是双阶段方法,都是通过对目标框(anchor)进行预测来进行目标检测。换句话说,之前的方法都是以框来代表目标,然后再对框进行分类,这样就将目标检测问题退化成了一个分类问题。我们可以发现,之前我们学过的哪些方法,无论模型怎么变,这个思路始终都是如此。但是基于这个这个思路的主流框架往往都需要预先设置框,然后对每个框都进行分类,这样开销相对较大。那么我们可不可以从根本上就推翻这个目标检测的思路呢?这次要读的CenterNet就是一个在根本思路、在大方向上的创新。
思路
CenterNet原作名称为《Objects as Points》。顾名思义,这是一个用点来代表目标的方法。CenterNet借鉴了人体关键点检测的一些思路与方法,先把所有的类别都列出来,然后分别检测每个类别在图中的那个部分有对应的目标,这个目标用关键点来表示,然后再由关键点去生成目标框。这种方法本质上就是把目标检测问题退化成了一个关键点估计问题。这么做的好处是什么呢?个人认为,这样做使得每一个标出来的关键点都是一个有应检测出的目标的正样本,就不会像以往预先设置anchor框的那些方法一样去处理一些没有目标(背景)的部分,这样开销相对的会有所减少,正负样本数目也会相对平衡,最关键的是,这种思路经过一些池化处理后,可以抛弃NMS,实现完全端到端。
实际上,最早丢掉anchor框进行预测的方法是CornerNet,这种方法是通过检测目标框的左上角和右下角两个关键点得到预测框,但这种方式会会不可避免的发生一些错误,且要经过一个角点的匹配阶段,增加了开销。因此文章化繁为简,直接对关键点进行检测,不涉及匹配问题等一系列后处理,还让精度提高了。
另外,还有一篇和本文介绍的方法同时代的、名为《CenterNet: Keypoint Triplets for Object Detection》的论文也可以被称为CenterNet,这篇论文主要是在 CornerNet 的基础上发展而来,通过构建三元组(左上角、右下角和中心点结合)进行物体检测,感兴趣的朋友们可以阅读一下。
寻找关键点
我们知道,CenterNet的最核心的部分就是用关键点代替anchor进行目标检测,那么是怎么找到这个关键点的呢?
答案是利用热力图,将图像输入CNN得到对应的热力图,热力图的峰值就对应目标的关键点,然后目标框就以这个关键点为中心进行预测。
假设输入图像 I I I为W×H×3,然后我们要得到这张图片的热力图 Y ^ \hat{Y} Y^为W/R×H/R×C,其中 Y ^ \hat{Y} Y^为的取值范围为[0,1],R为步长(本文一般取4),C是在目标检测中对应着检测类别的数量。
我们可以得知, Y ^ x , y , c \hat{Y}_{x,y,c} Y^x,y,c= 1的点就表明在当前坐标中检测到了属于类别C的物体, Y ^ x , y , c \hat{Y}_{x,y,c} Y^x,y,c = 0的点就是当前坐标不含类别C。
那么,如何从图像 I I I得到热力图 Y ^ \hat{Y} Y^呢?
**从采用模型上说,**本文采用了ResNet、DLA、Hourglass这几种不同的网络模型,并做出了对比,有关这方面我们将在网络结构部分介绍。
而就具体思路步骤来说, 在训练过程中,对于每个ground truth中的某一类C,我们要将真实关键点(true keypoint) 计算出来。作者借助了CornerNet的方法,让 ( x 1 ( k ) , y 1 ( k ) , x 2 ( k ) , y 2 ( k ) ) (x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)}) (x1(k),y1(k),x2(k),y2(k))这对角线上的两点,作为 c k c_k ck类的目标k,因此,原尺寸的keypoint就可以定位为 p = ( x 1 + x 2 2 , y 1 + y 2 2 ) p=(\frac{x1+x2}{2},\frac{y1+y2}{2}) p=(2x1+x2,2y1+y2),然后进行下采样后可以得到低分辨率等价的 p ~ = ⌊ p R ⌋ \tilde{p}=\lfloor \frac{p}{R} \rfloor p~=⌊Rp⌋,之后把所有的ground truth分布在一个热力图 Y ∈ [ 0 , 1 ] ( W / R ) × ( H / R ) × C Y\in[0,1]^{(W/R)×(H/R)×C} Y∈[0,1](W/R)×(H/R)×C上,并使用一个高斯卷积核 Y x y c Y_{xyc} Yxyc将关键点分布到特征图上,这个高斯卷积核如下:
![]()
其中 σ p \sigma_p σp 是一个与目标大小相关的标准差。如果某一个类的两个高斯分布发生了重叠,直接取每个元素最大值就可以。
Y ∈ [ 0 , 1 ] ( W / R ) × ( H / R ) × C Y\in[0,1]^{(W/R)×(H/R)×C} Y∈[0,1](W/R)×(H/R)×C为1则代表是这个目标的中心点,也就是我们要预测要学习的点。
我们对上面这一段操作做一个总结:
送入网络的图片尺寸为512x512,生成的热力图尺寸为128x128。需要经历如下步骤:
(1)将目标的ground truth box缩放到128x128的尺度上,然后求其的中心点坐标并取整,设为truth keypoint;
(2)根据目标ground truth box大小计算高斯圆的半径,设为r
(3)在热力图上,以truth keypoint为圆心,半径为r填充高斯函数计算值。(truth keypoint点处为最大值,沿着半径向外按高斯函数递减)
官方源码中生成的一个高斯分布如下所示:

一个生成热力图的例子如下所示(注意热力图是对每个特定类生成的):

损失函数
下面我们来补充一下关键点预测中对损失函数的理解,这个总的损失函数可以写作:
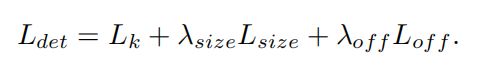
L k L_k Lk是损失函数的主体,我们可以理解为是热力图的loss,采用如下形式:
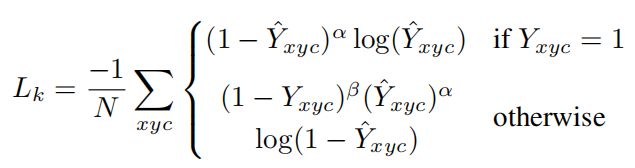
可以看出,这个形式实际上就是我们上篇看过的focal loss的一种变式,α和β是超参数,用来均衡难易样本和正负样本,论文中分别取2和4。N是图像的关键点数量,用于将所有的positive focal loss标准化为1。 Y ^ x y c \hat{Y}_{xyc} Y^xyc是预测值,而 Y x y c Y_{xyc} Yxyc为标注值。
观察这个loss,当 Y x y c Y_{xyc} Yxyc为1时,也就是标注的真实值为1,这个点是一个关键点,这时如果 Y ^ x y c \hat{Y}_{xyc} Y^xyc接近1,则 ( 1 − Y ^ x y c ) α (1-\hat{Y}_{xyc})^{\alpha} (1−Y^xyc)α就会趋近于0,说明对于一个易分类样本,其在损失中的占的权重会变少;而如果 Y ^ x y c \hat{Y}_{xyc} Y^xyc接近0,则其权重被保留(仍然接近1),说明对于这个点,还没有学习正确,需要加大学习力度——这就是focal loss的思想。
但是当 Y x y c Y_{xyc} Yxyc不为1时,也就是该点不是真实的关键点,这时在原来的focal loss的基础上增加了 ( 1 − Y x y c ) β (1-Y_{xyc})^{\beta} (1−Yxyc)β一项作为修正,这一项一定是在0到1之间的,除非 Y x y c Y_{xyc} Yxyc为0,否则经过β次方(β=4)后这一项会变得更小,个人认为这一步是为了抑制0< Y x y c Y_{xyc} Yxyc<1这一部分负样本的loss,也就是抑制关键点附近的的那些点的loss,因为他们离着关键点越近,越不能代表不是关键点的负样本的情况,因此削弱这一部分的影响。
为了弥补由输出步长造成的量化误差,文章对每个关键点额外预测了一个定位的偏移量,记为 O ^ p ~ \hat{O}_{\tilde{p}} O^p~,一个目标的所有的类别c共享相同的预测偏移量,损失采用L1 loss的形式,如下所示:
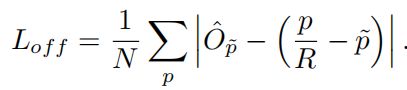
我们前一个部分提到, p ~ = ⌊ p R ⌋ \tilde{p}=\lfloor \frac{p}{R} \rfloor p~=⌊Rp⌋, ( p R − p ~ ) (\frac{p}{R}-\tilde{p}) (Rp−p~)表示转成低分辨率之后点和原来直接下采样大图之后坐标的误差。我们通过训练这样的偏移量 O ^ p ~ \hat{O}_{\tilde{p}} O^p~来弥补这部分误差。
我们最终的目的不是仅仅把关键点找出来,还需要把目标给框出来,因此还有一部分损失是对于框的长宽预测的,这一部分记作 L s i z e L_{size} Lsize,只对正样本的损失值计算(因为负样本没有框),同样采用L1 loss,如下所示:

其中 S ^ p k \hat{S}_{p_k} S^pk为预测的尺寸, s k s_k sk是真实的尺寸,计算方式为 s k = ( x 2 ( k ) − x 1 ( k ) , y 2 ( k ) − y 1 ( k ) ) s_k=({x_2}^{(k)}-{x_1}^{(k)},{y_2}^{(k)}-{y_1}^{(k)}) sk=(x2(k)−x1(k),y2(k)−y1(k))。
最后通过加权得出最后的损失函数,论文中 λ o f f \lambda_{off} λoff取1, λ s i z e \lambda_{size} λsize取0.1。
由点得到框
上一部分我们说了,得到关键点不是最终目的,最终目的还是要能把物体给框出来,那么如何由关键点得到框呢?
在推理阶段,论文对每个类别先独立地提取热力图上的峰值点。具体方法是检测所有比周围八临域都大的像素点,论文中使用的是3x3的最大池化,就类似于anchor-based检测方法中NMS的效果。
第c类检测出的一个点记为:
![]()
每个点的坐标用 ( x i , y i ) (x_i,y_i) (xi,yi)表示,那么预测框可以表示为:

其中 ( δ x ^ i , δ y ^ i ) (\delta\hat{x}_{i},\delta\hat{y}_{i}) (δx^i,δy^i)就是损失函数中提到的 O ^ , \hat{O}, O^,表示预测的位置偏移量; ( w i , h i ) (w_i,h_i) (wi,hi)就是预测出来的尺寸 S ^ \hat{S} S^。
预测完框后,我们把该框中心点处的热力图值 Y ^ x i y i c \hat{Y}_{x_{i}y_{i}c} Y^xiyic看作是该框的置信度。
网络结构
最后来看一下实现这些的backbone网络。本文一共尝试了3种网络框架,分别是Hourglass,ResNet和DLA。
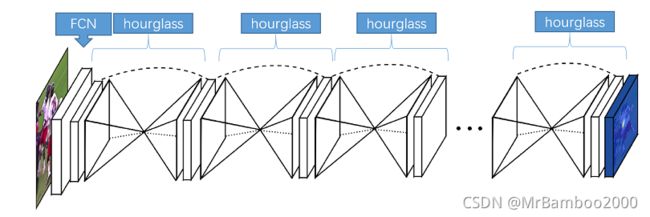
(1)Hourglass网络
这是一种结构形状为沙漏状,重复使用top-down和bottom-up(先降采样再升采样),来推断关键点位置的网络。如下图所示:
Hourglass采用模块化设计的思想,由残差块构成子网再由子网拼接称网络,hourglass模块结构如下图所示:
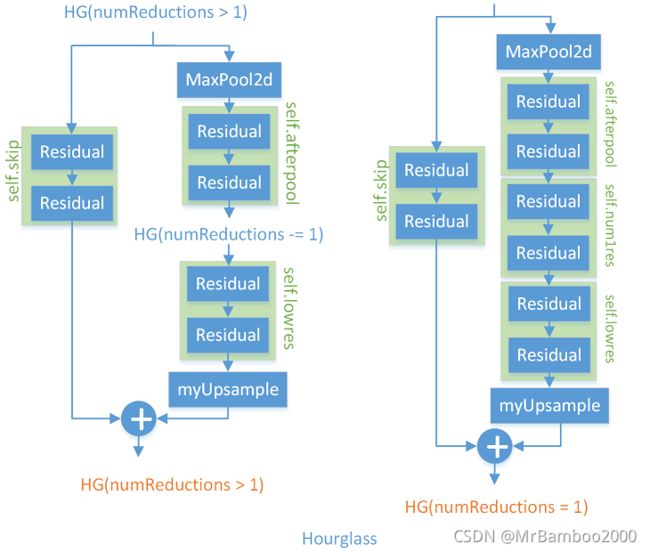
可以看出升采样的过程是结合跳级结构辅助进行的。
在CenterNet中,堆叠的Hourglass网络通过两个连续的hourglass模块对输入进行了4倍的下采样,每个hourglass模块是个对称的5层下和上卷积网络,且带有skip连接。**该网络较大,但通常会生成最好的关键点估计。**具体效果如本部分最后的表所示。
(2)ResNet网络
本文对标准的ResNet做了3个上卷积网络来得到更高的分辨率输出。为了节省计算量,这3个上卷积的输出通道数分别设置为256,128,64。上卷积核初始为双线性插值。
本文对ResNet-18和ResNet-101都进行了测试,结果如本部分最后的表所示。
(3)DLA
DLA全称是Deep Layer Aggregation。Aggretation聚合是目前设计网络结构的常用的一种技术。DLA主要解决将不同深度,将不同stage、block之间的信息进行融合。之前的ResNet利用skip connection进行融合,但这种融合方式仅限于块内部,并且融合方式仅限于简单的叠加。DLA则能够迭代式地将网络结构的特征信息融合起来,让模型有更高的精度和更少的参数。
DLA的设计思路是通过来自DenseNet的Dense Connections聚合语义信息通过Feature Pyramids空间特征金字塔聚合空间信息,通过DLA将两者更好地结合起来从而更好的获取what和where的信息。如下图所示:

本文采用baseline的是DLA-34,其完整结构如下所示:
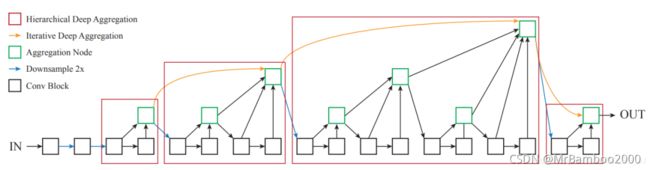
本文将将原来上采样层的卷积都替换成3x3的deformable卷积。在每个输出head前加了一个3x3x256的卷积,然后做1x1卷积得到期望输出。
精度如最后的表所示。
(4)效果对比

可以看出Hourglass的精度是最高的,DLA次之,ResNet再次。但是Hourglass的实时性是最差的,具体来说Hourglass只能达到1.4FPS,但DLA-34可以达到52FPS,ResNet更是可以达到惊人的142FPS。
此外,我们注意到作者还对数据增强带来的效果进行了对比,表中的N.A.即是不做增强,F表示做了翻转变换,MA则表示在翻转变换的基础上又做了多尺度的变换。可以发现,数据增强对精度是有一定改进的。
总结
其实这篇文章还说明了CenterNet方法可以应用于3D检测和人体姿态估计,而且都可以和sota方法相媲美,感兴趣的同学们可以阅读原始论文,这里不再赘述。应当说,CenterNet为代表的一类anchor-free方法为目标检测在大方向上又提供了一个新的思路,我们可以抛弃掉anchor的思想用点去进行检测,抛弃掉将目标检测转为框内物体分类的思想方法,用将目标检测转为关键点检测的思想方法。当然这种方法目前也有弊端——训练时长较长,还需要后人去探索改进。
