深度学习 | 吴恩达深度学习课程2 Week1
Course2 Week1 编程作业
- 1 任务
- 2 初始化参数
-
- 2.1 数据
- 2.2 神经网络模型
- 2.3 初始化为零
-
- 2.3.1 代码
- 2.3.2 训练
- 2.3.3 预测
- 2.4 随机初始化
-
- 2.4.1 代码
- 2.4.2 训练
- 2.4.3 预测
- 2.5 抑梯度异常初始化
-
- 2.5.1 代码
- 2.5.2 训练
- 2.5.3 预测
- 2.6 总结
- 3 正则化
-
- 3.1 数据
- 3.2 代码
- 3.3 训练+预测
- 4 dropout
-
- 4.1 代码
-
- 4.1.1前向
- 4.1.2 反向
- 4.1.3 主代码
- 4.2 训练+预测
- 5 梯度校验
-
- 5.1 一维情形
-
- 5.1.1 前向传播
- 5.1.2 反向传播
- 5.1.3 梯度校验
- 5.1.4 测试
- 5.2 高维情形
-
- 5.2.1 前向传播+反向传播
- 5.2.2 梯度校验
- 参考
1 任务
-
初始化参数:
1.1:使用0来初始化参数。
1.2:使用随机数来初始化参数。
1.3:使用抑梯度异常初始化参数(参见视频中的梯度消失和梯度爆炸)。
-
正则化模型:
2.1:使用二范数对二分类模型正则化,尝试避免过拟合。
2.2:使用随机删除节点的方法精简模型,同样是为了尝试避免过拟合。
-
梯度校验 :对模型使用梯度校验,检测它是否在梯度下降的过程中出现误差过大的情况
2 初始化参数
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import init_utils #第一部分,初始化
import reg_utils #第二部分,正则化
import gc_utils #第三部分,梯度校验
#%matplotlib inline #如果你使用的是Jupyter Notebook,请取消注释。
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
2.1 数据
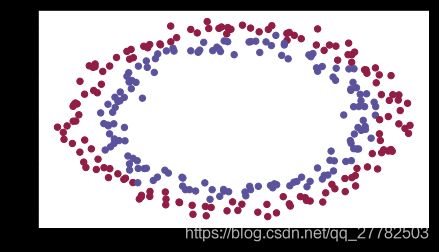
train_X, train_Y, test_X, test_Y = init_utils.load_dataset(is_plot=True)
2.2 神经网络模型
def model(X,Y,learning_rate=0.01,num_iterations=15000,print_cost=True,initialization="he",is_polt=True):
"""
实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
参数:
X - 输入的数据,维度为(2, 要训练/测试的数量)
Y - 标签,【0 | 1】,维度为(1,对应的是输入的数据的标签)
learning_rate - 学习速率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每迭代1000次打印一次
initialization - 字符串类型,初始化的类型【"zeros" | "random" | "he"】
is_polt - 是否绘制梯度下降的曲线图
返回
parameters - 学习后的参数
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0],10,5,1]
#选择初始化参数的类型
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
else :
print("错误的初始化参数!程序退出")
exit
#开始学习
for i in range(0,num_iterations):
#前向传播
a3 , cache = init_utils.forward_propagation(X,parameters)
#计算成本
cost = init_utils.compute_loss(a3,Y)
#反向传播
grads = init_utils.backward_propagation(X,Y,cache)
#更新参数
parameters = init_utils.update_parameters(parameters,grads,learning_rate)
#记录成本
if i % 1000 == 0:
costs.append(cost)
#打印成本
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
#学习完毕,绘制成本曲线
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回学习完毕后的参数
return parameters
2.3 初始化为零
2.3.1 代码
def initialize_parameters_zeros(layers_dims):
"""
将模型的参数全部设置为0
参数:
layers_dims - 列表,模型的层数和对应每一层的节点的数量
返回
parameters - 包含了所有W和b的字典
W1 - 权重矩阵,维度为(layers_dims[1], layers_dims[0])
b1 - 偏置向量,维度为(layers_dims[1],1)
···
WL - 权重矩阵,维度为(layers_dims[L], layers_dims[L -1])
bL - 偏置向量,维度为(layers_dims[L],1)
"""
parameters = {}
L = len(layers_dims) #网络层数
for l in range(1,L):
parameters["W" + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1]))
parameters["b" + str(l)] = np.zeros((layers_dims[l],1))
#使用断言确保我的数据格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l],layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l],1))
return parameters
2.3.2 训练
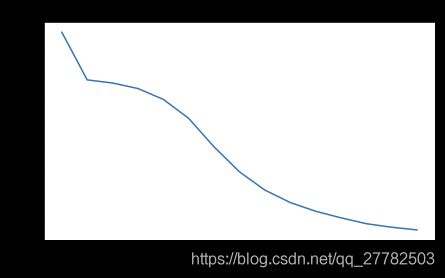
parameters = model(train_X,train_Y,initialization="zeros",is_polt=True)
parameters
第0次迭代,成本值为:0.6931471805599453
第1000次迭代,成本值为:0.6931471805599453
第2000次迭代,成本值为:0.6931471805599453
第3000次迭代,成本值为:0.6931471805599453
第4000次迭代,成本值为:0.6931471805599453
第5000次迭代,成本值为:0.6931471805599453
第6000次迭代,成本值为:0.6931471805599453
第7000次迭代,成本值为:0.6931471805599453
第8000次迭代,成本值为:0.6931471805599453
第9000次迭代,成本值为:0.6931471805599453
第10000次迭代,成本值为:0.6931471805599455
第11000次迭代,成本值为:0.6931471805599453
第12000次迭代,成本值为:0.6931471805599453
第13000次迭代,成本值为:0.6931471805599453
第14000次迭代,成本值为:0.6931471805599453
{'W1': array([[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.],
[0., 0.]]), 'W2': array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]), 'W3': array([[0., 0., 0., 0., 0.]]), 'b1': array([[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.],
[0.]]), 'b2': array([[0.],
[0.],
[0.],
[0.],
[0.]]), 'b3': array([[1.6549262e-16]])}
2.3.3 预测
print ("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print ("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
训练集:
Accuracy: 0.5
测试集:
Accuracy: 0.5
predictions_train
array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
predictions_test
array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
- 可以看到所有预测结果全部预测为0了,所以和瞎猜差不多了,初始化参数为0效果很差!
2.4 随机初始化
2.4.1 代码
def initialize_parameters_random(layers_dims):
"""
将模型的参数随机初始化
参数:
layers_dims - 列表,模型的层数和对应每一层的节点的数量
返回
parameters - 包含了所有W和b的字典
W1 - 权重矩阵,维度为(layers_dims[1], layers_dims[0])
b1 - 偏置向量,维度为(layers_dims[1],1)
···
WL - 权重矩阵,维度为(layers_dims[L], layers_dims[L -1])
bL - 偏置向量,维度为(layers_dims[L],1)
"""
np.random.seed(3) # 指定随机种子
parameters = {}
L = len(layers_dims) #网络层数
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * 10 # 10倍缩放
parameters["b" + str(l)] = np.zeros((layers_dims[l],1)) # b无所谓 可以还是初始化为0
#使用断言确保我的数据格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l],layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l],1))
return parameters
2.4.2 训练
parameters = model(train_X,train_Y,initialization="random",is_polt=True)
parameters
/Users/apple/Desktop/深度学习/课程2-week1/init_utils.py:50: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
/Users/apple/Desktop/深度学习/课程2-week1/init_utils.py:50: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
第0次迭代,成本值为:inf
第1000次迭代,成本值为:0.6250884962121392
第2000次迭代,成本值为:0.5981371467489438
第3000次迭代,成本值为:0.5638539771863162
第4000次迭代,成本值为:0.5501704762630747
第5000次迭代,成本值为:0.5444592806792145
第6000次迭代,成本值为:0.5374509252365552
第7000次迭代,成本值为:0.4760640415643904
第8000次迭代,成本值为:0.3978146724300182
第9000次迭代,成本值为:0.3934785833165248
第10000次迭代,成本值为:0.3920322287285902
第11000次迭代,成本值为:0.38924754816043866
第12000次迭代,成本值为:0.38615976417756703
第13000次迭代,成本值为:0.38498687252939306
第14000次迭代,成本值为:0.38278602219555746
{'W1': array([[ 14.92140093, 3.06527372],
[ 1.19795813, -14.55693233],
[ -2.83827371, -5.49372956],
[ -1.33406802, -5.21612767],
[ 0.83376394, -6.26167795],
[-12.64462965, 10.21578851],
[ 7.75553345, 15.62479886],
[ 3.36741078, -6.1912799 ],
[ -5.38873894, -13.72944281],
[ 8.52176564, -8.49062966]]),
'W2': array([[-11.85147726, -2.05649899, 14.86148355, 2.36716267,
-10.2378514 , -7.05368081, 6.312671 , -1.69016926,
-7.6883635 , -2.30030722],
[ 7.19331997, 17.5632243 , -13.19824528, -7.14650186,
-8.83687847, -24.23898934, -9.34853863, -11.20017628,
9.0501246 , -2.79938306],
[-16.23285446, 6.46675452, -3.56270759, -17.43141037,
-5.96649642, -5.8859438 , -8.73882298, 0.29713815,
-22.48257768, -2.67761865],
[ 6.71885029, 8.16528538, 10.96238971, 11.0585574 ,
14.77062516, -12.16218409, 3.16280517, -18.77346653,
-6.43157584, -19.83194998],
[ 9.17673356, 12.35650445, -2.51211064, 17.34810077,
-7.86616804, 0.91395834, 0.79831804, -13.10973711,
3.29697538, 16.57190501]]),
'W3': array([[-10.24794041, 5.1678546 , -1.54506852, 15.44357046,
-0.52959759]]),
'b1': array([[-4.53824986],
[-4.80379943],
[ 1.19811812],
[-2.45957553],
[ 3.1473294 ],
[ 3.11968047],
[-2.07175549],
[ 7.36870565],
[-1.89078814],
[-2.24148617]]),
'b2': array([[-0.01008132],
[-0.14067763],
[ 0. ],
[-0.35957766],
[-0.32890145]]),
'b3': array([[1.20167094]])}
初步看效果还可以,损失函数在减少,来看看预测结果
2.4.3 预测
print ("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print ("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
训练集:
Accuracy: 0.83
测试集:
Accuracy: 0.86
- 但是使用过大的随机数初始化会减慢优化的速度。
- 总而言之,将权重初始化为非常大的时候其实效果并不好,下面我们试试小一点的参数值。
2.5 抑梯度异常初始化
2.5.1 代码
def initialize_parameters_he(layers_dims):
"""
将模型的参数抑梯度异常初始化
参数:
layers_dims - 列表,模型的层数和对应每一层的节点的数量
返回
parameters - 包含了所有W和b的字典
W1 - 权重矩阵,维度为(layers_dims[1], layers_dims[0])
b1 - 偏置向量,维度为(layers_dims[1],1)
···
WL - 权重矩阵,维度为(layers_dims[L], layers_dims[L -1])
bL - 偏置向量,维度为(layers_dims[L],1)
"""
np.random.seed(3) # 指定随机种子
parameters = {}
L = len(layers_dims) #网络层数
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * np.sqrt(2/layers_dims[l-1]) # 10倍缩放
parameters["b" + str(l)] = np.zeros((layers_dims[l],1)) # b无所谓 可以还是初始化为0
#使用断言确保我的数据格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l],layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l],1))
return parameters
2.5.2 训练
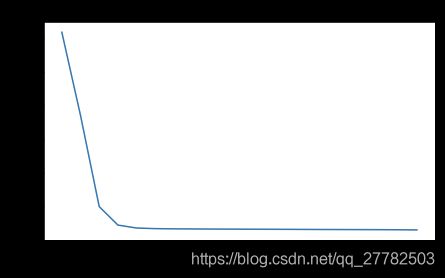
parameters = model(train_X,train_Y,initialization="he",is_polt=True)
parameters
第0次迭代,成本值为:0.8830537463419761
第1000次迭代,成本值为:0.6879825919728063
第2000次迭代,成本值为:0.6751286264523371
第3000次迭代,成本值为:0.6526117768893807
第4000次迭代,成本值为:0.6082958970572938
第5000次迭代,成本值为:0.5304944491717495
第6000次迭代,成本值为:0.4138645817071795
第7000次迭代,成本值为:0.31178034648444414
第8000次迭代,成本值为:0.2369621533032257
第9000次迭代,成本值为:0.18597287209206845
第10000次迭代,成本值为:0.1501555628037181
第11000次迭代,成本值为:0.12325079292273548
第12000次迭代,成本值为:0.09917746546525937
第13000次迭代,成本值为:0.08457055954024273
第14000次迭代,成本值为:0.07357895962677366
{'W1': array([[ 2.26930788, 1.0373042 ],
[ 0.66677708, -2.30154225],
[-0.29367404, -0.47621019],
[-0.56431372, -1.28550611],
[-0.0833954 , -0.37767036],
[-2.61667211, 0.58998578],
[ 1.17205304, 2.13928934],
[ 0.29920508, -0.71480482],
[-0.76036578, -1.72129222],
[ 1.6007726 , -1.84027265]]),
'W2': array([[-0.53142441, -0.09196943, 0.66462575, 0.10586273, -0.45785063,
-0.32575065, 0.26529788, -0.07193113, -0.34383407, -0.10287287],
[ 0.38133683, 0.77564511, -0.62439683, -0.41578462, -0.35406464,
-0.99607919, -0.29606634, 0.23084402, 0.42275344, -0.25953776],
[-0.72595532, 0.28920205, -0.15932913, -0.77955637, -0.26682983,
-0.26322741, -0.39081204, 0.01328842, -1.00545144, -0.11974675],
[ 0.12787355, 0.3388063 , 0.48200186, 0.48460282, 0.65301573,
-0.52408346, -0.02795833, -0.84266062, -0.31640932, -0.88706719],
[ 1.80657865, 1.69960454, 0.32553862, 1.54847526, -0.17913703,
2.2019285 , 1.6481392 , -1.96449025, 1.06244244, 2.12191174]]),
'W3': array([[-0.64865924, 0.99662957, -0.09771871, 0.9989112 , -5.3370528 ]]),
'b1': array([[-0.23394446],
[-0.25110623],
[-0.23443956],
[-0.52496578],
[ 0.03367351],
[ 0.09107832],
[-0.47678099],
[ 1.74920979],
[-0.43799719],
[-0.31092435]]),
'b2': array([[-0.04860647],
[ 1.03523628],
[ 0. ],
[-0.17145413],
[-2.23070032]]),
'b3': array([[2.8409238]])}
2.5.3 预测
print ("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print ("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
训练集:
Accuracy: 0.9933333333333333
测试集:
Accuracy: 0.96
卧槽 相当牛逼了,比上面的精度高了很多!
2.6 总结
-
不同的初始化方法可能导致性能最终不同
-
随机初始化有助于打破对称,使得不同隐藏层的单元可以学习到不同的参数。
-
初始化时,初始值不宜过大。
-
He初始化搭配ReLU激活函数常常可以得到不错的效果。
3 正则化
3.1 数据
import scipy.io as sio
def load_2D_dataset(is_plot=True):
data = sio.loadmat('datasets/data.mat')
train_X = data['X'].T
train_Y = data['y'].T
test_X = data['Xval'].T
test_Y = data['yval'].T
if is_plot:
plt.scatter(train_X[0, :], train_X[1, :], c=np.squeeze(train_Y), s=40, cmap=plt.cm.Spectral);
return train_X, train_Y, test_X, test_Y
train_X, train_Y, test_X, test_Y = load_2D_dataset(is_plot=True)
3.2 代码
由于引入正则化,损失函数的公式增加了一项,所以计算cost以及反向传播cost的代码需要变化
def compute_cost_with_regularization(A3,Y,parameters,lambd):
"""
实现公式2的L2正则化计算成本
参数:
A3 - 正向传播的输出结果,维度为(输出节点数量,训练/测试的数量)
Y - 标签向量,与数据一一对应,维度为(输出节点数量,训练/测试的数量)
parameters - 包含模型学习后的参数的字典
返回:
cost - 使用公式2计算出来的正则化损失的值
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = reg_utils.compute_cost(A3,Y)
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
cost = cross_entropy_cost + L2_regularization_cost
return cost
#当然,因为改变了成本函数,我们也必须改变向后传播的函数, 所有的梯度都必须根据这个新的成本值来计算。
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
实现我们添加了L2正则化的模型的后向传播。
参数:
X - 输入数据集,维度为(输入节点数量,数据集里面的数量)
Y - 标签,维度为(输出节点数量,数据集里面的数量)
cache - 来自forward_propagation()的cache输出
lambda - regularization超参数,实数
返回:
gradients - 一个包含了每个参数、激活值和预激活值变量的梯度的字典
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T) + ((lambd * W3) / m )
db3 = (1 / m) * np.sum(dZ3,axis=1,keepdims=True)
dA2 = np.dot(W3.T,dZ3)
dZ2 = np.multiply(dA2,np.int64(A2 > 0))
dW2 = (1 / m) * np.dot(dZ2,A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)
dA1 = np.dot(W2.T,dZ2)
dZ1 = np.multiply(dA1,np.int64(A1 > 0))
dW1 = (1 / m) * np.dot(dZ1,X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def model(X,Y,learning_rate=0.01,num_iterations=15000, lambd=0, print_cost=True,initialization="he",is_polt=True):
"""
实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
参数:
X - 输入的数据,维度为(2, 要训练/测试的数量)
Y - 标签,【0 | 1】,维度为(1,对应的是输入的数据的标签)
learning_rate - 学习速率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每迭代1000次打印一次
initialization - 字符串类型,初始化的类型【"zeros" | "random" | "he"】
is_polt - 是否绘制梯度下降的曲线图
lambd - 正则化参数
返回
parameters - 学习后的参数
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0],10,5,1]
#选择初始化参数的类型
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
else :
print("错误的初始化参数!程序退出")
exit
#开始学习
for i in range(0,num_iterations):
#前向传播
a3 , cache = init_utils.forward_propagation(X,parameters)
#计算成本
cost = init_utils.compute_loss(a3,Y)
#反向传播
grads = init_utils.backward_propagation(X,Y,cache)
#更新参数
parameters = init_utils.update_parameters(parameters,grads,learning_rate)
#记录成本
if i % 1000 == 0:
costs.append(cost)
#打印成本
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
#学习完毕,绘制成本曲线
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回学习完毕后的参数
return parameters
3.3 训练+预测
parameters = model(train_X, train_Y, lambd=0.7,is_polt=True)
print("使用正则化,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用正则化,测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.8182760536998407
第1000次迭代,成本值为:0.5702210539472338
第2000次迭代,成本值为:0.29835042886732865
第3000次迭代,成本值为:0.2432883931921556
第4000次迭代,成本值为:0.2344959083427152
第5000次迭代,成本值为:0.23264777653673396
第6000次迭代,成本值为:0.23204990707849468
第7000次迭代,成本值为:0.23171085396182836
第8000次迭代,成本值为:0.23137427703179395
第9000次迭代,成本值为:0.23116201993351987
第10000次迭代,成本值为:0.23096258775937067
第11000次迭代,成本值为:0.2307495523856153
第12000次迭代,成本值为:0.23054651748350388
第13000次迭代,成本值为:0.23032100457597718
第14000次迭代,成本值为:0.2300877112237079
使用正则化,训练集:
Accuracy: 0.919431279620853
使用正则化,测试集:
Accuracy: 0.915
正则化之后虽然准确率没有上面未正则化的高,但应该能有效避免过拟合的情况!
parameters = model(train_X, train_Y,is_polt=True,lambd=0.7,num_iterations=20000)
print("使用正则化,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用正则化,测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.8182760536998407
第1000次迭代,成本值为:0.5702210539472338
第2000次迭代,成本值为:0.29835042886732865
第3000次迭代,成本值为:0.2432883931921556
第4000次迭代,成本值为:0.2344959083427152
第5000次迭代,成本值为:0.23264777653673396
第6000次迭代,成本值为:0.23204990707849468
第7000次迭代,成本值为:0.23171085396182836
第8000次迭代,成本值为:0.23137427703179395
第9000次迭代,成本值为:0.23116201993351987
第10000次迭代,成本值为:0.23096258775937067
第11000次迭代,成本值为:0.2307495523856153
第12000次迭代,成本值为:0.23054651748350388
第13000次迭代,成本值为:0.23032100457597718
第14000次迭代,成本值为:0.2300877112237079
第15000次迭代,成本值为:0.22992655305094892
第16000次迭代,成本值为:0.2297797758224707
第17000次迭代,成本值为:0.22960314250832073
第18000次迭代,成本值为:0.22929240624776243
第19000次迭代,成本值为:0.2288307047561804
使用正则化,训练集:
Accuracy: 0.9241706161137441
使用正则化,测试集:
Accuracy: 0.915
4 dropout
需要修改代码的部分为前向传播和反向传播的过程,因为有些神经元失活了
4.1 代码
4.1.1前向
def forward_propagation_with_dropout(X,parameters,keep_prob=0.5):
"""
实现具有随机舍弃节点的前向传播。
LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
参数:
X - 输入数据集,维度为(2,示例数)
parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:
W1 - 权重矩阵,维度为(20,2)
b1 - 偏向量,维度为(20,1)
W2 - 权重矩阵,维度为(3,20)
b2 - 偏向量,维度为(3,1)
W3 - 权重矩阵,维度为(1,3)
b3 - 偏向量,维度为(1,1)
keep_prob - 随机删除的概率,实数
返回:
A3 - 最后的激活值,维度为(1,1),正向传播的输出
cache - 存储了一些用于计算反向传播的数值的元组
"""
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
#LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1,X) + b1
A1 = reg_utils.relu(Z1) # 激活后的值 但要失活一部分 所以有下面的代码
#下面的步骤1-4对应于上述的步骤1-4。
D1 = np.random.rand(A1.shape[0],A1.shape[1]) #步骤1:初始化矩阵D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob #步骤2:将D1的值转换为0或1(使用keep_prob作为阈值)
A1 = A1 * D1 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A1 = A1 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
"""
#不理解的同学运行一下下面代码就知道了。
import numpy as np
np.random.seed(1)
A1 = np.random.randn(1,3)
D1 = np.random.rand(A1.shape[0],A1.shape[1])
keep_prob=0.5
D1 = D1 < keep_prob
print(D1)
A1 = 0.01
A1 = A1 * D1
A1 = A1 / keep_prob
print(A1)
"""
Z2 = np.dot(W2,A1) + b2
A2 = reg_utils.relu(Z2)
#下面的步骤1-4对应于上述的步骤1-4。
D2 = np.random.rand(A2.shape[0],A2.shape[1]) #步骤1:初始化矩阵D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob #步骤2:将D2的值转换为0或1(使用keep_prob作为阈值)
A2 = A2 * D2 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A2 = A2 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
Z3 = np.dot(W3, A2) + b3
A3 = reg_utils.sigmoid(Z3) # 输出就1个神经元 所以不需要失活处理
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
4.1.2 反向
def backward_propagation_with_dropout(X,Y,cache,keep_prob):
"""
实现我们随机删除的模型的后向传播。
参数:
X - 输入数据集,维度为(2,示例数)
Y - 标签,维度为(输出节点数量,示例数量)
cache - 来自forward_propagation_with_dropout()的cache输出
keep_prob - 随机删除的概率,实数
返回:
gradients - 一个关于每个参数、激活值和预激活变量的梯度值的字典
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA2 = dA2 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA1 = dA1 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
4.1.3 主代码
def model(X,Y,learning_rate=0.01,num_iterations=15000,print_cost=True,initialization="he",is_polt=True, keep_prob=0.5):
"""
实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
参数:
X - 输入的数据,维度为(2, 要训练/测试的数量)
Y - 标签,【0 | 1】,维度为(1,对应的是输入的数据的标签)
learning_rate - 学习速率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每迭代1000次打印一次
initialization - 字符串类型,初始化的类型【"zeros" | "random" | "he"】
is_polt - 是否绘制梯度下降的曲线图
返回
parameters - 学习后的参数
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0],10,5,1]
#选择初始化参数的类型
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
else :
print("错误的初始化参数!程序退出")
exit
#开始学习
for i in range(0,num_iterations):
#前向传播
a3 , cache = forward_propagation_with_dropout(X,parameters,keep_prob=0.5)
#计算成本
cost = init_utils.compute_loss(a3,Y)
#反向传播
grads = backward_propagation_with_dropout(X,Y,cache,keep_prob)
#更新参数
parameters = init_utils.update_parameters(parameters,grads,learning_rate)
#记录成本
if i % 1000 == 0:
costs.append(cost)
#打印成本
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
#学习完毕,绘制成本曲线
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回学习完毕后的参数
return parameters
4.2 训练+预测
parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3,is_polt=True)
print("使用随机删除节点,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用随机删除节点,测试集:")
reg_utils.predictions_test = reg_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.8507860147818928
第1000次迭代,成本值为:0.3873714180471037
第2000次迭代,成本值为:0.3720394089743302
第3000次迭代,成本值为:0.35982370299095773
第4000次迭代,成本值为:0.3239536446466947
/Users/apple/Desktop/深度学习/课程2-week1/init_utils.py:50: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
/Users/apple/Desktop/深度学习/课程2-week1/init_utils.py:50: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
第5000次迭代,成本值为:0.26833101413187094
第6000次迭代,成本值为:0.2590069112583366
第7000次迭代,成本值为:0.2542389928282903
第8000次迭代,成本值为:0.25224163263185556
第9000次迭代,成本值为:0.25109259309986964
第10000次迭代,成本值为:0.2503088273978559
第11000次迭代,成本值为:0.2497141227182644
第12000次迭代,成本值为:0.2494909360725536
第13000次迭代,成本值为:0.24923710314189443
第14000次迭代,成本值为:0.2489525908753509
使用随机删除节点,训练集:
Accuracy: 0.9241706161137441
使用随机删除节点,测试集:
Accuracy: 0.91
用dropout运行模型(keep_prob = 0.86)跑一波。这意味着在每次迭代中,程序都可以24%的概率关闭第1层和第2层的每个神经元。
5 梯度校验
本质上做的事情是:看dw db和直接根据导数公式近似的值是否差异很大 如果很大 可能出现了bug
5.1 一维情形
5.1.1 前向传播
def forward_propagation(x,theta):
"""
实现图中呈现的线性前向传播(计算J)(J(theta)= theta * x)
参数:
x - 一个实值输入
theta - 参数,也是一个实数
返回:
J - 函数J的值,用公式J(theta)= theta * x计算
"""
J = np.dot(theta,x)
return J
5.1.2 反向传播
def backward_propagation(x,theta):
"""
计算J相对于θ的导数。
参数:
x - 一个实值输入
theta - 参数,也是一个实数
返回:
dtheta - 相对于θ的成本梯度
"""
dtheta = x
return dtheta
5.1.3 梯度校验
def gradient_check(x,theta,epsilon=1e-7):
"""
实现图中的反向传播。
参数:
x - 一个实值输入
theta - 参数,也是一个实数
epsilon - 使用公式(3)计算输入的微小偏移以计算近似梯度
返回:
近似梯度和后向传播梯度之间的差异
"""
#使用公式(3)的左侧计算gradapprox。
thetaplus = theta + epsilon # Step 1
thetaminus = theta - epsilon # Step 2
J_plus = forward_propagation(x, thetaplus) # Step 3
J_minus = forward_propagation(x, thetaminus) # Step 4
gradapprox = (J_plus - J_minus) / (2 * epsilon) # Step 5
#检查gradapprox是否足够接近backward_propagation()的输出
grad = backward_propagation(x, theta)
numerator = np.linalg.norm(grad - gradapprox) # Step 1' 计算L2范数
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference
5.1.4 测试
#测试gradient_check
print("-----------------测试gradient_check-----------------")
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
-----------------测试gradient_check-----------------
梯度检查:梯度正常!
difference = 2.919335883291695e-10
5.2 高维情形
5.2.1 前向传播+反向传播
def forward_propagation_n(X,Y,parameters):
"""
实现图中的前向传播(并计算成本)。
参数:
X - 训练集为m个例子
Y - m个示例的标签
parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:
W1 - 权重矩阵,维度为(5,4)
b1 - 偏向量,维度为(5,1)
W2 - 权重矩阵,维度为(3,5)
b2 - 偏向量,维度为(3,1)
W3 - 权重矩阵,维度为(1,3)
b3 - 偏向量,维度为(1,1)
返回:
cost - 成本函数(logistic)
"""
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1,X) + b1
A1 = gc_utils.relu(Z1)
Z2 = np.dot(W2,A1) + b2
A2 = gc_utils.relu(Z2)
Z3 = np.dot(W3,A2) + b3
A3 = gc_utils.sigmoid(Z3)
#计算成本
logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = (1 / m) * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
def backward_propagation_n(X,Y,cache):
"""
实现图中所示的反向传播。
参数:
X - 输入数据点(输入节点数量,1)
Y - 标签
cache - 来自forward_propagation_n()的cache输出
返回:
gradients - 一个字典,其中包含与每个参数、激活和激活前变量相关的成本梯度。
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1. / m) * np.dot(dZ3,A2.T)
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
#dW2 = 1. / m * np.dot(dZ2, A1.T) * 2 # Should not multiply by 2
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
#db1 = 4. / m * np.sum(dZ1, axis=1, keepdims=True) # Should not multiply by 4
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
5.2.2 梯度校验
def gradient_check_n(parameters,gradients,X,Y,epsilon=1e-7):
"""
检查backward_propagation_n是否正确计算forward_propagation_n输出的成本梯度
参数:
parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:
grad_output_propagation_n的输出包含与参数相关的成本梯度。
x - 输入数据点,维度为(输入节点数量,1)
y - 标签
epsilon - 计算输入的微小偏移以计算近似梯度
返回:
difference - 近似梯度和后向传播梯度之间的差异
"""
#初始化参数
parameters_values , keys = gc_utils.dictionary_to_vector(parameters) #keys用不到
grad = gc_utils.gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters,1))
J_minus = np.zeros((num_parameters,1))
gradapprox = np.zeros((num_parameters,1))
#计算gradapprox
for i in range(num_parameters):
#计算J_plus [i]。输入:“parameters_values,epsilon”。输出=“J_plus [i]”
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaplus)) # Step 3 ,cache用不到
#计算J_minus [i]。输入:“parameters_values,epsilon”。输出=“J_minus [i]”。
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaminus))# Step 3 ,cache用不到
#计算gradapprox[i]
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
#通过计算差异比较gradapprox和后向传播梯度。
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference
参考
- https://blog.csdn.net/u013733326/article/details/79847918#commentBox