基于前馈神经网络(SLFN)的极限学习机-遗传算法相结合
文章目录
-
-
- 一、极限学习机
-
- 1.1 概要
- 1.2 优点
- 1.3 不足
- 1.4 改进
- 二、前馈神经网络结构
-
- 2.1 构成
- 2.2 变量解释
- 2.3 β 求解
- 三、遗传算法(GA)
-
- 3.1 概要
- 3.2 遗传算法流程
- 3.3 执行过程
-
一、极限学习机
资料参考:
- https://www.jiqizhixin.com/graph/technologies/d6f12c89-0d07-46ac-89a0-af978df2ce8e
- https://blog.csdn.net/tianguiyuyu/article/details/80014820
1.1 概要
极限学习机是基于单隐含层的前馈神经网络(SLFN)的新算法,相对于传统的前馈神经网络训练速度慢,容易陷入局部极小值 ,学习率的选择敏感等缺点,ELM 算法随机产生输入层与隐含层的连接权值及隐含层神经元的阈值,且在训练的过程中无需调整,只需要设置隐含层神经元的个数,便可以获得唯一的最优解。
1.2 优点
- 学习速度快
- 泛化性能好
1.3 不足
- 输入权重与隐含层阈值随机确定,行为分析结果随机性强,可靠程度。
1.4 改进
高适应度的遗传算法确定极限学习机算法的输入权值和阈值。
二、前馈神经网络结构
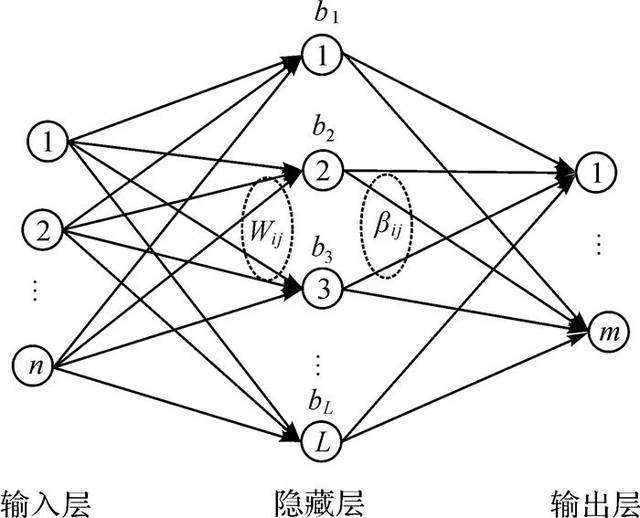
2.1 构成
- 由输入层、隐含层、和输出层组成
- 输入层与隐含层,隐含层与输出层神经元间全连接
- 输入层有n个神经单元,对应n个输入变量;
- 隐含层有L个神经元;
- 输出层有m个神经元,对应m个输出变量。
2.2 变量解释
- 输入层与隐含层间的连接权值
W
W = [ w 11 w 12 ⋯ w 1 n w 21 w 22 ⋯ w 2 n ⋮ ⋮ ⋱ ⋮ w l 1 w l 2 ⋯ w l n ] l × n W = \begin{bmatrix} {w_{11}}&{w_{12}}&{\cdots}&{w_{1n}}\\ {w_{21}}&{w_{22}}&{\cdots}&{w_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {w_{l1}}&{w_{l2}}&{\cdots}&{w_{ln}}\\ \end{bmatrix}_{l \times n} W=⎣⎢⎢⎢⎡w11w21⋮wl1w12w22⋮wl2⋯⋯⋱⋯w1nw2n⋮wln⎦⎥⎥⎥⎤l×n
解 释 : w j i 表 示 输 入 层 第 i 个 神 经 元 与 隐 含 层 第 j 个 神 经 元 的 连 接 权 值 解释:w_{ji}表示输入层第i个神经元与隐含层第j个神经元的连接权值 解释:wji表示输入层第i个神经元与隐含层第j个神经元的连接权值
- 隐含层与输出层间的连接权值
β
β = [ β 11 β 12 ⋯ β 1 n β 21 β 22 ⋯ β 2 n ⋮ ⋮ ⋱ ⋮ β l 1 β l 2 ⋯ β l n ] l × m β = \begin{bmatrix} {β_{11}}&{β_{12}}&{\cdots}&{β_{1n}}\\ {β_{21}}&{β_{22}}&{\cdots}&{β_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {β_{l1}}&{β_{l2}}&{\cdots}&{β_{ln}}\\ \end{bmatrix}_{l \times m} β=⎣⎢⎢⎢⎡β11β21⋮βl1β12β22⋮βl2⋯⋯⋱⋯β1nβ2n⋮βln⎦⎥⎥⎥⎤l×m
解 释 : β j k 表 示 隐 含 层 第 j 个 神 经 元 与 输 出 层 第 k 个 神 经 元 的 连 接 权 值 解释:β_{jk}表示隐含层第j个神经元与输出层第k个神经元的连接权值 解释:βjk表示隐含层第j个神经元与输出层第k个神经元的连接权值
- 隐含层神经元的阈值
b
b = [ b 1 b 2 ⋮ b l ] l × 1 b = \begin{bmatrix} {b_{1}}\\ {b_{2}}\\ {\vdots}\\ {b_{l}}\\ \end{bmatrix}_{l \times 1} b=⎣⎢⎢⎢⎡b1b2⋮bl⎦⎥⎥⎥⎤l×1
-
Q 个样本训练集输入矩阵 X 和输出矩阵
YX = [ x 11 x 12 ⋯ x 1 Q x 21 x 22 ⋯ x 2 Q ⋮ ⋮ ⋮ ⋮ x n 1 x n 2 ⋯ x n Q ] n × Q Y = [ y 11 y 12 ⋯ y 1 Q y 21 y 22 ⋯ y 2 Q ⋮ ⋮ ⋮ ⋮ y m 1 y m 2 ⋯ y m Q ] m × Q X = \begin{bmatrix} {x_{11}}&{x_{12}}&{\cdots}&{x_{1Q}}\\ {x_{21}}&{x_{22}}&{\cdots}&{x_{2Q}}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ {x_{n1}}&{x_{n2}}&{\cdots}&{x_{nQ}}\\ \end{bmatrix}_{n \times Q} Y = \begin{bmatrix} {y_{11}}&{y_{12}}&{\cdots}&{y_{1Q}}\\ {y_{21}}&{y_{22}}&{\cdots}&{y_{2Q}}\\ {\vdots}&{\vdots}&{\vdots}&{\vdots}\\ {y_{m1}}&{y_{m2}}&{\cdots}&{y_{mQ}}\\ \end{bmatrix}_{m \times Q} X=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋮⋯x1Qx2Q⋮xnQ⎦⎥⎥⎥⎤n×QY=⎣⎢⎢⎢⎡y11y21⋮ym1y12y22⋮ym2⋯⋯⋮⋯y1Qy2Q⋮ymQ⎦⎥⎥⎥⎤m×Q
- 网络训练模型(隐含层神经元激活函数为
g(x))
∑ i = 1 l β i g ( w i ⋅ x i + b i ) = o j , j = 1 , 2 , . . . , M \sum_{i=1}^{l}\beta _{i}g(w_i\cdot x_i+b_i) = o_j, j=1,2,...,M i=1∑lβig(wi⋅xi+bi)=oj,j=1,2,...,M
式中,w_i 表示输入层节点与第 i 个隐层节点的输入权值向量,\beta_i 表示连接第 i 个隐层节点与输出层节点的输出权值向量;o_j 表示网络输出值。
w i = [ w i 1 w i 2 ⋯ w i n ] ; x j = [ x 1 j x 2 j ⋯ x n j ] T w_i = \begin{bmatrix} {w_{i1}}&{w_{i2}}&{\cdots}&{w_{in}} \end{bmatrix} ; x_j = \begin{bmatrix} {x_{1j}}&{x_{2j}}&{\cdots}&{x_{nj}} \end{bmatrix}^T wi=[wi1wi2⋯win];xj=[x1jx2j⋯xnj]T
- H 神经网络的隐含层输出矩阵
H ( w 1 , . . . , w l , b 1 , . . . , b l , x 1 , . . . , x Q ) = [ g ( w 1 x 1 + b 1 ) ⋯ g ( w l x 1 + b l ) ⋮ ⋮ g ( w 1 x Q + b 1 ) ⋯ g ( w l x Q + b l ) ] Q × l H(w_1,...,w_l, b_1,...,b_l, x_1,...,x_Q)={\begin{bmatrix} g(w_1x_1+b_1) & \cdots & g(w_lx_1+b_l)\\ \vdots & & \vdots \\ g(w_1x_Q+b_1) & \cdots & g(w_lx_Q+b_l) \end{bmatrix}}_{Q \times l} H(w1,...,wl,b1,...,bl,x1,...,xQ)=⎣⎢⎡g(w1x1+b1)⋮g(w1xQ+b1)⋯⋯g(wlx1+bl)⋮g(wlxQ+bl)⎦⎥⎤Q×l
2.3 β 求解
当激活函数 g(x)无限可微是,SLFN 的参数不需要全部进行调整,w 和 b 在训练之前可以随机的选择,且在训练过程中保持不变。隐含层和输出层的连接权值 β 可以通过求解以下方程组的最小二乘解获得:
三、遗传算法(GA)
3.1 概要
遗传算法是 Holland 教授与 1975 年提出的一种模拟自然界遗传机制和生物进化论的搜索全局最优解算法。GA 把搜索空间映射为遗传空间,把可能的解编码成一个向量----染色体,向量的每一个元素称之为基因,同步不断计算各个染色体的适应值,选择最好的染色体获得最优解。
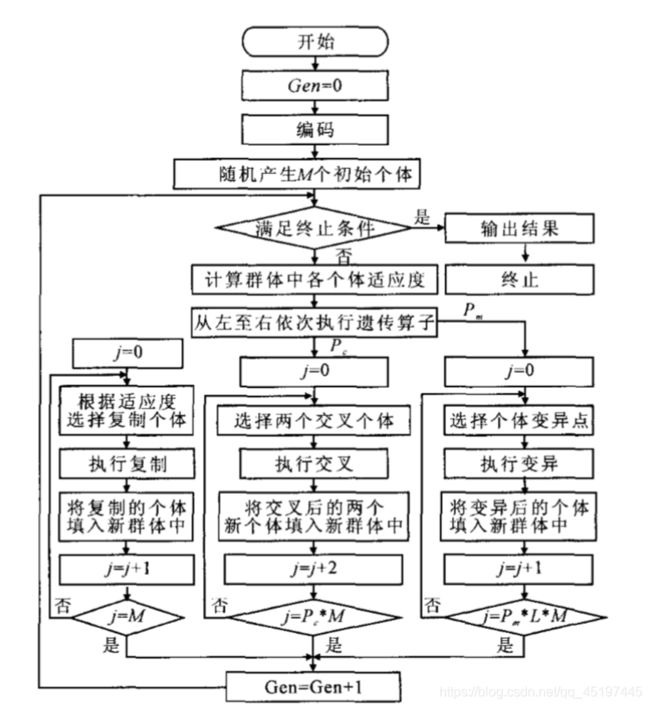
3.2 遗传算法流程
3.3 执行过程
(1)初始化。确定种群规模 M M M,随机生成 M M M 个染色体作为初始种群 Y ( 0 ) Y(0) Y(0)、交叉概率 P P P、变异概率 P m P_m Pm、终止进化代数 N N N。
(2)计算个体适应度。计算第 t 代 种群 Y(t)中每个染色体的适应度。设种群为 f ( y ) f(y) f(y), y ∈ M y∈ M y∈M,其中 M = { y 1 , . . . . , y m } M =\{y_1,.... ,y_m\} M={y1,....,ym},, y i = { x 1 , . . . . . , x m } y_i = \{x_1 , ..... , x_m\} yi={x1,.....,xm}, 每个染色体含 m 个基因 , 则
f ( y ) = [ y 1 y 2 ⋮ y M ] = [ x 11 ⋯ x 1 m ⋮ ⋯ ⋮ y M ⋯ x M m ] f(y) = \begin{bmatrix} {y_{1}}\\ {y_{2}}\\ {\vdots}\\ {y_{M}}\\ \end{bmatrix}=\begin{bmatrix} {x_{11}}&{\cdots}&{x_{1m}}\\ {\vdots}&{\cdots}&{\vdots}\\ {y_{M}}&{\cdots}&{x_{Mm}}\\ \end{bmatrix} f(y)=⎣⎢⎢⎢⎡y1y2⋮yM⎦⎥⎥⎥⎤=⎣⎢⎡x11⋮yM⋯⋯⋯x1m⋮xMm⎦⎥⎤
适应度函数为 f i t ( y ) fit(y) fit(y), y ∈ { y 1 , . . . , y m } y∈\{y_1 ,... ,y_m\} y∈{y1,...,ym} ,求取 f i t ( y ) fit(y) fit(y) 函数时,假设为优化神经网络,则
f i t ( y i ) = 1 / n ∑ j = 1 n ( O j − Y j ) 2 fit(y_i)= 1/n\sum_{j=1}^{n}(O_j - Yj)^2 fit(yi)=1/nj=1∑n(Oj−Yj)2
其中: O j O_j Oj 为第 j 个预测输出值; T j T_j Tj 为实际输出值;n 为输入数据总数。
(3)进化。选择(母体):从 Y ( t ) Y(t) Y(t) 中运用选择算子选择出L对母体L≥M;交叉:随机选择 L 2 \frac{L}2 2L 对染色体(双亲染色体),当其中一个染色体概率小于 P c P_{c} Pc 时,随机制定一点或者多点进行交叉,可以得到新的染色体(子辈染色体),最后形成 L L L 个中间个体;变异:对 L L L 个中间个体分别依概率 P m P_{m} Pm 执行变异,形成 M M M 个候选个体。
(4)选择子代。从上述种群中形成的 L L L 个候选个体中选择适应度高的 M M M 个染色体,形成新一代种群 Y ( t + 1 ) Y(t+1) Y(t+1) ,选择方法是适应度比例法(轮转法)。
某染色体被选择的概率为: P c P_{c} Pc:
p c = f i t ( y i ) ∑ f i t ( y i ) p_{c} = \frac{fit(y_{i})}{\sum_{}fit(y_{i})} pc=∑fit(yi)fit(yi)
y i y_{i} yi 为种群中第 i 个染色体, f i t ( y i ) fit(y_{i}) fit(yi) 是第 i 个染色体的适应度值, ∑ f i t ( y i ) \sum{fit(y_{i})} ∑fit(yi) 是种群所有染色体适应度值之和。
具体步骤:① 计算各染色体适应度值;② 累计所有染色体适应度值,记录中间累加值 S − m i d S-mid S−mid 和最后累加值 s u m = ∑ f i t ( y i ) sum = \sum{fit(y_{i})} sum=∑fit(yi);③ 产生一个随机数 N,0 < N < sum;④ 选择对应重甲累加值 S − m i d S-mid S−mid 的第一个染色体进入交换集;⑤ 重复 ③ 和 ④ 知道获得足够的染色体。
(5)终止进化。当达到进化代数 N 时,终止进化,选择出第 N 代中适应度最高的染色体作为最优解。
t a r g e t v a l u e = m a x f i t ( y i ) targetvalue = max{fit(y_{i})} targetvalue=maxfit(yi)