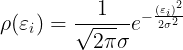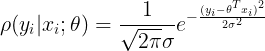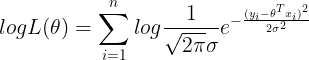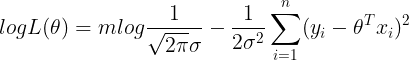机器学习——线性回归数学推导
文章目录
- 线性回归数学推导
-
- 基础知识
- 线性回归的计算
-
- 利用矩阵知识对线性公式进行整合
- 误差项的分析
- 似然函数的理解
- 矩阵求偏导
- 线性回归的最终求解
- 实验
-
- 1 二维直线实验
- 2 三维平面实验
- 3 利用最小二乘法求解
- 总结
线性回归数学推导
基础知识
线性回归的公式:
![]()
可以借助下面的表格来理解:
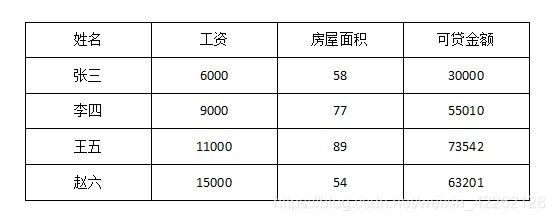
对应于线性回归方程,工资和房屋面积是线性回归模型中的x,可贷款金额是y。对于不同的工资和房屋面积对可贷款金额的影响程度是不一样的,每一个特征的参数就是上述模型中的a值。b是一个误差项,例如有两个人工资和房屋面积是一样的,但是最终的可贷款金额并不一定相同,这是因为在计算中存在一定的误差,受影响与一些微小的特征,这里就将对结果影响微小的误差统一归一为一个误差值。而线性回归最终要做的就是根据不同的影响求出最终的计算结果,而其中最重要的就是区求a值。
这就涉及到有监督的算法使用。有监督就是先给定一批x、y数据,推导出一个比较合适的a,这样再给出一个x值就可以根据这个a值求出最终的y,其中包含了训练和测试两部分。
线性回归的计算
利用矩阵知识对线性公式进行整合
那么该如何求解a呢?
在上述模型中,有工资和房屋面积两个特征,可贷款金额为目标函数值。根据线性函数可以得到以下公式:
![]()
若假设有n个特征,就将上式通用化为:
在机器学习中,需要将这个数学公式转换为矩阵的形式。由矩阵的乘法可以得到:
将权重参数和特征参数,都看成是1行n列的矩阵,就可以把多项式求和的式子转换成矩阵的乘法表达式,就可以将多项式求和化简为:
![]()
这就是机器学习所认可的一个矩阵的公式。
这个就是第一步,利用矩阵知识对线性公式进行整合。
误差项的分析
在上述的线性回归函数中,还需要求解b。也就是通常所说的偏移量或误差项。
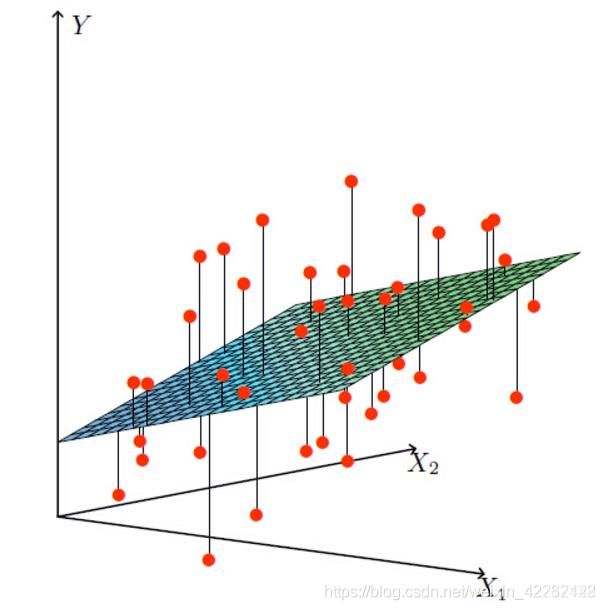
在这个图中,横坐标x1,x2分别代表着两个特征(工资、房屋面积),纵坐标y代表目标(可贷款的额度),平面是线性回归公式推导出来的目标平面,其中红点表示实际的目标值(每个人可贷款的额度)。红点和平面之间的误差就是所要求的的误差项。由此,之前所述的求解公式就转变为:
![]()
这样就得到了一个机器学习所认可的完整的线性回归公式。
根据实际情况,我们假设认为这个误差项是满足以下几个条件的:误差ε是独立并且具有相同的分布,并且服从均值为0方差为θ^2的高斯分布。
- 独立:张三和李四一起使用这款产品,可贷款额度互不影响;
- 同分布:张三和李四使用的是同一款贷款产品;
- 高斯分布:绝大多数情况下,在一个空间内浮动不大。
注:为什么一定是高斯分布呢?因为想要使用线性回归,在预先拿到一系列数据后,判断这些数据是符合高斯分布的,这也就是先前假设的误差项满足的条件之一。
似然函数的理解
在上一步的结论中,已经知道误差项ε是符合高斯分布的,所以误差项的概率密度函数就是下面这个式子(均值为0):
再把误差值代入到这个式子中,就得到:
对于误差项来说,肯定是越小越好。那么,考虑什么样的参数和特征的组合可以使误差项最小,这就需要引入似然函数。似然函数的作用就是要根据样本来求什么样的参数和特征的组合能够使结果最接近真实值,越接近真实值则误差越小。
似然估计函数为:
求解最大似然估计,利用对数将多个数相乘转化为多个数相加的形式(因为似然函数是越大越好,似然函数的值和对数似然函数的值是成正比的,对值求对数并不会影响到最后求极限的值,所以可以进行对数处理)。
整理后得到下面这个式子:
将这个式子拆解化简后,得到的最终表达式形式为:
因为我们要求似然估计的极大值,那么在上述式子中,第一项是一个定值,就只需要求第二项的极小值,即最小二乘法。
矩阵求偏导
现在对上述式子的第二项做一个转化,将数学公式转换为矩阵公式:
接下来对这个式子求偏导,然后取驻点,可以得到最小二乘法中的一个最小值:
这里需要用到矩阵求偏导的公式,可以参考这篇文章来学习:机器学习中的线性代数之矩阵求导
所以我们就可以根据这些公式将偏导求出:
线性回归的最终求解
令上式等于0来求驻点,最后解得的θ的值为:
![]()
在这个式子中,x和y都是已知的,那么就得到了一个最终的参数值,即y=ax+b中的a。有了这个值,代入新的x值就可以得到目标y值。
这就是线性回归的数学推导过程。
实验
1 二维直线实验
这个例子是根据房屋面积、房屋价格的历史数据,建立线性回归模型。然后根据给出的房屋面积来预测房屋价格。实验代码如下:
import pandas as pd
from io import StringIO
from sklearn import linear_model
import matplotlib.pyplot as plt
csv_data = 'square_feet,price\n 150, 6450\n 200, 7450\n 250, 8450\n 300, 9450\n 350, 11450\n 400, 15450\n 600, 18450\n'
df = pd.read_csv(StringIO(csv_data))
print(df)
regr = linear_model.LinearRegression()
regr.fit(df['square_feet'].values.reshape(-1, 1), df['price'])
a, b = regr.coef_, regr.intercept_
area = 238.5
print(a * area + b)
print(regr.predict([[area]]))
plt.scatter(df['square_feet'], df['price'], color = 'blue')
plt.plot(df['square_feet'], regr.predict(df['square_feet'].values.reshape(-1, 1)), color = 'red', linewidth = 4)
plt.show()
运行该程序,得到的预测房价和线性回归模型如下图所示:

上述代码先导入历史数据(csv文件),并围绕数据建立线性回归模型,拟合后得到直线的斜率和截距。给出待预测面积238.5,求得预测价格8635.027。由上图可以看出,实际的数据点围绕回归直线上下波动。
2 三维平面实验
在这个实验中,已知线性方程为z=ax+by+c表示一空间平面,利用一组虚拟数据绘制平面。实验代码如下:
import numpy as np
from sklearn import linear_model
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
xx, yy = np.meshgrid(np.linspace(0, 10, 10), np.linspace(0, 100, 10))
zz = 1.0 * xx + 3.5 * yy + np.random.randint(0, 100, (10, 10))
X, Z = np.column_stack((xx.flatten(), yy.flatten())), zz.flatten()
regr = linear_model.LinearRegression()
regr.fit(X, Z)
a, b = regr.coef_, regr.intercept_
x = np.array([[5.8, 78.3]])
print(np.sum(a * x) + b)
print(regr.predict(x))
fig = plt.figure()
ax = fig.gca(projection = '3d')
ax.scatter(xx, yy, zz)
ax.plot_wireframe(xx, yy, regr.predict(X).reshape(10, 10))
ax.plot_surface(xx, yy, regr.predict(X).reshape(10, 10), alpha = 0.3)
运行程序,得到输出值和求得的三维平面如下图所示:

上述代码根据构建的特征、值的形式建立线性回归模型并求得平面的斜率和截距。根据线性方程计算待预测特征x对应的z值为330.13516364。由上图可见,通过一组虚拟数围绕拟合的线性回归平面上下波动。
3 利用最小二乘法求解
import numpy as np
import matplotlib.pyplot as plt
def fun2ploy(x, n):
lens = len(x)
X = np.ones([1, lens])
for i in range(1, n):
X = np.vstack((X, np.power(x, i)))
return X
def leastseq_byploy(x, y, ploy_dim):
plt.scatter(x, y, color = 'r', marker = 'o', s =50)
X = fun2ploy(x, ploy_dim)
Xt = X.transpose()
XXt = X.dot(Xt)
XXtInv = np.linalg.inv(XXt)
XXtInvX = XXtInv.dot(X)
coef = XXtInvX.dot(y.T)
y_est = Xt.dot(coef)
return y_est, coef
def fit_fun(x):
return np.sin(x)
if __name__ == '__main__':
data_num = 100
ploy_dim = 10
noise_scale = 0.2
x = np.array(np.linspace(-2 * np.pi, 2 * np.pi, data_num))
y = fit_fun(x) + noise_scale * np.random.rand(1, data_num)
[y_est, coef] = leastseq_byploy(x, y, ploy_dim)
org_data = plt.scatter(x, y, color = 'r', marker = 'o', s =50)
est_data = plt.plot(x, y_est, color = 'g', linewidth = 3)
plt.xlabel("X")
plt.ylabel("Y")
plt.title("Fit function with leastseq method")
plt.legend(["Noise data", "Fit function"])
plt.show()
运行程序得到的最小二乘拟合效果如图所示:

最小二乘法是一种数学优化算法。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以通过样本求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。由上图可见,绿色实线即为实际值与拟合函数之间的差距,在算法实现过程中,尽量使它的平方和最小,达到了较好的拟合效果。
总结
回归是一种监督学习算法,其目标是通过对训练样本的学习,得到从样本特征到样本目标的映射,并且目标和特征之间存在线性相关关系。
对于线性回归算法,从训练数据集中学习到线性回归方程模型,求出要求误差值尽可能的小的线性回归方程。
其算法过程如下:
- 利用矩阵的知识对线性公式进行整合
- 误差项的分析
- 似然函数的理解
- 矩阵求偏导
- 线性回归的最终求解