2.深度学习模型使用：（卷积层，池化层，全连接层）

---

前言

网络模型在算法中比较常用，对于大部分的网络结构模型都包含以下各层，本文主要是来介绍各层的特点以及使用，对于结合实际的需求搭建模型，可以参考我的其他博客。

---

一、卷积层

卷积就是使用输入矩阵与卷积核进行卷积运算，通过卷积计算后的结果就是目标的特征信息。计算如下：
在上述5 * 5的输入矩阵与3 * 3的kernel进行卷积运算，得到的是3 * 3的目标矩阵。
可以明显的知道输出矩阵
w = img.shape[0]-kernel.shape[0]+1。
h = img.shape[1]-kernel.shape[1]+1。
矩阵的特征信息减少了，如果要维持5 * 5的维度，需要设置一个padding=1，进行0扩充。

pytorch给定的卷积输入形状与输出形状关系如下：
根据上述公式，对于一个卷积核大小为k，如果要保持输入输出的维度不变，需要设置paddi值为：k // 2。
pytorch中给出的卷积层函数包含的参数较多，因为大部分都有默认值，这里只举出常用的一些：nn.Conv2d(in_channels, out_channels, kernel_size stride, padding)
in_channels:输入的维度
out_channels:输出的维度
kernel_size:卷积核大小
stride:卷积核每步移动的距离，默认是1
padding:边缘填充，默认是0
在卷积层中使用多通道输入，单通道输出如下所示：

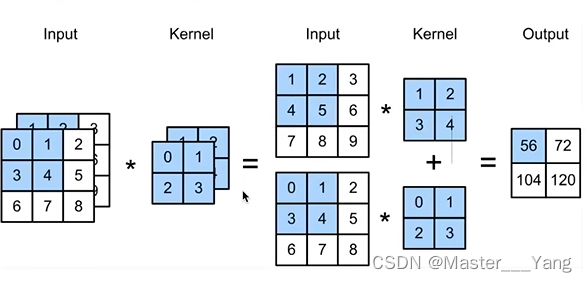
对于多通道输出，图像的输出输出特征信息如下所示：

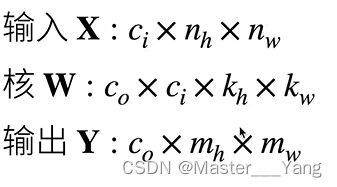
二、池化层

池化层是降低数据特征的维度,在一定程度上防止数据的过拟合，同时缓解卷积层对于位置的敏感性。在这层中通常使用较多的是MaxPool2d和AvgPool2d,区别在于使用卷积核进行运算时，是采取最大值还是平均值。以MaxPool2d为例，在下述矩阵中采用大小为二的卷积核，输出如下。若采用平均池化层，则是对每一个卷积核内的内容取平均值。

上述卷积核移动的步长是默认值None，因此输出矩阵大小均缩小一半。

nn.MaxPool2d(kernel_size=3)

pytorch中给定的池化层函数中，卷积核尺寸是没有默认值的，其余的均用。

• stride:卷积核移动的步长，默认为None（即卷积核大小）
• padding：输入矩阵进行填充，默认为0
• ceil_mode: 是否过滤掉那些不满足卷积核大小的区域，默认为False
• dilation：卷积核膨胀尺寸，默认值为1

卷积核计算公式为：
膨胀的卷积核尺寸 = 膨胀系数 * (原始卷积核尺寸 - 1) + 1
举如下例子：卷积核大小为3，stride大小为3，ceil_mode为True,图解如下：

model = nn.MaxPool2d(kernel_size=3,stride=None,ceil_mode=True)
input = torch.Tensor([[[5, 1, 2, 5],
                       [3, 2, 1, 8],
                       [2, 6, 1, 1],
                       [6, 1, 4, 7]]])
output = model(input)
print(output)

输出：

tensor([[[6., 8.],
         [6., 7.]]])

---

三、线性层（全连接层）

3.1全连接

全连接层基本上用来作为模型的最后一层，是将每个神经元与所用前后的神经元进行连接，得到图像的特征信息输出。如下图所示，判断一张图片是否是猫，建立了2层全连接层计算，得到猫的特征信息输出。在建立全连接层时，有时会出现过拟合现象，因此常常会使用Drop来减低数据的拟合度。

pytorch中给出了几个全连接计算函数，在通常使用多的是线性转化：

torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)

• in_features: 输入维度。 out_features: 输出维度

3.2激活函数

在卷积网络中，不使用激活函数，模型就是输入的线性组合，无论添加多少层模型，结果无非还是矩阵相乘，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大。
常用的非线性激活函数有：sigmoid、tanh、relu函数。这个部分主要介绍一下主要的激活函数的特征。
在介绍之前先提两个重要的概念梯度消失、梯度爆炸：

梯度消失：

指的是导函数的图像过于平直，求导后的值越来越接近于0，根据梯度更新公式可以知道，参数的下降速度是非常慢的，从而导致收敛速度慢，训练时间无限延长。

梯度爆炸：

梯度爆炸就是由于初始化权值过大，前面层会比后面层变化的更快，就会导致权值越来越大，梯度爆炸的现象就发生了。

在深层网络或循环神经网络中，误差梯度可在更新中累积，变成非常大的梯度，然后导致网络权重的大幅更新，并因此使网络变得不稳定。在极端情况下，权重的值变得非常大，以至于溢出，导致 NaN 值。
网络层之间的梯度（值大于 1.0）重复相乘导致的指数级增长会产生梯度爆炸。

1.sigmoid

sigmoid

显然其导数dy=y*(1-y)。函数的图像如下所示：

特点
它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.
缺点

• 输出值不以零为中心。
• 深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。
• 其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

2.tanh

导数dy = 1-tanh(x)*tanh(x) ,函数图像为：

特点：
解决了sigmoid函数输出不关于0点对称，根据导函数可知，导函数易求，图像平滑。
缺点：
和sigmoid函数一样，导函数小于1易发生梯度消失，同时函数包含指数运算，时间花费较大。

3.Relu

relu函数是现在神经网络通常使用的一个激活函数，表达式为f(x)=max(0,x)。因为导数形式比较简单就不做图像描绘
特点：
计算简单，没有指数运算等，解决了梯度消失的问题（在正区间内），参数的收敛速度也很快。
缺点：

• 和sigmoid函数一样，没有解决zero-centered问题。
• Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

3.3Drop层

Dropout通常使用在全连接层，一般来说，我们在可能发生过拟合的情况下才会使用dropout等正则化技术。那什么时候可能会发生呢？比如神经网络过深，或训练时间过长，或没有足够多的数据时。那为什么dropout能有效防止过拟合呢？可以理解为，我们每次训练迭代时，随机选择一批单元不参与训练，这使得每个单元不会依赖于特定的前缀单元，因此具有一定的独立性；同样可以看成我们拿同样的数据在训练不同的网络，每个网络都有可能过拟合，但迭代多次后，这种过拟合会被抵消掉。

在现在的神经网络模型下，Dropout使用的也越来越少，也逐渐被（Batch Normal）所取代，因为Dropout主要作用于FC层，而很多检测模型不使用FC，其次其正则化的能力有限，在过多的忽略神经元，会导致模型的收敛步长加大， 而且模型的准确性降低。
对于BN和Dropout比较可以参考以下博客：

https://blog.csdn.net/m0_37870649/article/details/82025238

3.4Bath_Normal层

BN是将数据进行归一化处理（均值为0，方差为1），如果不做归一化，使用mini-batch梯度下降法训练的时候，每批训练数据的分布不相同，那么网络就要在每次迭代的时候去适应不同的分布，这样会大大降低网络的训练速度。
根据论文中，BN是做了一下这些步骤（xi是输入，yi是输出）：

Pytorch中的BN操作为：

nn.BatchNorm2d(num_features, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)

• num_features，输入数据的通道数，归一化时需要的均值和方差是在每个通道中计算的
• eps，用来防止归一化时除以0
• momentum，滑动平均的参数，用来计算running_mean和running_var
• affine，是否进行仿射变换，即缩放操作
• track_running_stats，是否记录训练阶段的均值和方差，即running_mean和running_var