web3：同态加密

web3相关学习一并收录至该博客：web3学习博客目录大全

同态加密概念

同态加密（Homomorphic Encryption，简称HE）是很久以前密码学界就提出来的一个Open
Problem。早在1978年，Ron Rivest, Leonard Adleman, 以及Michael L.
Dertouzos就以银行为应用背景提出了这个概念[RAD78]。其中Ron Rivest和Leonard
Adleman分别就是著名的RSA算法（一种非对称加密算法）中的R和A。至于中间的S，Adi
Shamir，现在仍然在为密码学贡献新的工作。

什么是同态加密？
提出第一个构造出全同态加密（Fully Homomorphic Encryption）[Gen09]的Craig Gentry给出的直观定义最好：

A way to delegate processing of your data, without giving away access to it.
一种在不放弃访问权限的情况下委托数据处理的方法。

这是什么意思呢？一般的加密方案关注的都是数据存储安全。即，我要给其他人发送数据，或者要在计算机上存数据，需要对数据进行加密后再发送或者存储。没有密钥的用户，不可能从加密结果中得到有关原始数据的任何信息。只有拥有密钥的用户才能够正确解密，得到原始的内容。我们注意到，这个过程中用户是不能对加密结果做任何操作的，只能进行存储、传输。对加密结果做任何操作，都将会导致错误的解密，甚至解密失败。

但同态加密方案关注的是数据处理安全。同态加密提供了一种对加密数据进行处理的功能。也就是说，其他人可以对加密数据进行加工处理，但是加工处理过程不会泄露任何原始内容。同时，拥有密钥的用户对加工处理过的数据进行解密后，得到的正好是明文数据处理后的结果。


‍♂️个理解

有个A用户买到了一大块金子，她想让工人把这块金子打造成一个项链。但是工人在打造的过程中有可能会偷金子啊，因此能不能有一种方法，既让工人可以对金块进行加工（delegate
processing of your data），又无法得到任何金子（without giving away access to it）

A可以这么做：
● 将金子锁在一个密闭的盒子里面，这个盒子安装了一个手套。
● 工人可以带着这个手套，对盒子内部的金子进行处理。但盒子是锁着的，工人不仅拿不到金块，连处理过程中掉下的任何金子都拿不到。
● 加工完成后。A拿回这个盒子，把锁打开，就得到了金子。

这个盒子的样子大概是这样的：

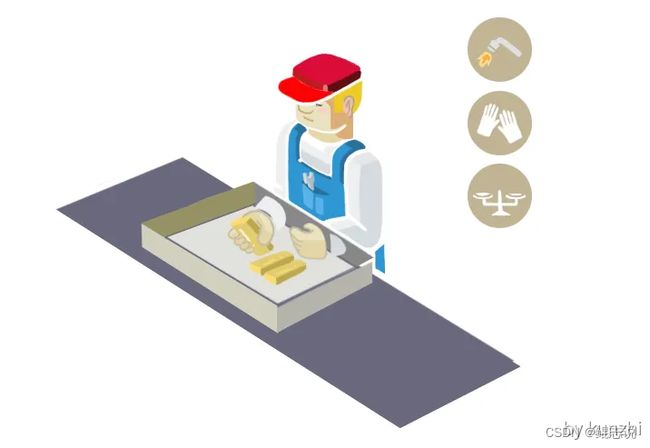
这里面的对应关系是：
● 盒子：加密算法
● 盒子上的锁：用户密钥
● 将金块放在盒子里面并且用锁锁上：将数据用同态加密方案进行加密
● 加工：应用同态特性，在无法取得数据的条件下直接对加密结果进行处理
● 开锁：对结果进行解密，直接得到处理后的结果

---

同态加密具体如何定义？

我们以云计算应用场景为例：

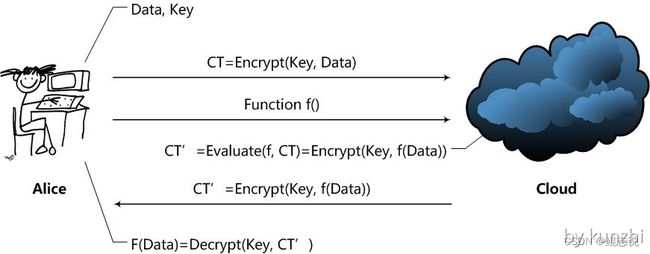
Alice通过Cloud，以同态加密（以下简称HE）处理数据的整个处理过程大致是这样的：

1. Alice对数据进行加密。并把加密后的数据发送给Cloud；
2. Alice向Cloud提交数据的处理方法，这里用函数f来表示；
3. Cloud在函数f下对加密数据进行处理，并且将处理后的结果发送给Alice；
4. Alice对数据进行解密，得到结果。
   
   

据此，我们可以很直观的得到一个HE方案应该拥有的函数：

KeyGen函数：密钥生成函数。这个函数应该由Alice运行，用于产生加密数据Data所用的密钥Key。当然了，应该还有一些公开常数PP（Public Parameter）；
Encrypt函数：加密函数。这个函数也应该由Alice运行，用Key对用户数据Data进行加密，得到密文CT（Ciphertext）；
Evaluate函数：评估函数。这个函数由Cloud运行，在用户给定的数据处理方法f下，对密文进行操作，使得结果相当于用户用密钥Key对f(Data)进行加密。
Decrypt函数：解密函数。这个函数由Alice运行，用于得到Cloud处理的结果f(Data)。


那么， f函数应该是什么样子的呢？根据函数f的限制条件不同，HE方案实际上分为了两类：
● 全同态加密(Fully Homomorphic Encryption，简称 FHE)：这意味着HE方案支持任意给定的f函数，只要这个f函数可以通过算法描述，用计算机实现。显然，FHE方案是一个非常棒的方案，但是计算开销极大，暂时还无法在实际中使用。
● 类同态加密(Somewhat Homomorphic Encryption，简称 SWHE) 或部分同态加密(partial homomorphic encryption, 简称PHE)：这意味着HE方案只支持一些特定的f函数。SWHE方案稍弱，但也意味着开销会变得较小，容易实现，现在已经可以在实际中使用。

---

主流同态加密算法原理

满足有限运算同态性而不满足任意运算同态性的加密算法称为半同态加密。典型的半同态加密特性包括乘法同态、加法同态、有限次数全同态等。

乘法同态加密算法

简单理解：

• 原始数据：$\begin{array}{c}{x}_1，x_2\end{array}$
• 通过对原始数据加密（这里简化举例为三次方）
  • 则$\begin{array}{c}{x}_1\end{array}$加密后数据为：$x_1^3$
  • 则$\begin{array}{c}{x}_2\end{array}$加密后数据为：$x_2^3$
• 对加密数据做乘法处理：则$(x_1^3)\ast (x_2^3)$,即$(x_1\ast x_2{)}^3$
• 对加密数据处理结果用解密（这里简化举例为开根号）

在实际应用中，密文乘法同态性的需求场景不多，因此乘法同态性通常偶然存在于已有的经典加密算法中。满足乘法同态特性的典型加密算法包括1977年提出的RSA公钥加密算法和1985年提出的ElGamal公钥加密算法等。

① RSA算法

RSA算法是最为经典的公钥加密算法，至今已有40余年的历史，其安全性基于大整数分解困难问题。在实际应用中，RSA算法可采用RSA_PKCS1_PADDING、RSA_PKCS1_OAEP_PADDING等填充模式，根据密钥长度（常用1024位或2048位）对明文分组进行填充，而只有不对明文进行填充的原始RSA算法才能满足乘法同态特性。由于原始的RSA不是随机化加密算法，即加密过程中没有使用随机因子，每次用相同密钥加密相同明文的结果是固定的。因此，利用RSA的乘法同态性实现同态加密运算会存在安全弱点，攻击者可能通过选择明文攻击得到原始数据。

一些基本的数学知识

• 质数（素数） p：只有1和他本身能被自己整除。
• 互质：如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系,比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。
• 欧拉函数φ(n)：小于n的正整数中，与n互质的整数的个数。例如φ(8)=4（因为小于8的正整数中只有1,3,5,7与8互质）
  • 若n为质数，则φ(n)=n-1
  • n如果可以分为两个质数（p,q）的乘积，则φ(n)=φ(p*q)=φ§φ(q)=(p-1)(q-1)
• 欧拉定理：如果两个正整数a和n互质，则：a^φ(n)≡1 mod n。特别的，当n为质数时： a^(n-1)≡1 mod n
• 模反元素: 如果两个正整数a和n互质，那么一定可以找到整数b，满足：a×b≡1 mod n（ab-1 被n整除，或者说ab被n除的余数是1）这时，b就叫做a的"模反元素"。

RSA的具体过程

假设alice想要通过rsa算法在公网上，将消息加密传递给bob，他们应该怎么做呢？分为以下几个步骤：
1.bob生成公私钥，将公钥在网上公开，私钥自己保存
2.alice通过bob的公钥加密明文消息m，得到密文c，并将密文c传递给bob
3.bob用自己的私钥解密密文c，得到明文m

秘钥的产生

• bob选择两个保密的大质数p和q（这里假设是p=61,q=53）
  • 计算n=p×q=61×53=3233，φ(n)=φ(p*q)=φ§φ(q)=(p-1)(q-1)=60×52=3120
    • 这里 n的长度就是秘钥的长度 。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。
• 选一个整数e，满足1< e < φ(n)，且e与φ(n) 互质
  • bob就在1到3120之间，随机选择了17。（实际应用中，常常选择65537。）
• 求解e关于φ(n)的模反元素d（由于e与φ(n)互质，所以d一定存在）
  • ed ≡ 1 (mod φ(n)) 等价于 ed - 1 = kφ(n)，这里就是17d-1 =3120k，求得(d,k)=(2753,-15)，即 d=2753。
• n和e封装成公钥，n和d封装成私钥
  • 这个例子中 n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）

加密

假设alice要向bob发送明文信息m，则用bob的公钥 (n=3233,17,e=17) 对m进行加密。
并且加密时必须将明文进行比特串分组，保证每个分组对应的十进制数小于n，即保证m c ≡ m^e (mod n)
这里m假设是65，那么可以算出下面的等式：65^17 ≡ 2790 (mod 3233)
于是，c等于2790，alice就把2790发给了bob。

解密

bob拿到c(2790)以后，就用自己的私钥(n=3233, d=2753) 进行解密。
m ≡ c^d (mod n)
那么，bob算出 2790^2753 ≡ 65 (mod 3233)
因此，bob知道了alice加密前的原文就是65。

验证了 RSA 算法的乘法同态性

给出两个明文m1和m2，使用上述方法加密后得到两个密文，
c1= E(m1) =m1^ ( )，
c2= E(m2) = m2^ ( )，
将两个密文相乘得到：c1∗ c2= E(m1) ∗E(m2) = m1^∗ m2^ ( )，
由于E(m1m2) = (m1m2)( )，所以可以得出E(m1m2) = E(m1) ∗ E(m2)，

验证了 RSA 算法的乘法同态性。

java代码简单实现

import java.math.BigInteger;
import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.interfaces.RSAPrivateKey;
import java.security.interfaces.RSAPublicKey;
import java.util.Random;

public class RSATest {
    public static void main(String[] args) throws Exception{
        // 1. 生成RSA密钥对
        // 获取指定算法的密钥对生成器
        KeyPairGenerator gen = KeyPairGenerator.getInstance("RSA");
        // 初始化密钥对生成器（指定密钥长度, 使用默认的安全随机数源）
        gen.initialize(512);
        // 随机生成一对密钥（包含公钥和私钥）
        KeyPair keyPair = gen.generateKeyPair();
        // 获取 公钥 和 私钥
        RSAPublicKey pubKey = (RSAPublicKey)keyPair.getPublic();
        RSAPrivateKey priKey = (RSAPrivateKey)keyPair.getPrivate();
        // 获得公私钥 和 公共模数
        BigInteger E = pubKey.getPublicExponent();
        BigInteger D = priKey.getPrivateExponent();
        BigInteger N = pubKey.getModulus();
        System.out.println("E:" + E);
        System.out.println("D:" + D);
        System.out.println("N:" + N);

        BigInteger m1 = BigInteger.valueOf(new Random().nextInt(Integer.MAX_VALUE));
        BigInteger m2 = BigInteger.valueOf(new Random().nextInt(Integer.MAX_VALUE));

        // 加密
        BigInteger C1 = m1.modPow(E, N);
        BigInteger C2 = m2.modPow(E, N);
        // 密文相乘
        BigInteger C = C1.multiply(C2).mod(N);
        // 解密
        BigInteger Mc = C.modPow(D, N);
        // 验证
        BigInteger val = m1.multiply(m2);
        System.out.println("原始数据数据m1:" + m1 + "，m2:" + m2);
        System.out.println("m1加密后数据C1:" + C1);
        System.out.println("m2加密后数据C2:" + C2);
        System.out.println("C:" + C);
        System.out.println("Mc:" + Mc);
    }
}

python代码简单实现

import rsa
import rsa.core

# pip install rsa
(public_key, private_key) = rsa.newkeys(256)
print('1.密钥生成')
print('生成公钥')
print('public key:', public_key)
print(public_key.n,public_key.e)
print()
print('生成私钥')
print('private key:', private_key)
print(private_key.n,private_key.d)
print()
print('2.加密')
enc1 = rsa.core.encrypt_int(2, public_key.e, public_key.n)
print('加密3 结果 enc1:  ' + str(enc1))
enc2 = rsa.core.encrypt_int(20, public_key.e, public_key.n)
print('加密15 结果 enc2:  ' + str(enc2))
print()
result = enc1 * enc2
print('3.同态运算')
print('相乘 result=' + str(enc1) + ' * ' + str(enc2) + '=' + str(result))
print()
decrypt_result = rsa.core.decrypt_int(result, private_key.d, public_key.n)
print('4.解密:' + str(decrypt_result))
print()

② ElGamal算法

ElGamal算法是一种基于Diffie-Hellman离散对数困难问题的公钥密码算法，可实现公钥加密和数字签名功能，同时满足乘法同态特性。ElGamal是一种随机化加密算法，即使每次用相同密钥加密相同明文得到的密文结果也不相同，因此不存在与RSA算法类似的选择明文攻击问题，是ISO同态加密国际标准中唯一指定的乘法同态加密算法。

加法同态加密算法

Paillier算法是1999年提出的一种基于合数剩余类问题的公钥加密算法，也是目前最为常用且最具实用性的加法同态加密算法，已在众多具有同态加密需求的应用场景中实现了落地应用，同时也是ISO同态加密国际标准中唯一指定的加法同态加密算法。此外，由于支持加法同态，所以Paillier算法还可支持数乘同态，即支持密文与明文相乘。

python代码简单实现

import random

import phe
from phe import EncodedNumber, paillier
from phe.util import invert, powmod, getprimeover, isqrt
import numpy as np

# test
if __name__ == "__main__":
    public_key, private_key = paillier.generate_paillier_keypair(n_length=10)
    print('pub', public_key.g, public_key.n)
    print('priv', private_key.p, private_key.q)
    A=[3,32]
    print('A', A)
    enA=[public_key.encrypt(x) for x in A]
    print(enA[0].ciphertext(False))
    print(enA[0].ciphertext(False).bit_length())
    B=[4,16]
    print('B', B)
    enB=[public_key.encrypt(x) for x in B]
    print(enB[0].ciphertext(False))
    print(enB[0].ciphertext(False).bit_length())
    en=np.add(enA,enB)
    print(en[0].ciphertext(False))
    print(en[0].ciphertext(False).bit_length())
    for x in en:
        print(private_key.decrypt(x))

  

有限全同态加密算法

2005年提出的Boneh-Goh-Nissim方案是一种基于双线性映射的公钥密码方案，支持任意次加法同态和一次乘法同态运算。方案中的加法同态基于类似Paillier算法的思想，而一次乘法同态基于双线性映射的运算性质。由于双线性映射运算会使得密文所在的群发生变化，因此仅能支持一次乘法同态运算，但仍支持对乘法后的密文进一步作加法同态运算。

---

同态加密的优势

我们当前的技术体系，建立在密码学基础上，工程中会用到很多密码学组件，非对称加密、可交互加密等，在这层之上，构建了很多安全算子，例如同态加密、不经意传输、秘密分享等。

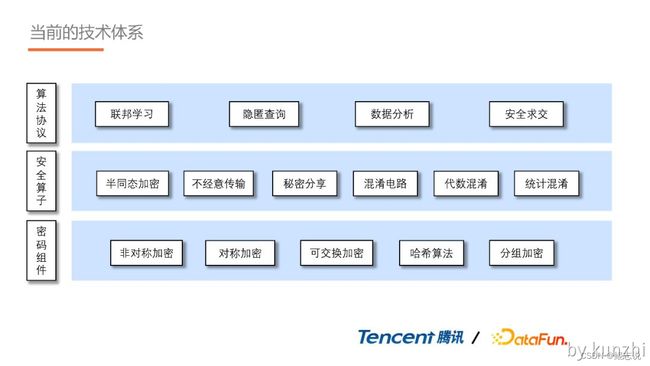
非全同态加密存在的问题

1.非通用计算

非通用计算标准，需要根据具体的问题双方来制定不同的计算标准。概括来说就是一事一协议，新的计算需要在合作各方去使用同一个协议。一事一协议这种非通用计算，使用当前密码学技术来构建算子在工程实践中并非理想的解决方案。

2.计算逻辑的暴露

计算逻辑暴露的问题跟一事一协议紧密相关，两个数据拥有方需要遵循同一协议来计算某些结果。例如一个数据拥有方想要跟对方比较一个统计值的大小，它需要告诉对方要用到一个比较大小的协议。对方确认自己拥有同样的协议之后，才可能执行比较操作。
这样的话，任何参与方的计算过程中，计算逻辑都会暴露给其他参与方，参与者无法对计算逻辑本身进行保护。虽然计算逻辑听起来并不重要，但实际上在真实的金融场景中，一些模型及方法的计算逻辑可能是公司的核心机密，所以计算逻辑暴露对隐私计算来说是一个很重要的问题。

3.多轮次交互

在进行多协议交互时，其网络通信和交换的频次也会更加频繁，就会对网络带宽、网速和网络的稳定性产生较高要求。
在一些金融场景中，参与方与金融机构之间往往通过专线连接信息系统，当数据传输量较大，交换频次非常多时，往往出现整个计算流程被拖得较慢。另外当网络交换频次非常多时，对网络稳定性要求就比较高，断连、延迟等网络波动可能会使计算过程出现失败。

4.可信执行环境

面对上述多轮次交互带来的网络带宽、网速和网络稳定性问题，我们能否采用涉及硬件级安全计算的解决方案，例如使用可信执行环境。在实际业务的方案推进这种可信执行环境落地过程中，施工方可能会遇到一些非技术类问题，实际业务的客户比较关心特殊硬件的成本与安全：

• 需要特殊硬件支持，部署成本高
• 可信性依赖于国外硬件厂商

金融机构通常自建处理大数据业务的计算集群，已经投入大量成本，如果要重建一个基于可信执行环境的集群，成本是巨大的。另外，目前可信环境的硬件厂商主要来自国外，例如英特尔、AMD等，仅仅基于厂商的描述，客户无法完全认可这套设备可信性，信任度较低。
所以当我们遇到这类场景，需要解决业务机密问题，同时不能采用可信计算环境的时候，全同态加密就体现出它的优势。

---

标准化进展

1.半同态加密标准化

2019年5月，国际标准化组织ISO发布了同态加密标准（ISO/IEC 18033-6:2019）。该标准仅涉及半同态加密，具体包含两种较为成熟的半同态加密机制：ElGamal乘法同态加密和Paillier加法同态加密，并规定了参与实体的参数和密钥生成、数据加密、密文数据解密、密文数据同态运算等步骤的具体过程。

2.全同态加密标准化

2017年7月，来自学术界、工业界和政界的相关领域研究人员组成了全同态加密标准化开放联盟HomomorphicEncryption.org，在微软研究院举办了首届全同态加密标准化研讨会，开始共同推进全同态加密标准草案的编写工作，并发布了全同态加密安全标准、API标准、应用标准三份白皮书。迄今为止，HomomorphicEncryption.org在三年内已举办五届全同态加密标准化会议，参与成员包括微软、三星SDS、英特尔、IBM、谷歌、万事达卡等企业，以及NIST、ITU等机构的代表和各大高校的学者。在标准化进展方面，HomomorphicEncryption.org已分别于2018年3月和11月发布和更新了全同态加密标准草案。

---

同态加密应用场景

目前，同态加密算法已在区块链、联邦学习等存在数据隐私计算需求的场景实现了落地应用。由于全同态加密仍处于方案探索阶段，现有算法存在运行效率低、密钥过大和密文爆炸等性能问题，在性能方面距离可行工程应用还存在一定的距离。因此，实际应用中的同态加密算法多选取半同态加密（如加法同态），用于在特定应用场景中实现有限的同态计算功能。

1. 外包计算

当用户有数据但没算力资源，可利用同态加密技术对其数据进行加密，依靠第三方云厂商的算力资源进行结果计算。这样在不泄露自己数据隐私的前提下得到了自己想要的结果数据。

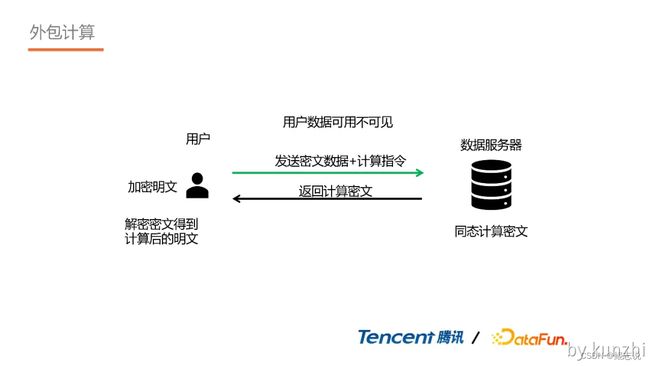
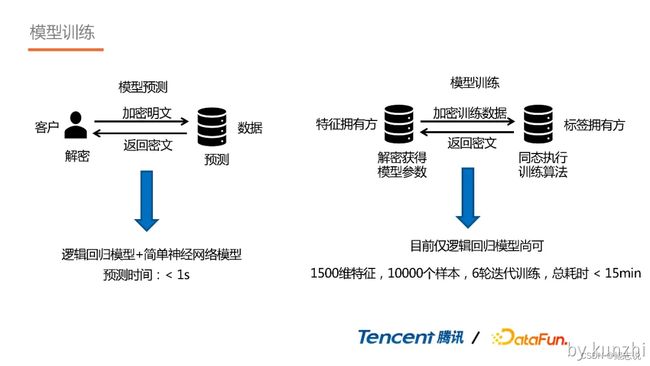
2. 模型训练

在模型训练过程中，标签拥有方对自有标签加密后，传输给特征拥有方。由于全同态加密算法允许对密文进行无限次的加法和乘法运算，因此特征拥有方可在密文空间去执行整个训练算法，并将训练好之后的模型返回给特征任务方进行解密。
在该过程中只需要两轮网络通信，免除了一些频繁的网络交互。同时标签拥有方其模型训练完全自主可控，可以对模型进行灵活调整，而不需要与特征拥有方同时具有相同的协议，因此其计算逻辑也不会暴露。

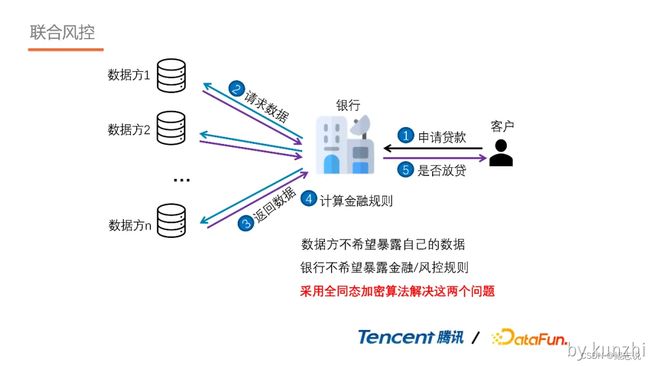
3. 联合风控

在联合风控场景，数据提供方不希望自己的数据泄露给银行，同时银行也不希望自己的风控规则泄露给数据提供方。在这种情况下，可利用全同态加密对数据提供方的数据和银行风控规则进行加密处理，最后根据计算结构来判定是否放贷。

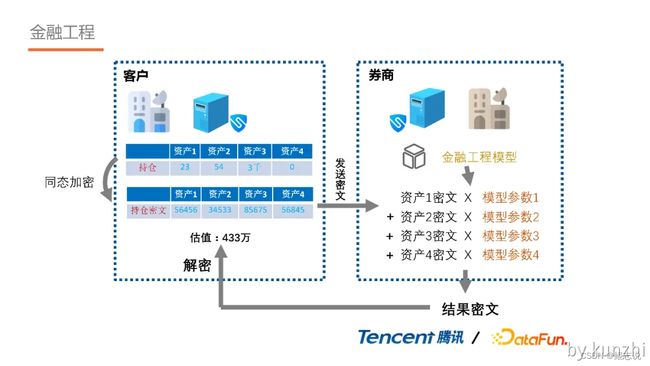
4. 金融工程

在金融工程场景，客户不愿意把自己的持仓泄露给券商，而券商也不愿意将他投入巨大资源的金融工程模型泄露给对方。在这种情况下，可利用全同态加密对客户持仓数据进行加密，作为券商金融工程模型的输入，最后将计算得到的模型结果进行解密来进行资本操作。

---

参考

• 同态加密的实现原理是什么？在实际中有何应用？
• 同态加密的实现原理是什么？在实际中有何应用？
• A Homomorphic Encryption Illustrated Primer
• 同态加密：实现数据的“可算不可见”
• 同态加密技术及其在云计算隐私保护中的应用
• 联邦学习之旅】03 同态加密与 Paillier/RSA
• RSA算法原理（二）
• 深入理解RSA算法