Kaggle竞赛——桑坦德银行客户满意度预测(四)
模型训练与评估
读取数据
#加载数据集
dataset = 'Normal'
train = pd.read_pickle('./data/santander-customer-satisfaction/output/train_normal.pkl')
test = pd.read_pickle('./data/santander-customer-satisfaction/output/test_normal.pkl')
X_train = train.drop(['ID','TARGET'],axis=1)
y_train = train['TARGET'].values
X_test = test.drop('ID',axis=1)
test_id = test['ID']
del train,test
#划分数据集
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, stratify=y_train, test_size=0.15)
X_train.shape, X_val.shape, X_test.shape
我们分别输出训练集、验证集、测试集的shape:
((64617, 336), (11403, 336), (75818, 336))
定义AUC函数和调参函数
ROC:接收器工作曲线
AUC(Area Under the Curve):ROC曲线下面积
接下来我们定义ROC曲线绘制函数
global i
i = 0
def plot_auc(y_true,y_pred,label,dataset = dataset):
'''
给出y_true和y_pred时绘制ROC曲线
dataset:告诉我们使用了哪个数据集
label:告诉我们使用了哪个模型,若label是一个列表,则绘制所有标签的所有ROC曲线
'''
if (type(label) != list) & (type(label) != np.array):
print("\t\t %s on %s dataset \t\t \n" % (label, dataset))
auc = roc_auc_score(y_true, y_pred)
logloss = log_loss(y_true, y_pred) #-(ylog(p) + (1-y)log(1-p)))
label_1 = label + ' AUC=%.3f' % (auc)
# 绘制ROC曲线
fpr, tpr, threshold = roc_curve(y_true, y_pred)
sns.lineplot(fpr, tpr, label=label_1)
x = np.arange(0, 1.1, 0.1) # 绘制AUC=0.5的直线
sns.lineplot(x, x, label="AUC=0.5")
plt.title("ROC on %s dataset" % (dataset))
plt.xlabel('False Positive Rate')
plt.ylabel("True Positive Rate")
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.) # 设置图例在图形外
plt.show()
print("在 %s 数据集上 %s 模型的 logloss = %.3f AUC = %.3f" % (dataset, label, logloss, auc))
# 创建结果数据框
result_dict = {
"Model": label,
'Dataset': dataset,
'log_loss': logloss,
'AUC': auc
}
return pd.DataFrame(result_dict, index=[i])
else:
# 绘制ROC曲线
plt.figure(figsize=(12, 8))
for k, y in enumerate(y_pred):
fpr, tpr, threshold = roc_curve(y_true, y)
auc = roc_auc_score(y_true, y)
label_ = label[k] + ' AUC=%.3f' % (auc)
sns.lineplot(fpr, tpr, label=label_)
x = np.arange(0, 1.1, 0.1)
sns.lineplot(x, x, label="AUC=0.5")
plt.title("Combined ROC")
plt.xlabel('False Positive Rate')
plt.ylabel("True Positive Rate")
plt.legend(bbox_to_anchor=(1.05, 1), loc=2,borderaxespad=0.)
plt.show()
继续定义调参函数
def find_best_params(model, params, cv=10, n_jobs=-1, X_train=X_train):
"""
使用随机搜索RandomizedSearchCV调参,返回最佳模型
"""
random_cv = RandomizedSearchCV(model,
param_distributions=params,
scoring='roc_auc',
n_jobs=n_jobs,
cv=cv,
verbose=2)
random_cv.fit(X_train, y_train)
print("最佳的AUC得分为:%.3f" % (random_cv.best_score_))
print("最佳的参数为:%s" % (random_cv.best_params_))
return random_cv.best_estimator_
随后,我们将使用不同分类模型进行分类,并评估效果。
逻辑回归
逻辑回归我们主要调整的参数有:
- 正则化方式:L1和L2
- 惩罚系数C
- 是否拟合截距
# 初始化模型并设置参数
model_lr = LogisticRegression(class_weight='balanced')
params = {
'penalty': ['l2', 'l1'],
'C': [10.**i for i in np.arange(-3, 3, 1)],
'fit_intercept': [True, False],
}
# 超参数寻优
find_best_params(model_lr, params)
得到的最佳超参数为:
Fitting 10 folds for each of 10 candidates, totalling 100 fits
最佳的AUC得分为:0.798
最佳的参数为:{'penalty': 'l2', 'fit_intercept': True, 'C': 0.001}
# 拟合调参后的模型
model_lr = LogisticRegression(C=0.001, class_weight='balanced')
model_lr.fit(X_train, y_train)
#存储结果并绘制ROC曲线
labels = []
y_preds = []
y_pred = model_lr.predict_proba(X_val)[:,1]
label = "Logistic Regression"
labels.append(label)
y_preds.append(y_pred)
i = 0
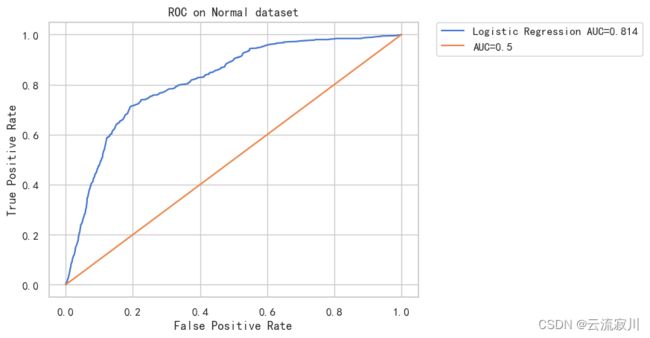
result = plot_auc(y_val, y_pred, label, dataset)
result_df = result
del result
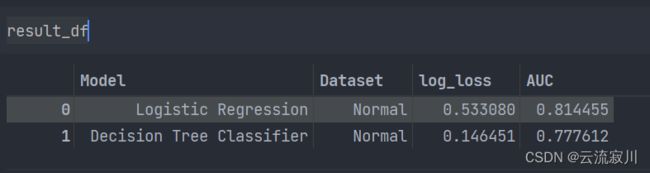
在 Normal 数据集上 Logistic Regression 模型的 logloss = 0.533 AUC = 0.814
决策树(Decision Trees)
下面需要介绍决策树调参常用的四个参数及其意义
max_depth:限制树的最大深度,大于这个深度的,全部剪掉
min_samples_leaf:在节点分支时,表示分支后的节点至少要含有至少min_samples_leaf 个样本,否则这个节点就不分
min_samples_split:在节点分支时,表示这个节点本身必须含有至少min_samples_split个样本,否则这个节点就不分,注意和上面一个参数区分,上面是讲这个节点分支后的节点的含有样本最小个数,而这个参数是将这个节点还没分之前自己本身所含有的样本最小个数
max_features:在节点分裂时,考虑的最大的特征数量,也就是在每一个节点分支划分时,并不是所有的都特征都考虑,而是考虑一部分,大于max_features 的特征都将被舍弃
model_dt = DecisionTreeClassifier(class_weight='balanced')
params = {
'max_depth':[10,100,500,1000,-1],
'min_samples_split':[2,5,10,100,-1],
'min_samples_leaf':[1,3,5,7,10],
'max_leaf_nodes':[100,500,1000,5000,-1]
}
find_best_params(model_dt,params)
Fitting 10 folds for each of 10 candidates, totalling 100 fits
最佳的AUC得分为:0.707
最佳的参数为:{'min_samples_split': 100, 'min_samples_leaf': 7, 'max_leaf_nodes': 5000, 'max_depth': 1000}
model_dt = DecisionTreeClassifier(class_weight='balanced',max_depth=10,
max_leaf_nodes=500,
min_samples_leaf=10,
min_samples_split=5)
model_dt.fit(X_train,y_train)
cc_model_dt = CalibratedClassifierCV(model_dt,cv='prefit')
cc_model_dt.fit(X_train,y_train)
CalibratedClassifierCV概率校准原理?
执行分类时, 我们经常希望不仅可以预测类标签, 还要获得相应标签的概率. 这个概率给你一些预测的信心. 一些模型可以给你贫乏的概率估计, 有些甚至不支持概率预测. 校准模块可以让您更好地校准给定模型的概率, 或添加对概率预测的支持.
对于不用于模型拟合的新数据, 应进行概率校准. 类 CalibratedClassifierCV 使用交叉验证生成器, 并对每个拆分模型参数对训练样本和测试样本的校准进行估计. 然后对折叠预测的概率进行平均. 已经安装的分类器可以通过:class:CalibratedClassifierCV 传递参数 cv =”prefit” 这种方式进行校准. 在这种情况下, 必须手动注意模型拟合和校准的数据是不相交的.
1、什么是概率校准?为什么需要概率校准?
众所周知,对于一个分类模型而言,其主要的任务预测未知样本属于哪个预定义的类别。但在某些场景中,我们不仅希望得到样本的类别标签,也希望知道这样分类的把握有多大。例如,银行在对客户进行评分时,并不满足于识别出该用户是否存在信用风险,更希望能够确定客户存在信用风险的概率,以便计算客户违约带来的期望损失,使得银行能够准备充足的资本以应对风险。
我们知道,有一些模型本身的输出可以代表概率,如逻辑回归和朴素贝叶斯模型;但一些复杂的非线性机器学习算法是无法直接进行概率预测的。因此,有必要对分类结果进行再学习以得到概率,这就是通常意义上说的概率校准。
事实上,概率校准不仅能够将非概率分类模型的输出转化为概率,而且也能够对概率分类模型的结果进行进一步修正。例如,在经过概率校准的逻辑回归模型输出的所有概率为0.8的样本中,大约有80%的样本实际上确实属于正例——在校准之前,可能结果并不是这样。
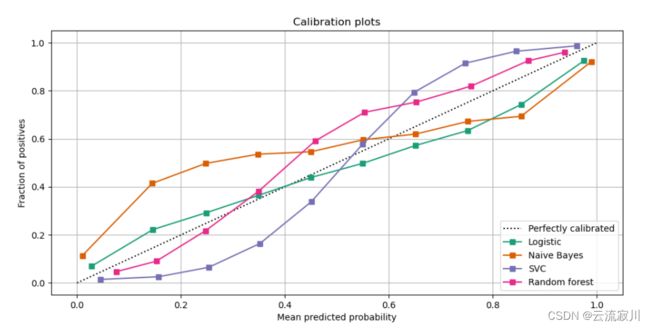
下面给出一篇博客,他将概率校准原理讲解的通俗易懂:
概率校准原理及其实现
我们回到决策树的模型训练过程,在model_dt拟合数据并进行概率校准之后,我们在测试集上进行分类并输出ROC曲线:
y_pred = cc_model_dt.predict_proba(X_val)[:, 1]
label = "Decision Tree Classifier"
labels.append(label)
y_preds.append(y_pred)
i += 1
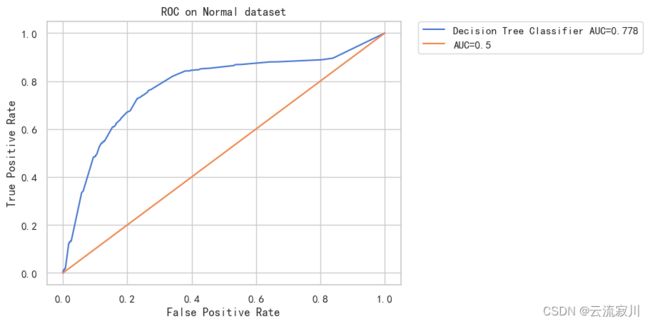
result = plot_auc(y_val, y_pred, label)
result_df = result_df.append(result)
del result
在 Normal 数据集上 Decision Tree Classifier 模型的 logloss = 0.146 AUC = 0.778
随机森林(Random Forest)
同样的我们使用交叉验证的方法进行一个寻参调优的过程:
model_rf = RandomForestClassifier(class_weight='balanced')
params = {
'n_estimators': [1000, 2000],
'max_depth': [1000, 2000],
'min_samples_split': [100, 500],
'min_samples_leaf': [3, 5],
'max_leaf_nodes': [100, 250]
}
find_best_params(model_rf, params, cv=3)
得到的最佳参数为:
Fitting 3 folds for each of 10 candidates, totalling 30 fits
最佳的AUC得分为:0.817
最佳的参数为:{'n_estimators': 1000, 'min_samples_split': 500, 'min_samples_leaf': 3, 'max_leaf_nodes': 250, 'max_depth': 1000}
我们继续基于最佳参数进行模型拟合:
model_rf = RandomForestClassifier(bootstrap=True, ccp_alpha=0.0, class_weight='balanced',
criterion='gini', max_depth=2000, max_features='auto',
max_leaf_nodes=250, max_samples=None,
min_samples_leaf=3, min_samples_split=500,
min_weight_fraction_leaf=0.0, n_estimators=2000,
n_jobs=10, oob_score=False, random_state=42,
verbose=0, warm_start=False)
model_rf.fit(X_train, y_train)
cc_model_rf = CalibratedClassifierCV(model_rf, cv='prefit')
cc_model_rf.fit(X_train, y_train)
画出ROC曲线:
y_pred = cc_model_rf.predict_proba(X_val)[:, 1]
label = "Random Forest Classifier"
labels.append(label)
y_preds.append(y_pred)
i += 1
result = plot_auc(y_val, y_pred, label)
result_df = result_df.append(result)
del result
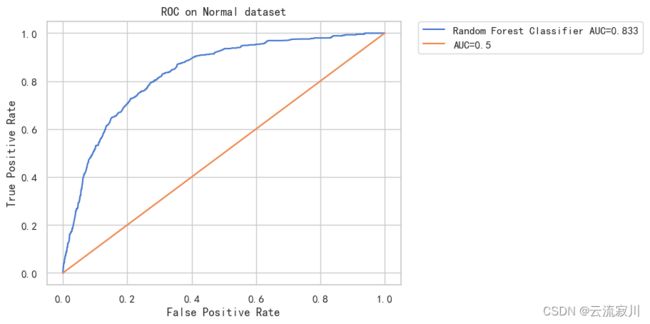
在 Normal 数据集上 Random Forest Classifier 模型的 logloss = 0.137 AUC = 0.833
采用bagging集成的随机森林AUC值达到了0.833,是目前最高的,说明集成法确实能给当前的分类问题的效果带来提升,下面我们还可以考虑两种boosting集成算法的分类效果
XGBoost模型(XGBClassifier)
由于XGB的调参过程较为复杂,这里我们直接采用调好的最优参数进行训练
model_xgb = xgb.XGBClassifier(n_jobs=-1,
nthread=-1,
scale_pos_weight=1.,
learning_rate=0.01,
colsample_bytree=0.5,
subsample=0.9,
objective='binary:logistic',
n_estimators=1000,
reg_alpha=0.3,
max_depth=5,
gamma=5,
random_state=42)
#%%
%%time
eval_metric = ['error', 'auc']
eval_set = [(X_train, y_train), (X_val, y_val)]
model_xgb.fit(X_train, y_train, eval_set=eval_set,
eval_metric=eval_metric, early_stopping_rounds=50, verbose=20)
early_stopping_rounds表示早停次数为50,即在50次内验证集AUC不再提升我们就停止迭代
verbose表示每20次显示一次结果
特别的,在训练过程中,我们分别打印出每20次迭代的训练结果,这里我们仅打印前两百次
[0] validation_0-error:0.03957 validation_0-auc:0.75894 validation_1-error:0.03955 validation_1-auc:0.77028
[20] validation_0-error:0.03957 validation_0-auc:0.81460 validation_1-error:0.03955 validation_1-auc:0.81464
[40] validation_0-error:0.03957 validation_0-auc:0.82008 validation_1-error:0.03955 validation_1-auc:0.81856
[60] validation_0-error:0.03957 validation_0-auc:0.82172 validation_1-error:0.03955 validation_1-auc:0.82104
[80] validation_0-error:0.03957 validation_0-auc:0.82368 validation_1-error:0.03955 validation_1-auc:0.82384
[100] validation_0-error:0.03957 validation_0-auc:0.82574 validation_1-error:0.03955 validation_1-auc:0.82560
[120] validation_0-error:0.03957 validation_0-auc:0.82612 validation_1-error:0.03955 validation_1-auc:0.82554
[140] validation_0-error:0.03957 validation_0-auc:0.82678 validation_1-error:0.03955 validation_1-auc:0.82569
[160] validation_0-error:0.03957 validation_0-auc:0.82786 validation_1-error:0.03955 validation_1-auc:0.82654
[180] validation_0-error:0.03957 validation_0-auc:0.82922 validation_1-error:0.03955 validation_1-auc:0.82750
[200] validation_0-error:0.03956 validation_0-auc:0.83156 validation_1-error:0.03955 validation_1-auc:0.82869
训练结束后我们输出一下最优的AUC得分和迭代次数:
model_xgb.best_score, model_xgb.best_iteration
(0.842974, 902)
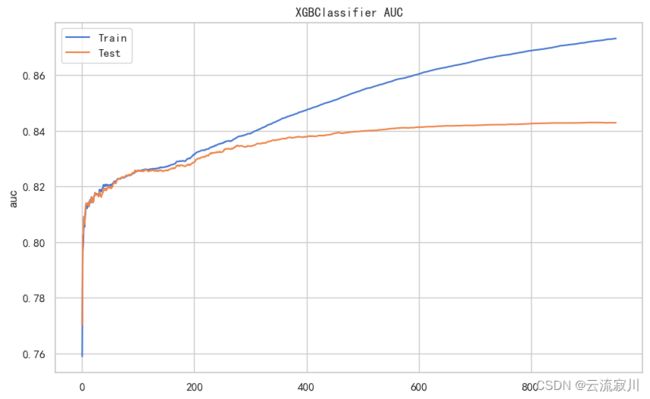
为了便于直观的展现AUC的变化过程,我们直接绘制AUC随迭代次数增加的变化折线图:
# 基于迭代次数的调参曲线
results = model_xgb.evals_result_
auc_train = results['validation_0']['auc']
auc_val = results['validation_1']['auc']
fig, ax = plt.subplots(figsize=(10, 6))
epochs = len(auc_val)
ax.plot(range(0, epochs), auc_train, label='Train')
ax.plot(range(0, epochs), auc_val, label='Test')
ax.legend()
plt.title(model_xgb.__class__.__name__ + ' ' + 'AUC')
plt.ylabel('auc')
plt.show()
print("验证集上最大AUC:%.3f" % (max(auc_val)))
print("最优迭代次数epochs:%i" % (auc_val.index(max(auc_val))))
验证集上最大AUC:0.843
最优迭代次数epochs:902
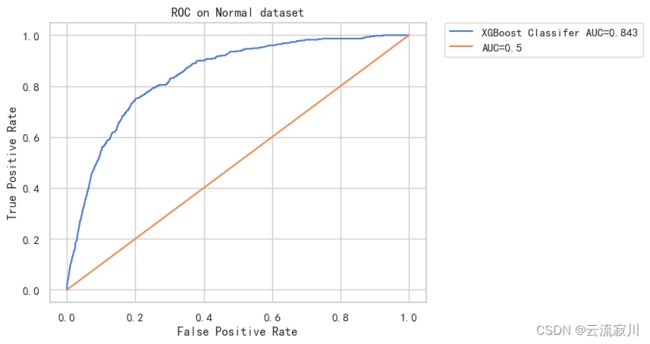
在 Normal 数据集上 XGBoost Classifer 模型的 logloss = 0.134 AUC = 0.843
LGB模型(LightGBM)
LGB模型我们采用与上面同样的策略
model_lgb = lgb.LGBMClassifier(n_jobs=-1,
nthread=-1,
scale_pos_weight=1.,
learning_rate=0.01,
colsample_bytree=0.5,
subsample=0.8,
objective='binary',
n_estimators=1000,
reg_alpha=0.3,
max_depth=7,
random_state=42)
eval_metric = ['binary_logloss', 'auc']
eval_set = [(X_train, y_train), (X_val, y_val)]
model_lgb.fit(X_train, y_train, eval_set=eval_set,
eval_metric=eval_metric, early_stopping_rounds=50, verbose=20)
# 基于迭代次数的调参曲线
results = model_lgb.evals_result_
auc_train = results['training']['auc']
auc_val = results['valid_1']['auc']
fig, ax = plt.subplots(figsize=(10, 6))
epochs = len(auc_val)
ax.plot(range(0, epochs), auc_train, label='Train')
ax.plot(range(0, epochs), auc_val, label='Test')
ax.legend()
plt.title(model_lgb.__class__.__name__ + ' ' + 'AUC')
plt.ylabel('auc')
plt.show()
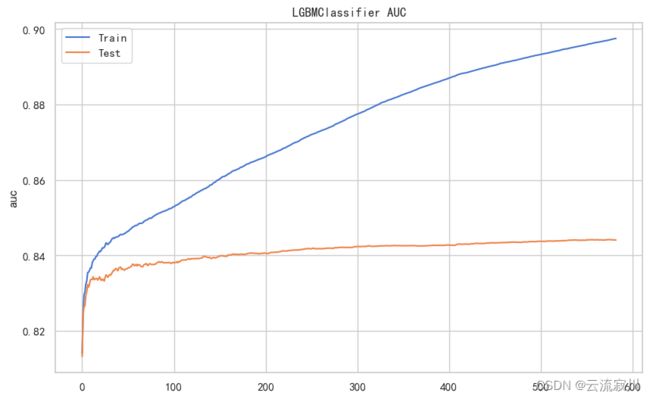
print("验证集上最大AUC:%.3f" % (max(auc_val)))
print("最优迭代次数epochs:%i" % (auc_val.index(max(auc_val)) + 1))
#模型拟合
y_pred = model_lgb.predict_proba(X_val)[:, 1]
label = "LightGBM Classifer"
labels.append(label)
y_preds.append(y_pred)
i += 1
result = plot_auc(y_val, y_pred, label)
result_df = result_df.append(result)
del result
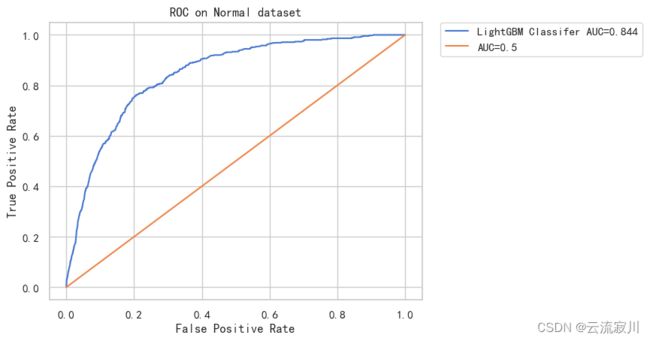
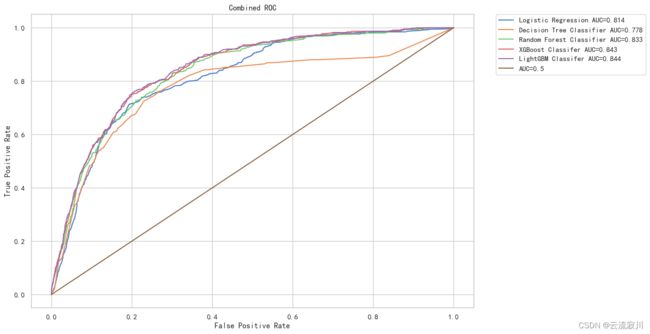
至此,我们已经完成了模型训练和评估的全部工作,我们可以将模型结果进行一个汇总。
模型结果汇总
模型训练结果
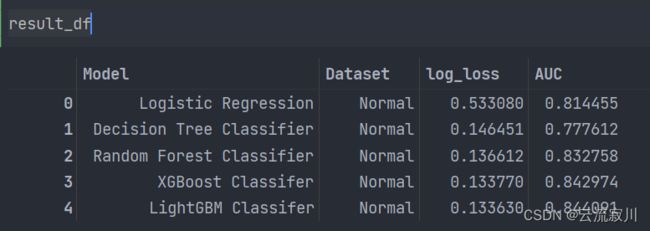
我们可以看出,采用三种集成模型给AUC带来了很大的提升,其中LGB模型在Normal数据集上的表现最佳,AUC达到了0.844