人工智能第四章第四丶五和六节知识总结

4.4归结演绎推理

（1）子句集及其简化

子句和子句集

①原子谓词公式及其否定统称为文字。

     例如，P(x)、Q(x)、﹁ P(x)、﹁ Q(x)等都是文字

②任何文字的析取式称为子句

     例如，P(x)∨Q(x)，P(x，f(x))∨Q(x，g(x))都是子句

③不含任何文字的子句称为空子句

     由于空子句不含有任何文字，也就不能被任何解释所满足，因此空子句是永假的，不可满足的

空子句一般被记为□或NIL

④由子句或空子句所构成的集合称为子句集

（2）鲁滨逊归结原理
命词逻辑的归结
归结推理的核心是求两个子句的归结式，因此需要先
讨论归结式的定义和性质，然后讨论命题逻辑的归结过
程。

下面给出归结式定义与性质
定义4.18若P是原子谓词公式，则称P与一P为互补文字
定义4.19设C1 和C2是子句集中的任意两个子句，如
果C1中的文字L1与C2中的文字L2互补，那么可从C1和C2
中分别消去L1和L2，并将C1和C2中余下的部分按析取关
系构成一个新的子句C,
则称这一过程为归结，称C
为C.和C,的归结式，称C1和C,为C.的亲本子句。

定理4.2归结式C12是其亲本子句C和C2的逻辑结论。正明:（按定义）设C1= Lv C1 '，C2=一L
v C,'关于解释I为真，则只需证明C12= c' vC2'关于解释I也为真。对于解释I，L和—L中必有一个为假。若L为假，则必有C1'为身o个然就公伊1内1汉，之付与前提假设C为真矛盾，因此只能有C1'为真。同理，若一L为假，则必有C,'为真。因此，必有C12= C1' v C,'关于解释I也为真。即C12是C，和C,的逻辑结论。

上述定理是归结原理中的一个重要定理，由它可得到以下两个推论:
推论1:设C和C,是子句集S中的两个子句，C12是C1和C,的归结式，若用C12代替C1和C,后得到新的子句集S1,则由S1的不可满足性可以推出原子句集S的不可满足性。即:
S,的不可满足性→S的不可满足性
推论2:设C1和C,是子句集S中的两个子句，C12是C1
和C2的归结式，看作不可满足性是等价的。

（3）归结演绎推理的归结策略

①广度优先策略

从S0出发，对0S0中的全部子句作所有可能的归结，得到第一层归结式，把这些归结式的集合记为S1

 用S0中的子句与S1中的子句进行所有可能的归结，得到第二层归结式，把这些归结式的集合记为S2

用S0和S1中的子句与S2中的子句进行所有可能的归结，得到第三层归结式，把这些归结式的集合记为S3

如此继续，知道得出空子句或不能再继续归结为止。

4.5基于规则的演绎推理

（1）规则正向演绎推理

把事实表达式化为非蕴含形式的与/或形的主要步骤如下：

1 利用连接词化规律“P→Q —P vQ”，消去蕴含符号。事实上，在事实表达式中很少有含蕴含符号“”出现，因为可把蕴含式表示成规则。
2 利用摩根定律及量词转换率把“一”移到紧靠谓词的位置，直到每个否定符号的辖域最多只含一个谓词为止。
3 对所得到的表达式进行前束化。
4 对全称量词辖域内的变元进行改名和标准化，对存在量词量化的变量用skolem函数代替，使不同量词约束的变元有不同的名字。
5 消去全称量词，而余下的变元都被认为是全程量词量化的变元。
6 对变元进行换名，使主合取元具有不同的变元名。

（2）规则逆向演绎推理

规则逆向演绎推理过程
规则逆向演绎推理过程是从目标公式的与/或树出发，
不断用B规则的石部i与/以N"H耐m加入到与或树中，配成功的B规则用表有最一般合一匹配弧加入到与或树中,
直到产生某个终止在事实节点上的一致解图为止。所谓一致解图是指在推理过程中所用到的置换应该是一致的。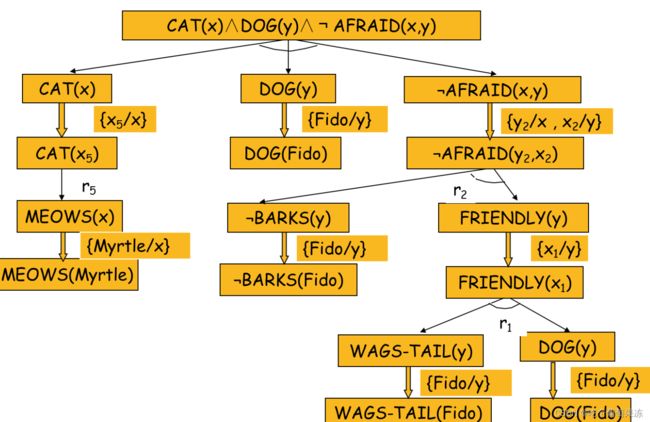

4.6实践：基于规则产生式的推理（本节注重实践，内容略）