java两条直线交点_求两条直线的交点坐标
看UdaCity机器学习大纲,发现入门班中有一条:编写算法计算一组直线或平面的交点。
遂从最简单的直角坐标系两条直线的交点开始,
直线1的方程解析式: 2x-y=0;
直线2的方程解析式: 4x-5y=9;
记录下思考过程
版本一
//求直角坐标系中直线2x-y=0 和 4x-5y=9的交点坐标
$x = 0;
$solution = array();
while(true){
// 2*$x-$y==0; //这样写不能被程序正确理解
$y = 2*$x; //将2x-y=0转化成这样进行赋值操作
//if(2*$x-$y==0 && 4*$x-5*$y==9){ 这样写不能被程序正确理解
if(4*$x-5*$y==9){ //如果此时的x,y坐标也满足第二个解析式则为解
$solution[] = array('x'=>$x,'y'=>$y); //将坐标计入解集合中
break;//由于两条相交的直线最多只有一个交点,只有一个解,找到这个解后直接跳出循环
}
//如果不满足第二个解析式则x变量自减0.1继续下一轮循环
$x -= 0.1;
}
var_dump($solution);
结果
/opt/wwwroot/test/test9.php:19:
array (size=1)
0 =>
array (size=2)
'x' => float -1.5
'y' => float -3
问题
1, 可以看到当x=0不符合要求后,x一直在进行自减,并恰好找到解,这是人为干预的巧合.因为仅凭x=0不是解并不能判断x是正数还是负数,也就不能判断x应该进行自减还是自增操作.如果x进行了x+=0.1的自增操作(实际上一般都是自增),则该循环将一直找不到正解,陷入无限循环.
2, x变量自增减幅度问题.这里得到的解x=-1.5刚好是自变值0.1的整数倍,从而符合条件被找到.如果正解为-1.51,则不会被0.1的自变量命中,它从-1.5和-1.6之间漏过去了,从而也一直找不到这个正解,陷入无限循环.打个比方一批黄金被埋在0-1000米的直路上的某点,某人从0米开始每隔1米挖一个坑,假设黄金被埋在15.1米的地方,而他挖的坑在第15和第16米的地方,则他找不到黄金,即使他每隔0.5米挖一个坑也找不到,除非每隔0.1米挖一个坑,于是他会错过埋在15.01米处的珍珠.这是采样间隔和采样数量的问题.
版本二
为了避免上面的第一个问题,T提出先对x使用一个大小值区间,观察此时的y是如何变化的,再决定对x进行自增还是自减操作
//求直角坐标系中直线2x-y=0 和 4x-5y=9的交点坐标
//起始小值
$xMin = -10000;
//起始大值
$xMax = 10000;
//大小值区间
$xZone = $xMax-$xMin;
//解集合
$solution = array();
function line1($x){
$y = 2*$x;
return $y;
}
function line2($x){
5*$y = 4*$x-9;
return $y;
}
//返回同一个x值时的y差值(y2-y1)
function dY($x){
$y1 = line1($x);
$y2 = line2($x);
return $dY = $y2-$y1;
}
function getFixPoint($xMin, $xMax){
$dYMin = dY($xMin);
$dYMax = dY($xMax);
//判断体系
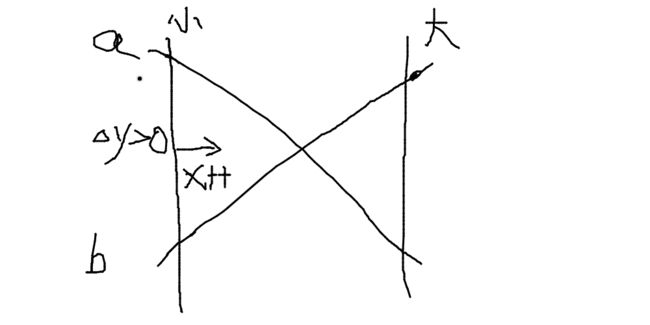
//如果两个x最值的y差值相乘为负,则说明y差值一正一负,两线相交于最值区间内,最小值自增,最大值自减,互相逼近
if($dYMin*$dYMax<0){
$xMin *= 0.5;
$xMax *= 0.5;
getFixPoint($xMin, $xMax); //递归调用本方法
}elseif($dYMin*$dYMax>0){
//如果两个x最值的y差值相乘为正,则说明y差值同号,x的最值区间处于交点的同一侧,需要移动最值区间
if($dYMIn+$dYMax>0){
//如果两个x最值的y差值相加为正,则说明y2>y1,y2在此区间中处于y1上方
//如果y2的斜率大于y1,则交点在区间左边,最值区间往左移,再递归调用本方法
//如果y2的斜率小于y1,则交点在区间右边,最值区间往右移,再递归调用本方法
}elseif($dYMIn+$dYMax<0){
//如果两个x最值的y差值相加为负,则说明y2
//如果y2的斜率大于y1,则交点在区间右边,最值区间往右移,再递归调用本方法
//如果y2的斜率小于y1,则交点在区间左边,最值区间往左移,再递归调用本方法
}
}else{
//如果两个y差值相乘为0,则说明两点相交
}
}
思路
1, 使用区间的方式来判断交点的位置,避免了很多运算,节约了资源.(参考0-1000猜数字的游戏)
2, 斜率之于直线/一次方程/线性,相当于导数之于曲线/二次方程/非线性,在最值区间互相逼近的过程使用了极限的概念,中值定理(?),为接下来的二次/三次/高次方程的求解提供了思路.
缺点:逻辑判断稍微复杂.
版本三
//求直角坐标系中直线2x-y=0 和 4x-5y=9的交点坐标
function getFixPoint($a1,$b1,$c1,$a2,$b2,$c2){
$x=($b2*$c1 - $b1*$c2)/(-1*$a2*$b1 + $a1*$b2);
$y=($a2*$c1 - $a1*$c2)/($a2*$b1 - $a1*$b2);
echo 'x='.$x.'';
echo 'y='.$y.'';
}
getFixPoint(2,-1,0,4,-5,9);
直接使用高斯消元法,so easy!
x=-1.5
y=-3
思考:
1, 使用算法求数学解时,有公式直接套用公式,站在巨人的肩膀上,比自己造轮子要省时省力高效得多;
2, 算法,机器学习,人工智能这些深入进去之后,还是要用微积分,概率论,线性代数,统计学这些基石.