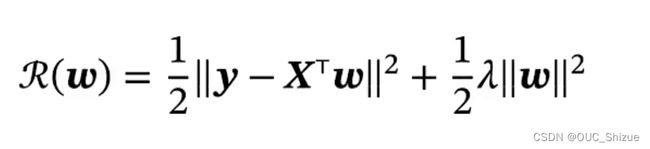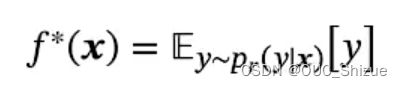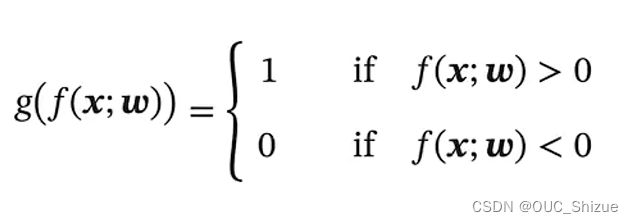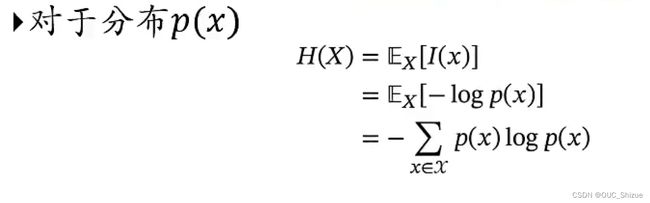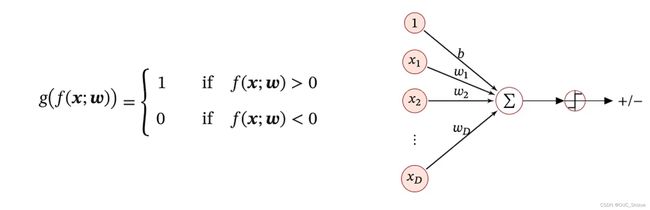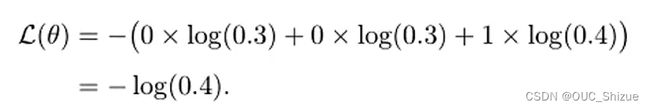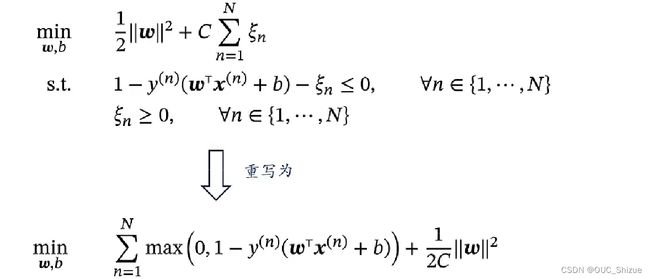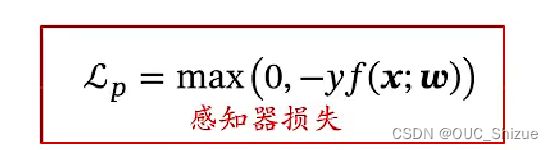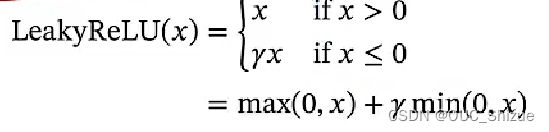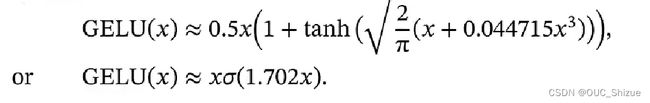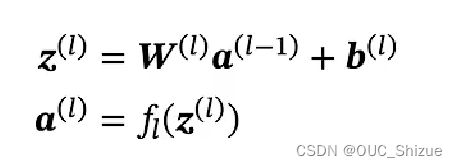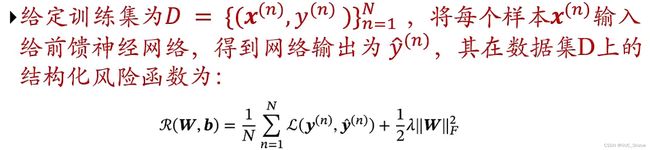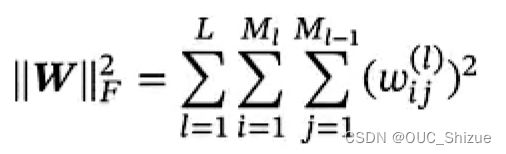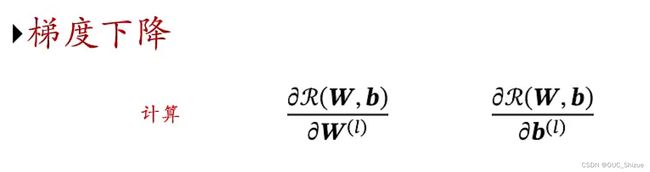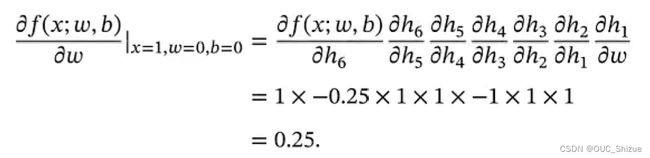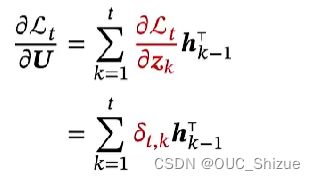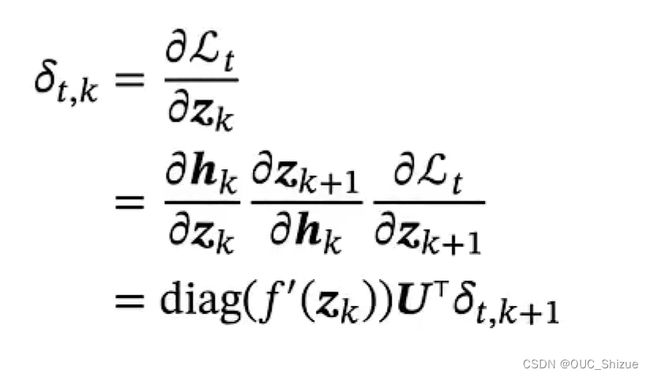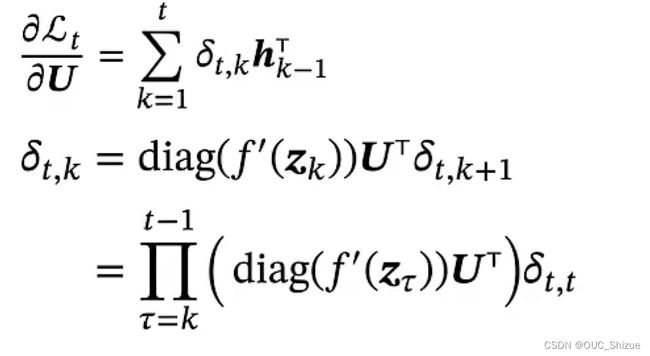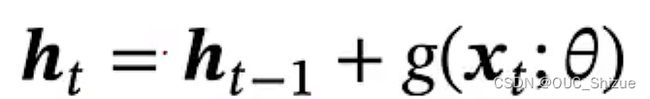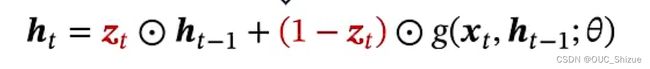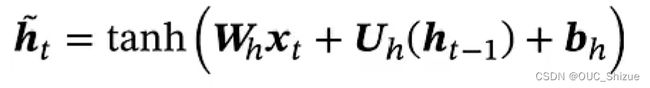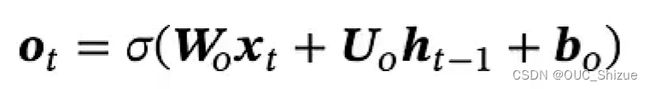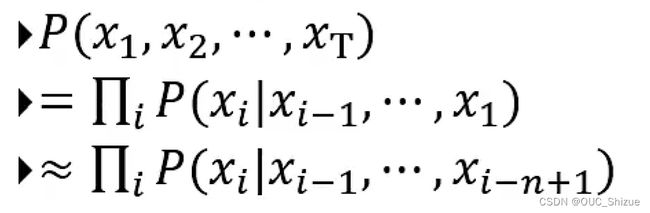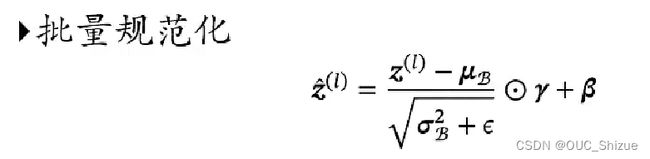OUC_Shizue

Mechine Learning 机器学习笔记

笔记作者:OUC_Shizue 参考课程:复旦大学邱锡鹏《神经网络与深度学习》

第一章：机器学习概论

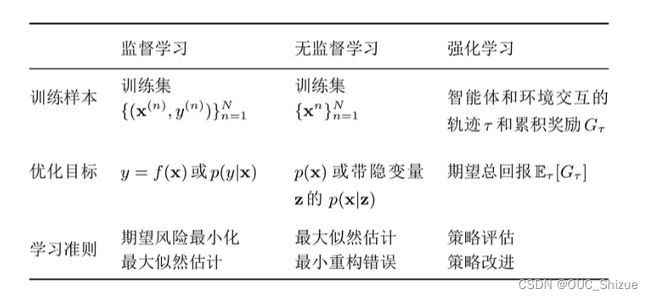
一、机器学习的定义

1、直接定义

机器学习≈计算机自动构建映射函数

Machine Learning 是指从有限的观测数据中学习出具有一般性的规律，并利用这些规律对未知数据进行预测的方法

2、为什么要机器学习

现实世界问题复杂，通过人工总结规律构建映射较为困难；因此我们将其转化为提供数据样本让计算机自动总结规律，构建映射。

3、如何构建输入输出函数

从大量数据中学习规律——function;

即x(representation)->y(label)，如果x，y服从分布P(x,y)，则从分布中取样作为train data，接着构造假设空间F，即一系列f(x)构成的函数族，从中选出最能符合train data映射关系的f’(x)，但此时f’(x)为仅在train data上得到的拟合函数，对该data之外的数据预测效果未知，机器学习的目的就在于让该f’(x)对一切x均有较好预测效果。

4、表示学习介绍

（1）局部表示

one-hot：一维表示，依赖与知识库、规则

例如：

A：[1,0,0,0]
B：[0,1,0,0]
C：[0,0,1,0]
D：[0,0,0,1]

K个元素可以表示K个语义

（2）分布式表示

多维度表示，例如RGB表示所有颜色，k个元素表示2的k次方个语义。
特点：压缩、低维、稠密向量
可将one-hot向量嵌入到空间从而转化为分布式表示。

二、机器学习的类型

1、监督学习

（1）回归问题 Regression

房价预测
股票预测

（2）分类问题 Classification

手写体数字识别
人脸识别
垃圾邮件检测

2、无监督学习

（1）聚类 Clustering

给一些x让计算机自动分类，让类内样本相似，类间样本各不相似

（2）降维 Dimensionality Reduction

将平面数据投影到二维空间，让相似样本距离较近，便于可视化

（3）密度估计 Density Estimation

给定一个空间，将空间内任意一点的密度函数p(x)估计出来

3、强化学习

通过与环境进行交互来学习，例如AlphaGo在下棋过程中以输赢来作为指标

三、机器学习的要素

数据：连续用回归，离散用分类，只给x用无监督；同时需要抽取特征，自动抽取则为表示学习
模型：给定假设空间，从中选择最优模型，对x预测y达到最优效果
学习准则：通过一个准则判断学习效果的好坏
优化算法：给定一个准则后对模型进行优化

四、泛化与正则化

1、泛化误差

经验风险-期望风险=泛化误差
若经验风险过大，期望风险过小，则泛化误差较大，发生过度拟合；因此机器学习的目标为经验风险低，同时泛化误差低

2、优化与正则化的目标

（1）优化

选出一个模型使得经验风险最小，但此时模型往往过拟合，即泛化误差较大

（2）正则化

降低模型复杂度，减小泛化误差

3、正则化 Regularization

（1）定义

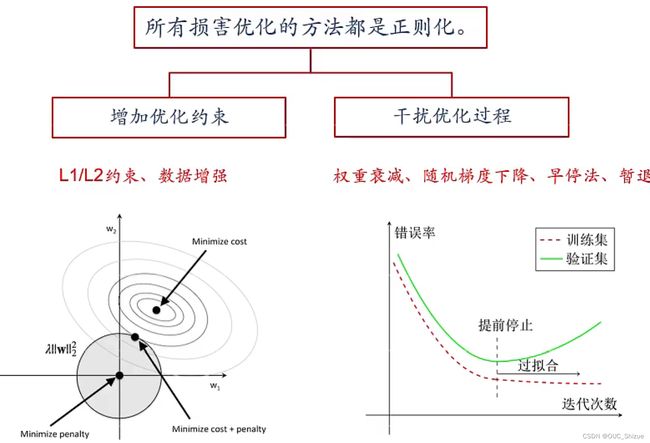
所有损害优化的方法都是正则化

（2）方法

增加优化约束：L1/L2约束、数据增强（构造一些新样本，干扰优化）
干扰优化过程：权重衰减、随机梯度下降、提前停止（使用一个验证集Validation Dataset来测试每次迭代的参数在验证集上是否为最优，如果在验证集上的错误率不再下降则停止迭代）

五、线性回归

1、回归 Regression

2、线性回归 Linear Regression

⊕表示拼接，即在增广矩阵末尾加上该数

3、经验风险最小化 Empirical Risk Minimization，ERM

4、矩阵微积分部分知识

5、结构风险最小化 Structure Risk Minimization，SRM

对应概率中的岭回归 Ridge Regression
当特征之间存在共线性时，X*X转置不可逆，因此通过一个正则化项对w进行约束

6、概率角度看线性回归

（1）似然函数 Likelihood

（2）线性回归中的似然函数

（5）最大似然估计 Maximum Likelihood Estimate，MLE

目标为在给定每一x时，得到标签y的似然最大，即样本中所有似然的连乘最大。
在机器学习中似然常常与指数相关，因此引入log简化计算；例如每个概率为0.01，如果有100个样本则为0.01的100次方，联合概率过小，会产生计算误差
引入log的似然函数也称对数似然函数
最大似然估计的解与最小二乘一致，因此可以理解为最大似然估计与经验风险最小化两种方法等价

（6）贝叶斯视角

贝叶斯学习

贝叶斯公式

即条件概率公式的变形，使得p(x|y)与p(y|x)能够相互转化

后验(posterior)、似然(likelihood)、先验(prior)

p(w|x)∝p(x|w)p(w) 后验∝似然*先验

贝叶斯估计 Bayesian Estimation

代入得

最大后验估计 Maximum A Posteriori Estimation，MAP

求解得到下式，其与结构风险最小化对应

7、四种准则总结

平方误差与概率一一对应，上面理解为对最大值进行限制，下面理解为对w服从以0为中心的高斯分布

平方误差：

经验风险最小化
结构风险最小化

概率：

最大似然估计
最大后验估计

六、多项式回归

1、曲线拟合 Curve Fitting

2、平方误差 Sum-of-Squares

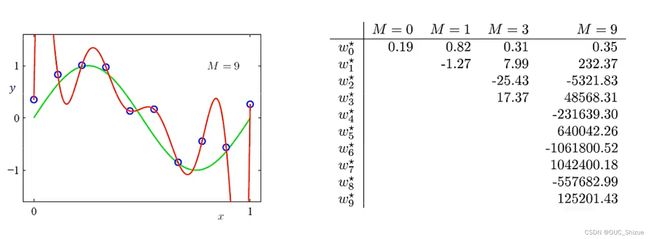
3、如何选择多项式次数 Degree

实质上为模型选择问题(Model Selection Problem)，如果次数太低则欠拟合，太高则过拟合。例如下图中曲线次数选择为9次，穿过了所有训练样本，但在x发生细小波动时结果便产生巨大波动，因为展开次数过大，较小项需要很大系数才能对图像产生影响，因此函数图像边缘出现较大极值。

4、控制过拟合：正则化 Regularization

（1）惩罚大系数

由于存在政策化项，因此此处R(w)为结构风险

引入λ=-18以后例题中曲线拟合效果，可见相较于引入超参数之前，过拟合现象得到了较好控制

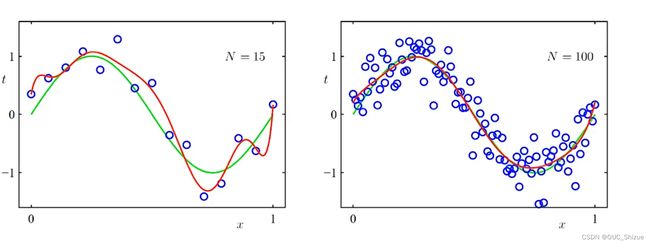
（2）增加train data数量

此处为大数定律的体现，当样本数量无限大的时候经验风险就趋向与期望风险

七、模型选择与“偏差-方差”分解

1、模型选择

拟合能力强的模型一般复杂度会比较高，容易过拟合
如果限制模型复杂度，降低拟合能力，可能会欠拟合

2、如何选择模型

模型越复杂，训练错误越低
不能根据训练错误最低来选择模型
在选择模型时，测试集不可见

3、引入验证集 Validation Set/Development Set

（1）将训练集分为两部分

训练集 Training Set
验证集 Validation Set

（2）选择模型

在训练集上训练不同的模型
选择在验证集上错误最小的模型

4、数据稀疏时进行交叉验证 Cross-Validation

将训练集分为S组，每次使用S-1组作为训练集，剩下一组作为验证集
取验证集上平均性能最好的一组

5、模型选择的准则

（1）一些准则

赤池信息量准则 Akaike Information Criterion，AIC
贝叶斯信息准则 Bayesian Information Criterion，BIC

（2）模型复杂度与期望风险之间的关系

偏差-方差分解 Bias-Variance Decomposition

6、偏差-方差分解

（1)期望风险

（2）机器学习能学到的最优模型

（3）期望风险分解

（4）具体方法

bias.x：训练得到的所有模型的期望与最优模型期望的差值的平方，即该模型再不同数据集上得到的平均性能与最优性能的差值
variance.x：在不同数据集上得到的期望与在所有数据集上的平均期望的差值，即该模型对每个数据集上的性能与平均性能之间的差值

（5）期望错误分解

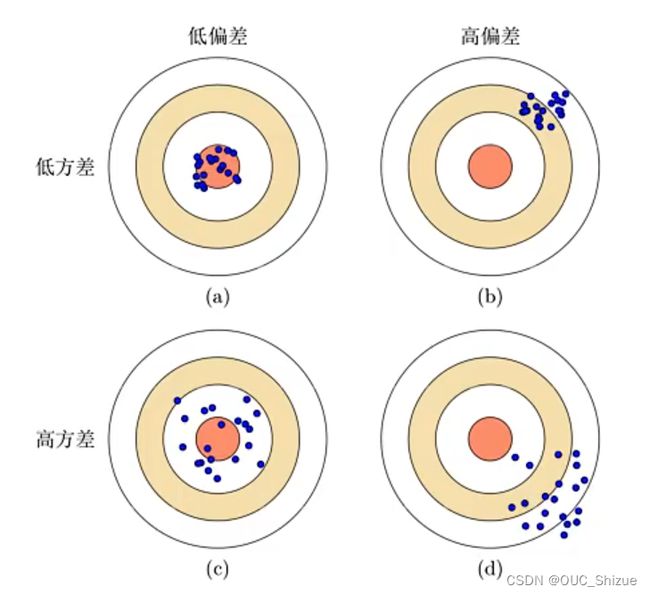
（6）偏差-方差评估模型好坏

每个蓝点表示学习得到的一个模型，越靠近中心效果越好

a表示理想模型
b模型整体能力不够，欠拟合
c模型整体能力不错，但整体较为分散，过拟合；一般通过模型集成来提高模型能力
d模型为失败模型，避免出现

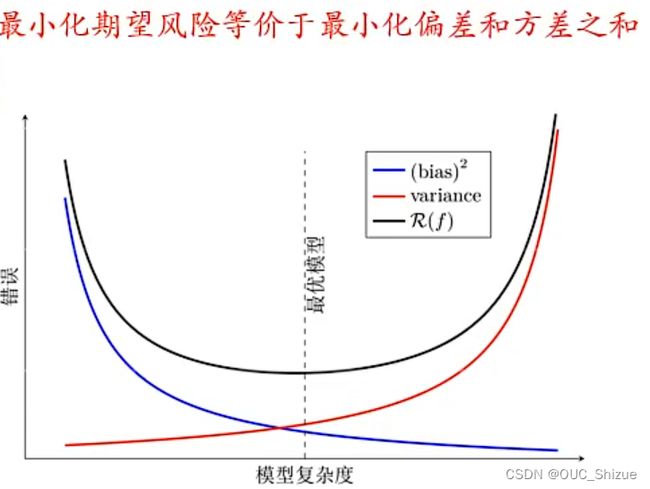
（7）bias、variance、模型复杂度三者关系

注意最优模型并不位于bias与variance交点

八、常用定理

1、没有免费午餐定理 No Free Lunch Theorem，NFL

对于基于迭代的最优算法，不存在某种算法对所有问题都有效

2、丑小鸭定理 Ugly Ducking Theorem

丑小鸭与天鹅之间的区别和两只天鹅之间的区别一样大

3、奥卡姆剃刀原理 Occam’s Razor

如无需要，勿增实体；即可以用简单模型不用复杂模型

4、归纳偏置 Inductive Bias

很多学习算法经常会对学习的问题做一些假设，这些假设就成为归纳偏执

最近邻分类器中，假设在特征空间中，一个小的局部区域中的大部分样本都同属一类
在朴素贝叶斯分类器中，我们会假设每个特征的条件概率是相互独立的
归纳偏置在贝叶斯学习中也常成为先验(Prior)

5、PAC学习

（1）定义

PAC: Probably Approximately Correct，根据大数定律，当训练集大小趋近无穷大时，泛化误差趋向于0，即经验风险趋近于期望风险

（2）样本复杂度计算

第二章：线性模型

一、分类问题示例

二、线性回归模型

1、线性回归模型

2、线性分类模型

由于x连续，而y为离散的label，因此可以在线性f外套一阈值函数，使其离散化。结果表示可以用0/1，+1/-1。
此处的f(x)也称为判别函数 Discriminant Function，g(x)为决策函数
g(f(x;w))为离散模型，但目的是为了在面上画出分类线（或高维内的分类面），因此称为线性分类模型
线性分类模型=线性判别函数+线性决策边界

（1）二分类问题 Binary Classification

学习准则/损失函数：0-1损失函数，即分类正确为1，分类错误为0，但由于该函数无法求导，因此无法对其进行优化

（2）多分类问题 Multi-class Classification

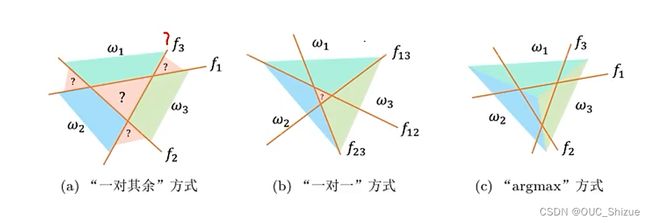
一个超平面无法分解空间，因此需要多条线/面来分割空间；常见模型如下

a模型有多少个类就要建立多少个分类器，产生对应数量的决策面，接着投票；但是会存在问号所示的模糊区域，该类区域不属于任意一个类
b模型两两建立分类器，即有C个类需要建立C(C-1)/2个分类器,但在C较大时所需要的分类器数量较多
c模型对a进行改进，a模型为投票机制，因此会存在模糊区域；而c模型为按得分分类，每个点都属于其中一个类，简单理解为每个点属于其距离最近的类，从而消除了模糊区域

三、交叉熵与对数似然

1、信息论 Information Theory

2、自信息 Self Information

一个随机事件所包含的信息量。对于一个随机变量X，当X=_x_时的自信息_I(x)定义为_I(x)=-log p(x),自信息具有可加性

3、熵 Entropy

（1）熵的信息论定义

信息论中，熵用来衡量一个随机事件的不确定性，例如填词游戏中：applicatio_ 熵小于 appl_，一个事件一定发生则其信息量为0

熵越高，随机变量的信息越多
熵越低，随机变量的信息越少

（2）熵的数学定义

随机变量X的自信息的数学期望称为熵,分布越均衡熵越大

（3）熵编码 Entropy Encoding

在对分布_p(y)_的符号进行编码时，熵_H§_也是理论上最优的平均编码长度，这种编码方式称为熵编码.

例如对一篇文档中的{a,b,c}进行编码，可知其服从某一分布，可根据其自信息设置其码字长度：a的长度为_-log(a)，b的长度为-log(b)，c的长度为-log©，平均码字长度为_H§=-p(a)log(a)-p(b)log(b)-p©log©

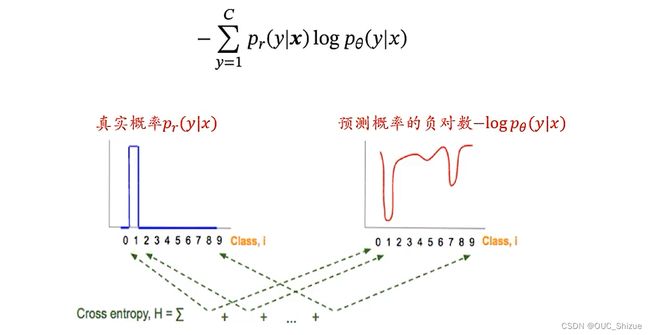
（4）交叉熵 Cross Entropy

可以利用交叉熵来衡量两个分布的差异

（5）KL散度 Kullback-Leibler Divergence

KL散度也可用于衡量两个分布的差异，差异越小KL散度越小，反之越大

4、交叉熵与KL散度应用到机器学习

可以用于衡量真是分布与预测分布之间的差异

由于优化的部分为Pθ，即预测分布，与真实分布Pr无关，因此上式可简化为

因此最小化两个分布的差异，即最小化两个分布的交叉熵；而式中的Pr为one-hot向量形式，因此除_y*项之外均为0，因此可写为_min KL=-logpθ(y*|x)，即负对数似然，因此优化目标转化为使对数似然最大化，即最大对数似然估计

四、Logistic回归 Logistic Regression

1、模型

也称为对数几率回归，简称对率回归，模型如下，其中1为增广向量：

2、分类问题

3、Logistic函数

此类函数也称为Sigmoid函数，其单增且反函数单增，两端饱和，因此常用作神经网络的激活函数，即上述函数g

4、Logistic回归

5、损失函数（学习准则）

由于Logistic回归函数不可导，因此需要将损失函数转化到交叉熵模块，从而进行优化。

（1）定义

（2）梯度下降

五、Softmax回归

Softmax回归可以理解为Logistic回归在多分类问题上的扩展

1、多分类问题 Multi-class Classification

2、Softmax函数

例如：

3、Softmax回归

4、交叉熵损失

例子：

5、学习准则：交叉熵

六、感知器

1、模型

在感知器中y(n)取+1/-1，当y(n)=+1时，如果上式小于0，这说明w*Tx(n)<0，即预测结果为-1，说明预测错误，反之如果上式>0成立则说明预测正确

2、学习算法

每次更新w以后ywTx的值较原值增大，每次更新一个样本，直到所有样本分类正确

3、学习准则

当分类正确时，梯度为0，分类错误时，梯度为-yx

4、感知器的学习过程

每次循环需要对样本重新随机排序，否则靠后的样本对模型的影响会较大，需要进行正则化增大随机性；迭代次数也可通过设置验证集，当模型在验证集上的错误率不再下降时停止迭代。

下图为感知器参数学习的更新迭代过程，分界面为WTx=0：

5、收敛性

七、支持向量机 Support Vector Machine

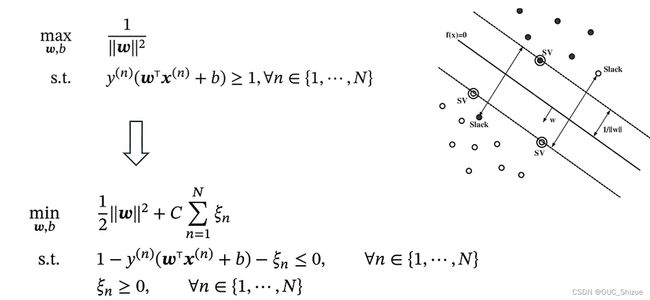
1、最大间隔

2、支持向量机 SVM

3、软间隔 Soft Margin

如果ξ=0则样本线性可分，0<ξ<1说明模型可以分对，但存在部分样本不可分；ξ>1则说明会出现分类错误；因此软间隔SVM的目标为ξ最小

4、带软间隔的支持向量机

可以理解为max部分为经验风险，后项为正则化项，该式也称为Hinge损失函数，感知器损失如下：

对比可见感知器内的点只要分对就不做惩罚，而SVM中即使分对但margin<1仍然要做惩罚

5、SVM优化

约束优化问题，可用拉格朗日优化/KKT算法，可将约束优化转化为非约束优化
SMO算法
梯度下降法

6、SVM优势

可以和核方法（Kernel Method）相结合

八、线性分类模型总结

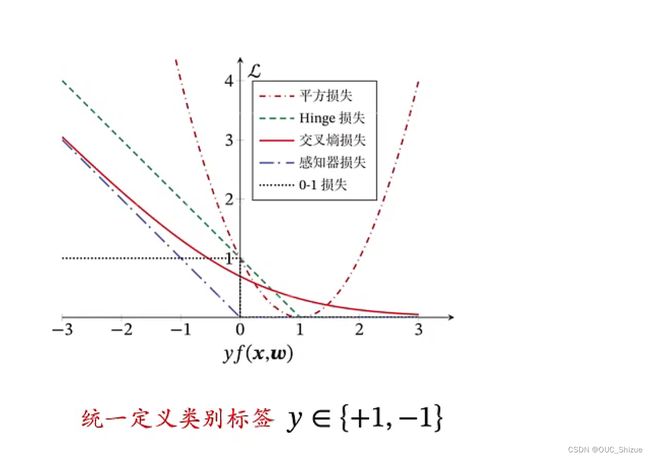
1、不同损失函数的对比

（1）平方损失

从图中可见平方损失在x=1之后上升，说明预测正确依然进行了惩罚，因此平方损失不适合用于分类任务

（2）Logistic回归

随着f(x)的增大对应损失越来越小，符合客观认知，但在f(x)=1之后仍然进行了惩罚，对于分类任务是没有必要的，因此需要再次优化

（3）感知器损失

只要小于0就惩罚，因此适合用感知器进行分类

（4）软间隔SVM损失/Hinge损失

直观理解为感知器向右平移了一个单位，这一个单位用于宽容边界值，小于边界值才进行惩罚

2、小结

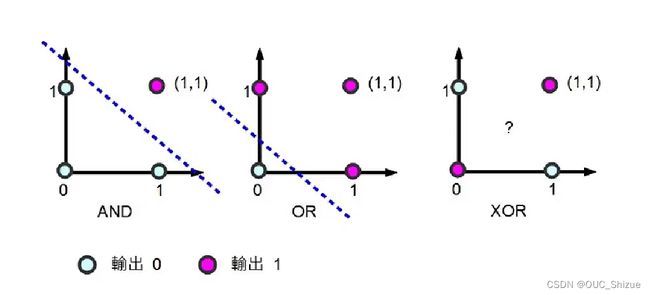
3、线性不可分：XOR问题的解决

(1)问题描述

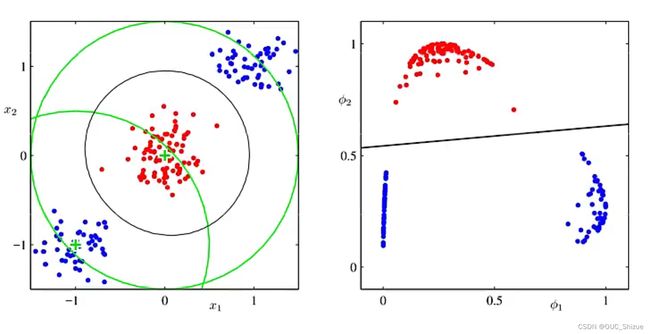
（2）解决方法：使用“基函数”的广义线性模型

例如使用图中一个点作为锚点，然后构造φ(x)计算每个点距离锚点的距离，将两部分点在新的空间构造，从而在新的平面内线性可分

第三章：前馈神经网络（全连接神经网络） FNN

一、神经元

1、激活函数性质

连续并可导（允许少数点上不可导）的非线性函数：可导的激活函数可以直接利用数值优化的方法来学习网络参数
激活函数及其导数要尽可能简单，有利于提高网络计算的效率
激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率及稳定性
总体上升，部分区域可以有波动

2、常用的激活函数

（1）S型函数

相互转化:tanh(x)=2σ(2x)-1
都是饱和函数
Tanh函数是零中心化的，而Logistic函数的输出恒大于0
非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(bias shift)，并进一步使得梯度下降的收敛速度变慢；消除方法为对数据进行归一化；或者加上一个偏置σ(x)+b

（2）斜坡函数

Relu函数

当前机器学习激活函数首选Relu函数，但是存在死亡Relu问题(Dying Relu Problem)，由于ReLU函数左侧为0，因此会出现所有输出都为0的绝对抑制状态，改进方法为使用LeakyReLU(x)函数，即在函数左边让其等于一个很小的参数，从而有了一个小的梯度，保证参数可以更新

LeakyReLU函数

如绿线所示，在x<0时也有一个较小梯度，可以让模型慢慢更新

近似的零中心化非线性函数

Rectifier函数的平滑版本

用曲线去逼近ReLU函数，但是计算相较于ReLU函数复杂，首选仍然是ReLU

Softplus(x)=log(1+exp(x))

（3）复合函数

（1）Swish函数：一种自门控(Self-Gated)激活函数

可以理解为Logistic函数与斜坡函数复合

（2）高斯误差线性单元 Gaussian Error Linear Unit，GELU

高斯分布的累积分布函数也是S形函数，与swish函数类似；但由与高斯分布没有解析解，因此无法直接得到GELU函数，但可以通过Logistic函数与Tanh函数来近似。

3、几种激活函数总结

二、神经网络

1、神经网络三个组成

（1）神经元的激活规则

主要指神经元输入到输出之间的映射关系，一般为非线性函数。

（2）网络的拓扑结构

不同神经元之间的连接关系

（3）学习算法

通过训练数据来学习神经网络的参数

2、连接主义模型

三、前馈神经网络

1、基础概念

各神经元分别属于不同的层，层内无连接
相邻两层之间的神经元全部两两连接
整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示

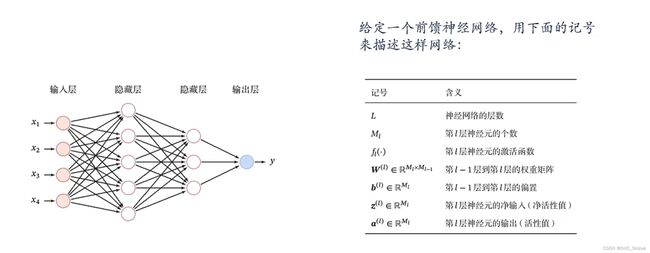
神经网络中输入层为第0层，后续以次为1、2、3…层，其中L M f为超参数，W b为参数，z a为活性值

2、信息传递过程

合并后得到：

前馈计算：

3、通用近似定理

4、应用到机器学习

如果g()为Logistic回归，那么Logistic分类器可看做神经网络的最后一层

5、参数学习

（1）对于多分类问题

（2）结构化风险函数

其中正则化项可以选择Frobenius范数

6、梯度计算方法

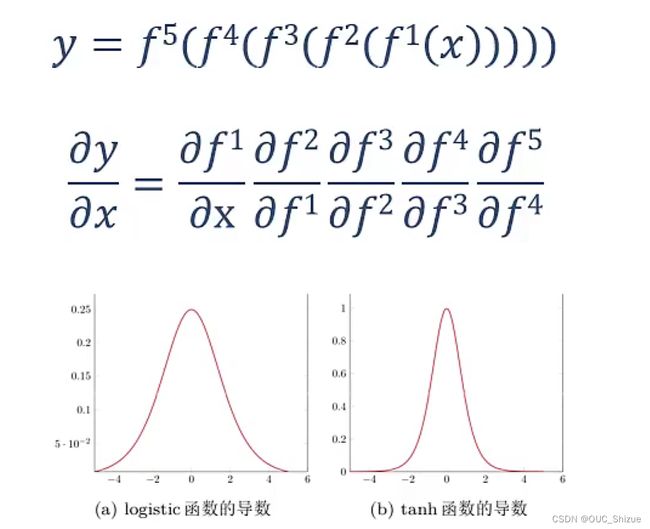
神经网络是一个复杂的复合函数，有以下求解方法：

链式法则求解
反向传播算法（根据前馈网络的特点而设计的高效方法）
自动微分 Automatic Differentiation，AD

四、反向传播算法

1、定义

反向传播(Backpropagation，BP）是误差反向传播的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

2、算法实现

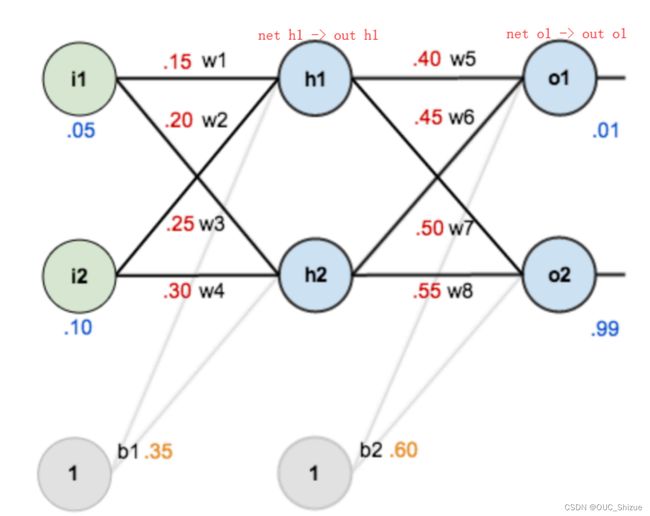
3、实例

（1）网络图

（2）前馈运算激活函数为sigmoid

（3）反向传播

（4）参数更新

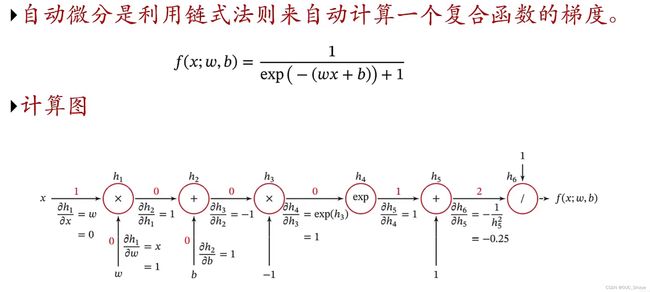
五、计算图与自动微分

1、定义

2、实例

针对上图有：

当x=1，w=0，b=0时，可以得到：

3、前向模式与反向模式

前向模式：传递过程中保存的参数较多，资源消耗可能过大
反向模式：与反向传播相同，资源占用较少

4、静态计算图和动态计算图

静态计算图是在编译时构建计算图，计算图构建成功之后在运行时不能改变，效率较高，可以在构建时进行优化，并行能力强，但灵活性较差（Theano、TensorFlow）
动态计算图在程序运行时动态构建，不容易进行优化，且输入的网络结构不一致时难以进行并行计算，但灵活性较高（DyNet、Chainer、Pytorch）

5、Keras快速搭建神经网络

6、深度学习的三个步骤

定义网络
损失函数
优化

六、前馈神经网络优化

1、非凸优化问题

局部最优但不是全局最优

2、梯度消失问题 Vanishing Gradient Problem

例如导数在0~1之间，连乘以后梯度趋近于0，导致梯度消失，当神经网络深度较深时，下层网络的梯度趋近于0，难以更新；因此激活函数的导数最好在1附近，不能太大或过小，故推荐ReLU函数

3、优化问题难点

非凸优化问题：存在局部最优而非全局最优解，影响迭代
梯度消失问题：下层参数比较难调
参数过多，影响训练，参数解释起来比较困难

4、优化问题需求

计算资源要大
数据要多
算法效率要好，收敛速度快

第四章：卷积神经网络 CNN

一、概述

1、卷积神经网络 Convolutional Neural Networks，CNN

前馈神经网络的一种
受生物学上感受野（Receptive Field）的机制而提出，在视觉神经系统中，一个神经元的感受野是指视网膜上的特定区域，只有这个区域内的刺激才能激活该神经元

2、CNN的三个结构特性

局部连接
权重共享，降低参数数量
空间或时间上的次采样

二、卷积

1、定义

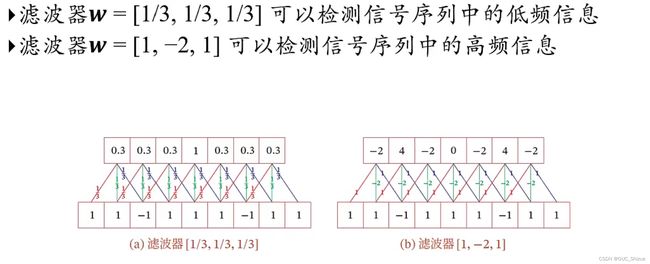
w被称为滤波器（filter）或卷积核（convolution kernel）

如果输入长度为N，滤波器长度为K，则output长度为N-K+1

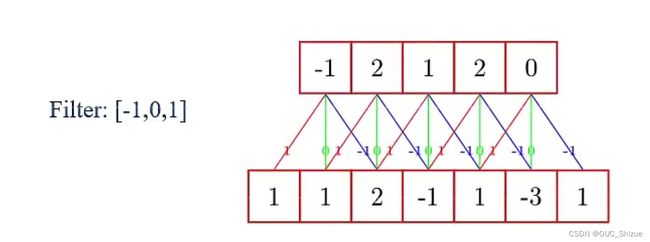
2、举例

此处选用Filter:[-1,0,1]

3、卷积的作用

（1）近似微分

同理，当滤波器w=[1,-2,1]时，可以近似信号序列的二阶微分

（2）低通滤波/高通滤波

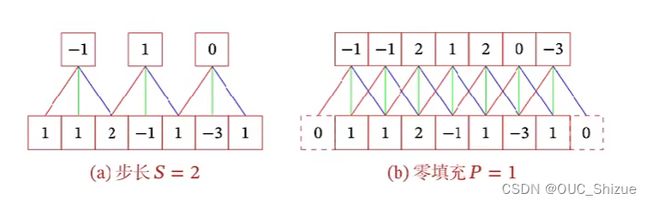
4、卷积扩展

引入滤波器的滑动步长S和零填充P（Padding）

5、卷积类型

（1）按输出长度分类

卷积结果按输出长度不同可以分为三类，在早期文献中，卷积一般默认窄卷积，目前文献中一般默认未等宽卷积

窄卷积，步长S=1，两端不补零P=0，输出长度为M-K+1
宽卷积，S=1，P=K-1，输出长度为M+K-1
等宽卷积，S=1，P=(k-1)/2，输出长度M

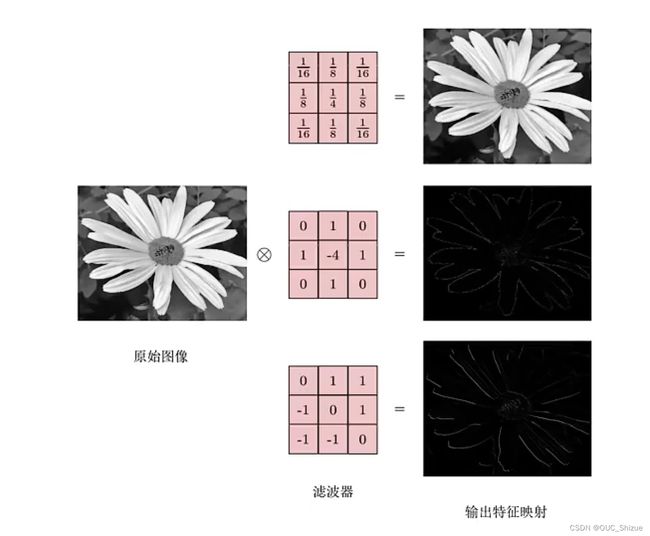
（2）按维数分类

由于图像模块常用二维卷积，因此特别介绍

6、卷积作为特征抽取器

三、卷积神经网络

1、用卷积层代替全连接层

2、互相关

计算卷积需要进行卷积核翻转（但由于w是可学习的参数，因此翻转是非必要的）
卷积操作的目的：提取特征

3、多卷积核

（1）多卷积核目的

将卷积核看做是特征提取器，引入多卷积核可以增强卷积层的能力

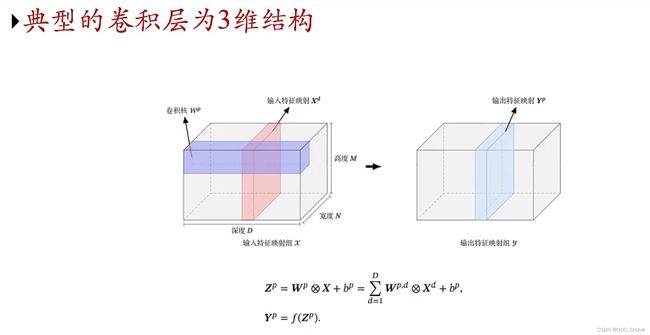
（2）以两维为例

特征映射（Feature Map）：图像经过卷积后得到的特征

卷积层：输入：D个特征映射M×N×D

输出：P个特征映射M’×N’×P

4、卷积层的映射关系

5、卷积层

6、汇聚层 Pooling Layers

7、卷积网络结构

典型结构：

趋向于小卷积、大深度
趋向于全卷积

四、其他卷积类型

1、空洞卷积

（1）如何增加输出单元的感受野

增加卷积核的大小
增加层数
在卷积之前进行汇聚操作

（2）空洞卷积

通过给卷积核插入“空洞”来变相增加其大小

2、转置卷积/微步卷积

五、典型的卷积神经网络

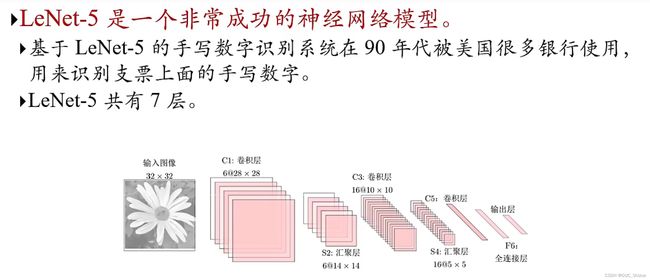
1、LeNet-5

2、Large Scale Visual Recognition Challenge中优秀模型

2015为ResNet

3、AlexNet

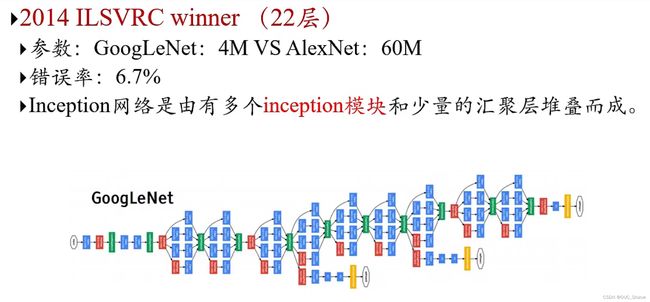
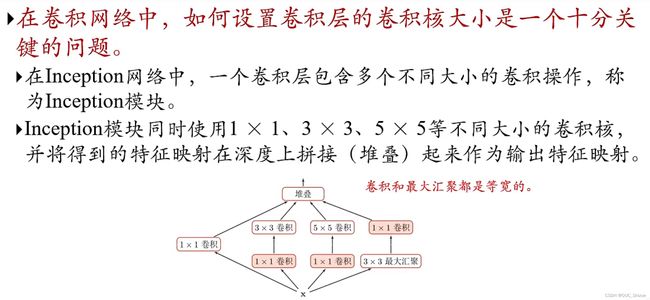
4、Inception网络

（1）Inception模块v1

穷举各类卷积再堆叠，大大提高得到的特征丰富程度

（2）Inception模块v3

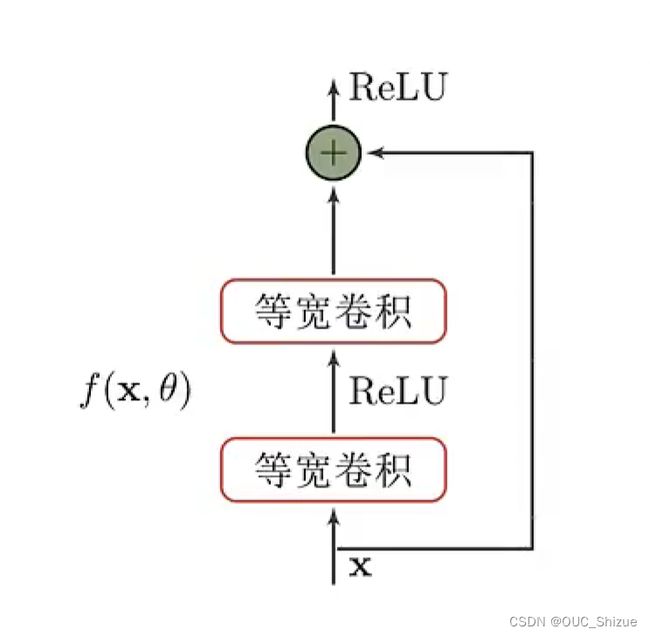
5、残差网络 Residual Network，ResNet

（1）概览

（2）定义

（3）残差单元

（4）残差应用的意义

残差的连接，或者说直连边是深度堆叠必不可少的技术，其使得梯度dh(x)/dx=1+df(x,θ)/dx，由于有1的存在，因此链式法则连乘之后不会出现梯度消失的现象，故可以大量堆叠

六、卷积神经网络的应用

1、AlphaGo

2、目标检测 Object Detection

3、像素级图像分割 RCNN

4、光学识别 OCR

七、卷积应用到文本

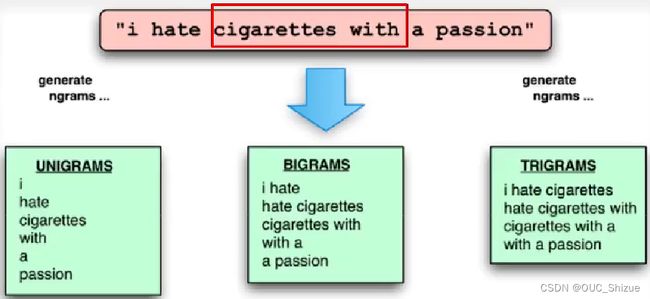
1、Ngram特征与卷积

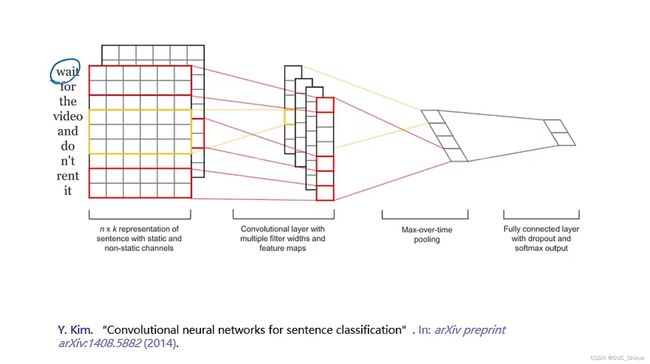
2、基于卷积模型的句子表示

通过查表将单词编程向量

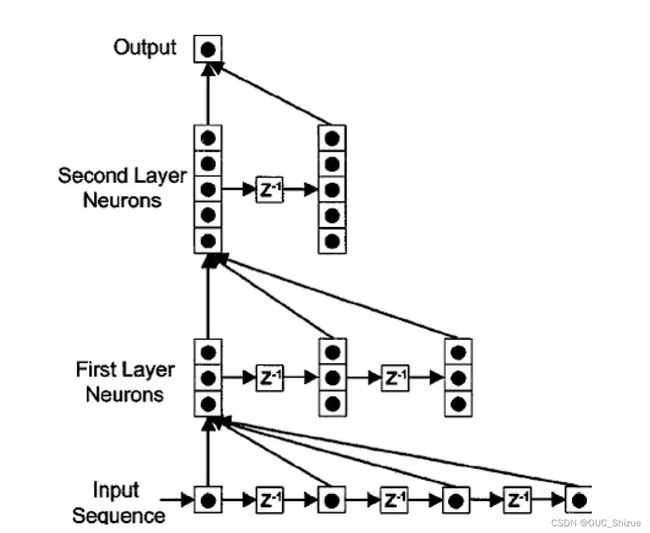
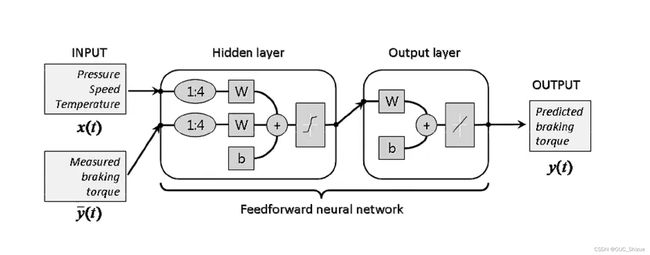
第五章：循环神经网络

一、给前馈神经网络增加记忆力

1、前馈网络特点 FNN

相邻两层之间存在单向连接，层内无连接
构成一个有向简单图
输入和输出的维数是固定的，不能任意改变
（全连接前馈网络）无法处理变长序列数据

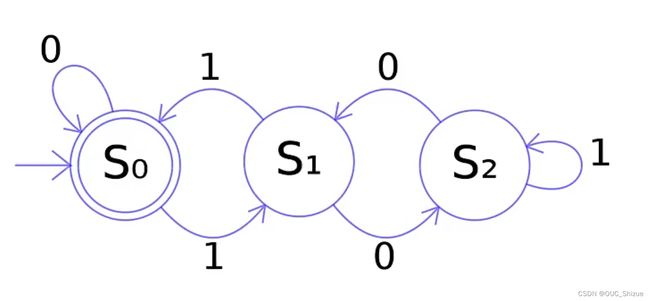
2、有限状态自动机 Finite Automata

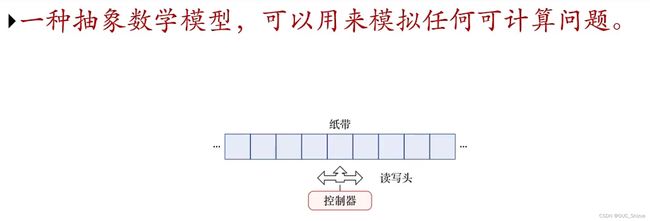
3、图灵机

4、时延神经网络 Time Delay Neural Network，TDNN

5、自回归模型 Autoregressive Model，AR

6、有外部输入的非线性自回归模型 Nonlinear Autoregressive with Exogenous Inputs，NARX

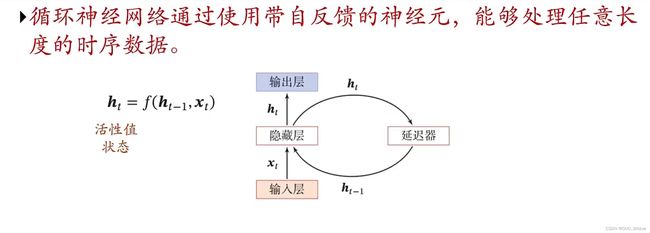
二、循环神经网络 Recurrent Neural Network，RNN

1、图解

RNN比FNN更加符合生物神经网络的结构
RNN已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上

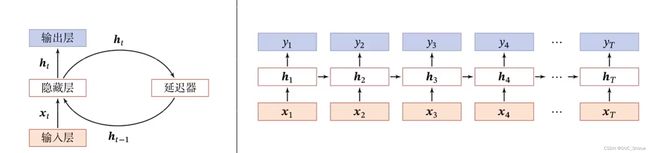
2、按时间展开

时间维度上较浅，需要加深
非时间维上较深，需要考虑梯度消失问题

3、简单循环网络 Simple Recurrent Network，SRN

4、图灵完备 Turing Completeness

5、应用

输入-输出映射（机器学习模型）
存储器（联想记忆模型，例如Hopfield）

三、RNN应用到ML中

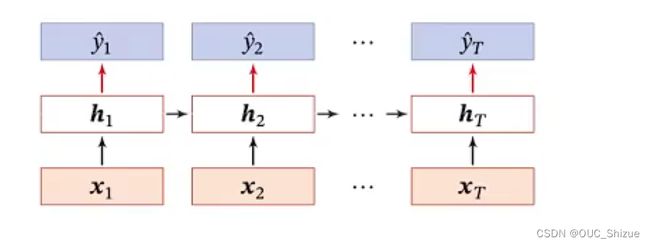
1、序列到类别

输入是个序列（向量），输出是个类别

2、情感分类

第一步要将文字查表映射到一个向量作为一个input

3、同步序列到序列模式

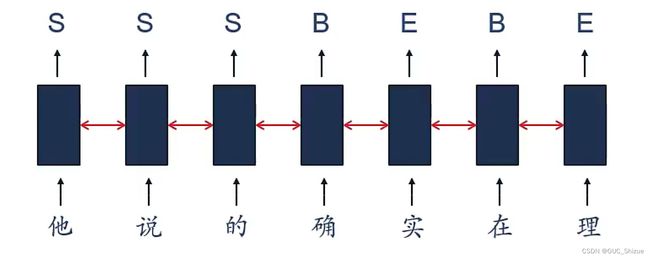
输入是一个序列，输出也是个序列，且是一一对应的

（1）中文分词

（2）信息抽取 Information Extraction，IE

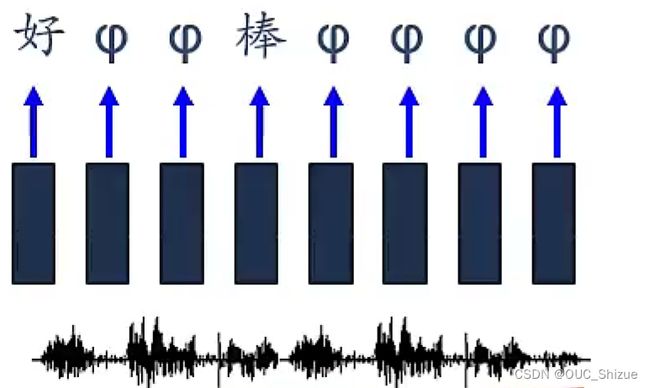
（3）语音识别

Connectionist Temporal Classification，CTC

4、异步序列到序列模式

典型应用为机器翻译

四、参数学习

1、损失函数

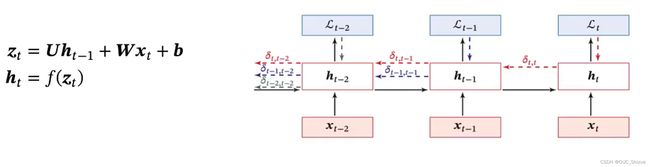
2、随时间反向传播算法 BackPropagation Through Time，BPTT

3、梯度

令括号中的部分等于γ，则

从式子分析，当t-k较大，即两个时间点相隔较远时，若γ>1则梯度->∞，发生梯度爆炸；若γ<1则梯度->0，发生梯度消失

4、长程依赖问题 Long-Term Dependencies Problem

由于梯度爆炸或梯度消失问题，实际上只能学习到短周期的依赖关系；要解决该问题的方法即使得γ=1

五、解决长程依赖问题

1、问题来源

神经网络在时间维度上非常深，容易发生梯度消失或梯度爆炸问题

梯度爆炸可用权重衰减或梯度阶段方法解决；梯度消失则需要改进模型

2、改进方法

循环边改为线性依赖边，但此时ht与ht-1为线性关系，削弱了模型能力

进一步改进，增加非线性

但由于此式子ht一直在增大，当信息饱和时难以更新信息

六、GRU与LSTM

1、门控机制

控制信息的积累速度，包括有选择地加入新的信息，并有选择地遗忘之前累积的信息。

2、门控循环单元 Gated Recurrent Unit，GRU

（1）更新门

Zt为0~1之间的一个一维向量，也称为更新门

（2）重置门

为了实现ht只与xt相关，而与ht-1无关，因此引入重置门

（3）单元实现

3、长短期记忆神经网络 Long Short-Term Memory，LSTM

相较于GRU，其引入了一个内部记忆单元c，用c进行线性传递，将h解放出来，让h专门做非线性，提高模型非线性能力

4、LSRM的变体

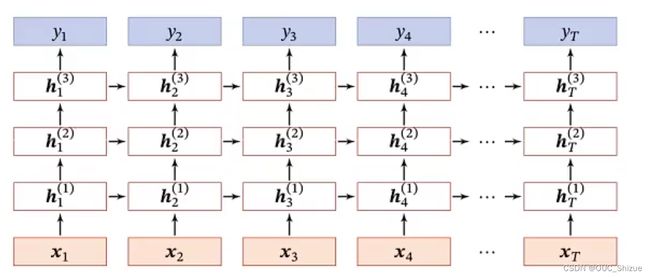
七、深层循环神经网络

1、堆叠循环神经网络

2、双向循环神经网络

3、循环神经网络小结

八、循环神经网络的应用场景

1、语言模型

自然语言理解->一个句子的可能性/合理性，简单理解为对语句进行打分，符合语法又符合语义的给较高分数；因此转化到概率层面，使用RNN解决

（1）N元语言模型

（2）具体实现

2、自动生成Linux内核代码

在Linux上训练一个RNN，让其自动生成内核代码

3、作词机

可以使用某个歌手的全部作品训练RNN，后自动生成歌词

4、机器翻译

（1）传统机器翻译

（2）基于序列到序列的机器翻译

5、看图说话

6、对话系统

九、扩展到图结构

1、树结构

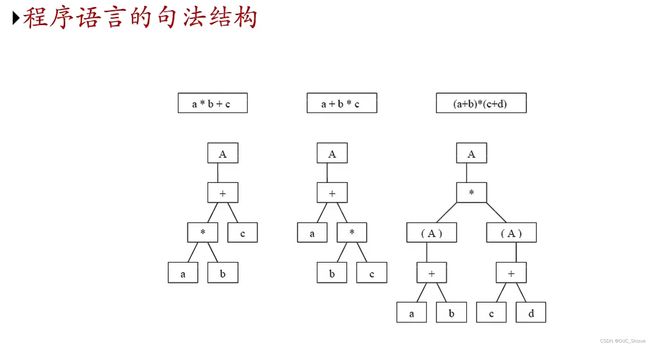
（1）程序

（2）自然语言

2、递归神经网络 Recursive Neural Network

递归神经网络是在一个有向无环图（Tree）上共享一个组合函数

退化为循环神经网络

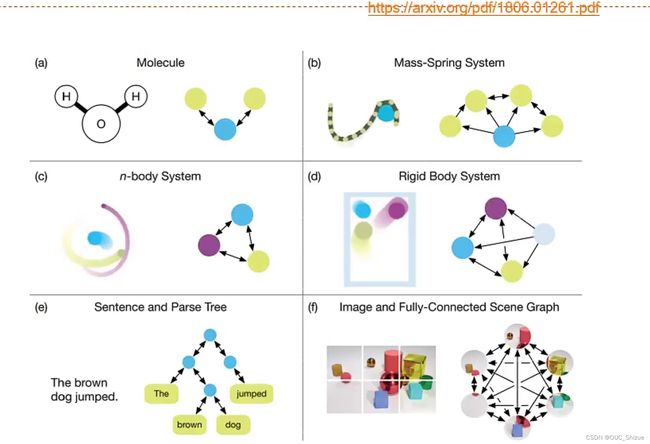
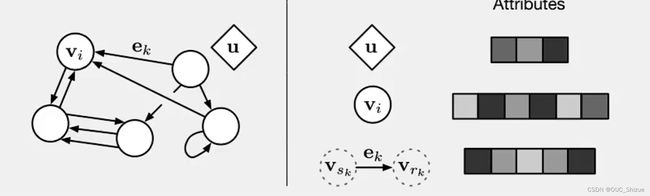
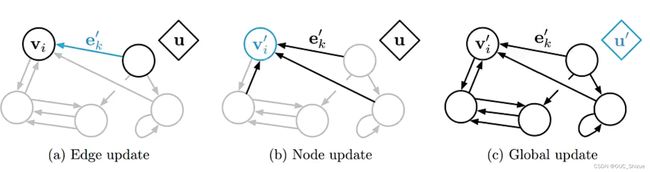
3、图网络（最热门研究方向之一）

（1）图网络举例

（2）构成

（3）图网络更新方式

（4）参数

第六章：网络优化与正则化

一、神经网络优化的特点

1、优化难点

结构差异大

没有通用算法可以适用于所有网络模型

超参数较多
非凸优化问题

参数初始化

逃离局部最优或鞍点
梯度消失/梯度爆炸问题

2、高维空间的非凸优化问题

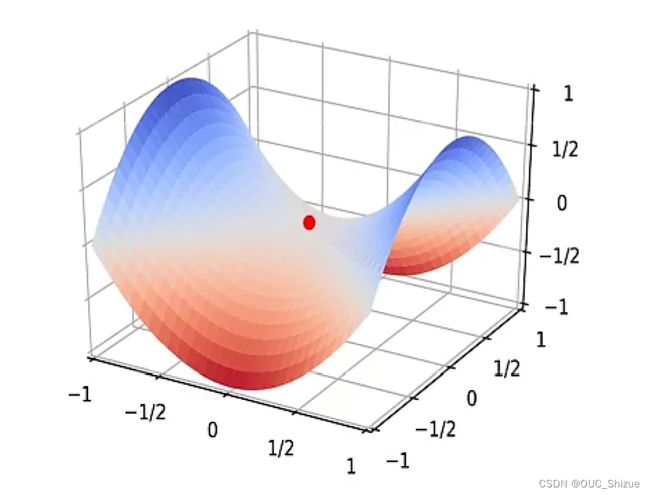
（1）鞍点 Saddle Point

驻点 Stationary Point：梯度为0的点；高维空间中驻点大部分都为鞍点，因此优化重心就为逃离驻点

（2）平坦最小值 Flat Minima

3、优化地形可视化 Optimization Landscape

（1）优化地形：高位空间中损失函数的曲面形状

在没有加入残差连接时地形较为复杂，难以优化

加入残差之后地形光滑

4、神经网络优化的改善方法

更有效的优化算法来提高优化方法的效率和稳定性

动态学习率调整

梯度估计修正

更好的参数初始化方法、数据预处理方法来提高优化效率
修改网络结构来得到更好的优化地形

好的优化地形通常比较平滑

使用ReLU激活函数、残差连接、逐层归一化等

使用更好的超参数优化方法

二、优化算法改进

1、随机梯度下降->小批量随机梯度下降 MiniBatch

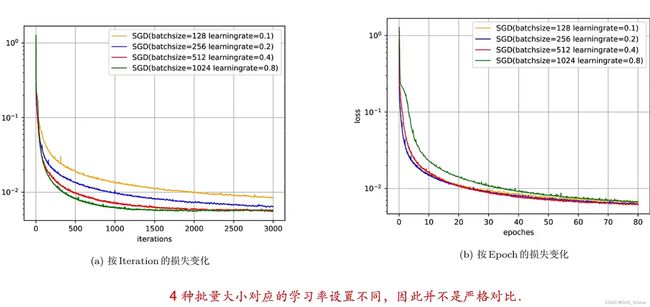
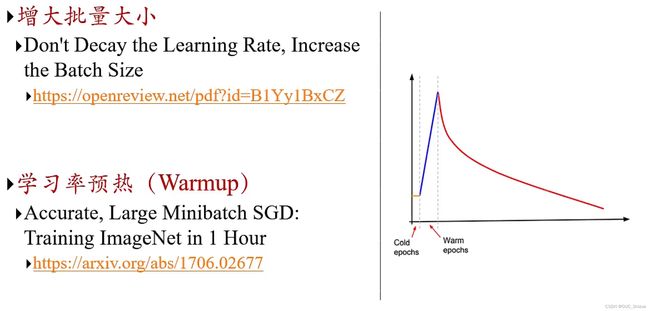
2、批量大小

批量大小不影响随机梯度的期望，但会影响随机梯度的方差

批量越大随机梯度的方差越小，引入噪声越小，训练越稳定，可以设置较大的学习率
批量较小时，需要设置较小的学习率，否则模型会不收敛
批量越大学习率需要越大，即线性缩放规则

3、批量大小对收敛的影响

批量越小随机性越强

4、改进方法

标准的（小批量）梯度下降
学习率

学习率衰减

Adagrad

Adadelta

RMSprop

梯度

Monmentum：计算负梯度的“加权移动平均”作为参数更新的方向

Nesterov accelerated gradient

梯度截断

三、动态学习率

1、学习率的影响

由上图可知，优秀的学习率应该是自适应的，开始大，接近最优点时逐步减小

2、学习率衰减

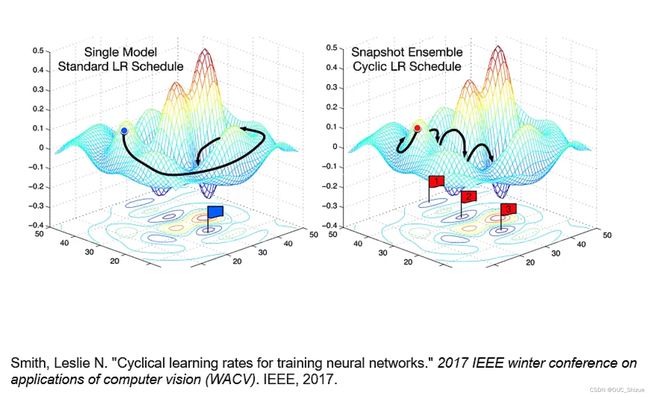
3、周期性学习率调整 Cyclical Learning Rates

目的是跳出局部最优

4、其他学习率调整方法

5、自适应学习率

根据梯度动态计算当前学习率

四、梯度方向优化

1、动量法 Momentum Method

用之前累积的动量来替代真正的梯度

负梯度的加权移动平均

每次迭代的梯度可以看做是加速度，可以近似看做二阶梯度

2、Nesterov加速梯度

3、Adam算法≈动量法+RMSprop

4、几种算法速度对比

5、梯度截断

6、优化算法改进小结

五、参数初始化

1、对称权重问题

参数初始化为0导致神经元行为都一致。

2、初始化方法

预训练初始化
随机初始化
固定值初始化（bias通常用0来初始化）

3、随机初始化

（1）Gaussian分布初始化

该初始化为最简单的初始化方法，参数从一个固定均值（比如0）和固定方差（比如0.01）的Gaussian分布进行初始化。

（2）均匀分布初始化

参数可以在区间[-r,r]内采用均匀分布进行初始化。

（3）范数保持性 Norm-Preserving

可以基于方差缩放的参数初始化；或正交初始化

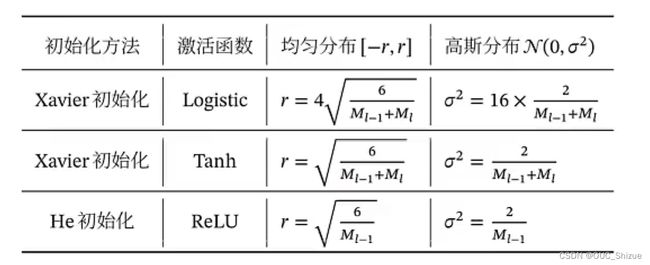
4、基于方差缩放的参数初始化

Xavier初始化和He初始化

5、正交初始化 Orthogonal Initialization

方法：

用均值为0、方差为1的高斯分布初始化一个矩阵
将这个矩阵用奇异值分解得到两个正交矩阵，使用其中一个作为权重矩阵

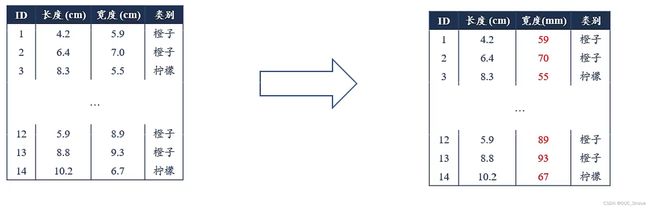
六、数据预处理

1、尺度不变性 Scale Invariance

机器学习算法在缩放全部或部分特征后不影响学习和预测

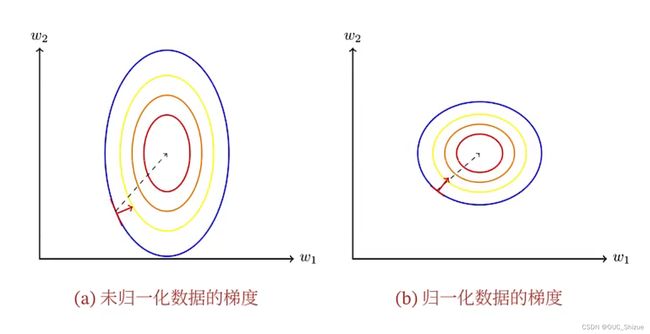
2、数据规范对梯度的影响

3、规范化 Normalization

七、逐层规范化

1、目的

更好的尺度不变性：内部协变量偏移
更平滑的优化地形

2、规范化方法

批量规范化 Batch Normalization，BN

层规范化 Layer Normalization

权重规范化 Weight Normalization

局部响应规范化 Local Response Normalization，LRN

3、批量规范化

4、批量规范化

八、超参数优化

1、常见超参

层数
每层神经元数量
激活函数
学习率（以及动态调整算法）
正则化系数
mini-batch大小

2、优化方法

网格搜索
随机搜索
贝叶斯优化
动态资源分配
神经架构搜索

3、网格搜索 Grid Search

九、网格正则化

1、正则化 Regularization

2、如何提高神经网络的泛化能力

（1）干扰优化过程

早停法 Early-Stop
暂退法 Dropout
权重衰减
SGD

（2）增加约束

l1和l2正则化
数据增强

3、早停法 Early-Stop

引入一个验证集validation Dataset来测试每一次迭代的参数在验证集上是否最优，如果在验证集上错误率不再下降就停止迭代

4、权重衰减 Weight Decay

通过限制权重的取值范围来干扰优化过程，降低模型能力
在每次参数更新时，引入一个衰减系数β

十、暂退法 Dropout Method

1、概念及其原理

2、dropout意义

（1）集成学习的解释

每做一次暂退，相当于从原始网络中采样得到一个子网络。如一个神经元有n个神经元，那么总共可以采样出2^n个子网络