Pytorch梯度下降优化

目录

一、激活函数

1.Sigmoid函数 

2.Tanh函数

3.ReLU函数

二、损失函数及求导

1.autograd.grad

2.loss.backward()

3.softmax及其求导

三、链式法则

1.单层感知机梯度

2. 多输出感知机梯度

3. 中间有隐藏层的求导

4.多层感知机的反向传播

四、优化举例

---

一、激活函数

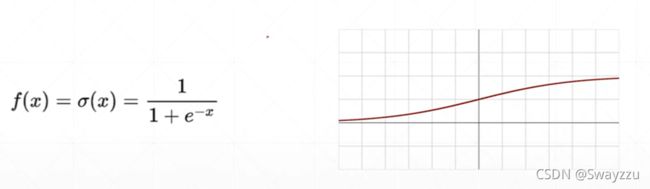
1.Sigmoid函数 

函数图像以及表达式如下：

通过该函数，可以将输入的负无穷到正无穷的输入压缩到0-1之间。在x=0的时候，输出0.5

通过PyTorch实现方式如下：

2.Tanh函数

在RNN中比较常用，由sigmoid函数变化而来。表达式以及图像如下图所示：

该函数的取值是-1到1，导数是：1-Tanh**2。

通过PyTorch的实现方式如下：

3.ReLU函数

该函数可以将输入小于0的值截断为0，大于0的值保持不变。因此在小于0的地方导数为0，大于0的地方导数为1，因此求导计算非常方便。

通过PyTorch的实现方式如下：

 

二、损失函数及求导

通常，我们使用mean squared error也就是均方误差来作为损失函数。

1.autograd.grad

torch.autograd.grad(loss, [w1,w2,...])

输入的第一个是损失函数，第二个是参数的列表，即使只有一个，也需要加上中括号。

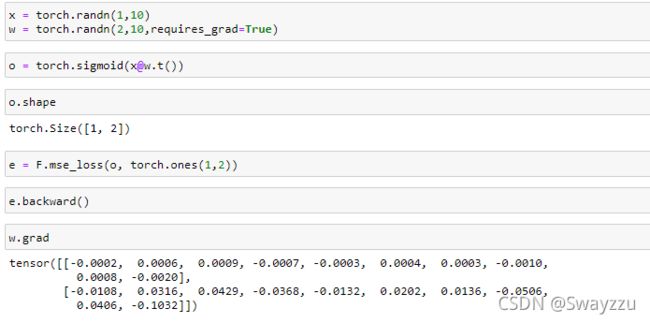
 我们可以直接通过mse_loss的方法，来直接创建损失函数。

在torch.autograd.grad中输入损失函数mse，以及希望求导的对象[w]，可以直接求导。

注意：我们需要在创建w的时候，需要添加requires_grad=True，我们才能对它求导。

也可以通过w.requires_grad_()的方法，为其添加可以求导的属性。

2.loss.backward()

该方法是直接在损失函数上面调用的

这个方法不会返回梯度信息，而是将梯度信息保存到了参数中，直接用w.grad就可以查看。 

3.softmax及其求导

该函数将差距较大的输入，转换成处于0-1之间的概率，并且所有概率和为1。

 对softmax函数的求导：

设输入是a，通过了softmax输出的是p

注意：当i=j时，偏导是正的，i != j时，偏导是负的。

通过PyTorch实现方式如下：

三、链式法则

1.单层感知机梯度

单层感知机其实就是只有一个节点，数据*权重，输入这个节点，经过sigmoid函数转换，得到输出值。根据链式法则可以求得梯度。

 通过PyTorch可以轻松实现函数转换以及求导。

2. 多输出感知机梯度

输出值变多了，因此节点变多了。但求导方式其实是一样的。

 通过PyTorch实现求导的方式如下：

3. 中间有隐藏层的求导

中间加了隐藏层，只是调节了输出节点的输入内容。原本是数据直接输给输出节点，现在是中间层的输出作为输入，给了输出节点。使用PyTorch实现方式如下：

4.多层感知机的反向传播

依旧是通过链式法则，每一个结点的输出sigmoid(x)都是下一个结点的输入，因此我们通过前向传播得到每一个结点的sigmoid函数，以及最终的输出结果，算出损失函数后，即可通过后向传播依次推算出每一个结点每一个参数的梯度。

下面的DELTA(k)只是将一部分内容统一写作一个字母来表示，具体推导不再详述。

四、优化举例

通过以下函数进行优化。

 优化流程：初始化参数→前向传播算出预测值→得到损失函数→​​​​​​​反向传播得到梯度→​​​​​​​对参数更新→​​​​​​​再次前向传播→......

在此案例中，优化流程有一些不同：

优化之前先选择优化器，并直接把参数，以及梯度输入进去。

①pred = f(x)根据函数给出预测值，用以后面计算梯度。

②optimizer.zero_grad()梯度归零。因为反向传播之后，梯度会自动带到参数上去（上面有展示，可以调用查看）。

③pred.backward()用预测值计算梯度。

④pred.step()更新参数。

以上步骤循环即可。