数组和矩阵问题
文章目录
-
- 转圈打印矩阵
- 将正方形矩阵顺时针转动 90°
- “之”字形打印矩阵
- 找到无序数组中最小的 k 个数
- 需要排序的最短子数组长度
- 在数组中找到出现次数大于 N/K 的数
- 在行列都排好序的矩阵中找指定数
- 最长的可整合子数组的长度
- 不重复打印排序数组中相加和为给定值的所有二元组和三元组
- 未排序正数数组中累加和为给定值的最长子数组长度
- 未排序数组中累加和为给定值的最长子数组系列问题
- 未排序数组中累加和小于或等于给定值的最长子数组长度
- 计算数组的小和
- 自然数数组的排序
- 奇数下标都是奇数或者偶数下标都是偶数
- 子数组的最大累加和问题
- 子矩阵的最大累加和问题
- 在数组中找到一个局部最小的位置
- 数组中子数组的最大累乘积
- 打印 N 个数组整体最大的 Top K
- 边界都是 1 的最大正方形大小
- 不包含本位置值的累乘数组
- 数组的 partition 调整
- 求最短通路值
- 数组中未出现的最小正整数
- 数组排序之后相邻数的最大差值
- 做项目的最大收益问题
- 分金条的最小花费
- 大楼轮廓问题
- 加油站良好出发点问题
- 容器盛水问题
说明:本文将《程序员代码面试指南(第2版)》的数组和矩阵问题部分以C++形式呈现(原文为JAVA版)。由于本人为C++萌新(只学了一点点基础语法),代码中有诸多不规范之处请读者谅解。是为练手之作,但所写代码均可正确运行(只要按照代码要求输入……有一说一,我的这个输入有点一言难尽,但是水平就到这儿了,QAQ)。
转圈打印矩阵
【题目】
给定一个整型矩阵 matrix,请按照转圈的方式打印它。
例如:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
打印结果为:1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10
【解答】
-
矩阵分圈处理
在矩阵中用左上角的坐标(tR,tC)和右下角的坐标(dR,dC)就可以表示一个子矩阵,比如题目中的矩阵,当(tR,tC)=(0,0)、(dR,dC)=(3,3)时,表示的子矩阵就是整个矩阵,那么这个子矩阵最外层的部分如下:
1 2 3 4
5 8
9 12
13 14 15 16
如果能把这个子矩阵的外层转圈打印出来,那么在(tR,tC)=(0,0)、(dR,dC)=(3,3)时,打印的结果为:1,2,3,4,8,12,16,15,14,13,9,5。
接下来令 tR 和 tC 加 1,即(tR,tC)=(1,1), 令 dR 和 dC 减 1,即(dR,dC)=(2,2),此时表示的子矩阵如下:
6 7
10 11
再把这个子矩阵转圈打印出来,结果为:6,7,11,10。
把 tR 和 tC 加 1,即(tR,tC)=(2,2), 令 dR 和 dC 减 1,即(dR,dC)=(1,1)。发现左上角坐标跑到了右下角坐标的右方或下方,整个过程就停止。已经打印的所有结果连起来就是我们要求的打印结果。
【代码】
#include 将正方形矩阵顺时针转动 90°
【题目】
给定一个 N×N 的矩阵 matrix,把这个矩阵调整成顺时针转动 90°后的形式。
例如:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
顺时针转动 90°后为:
13 9 5 1
14 10 6 2
15 11 7 3
16 12 8 4
【解答】
-
矩阵分圈处理
在矩阵中用左上角的坐标(tR,tC)和右下角的坐标(dR,dC)就可以表示一个子矩阵。比如题目中的矩阵,当(tR,tC)=(0,0)、(dR,dC)=(3,3)时,表示的子矩阵就是整个矩阵,那么这个子矩阵最外层的部分如下:
1 2 3 4
5 8
9 12
13 14 15 16
在这个外圈中,1,4,16,13 为一组,然后让 1 占据 4 的位置,4 占据 16 的位置,16 占据 13 的位置,13 占据 1 的位置,一组就调整完了。
然后 2,8,15,9 为一组,继续占据调整的过程,最后 3,12,14,5 为一组,继续占据调整的过程。
(tR,tC)=(0,0)、(dR,dC)=(3,3)的子矩阵外层调整完毕。接下来令 tR 和 tC 加 1,即(tR,tC)=(1,1),令 dR 和 dC 减 1,即(dR,dC)=(2,2),此时表示的子矩阵如下:
6 7
10 11
这个外层只有一组,就是 6,7,11,10,占据调整之后即可。所以,如果子矩阵的大小是M×M,一共就有 M-1 组,分别进行占据调整即可。
【代码】
#include “之”字形打印矩阵
【题目】
给定一个矩阵 matrix,按照“之”字形的方式打印这个矩阵。
例如:
1 2 3 4
5 6 7 8
9 10 11 12
“之”字形打印的结果为:1,2,5,9,6,3,4,7,10,11,8,12。
【解答】
-
矩阵斜线处理
1.上坐标(tR,tC)初始为(0,0),先沿着矩阵第一行移动(tC++),当到达第一行最右边的元素后,再沿着矩阵最后一列移动(tR++)。
2.下坐标(dR,dC)初始为(0,0),先沿着矩阵第一列移动(dR++),当到达第一列最下边的元素时,再沿着矩阵最后一行移动(dC++)。
3.上坐标与下坐标同步移动,每次移动后的上坐标与下坐标的连线就是矩阵中的一条斜线,打印斜线上的元素即可。
4.如果上次斜线是从左下向右上打印的,这次一定是从右上向左下打印,反之亦然。总之,可以把打印的方向用 bool 值表示,每次取反即可。
【代码】
#include 找到无序数组中最小的 k 个数
【题目】
给定一个无序的整型数组 arr,找到其中最小的 k 个数。
【解答】
-
法一:堆排(O(Nlogk))
一直维护一个有 k 个数的大根堆,这个堆代表目前选出的 k 个最小的数,在堆里的 k 个元素中,堆顶的元素是最小的 k 个数里最大的那个。 接下来遍历整个数组,遍历的过程中看当前数是否比堆顶元素小。如果是,就把堆顶的元素替换成当前的数,然后从堆顶的位置调整整个堆,让替换操作后堆的最大元素继续处在堆顶的位置;如果不是,则不进行任何操作,继续遍历下一个数;在遍历完成后,堆中的 k 个数就是所有数组中最小的 k 个数。
【代码】
- 法一:自定义堆
#include - 法一:调用优先队列作为大根堆
#include -
法二:BFPRT算法(O(N))
BFPRT 算法解决了这样一个问题,在时间复杂度 O(N)内,从无序的数组中找到第 k 小的数。假设 BFPRT 算法的函数是 int select(vector arr, int k),该函数的功能为在 arr 中找到第 k 小的数,然后返回该数。select(arr, k)的过程如下:
1.将 arr 中的 n 个元素划分成 n/5 组,每组 5 个元素,如果最后的组不够 5 个元素,那么最后剩下的元素为一组(n%5 个元素)。
2.对每个组进行插入排序,只针对每个组最多 5 个元素之间的组内排序,组与组之间并不排序。排序后找到每个组的中位数,如果组的元素个数为偶数,这里规定找到下中位数。
3.步骤 2 中一共会找到 n/5 个中位数,让这些中位数组成一个新的数组,记为 mArr。递归调用 select(mArr,mArr.size()/2) ,意义是找mArr 数组中的中位数,即 mArr 中第 (mArr.size()/2)小的数。
4.假设步骤 3 中递归调用 select(mArr,mArr.size()/2)后,返回的数为 x。根据这个 x 划分整个 arr 数组(partition 过程),划分的过程为:在 arr 中,比 x 小的数都在 x 的左边,大于 x 的数都在 x 的右边,x 在中间。划分完成后,x 在 arr 中的位置记为 i。
5.如果 i==k,说明 x 为整个数组中第 k 小的数,直接返回。
- 如果 i
- 如果 i>k,说明 x 处在第 k 小的数的右边,应该在 x 的左边寻找第 k 小的数,所以递归调用 select 函数,在左半区寻找第 k 小的数。
- 如果 i
-
在以下代码实现中,对于当中位数的中位数 x 在 arr 中大量出现的情况做了优化,即返回在通过 x 划分 arr 后,等于 x 的整个位置区间。比如,pivotRange=[a,b]表示 arr[a…b]上都是 x,并以此区间去命中第 k 小的数,如果在[a,b]上,就是命中,如果没在[a,b]上,表示没命中。这样既可以尽量少地进行递归过程,又可以增加淘汰的数据量,使得步骤 5 的递归过程变得数据量更少。
【代码】
- 法二
#include 需要排序的最短子数组长度
【题目】
给定一个无序数组 arr,求出需要排序的最短子数组长度。 例如:arr = [1,5,3,4,2,6,7]返回 4,因为只有[5,3,4,2]需要排序。
【解答】
-
从右向左,从左向右两次遍历确定左右两边界
初始化变量 noMinIndex=-1,从右向左遍历,遍历的过程中记录右侧出现过的数的最小值,记为 minValue。假设当前数为 arr[i],如果 arr[i]>minValue,说明如果要整体有序,minValue 值必然会挪到arr[i] 的左边。用 noMinIndex 记录最左边出现这种情况的位置。如果遍历完成后,noMinIndex 依然等于-1,说明从右到左始终不升序,原数组本来就有序,直接返回 0,即完全不需要排序。
接下来从左向右遍历,遍历的过程中记录左侧出现过的数的最大值,记为 maxValue。假设当前数为 arr[i],如果 arr[i]
遍历完成后,arr[noMinIndex…noMaxIndex]是真正需要排序的部分,返回它的长度即可。
【代码】
#include 在数组中找到出现次数大于 N/K 的数
【题目】
给定一个整型数组 arr,再给定一个整数 K,打印所有出现次数大于 N/K 的数, 如果没有这样的数,打印提示信息。
【解答】
-
将互不相同的数分到一组然后删除
核心思路是,一次在数组中删掉 K 个不同的数,不停地删除,直到剩下数的种类不足 K 就停止删除,那么,如果一个数在数组中出现的次数大于 N/K,则这个数最后一定会被剩下来(想象成N%K)。
只要立 K-1 个候选,然后有 K-1 个 times统计即可,具体过程如下。
遍历到 arr[i]时,看 arr[i]是否与已经被选出的某一个候选相同。如果与某一个候选相同,就把属于那个候选的点数统计加 1。
如果与所有的候选都不相同,先看当前的候选是否选满了,K-1 就是满,否则就是不满:
-
如果不满,把 arr[i]作为一个新的候选,属于它的点数初始化为 1。
-
如果已满,说明此时发现了 K 个不同的数,arr[i]就是第 K 个。此时把每一个候选各自的点数全部减 1,表示每个候选“付出”一个自己的点数。如果某些候选的点数在减1 之后等于 0,则还需要把这些候选都删除,候选又变成不满的状态。
在遍历过程结束后,再遍历一次 arr,验证被选出来的所有候选有哪些出现次数真的大于 N/K,打印符合条件的候选。
-
【代码】
#include 附:
对于出现次数大于一半的数(即N/K=N/2,K=2),最多只会有一个,还可能不存在这样的数。具体的过程为,一次在数组中删掉两个不同的数,不停地删除,直到剩下的数只有一种(如果存在出现次数大于一半的数,就相当于用这个数与其他数两两消去,最后只剩下这个数),再进行判断。
【代码】
#include 在行列都排好序的矩阵中找指定数
【题目】
给定一个 N×M 的整型矩阵 matrix 和一个整数 K,matrix 的每一行和每一列都是排好序的。实现一个函数,判断 K 是否在 matrix 中。
例如:
0 1 2 5
2 3 4 7
4 4 4 8
5 7 7 9
如果 K 为 7,返回 true;如果 K 为 6,返回 false。
【解答】
-
挑选合适的遍历的起点
若K
若K>matrix[row] [col],则K只可能在[row,col]的右下方,锁定右下方区域即否定了(后面就不考虑)其他3块(包括左上,右上,左下)所有区域。
步骤如下:
1.从矩阵最右上角的数开始寻找(row=0,col=M-1)。
2.比较当前数 matrix[row] [col]与 K 的关系:
-
如果与 K 相等,说明已找到,直接返回 true。
-
如果比 K 大,因为矩阵每一列都已排好序,所以在当前数所在的列中,处于当前数下方的数都会比 K 大,则没有必要继续在第 col 列上寻找,令 col=col-1,重复步骤 2。
-
如果比 K 小,因为矩阵每一行都已排好序,所以在当前数所在的行中,处于当前数左方的数都会比 K 小,则没有必要继续在第 row 行上寻找,令 row=row+1,重复步骤 2。
即每次循环初始[row,col]都相当于有效子矩阵的右上角。
3.如果找到越界都没有发现与 K 相等的数,则返回 false。
或者,也可以用以下步骤:
1.从矩阵最左下角的数开始寻找(row=N-1,col=0)。
2.比较当前数 matrix[row] [col]与 K 的关系:
-
如果与 K 相等,说明已找到,直接返回 true。
-
如果比 K 大,因为矩阵每一行都已排好序,所以在当前数所在的行中,处于当前数右方的数都会比 K 大,则没有必要继续在第 row 行上寻找,令 row=row-1,重复步骤 2。
-
如果比 K 小,因为矩阵每一列都已排好序,所以在当前数所在的列中,处于当前数上方的数都会比 K 小,则没有必要继续在第 col 列上寻找,令 col=col+1,重复步骤 2。
3.如果找到越界都没有发现与 K 相等的数,则返回 false。
-
【代码】
#include
// }else{
// cout<<"false"<
// }
cout << boolalpha << flag << endl;
system("pause");
return 0;
}
最长的可整合子数组的长度
【题目】
先给出可整合数组的定义:如果一个数组在排序之后,每相邻两个数差的绝对值都为 1,则该数组为可整合数组。例如,[5,3,4,6,2]排序之后为[2,3,4,5,6],符合每相邻两个数差的绝对值都为 1,所以这个数组为可整合数组。
给定一个整型数组 arr,请返回其中最大可整合子数组的长度。例如,[5,5,3,2,6,4,3]的最大可整合子数组为[5,3,2,6,4],所以返回 5。
【解答】
-
通过特征规律找途径(方向由找个别差异性转为找整体共性)
对 arr 中的每一个子数组 arr[i…j](0≤i≤j≤N-1),都验证一下是否符合可整合数组的定义。
这里时间复杂度高但容易理解的做法是:对 arr[i…j]排序,看是否依次递增且每次递增 1。
然后在所有符合可整合数组定义的子数组中,记录最大的那个长度,返回即可。
但是验证可整合数组真的需要如此麻烦吗?有没有更好的方法来加速验证过程?
判断一个数组是否是可整合数组还可以用以下方法:一个数组中如果没有重复元素,并且最大值减去最小值,再加 1 的结果等于元素个数(max−min+1=元素个数),那么这个数组就是可整合数组。比如[3,2,5,6,4],max−min+1=6-2+1=5=元素个数,所以这个数组是可整合数组。
【代码】
#include 不重复打印排序数组中相加和为给定值的所有二元组和三元组
【题目】
二元组:给定排序数组 arr 和整数 k,不重复打印 arr 中所有相加和为 k 的不降序二元组。
例如,arr=[-8,-4,-3,0,1,2,4,5,8,9],k=10,打印结果为:
1,9
2,8
三元组:给定排序数组 arr 和整数 k,不重复打印 arr 中所有相加和为 k 的不降序三元组。
例如,arr=[-8,-4,-3,0,1,2,4,5,8,9],k=10,打印结果为:
-4,5,9
-3,4,9
-3,5,8
0,1,9
0,2,8
1,4,5
【解答】
-
二元组:双指针
利用排序后数组的特点,打印二元组的过程可以用一个左指针和一个右指针不断向中间压缩的方式实现,具体过程为:
1.设置变量 left=0,right=arr.size()-1。
2.比较 arr[left]+arr[right]的值(sum)与 k 的大小:
-
如果 sum 等于 k,打印“arr[left],arr[right]”,则 left++,right–。
-
如果 sum 大于 k,right–。
-
如果 sum 小于 k,left++。
3.如果 left
那么如何保证不重复打印相同的二元组呢?只需在打印时增加一个检查即可,检查 arr[left]是否与它前一个值 arr[left-1]相等,如果相等,就不打印。具体解释为:因为整体过程是从两头向中间压缩的过程,如果 arr[left]+arr[right]=k,又有 arr[left]=arr[left-1],那么之前一定已经打印过这个二元组,此时无须重复打印。比如 arr=[1,1,1,9],k=10。首先打印 arr[0]和 arr[3]的组合,接下来就不再重复打印 1 和 9 这个二元组。
-
-
三元组:调用二元组
三元组的问题类似于二元组的求解过程。
例如: arr=[-8,-4,-3,0,1,2,4,5,8,9],k=10。
- 当三元组的第一个值为-8 时,寻找-8 后面的子数组中所有相加为 18 的不重复二元组。
- 当三元组的第一个值为-4 时,寻找-4 后面的子数组中所有相加为 14 的不重复二元组。
- 当三元组的第一个值为-3 时,寻找-3 后面的子数组中所有相加为 13 的不重复二元组。
依此类推。
如何不重复打印相同的三元组呢?首先要保证每次寻找过程开始前,选定的三元组中第一个值不重复,其次就是和二元组的打印检查一样,要保证不重复打印二元组。
【代码】
- 二元组
#include - 三元组
#include 未排序正数数组中累加和为给定值的最长子数组长度
【题目】
给定一个数组 arr,该数组无序,但每个值均为正数,再给定一个正数 k。求 arr 的所有子数组中所有元素相加和为 k 的最长子数组长度。
例如,arr=[1,2,1,1,1],k=3。
累加和为 3 的最长子数组为[1,1,1],所以结果返回 3。
【解答】
-
双指针
首先用两个位置来标记子数组的左右两头,记为 left 和 right,开始时都在数组的最左边(left=0,right=0)。整体过程如下:
1.开始时变量 left=0,right=0,代表子数组 arr[left…right]。
2.变量 sum 始终表示子数组 arr[left…right]的和。开始时 sum=arr[0],即 arr[0…0]的和。
3.变量 len 一直记录累加和为 k 的所有子数组中最大子数组的长度。开始时,len=0。
4.根据 sum 与 k 的比较结果决定是 left 移动还是 right 移动,具体如下:
- 如果 sum==k,说明 arr[left…right]累加和为 k,如果 arr[left…right]长度大于 len,则更新len,此时因为数组中所有的值都为正数,那么所有从 left 位置开始,在 right 之后的位置结束的子数组,即 arr[left…i(i>right)],累加和一定大于 k。所以,令 left 加 1,这表示我们开始考查以 left 之后的位置开始的子数组,同时令 sum-=arr[left],sum 此时开始表示 arr[left+1…right]的累加和。
- 如果 sum 小于 k,说明 arr[left…right]还需要加上 right 后面的值,其和才可能达到 k,所以,令 right 加 1,sum+=arr[right]。需要注意的是,right 加 1 后是否越界。
- 如果 sum 大于 k,说明所有从 left 位置开始,在 right 之后的位置结束的子数组,即arr[left…i(i>right)],累加和一定大于 k。所以,令 left 加 1,这表示我们开始考查以 left之后的位置开始的子数组,同时令 sum-=arr[left],sum 此时表示 arr[left+1…right]的累加和。
5.如果 right
【代码】
#include 未排序数组中累加和为给定值的最长子数组系列问题
【题目】
给定一个无序数组 arr,其中元素可正、可负、可 0。给定一个整数 k,求 arr 所有的子数组中累加和为 k 的最长子数组长度。
补充问题 1:给定一个无序数组 arr,其中元素可正、可负、可 0。求 arr 所有的子数组中正数与负数个数相等的最长子数组长度。
补充问题 2:给定一个无序数组 arr,其中元素只是 1 或 0。求 arr 所有的子数组中 0 和 1个数相等的最长子数组长度。
【解答】
-
arr[j…i]= s(i)-s(j-1)
首先来看原问题。为了说明解法,先定义 s 的概念,s(i)代表子数组 arr[0…i]所有元素的累加和。那么子数组arr[j…i](0≤j≤i
原问题解法只遍历一次 arr,具体过程为:
1.设置变量 sum=0,表示从 0 位置开始一直加到 i 位置所有元素的和。设置变量 len=0,表示累加和为 k 的最长子数组长度。设置哈希表 map,其中,key 表示从 arr 最左边开始累加的过程中出现过的 sum 值,对应的 value 值则表示 sum 值最早出现的位置。
2.从左到右开始遍历,遍历的当前元素为 arr[i]。
1)令 sum=sum+arr[i],即之前所有元素的累加和 s(i),在 map 中查看是否存在 sum-k。
-
如果 sum-k 存在,从 map 中取出 sum-k 对应的 value 值,记为 j,j 代表从左到右不断累加的过程中第一次加出 sum-k 这个累加和的位置。根据之前得出的结论,arr[j+1…i]的累加和为 s(i)-s(j),此时 s(i)=sum,又有 s(j)=sum-k,所以 arr[j+1…i]的累加和为 k。同时因为 map 中只记录每一个累加和最早出现的位置,所以此时的 arr[j+1…i]是在必须以arr[i]结尾的所有子数组中,最长的累加和为 k 的子数组,如果该子数组的长度大于 len,就更新 len。
-
如果 sum-k 不存在,说明在必须以 arr[i]结尾的情况下没有累加和为 k 的子数组。
2)检查当前的 sum(即 s(i))是否在 map 中。如果不存在,说明此时的 sum 值是第一次出现的,就把记录(sum,i)加入到 map 中。如果 sum 存在,说明之前已经出现过 sum,map 只记录一个累加和最早出现的位置,所以此时什么记录也不加。
3.继续遍历下一个元素,直到所有的元素遍历完。
大体过程如上,但还有一个很重要的问题需要处理。根据 arr[j+1…i]的累加和为 s(i)-(j),所以,如果从 0 位置开始累加,会导致 j+1≥1。也就是说,所有从 0 位置开始的子数组都没有考虑过。所以,应该从-1 位置开始累加,也就是在遍历之前先把(0,-1)这个记录放进 map,这个记录的意义是如果任何一个数都不加时,累加和为 0。这样,从 0 位置开始的子数组就被我们考虑到了。
-
【代码】
#include 附:
补充问题1:先把数组 arr 中的正数全部变成 1,负数全部变成-1,0 不变,然后求累加和为 0 的最长子数组长度即可。
补充问题2:先把数组 arr 中的 0 全部变成-1,1 不变,然后求累加和为 0 的最长子数组长度即可。
未排序数组中累加和小于或等于给定值的最长子数组长度
【题目】
给定一个无序数组 arr,其中元素可正、可负、可 0。给定一个整数 k,求 arr 所有的子数组中累加和小于或等于 k 的最长子数组长度。
例如:arr=[3,-2,-4,0,6],k=-2,相加和小于或等于-2 的最长子数组为{3,-2,-4,0},所以结果返回 4。
【解答】
-
法一:arr[j…i]= s(i)-s(j-1)
依次求以数组中每个位置结尾的、累加和小于或等于 k 的最长子数组长度,其中最长的那个子数组的长度就是我们要的结果。
如果从 0 位置到 j 位置的累加和为sum[0…j],此时想求以 j 位置结尾的相加和小于或等于 k 的最长子数组长度。那么只要知道大于或等于 sum[0…j]-k 这个值的累加和最早出现在 j 之前的什么位置就可以,假设那个位置是 i 位置,那么 arr[i+1…j]就是在 j 位置结尾的相加和小于或等于 k 的最长子数组。
为了很方便地找到大于或等于某一个值的累加和最早出现的位置,可以按照如下方法生成辅助数组 helpArr。
1.生成 arr 每个位置从左到右的累加和数组 sumArr。以[1,2,-1,5,-2]为例,生成的sumArr=[0,1,3,2,7,5]。注意,sumArr 中的第一个数为 0,表示当没有任何一个数时的累加和为 0。
2.生成 sumArr 的左侧最大值数组 helpArr,sumArr={0,1,3,2,7,5} -> helpArr={0,1,3,3, 7,7}。为什么原来的 sumArr 数组中的 2 和 5 变为 3 和 7 呢?因为我们只关心大于或等于某一个值的累加和最早出现的位置,而累加和 3 出现在 2 之前,并且大于或等于 3,必然大于 2。所以,当然要保留一个更大的、出现更早的累加和。
3.helpArr 是 sumArr 每个位置上左侧的最大值数组,那么它当然是有序的。在这样一个有序的数组中,就可以二分查找大于或等于某一个值的累加和最早出现的位置。例如,在[0,1,3,3,7,7]中查找大于或等于 4 这个值的位置,就是第一个 7 的位置。
【代码】
- 法一
#include -
法二:动态规划+滑动窗口
如果数组 arr 长度为 N,建立两个长度为 N 的数组 minSums[]和 minSumEnds[]。minSums[i]表示必须以 arr[i]开头的所有子数组中,能够得到的最小累加和是多少;minSumEnds[i]表示必须以 arr[i]开头的所有子数组中,如果得到了最小累加和,那么这个最小累加和的子数组右边界在哪个位置。通过动态规划,从右往左遍历一遍就可以生成 minSums[]和 minSumEnds[]这两个数组。以下是一个例子。
位置: 0 1 2 3 4 5
arr = { -3, 9, -6, 4, -2, -1 }
minSums = { -3, 3, -6, 1, -3, -1 }
minSumEnds= { 0, 2, 2, 5, 5, 5 }接下来,从右往左求到任何一个位置 i 时,minSums[i+1]和 minSumEnds[i+1]一定已经求出。必须以 arr[i]开头的子数组可以只包含 arr[i],也可以往右扩,如果往右扩,就一定会包含 arr[i+1]。所以,必须以 arr[i]开头的子数组最小累加和有以下两种可能性:
可能性 1:arr[i],也就是只包含 arr[i]的情况。
可能性 2:arr[i] + minSums[i+1],也就是决定往右扩的情况。
那么,如果 minSums[i+1]<=0 ,那么 minSums[i] = arr[i] + minSums[i+1] , minSumEnds[i] = minSumEnds[i+1],为可能性 2。如果 minSums[i+1]>0,那么 minSums[i] = arr[i],minSumEnds[i] = i,为可能性 1。
接下来用上文举的例子来展示如何利用 minSums[]和 minSumEnds[]这两个数组求解累加和小于或等于 0 的最长子数组。
先看必须以 0 位置开始的所有子数组。因为 minSums[0]为-3,是小于或等于 0 的,又有minSumEnds[0]等于 0(右边界),说明 arr[0…0]是满足累加和小于或等于 0 的。窗口形成了,此时窗口就是arr[0…0],把窗口内的累加和记为 sum,此时 sum 等于-3。那么窗口能继续往右扩吗?窗口右边的下一个位置是 1 位置,minSums[1]为 3,把这个 3 累加进 sum,sum=-3+3=0,是小于或等于 0 的,又有 minSumEnds[1]等于 2(新的右边界),说明 arr[0…2]是满足累加和小于或等于 0 的,窗口扩大了,此时窗口是 arr[0…2],窗口累加和 sum 等于 0。那么窗口还能继续往右扩吗?窗口右边的下一个位置是 3 位置,minSums[3]为 1,如果把这个 1 累加进 sum,就不再满足累加和小于或等于 0 了,所以便知道窗口不能向右边扩了。窗口最终固定在 arr[0…2],长度为 3。
再看必须以 1 位置开始的所有子数组。之前找到的窗口为 arr[0…2],窗口累加和 sum=0,让arr[0]的数出窗口,也就是把窗口缩小成 arr[1…2],sum 当然也要减去 arr[0]的值,就变成了 3。窗口能继续往右扩吗?窗口右边的下一个位置是 3 位置,minSums[3]为 1,如果把这个 1 累加进 sum,不满足累加和小于或等于 0。所以可以知道,窗口不能向右扩。窗口最终固定在了arr[1…2],长度为 2。
这里是整个算法最精髓的地方,大家看一下 arr 数组,必须以 arr[1]开头的所有子数组,根本没有任何一个可以使得累加和小于或等于0。那么此时窗口固定在arr[1…2],这么做有何意义?比如,某一个数组,必须以 34 位置开始的时候,窗口的右边界向右扩到了 100 位置,arr[34…100]这个窗口是必须以 34 位置开始的所有子数组中累加和小于或等于 0 的最长子数组。那么,如果必须以 35 位置开始的所有子数组中,累加和小于或等于 0 的最长子数组是 arr[35…65]。也就是说,必须以 35 位置开始的所有子数组中,客观上确实往右最多只能扩到 65 的位置,也就是扩不到 100 位置更往右的位置。那么其实我们本来也不需要关心从 35 位置开始到底能扩到哪里。因为既然我们已经找到了 arr[34…100],为什么要去关心一个更短的答案呢?也就是说,每次考查必须以 i 位置开始的所有子数组时,扩出来的窗口(假设为 arr[i…j])的含义并不是从 i 位置出发累加和小于或等于 k 的最长子数组。真正的含义是,我们根本就不关心比 arr[i…j]长度更短的答案,只想知道在以 i 位置开始的时候,是否存在把窗口的右边界再往右扩的可能。
再看必须以 2 位置开始的所有子数组。之前找到的窗口为 arr[1…2],窗口累加和 sum=3,让arr[1]的数出窗口,也就是把窗口缩小成 arr[2…2],sum 当然也要减去 arr[1]的值,就变成了-6。窗口能继续往右扩吗?窗口右边的下一个位置是 3 位置,minSums[3]为 1,如果把这个 1 累加进 sum,sum 变成-5,是小于或等于 0 的,又有 minSumEnds[3]等于 5(新的右边界)。说明 arr[2…5]是满足累加和小于或等于 0 的,窗口扩大了,此时窗口是 arr[2…5],窗口累加和 sum 等于-5。那么窗口还能继续往右扩吗?不能,已经来到整个数组的最后一个位置了。arr[2…5]的长度为 4,接下来即便还存在累加和小于或等于 0 的子数组,也不会比 arr[2…5]更长。整个过程中,最大长度为 4,就是答案。
【代码】
- 法二
#include 计算数组的小和
【题目】
数组小和的定义如下: 例如,数组 s=[1,3,5,2,4,6],在 s[0]的左边小于或等于 s[0]的数的和为 0;在 s[1]的左边小于或等于 s[1]的数的和为 1;在 s[2]的左边小于或等于 s[2]的数的和为 1+3=4;在 s[3]的左边小于或等于 s[3]的数的和为 1;在 s[4]的左边小于或等于 s[4]的数的和为 1+3+2=6;在 s[5]的左边小于或等于 s[5]的数的和为 1+3+5+2+4=15。所以 s 的小和为 0+1+4+1+6+15=27。
给定一个数组 s,实现函数返回 s 的小和。
【解答】
-
在归并排序过程中,利用组间在进行合并时产生小和
1.假设左组为 l[],右组为 r[],左右两个组的组内都已经有序,现在要利用外排序合并成 一个大组,并假设当前外排序是 l[i]与 r[j]在进行比较。
2.如果 l[i]<=r[j],那么产生小和。假设从 r[j]往右一直到 r[]结束,元素的个数为 m,那么产生的小和为 l[i]*m。
3.如果 l[i]>r[j],不产生任何小和。
4.整个归并排序的过程该怎么进行就怎么进行,排序过程没有任何变化,只是利用步骤1~步骤 3,也就是在组间合并的过程中累加所有产生的小和,总的累加和就是结果。
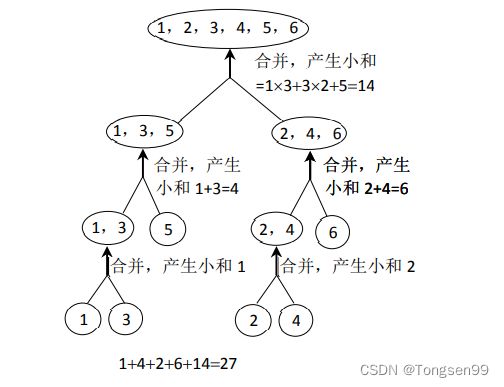
相当于1 * 5 + 3 * 3 + 5 * 1 + 2 * 2 + 4 * 1 = 27(相当于在原数组[1,3,5,2,4,6]从左到右遍历时,1加了5次,3加了3次,5加了1次,2加了2次,4加了1次,6加了0次)。
【代码】
#include 自然数数组的排序
【题目】
给定一个长度为 N 的整型数组 arr,其中有 N 个互不相等的自然数 1~N。请实现 arr 的排序,但是不要把下标 0~N-1 位置上的数通过直接赋值的方式替换成 1~N。
【解答】
-
法一:位置交替成环
arr 在调整之后应该是下标从 0 到 N-1 的位置上依次放着 1~N,即 arr[index]=index+1。
1.从左到右遍历 arr,假设当前遍历到 i 位置。
2.如果 arr[i]=i+1,说明当前的位置不需要调整,继续遍历下一个位置。
3.如果 arr[i]!=i+1,说明此时 i 位置的数 arr[i]不应该放在 i 位置上,接下来将进行跳的过程。
举例说明,比如[1,2,5,3,4],假设遍历到位置 2,也就是 5 这个数。5 应该放在位置 4 上,所以把 5 放进去,数组变成[1,2,5,3,5]。同时,4 这个数是被 5 替下来的数,应该放在位置 3,所以把 4 放进去,数组变成[1,2,5,4,5]。同时,3 这个数是被 4 替下来的数,应该放在位置 2。所以把 3 放进去,数组变成[1,2,3,4,5]。当跳了一圈回到原位置后,会发现此时 arr[i]=i+1,继续遍历下一个位置。
【代码】
- 法一
#include -
法二:在当前位置上与后面其他可能位置交换
1.从左到右遍历 arr,假设当前遍历到 i 位置。
2.如果 arr[i]=i+1,说明当前的位置不需要调整,继续遍历下一个位置。
3.如果 arr[i]!=i+1,说明此时 i 位置的数 arr[i]不应该放在 i 位置上,接下来将在 i 位置进行交换过程。
比如[1,2,5,3,4],假设遍历到位置 2,也就是 5 这个数。5 应该放在位置 4 上,所以位置 4上的数 4 和 5 交换,数组变成[1,2,4,3,5]。但此时还是 arr[2]!=3,4 这个数应该放在位置 3 上,所以 3 和 4 交换,数组变成[1,2,3,4,5]。此时 arr[2]=3,遍历下一个位置。
【代码】
- 法二
#include 奇数下标都是奇数或者偶数下标都是偶数
【题目】
给定一个长度不小于 2 的数组 arr,实现一个函数调整 arr,要么让所有的偶数下标都是偶数,要么让所有的奇数下标都是奇数。
【解答】
-
双指针
1.设置变量 even,表示目前 arr 最左边的偶数下标,初始时 even=0。
2.设置变量 odd,表示目前 arr 最左边的奇数下标,初始时 odd=1。
3.不断检查 arr 的最后一个数,即 arr[N-1]。如果 arr[N-1]是偶数,交换 arr[N-1]和 arr[even],然后令 even=even+2。如果 arr[N-1]是奇数,交换 arr[N-1]和 arr[odd],然后令 odd=odd+2。继续重复步骤 3。
4.如果 even 或者 odd 大于或等于 N,过程停止。
举例说明整个过程。比如[1,8,3,2,4,6],当前最后一个数记为 end=6,even=0,odd=1。此时end=6 为偶数,所以 6 和 arr[even=0]交换,数组变成[6,8,3,2,4,1],even=even+2=2。此时 end=1为奇数,所以 1 和 arr[odd=1]交换,数组变成[6,1,3,2,4,8],odd=odd+2=3。此时 end=8 为偶数,所以 8 和 arr[even=2]交换,数组变成[6,1,8,2,4,3],even=even+2=4。此时 end=3 为奇数,所以 3和 arr[odd=3]交换,数组变成[6,1,8,3,4,2],odd=odd+2=5。此时 end=2 为偶数,所以 2 和 arr[odd=4]交换,数组变成[6,1,8,3,2,4],even=even+2=6。此时 even 大于或等于长度 6,说明偶数下标已经都是偶数,过程停止。
再解释得直白一点,最后位置的数是偶数,就向偶数下标发送,最后位置的数是奇数,就向奇数下标发送,如果偶数下标或者奇数下标已经无法再向右移动,说明调整结束。
【代码】
#include 子数组的最大累加和问题
【题目】
给定一个数组 arr,返回子数组的最大累加和。 例如,arr=[1,-2,3,5,-2,6,-1],所有的子数组中,[3,5,-2,6]可以累加出最大的和 12,所以返回12。
【解答】
-
累加和为正数的小子数组必为最大累加和子数组的左边部分
如果 arr 中没有正数,产生的最大累加和一定是数组中的最大值。
如果 arr 中有正数,从左到右遍历 arr,用变量 cur 记录每一步的累加和,遍历到正数 cur增加,遍历到负数 cur 减少。当 cur<0 时,说明累加到当前数出现了小于 0 的结果,那么累加的这一部分肯定不能作为产生最大累加和的子数组的左边部分,此时令 cur=0,表示重新从下一个数开始累加。当 cur>=0 时,每一次累加都可能是最大的累加和。所以,用另外一个变量 max全程跟踪记录 cur 出现的最大值即可。
举例说明,arr=[1,-2,3,5,-2,6,-1],开始时,max=极小值,cur=0。
遍历到 1,cur=cur+1=1,max 更新成 1。遍历到-2,cur=cur-2=-1,开始出现负的累加和。所以,说明[1,-2]这一部分肯定不会作为产生最大累加和的子数组的左边部分,于是令 cur=0,max不变。遍历到 3,cur=cur+3=3,max 更新成 3。遍历到 5,cur=cur+5=8,max 更新成 8。遍历到-2,cur=cur-2=6,虽然累加了一个负数,但是 cur 依然大于 0,说明累加的这一部分(也就是[3,5,-2])仍可能作为最大累加和的子数组的左边部分。max 不更新。遍历到 6,cur=cur+6=12,max 更新成 12。遍历到-1,cur=cur-1=11,max 不更新。最后返回 12。
解释得再直白一点,cur 累加成为负数就清零重新累加,max 记录 cur 的最大值即可。
【代码】
#include 子矩阵的最大累加和问题
【题目】
给定一个矩阵 matrix,其中的值有正、有负、有 0,返回子矩阵的最大累加和。
例如,矩阵 matrix 为:
-90 48 78
64 -40 64
-81 -7 66
其中,最大累加和的子矩阵为:
48 78
-40 64
-7 66
所以返回累加和 209。
例如,matrix 为:
-1 -1 -1
-1 2 2
-1 -1 -1
其中,最大累加和的子矩阵为:
2 2
所以返回累加和 4。
【解答】
-
借助子数组的最大累加和,在累加和数组的基础上求最大累加和
首先来看这样一个例子,假设一个 2 行 4 列的矩阵如下:
-2 3 -5 7
1 4 -1 -3
如何求必须含有 2 行元素的子矩阵中的最大累加和?可以把两列的元素累加,然后得到累加数组[-1,7,-6,4],接下来求这个累加数组的最大累加和,结果是 7。也就是说,必须含有 2 行元素的子矩阵中的最大和为 7,且这个子矩阵是:
3
4
也就是说,如果一个矩阵一共有 k 行且限定必须含有 k 行元素的情况下,我们只要把矩阵中每一列的 k 个元素累加生成一个累加数组,然后求出这个数组的最大累加和,这个最大累加和就是必须含有 k 行元素的子矩阵中的最大累加和。
对于矩阵 matrix 为:
-90 48 78
64 -40 64
-81 -7 66
首先考虑只有一行的矩阵[-90,48,78],因为只有一行,所以累加数组 arr就是[-90,48,78],这个数组的最大累加和为 126。
接下来考虑含有两行的矩阵:
-90 48 78
64 -40 64
这个矩阵的累加数组就是在上一步的累加数组[-90,48,78]的基础上,依次在每个位置上加上矩阵最新一行[64, -40, 64]的结果,即[-26,8,142],这个数组的最大累加和为 150。
接下来考虑含有三行的矩阵:
-90 48 78
64 -40 64
-81 -7 66
这个矩阵的累加数组就是在上一步累加数组[-26,8,142]的基础上,依次在每个位置上加上矩阵最新一行[-81,-7,66]的结果,即[-107,1,208],这个数组的最大累加和为 209。
此时,必须从矩阵的第一行元素开始,并往下的所有子矩阵已经查找完毕,接下来从矩阵的第二行开始,继续这样的过程,含有一行矩阵:
64 -40 64
因为只有一行,所以累加数组就是[64,-40,64],这个数组的最大累加和为 88。
接下来考虑含有两行的矩阵:
64 -40 64
-81 -7 66
这个矩阵的累加数组就是在上一步累加数组[64,-40,64]的基础上,依次在每个位置上加上矩阵最新一行[-81,-7,66]的结果,即[-17,-47,130],这个数组的最大累加和为 130。
此时,必须从矩阵的第二行元素开始,并往下的所有子矩阵已经查找完毕,接下来从矩阵的第三行开始,继续这样的过程,含有一行矩阵:
-81 -7 66
因为只有一行,所以累加数组就是[-81,-7,66],这个数组的最大累加和为 66。
全部过程结束,所有的子矩阵都已经考虑到了,结果为以上所有最大累加和中最大的 209。
整个过程最关键的地方有两处:
- 用求累加数组的最大累加和的方式得到每一步的最大子矩阵的累加和。
- 每一步的累加数组可以利用前一步求出的累加数组很方便地更新得到。
【代码】
#include 在数组中找到一个局部最小的位置
【题目】
定义局部最小的概念。arr 长度为 1 时,arr[0]是局部最小。arr 的长度为 N(N>1)时,如果 arr[0]
【解答】
-
二分查找
1.如果 arr 为空或者长度为 0,返回-1 表示不存在局部最小。
2.如果 arr 长度为 1 或者 arr[0]
3.如果 arr[N-1]
4.如果 arr 长度大于 2 且 arr 的左右两头都不是局部最小,则令 left=1,right=N-2,然后进入步骤 5 做二分查找。
5.令 mid=(left+right)/2,然后进行如下判断:
1)如果 arr[mid]>arr[mid-1],可知在 arr[left…mid-1]上肯定存在局部最小,令 right=mid-1,重复步骤 5。
2)如果不满足 1),但 arr[mid]>arr[mid+1],可知在 arr[mid+1…right]上肯定存在局部最小,令 left=mid+1,重复步骤 5。
3)如果既不满足 1),也不满足 2),那么 arr[mid]就是局部最小,直接返回 mid。
6.步骤 5 一直进行二分查找,直到 left==right 时停止,返回 left 即可。
如此可见,二分查找并不是数组有序时才能使用,只要你能确定二分两侧的某一侧肯定存在你要找的内容,就可以使用二分查找。
【代码】
#include 数组中子数组的最大累乘积
【题目】
给定一个 double 类型的数组 arr,其中的元素可正、可负、可 0,返回子数组累乘的最大乘积。例如,arr=[-2.5,4,0,3,0.5,8,-1],子数组[3,0.5,8]累乘可以获得最大的乘积 12,所以返回 12。
【解答】
-
比较上个元素的最大累乘积和最小累乘积与当前元素的乘积选出当前的最大累乘积,同时顺便选出当前的最小累乘积
所有的子数组都会以某一个位置结束,所以,如果求出以每一个位置结尾的子数组最大的累乘积,在这么多最大累乘积中最大的那个就是最终的结果。也就是说,结果=max{以 arr[0]结尾的所有子数组的最大累乘积,以arr[1]结尾的所有子数组的最大累乘积……以 arr[arr.size()-1]结尾的所有子数组的最大累乘积}。
如何快速求出所有以 i 位置结尾(arr[i])的子数组的最大乘积呢?假设以 arr[i-1]结尾的最小累乘积为 min,以 arr[i-1]结尾的最大累乘积为 max。那么,以 arr[i]结尾的最大累乘积只有以下三种可能:
- 可能是 max * arr[i]。max 既然表示以 arr[i-1]结尾的最大累乘积,那么当然有可能以 arr[i]结尾的最大累乘积是 max * arr[i]。例如,[3,4,5]在算到 5 的时候。
- 可能是 min * arr[i]。min 既然表示以 arr[i-1]结尾的最小累乘积,当然有可能 min 是负数,而如果 arr[i]也是负数,两个负数相乘的结果也可能很大。例如,[-2,3,-4]在算到-4的时候。
- 可能仅是 arr[i]的值。以 arr[i]结尾的最大累乘积并不一定非要包含 arr[i]之前的数。例如,[0.1,0.1,100]在算到 100 的时候。
这三种可能的值中最大的那个就作为以 i 位置结尾的最大累乘积,最小的作为最小累乘积,然后继续计算以 i+1 位置结尾的时候,如此重复,直到计算结束。
【代码】
#include 打印 N 个数组整体最大的 Top K
【题目】
有 N 个长度不一的数组,所有的数组都是有序的,请从大到小打印这 N 个数组整体最大的前 K 个数。
例如,输入含有 N 行元素的二维数组可以代表 N 个一维数组。
219,405,538,845,971
148,558
52,99,348,691
再输入整数 k=5,则打印:
Top 5: 971,845,691,558,538
【解答】
-
利用堆结构和堆排序
1.构建一个大小为 N 的大根堆 heap,建堆的过程就是把每个数组中的最后一个值(也就是该数组的最大值)依次加入堆里,这个过程是建堆时的调整过程(heapInsert)。
2.建好堆之后,此时 heap 堆顶的元素是所有数组的最大值中最大的那个,打印堆顶元素。
3.假设堆顶元素来自 a 数组的 i 位置。那么接下来就把堆顶的前一个数(即 a[i-1])放在heap 的头部,也就是用 a[i-1]替换原本的堆顶,然后从堆的头部开始调整堆,使其重新变为大根堆(heapify 过程)。
4.这样每次都可以得到一个堆顶元素 max,在打印完成后都经历步骤 3 的调整过程。整体打印 k 次,就是从大到小全部的 Top K。
5.在重复步骤 3 的过程中,如果 max 来自的那个数组(仍假设是 a 数组)已经没有元素。也就是说,max 已经是 a[0],再往左没有数了。那么就把 heap 中最后一个元素放在 heap 头部的位置,然后把 heap 的大小减 1(heapSize-1),最后依然是从堆的头部开始调整堆,使其重新变为大根堆(堆大小减 1 之后的 heapify 过程)。
6.直到打印了 k 个数,过程结束。
【代码】
#include heap时没有进行有参构造
HeapNode() {}
HeapNode(int value, int arrNum, int index)
{
this->value = value;
this->arrNum = arrNum;
this->index = index;
}
~HeapNode() {}
};
class getNumber
{
public:
void printTopK(vector<vector<int>> matrix, int topK)
{
int heapSize = matrix.size();
vector<HeapNode> heap(heapSize);
for (int i = 0; i < heapSize; i++)
{
int index = matrix[i].size() - 1;
HeapNode node(matrix[i][index], i, index);
heapInsert(heap, i, node);
}
cout << "Top" << topK << ":";
for (int i = 0; i < topK; i++)
{
if (heapSize == 0)
{
break;
}
cout << heap[0].value << " ";
if (heap[0].index != 0)
{
heap[0].value = matrix[heap[0].arrNum][--heap[0].index];
}
else
{
swap(heap, 0, --heapSize);
}
heapify(heap, 0, heapSize);
}
}
//建堆
void heapInsert(vector<HeapNode> &heap, int index, HeapNode node)
{
heap[index] = node;
while (index != 0)
{
int parent = (index - 1) / 2;
if (heap[parent].value < heap[index].value)
{
swap(heap, parent, index);
index = parent;
}
else
{
break;
}
}
}
//调整堆
void heapify(vector<HeapNode> &heap, int index, int heapSize)
{
int left = index * 2 + 1, right = index * 2 + 2, largest = index;
while (left < heapSize)
{
if (heap[left].value > heap[index].value)
{
largest = left;
}
if (right < heapSize && heap[right].value > heap[largest].value)
{
largest = right;
}
if (largest != index)
{
swap(heap, index, largest);
}
else
{
break;
}
index = largest;
left = index * 2 + 1;
right = index * 2 + 2;
}
}
void swap(vector<HeapNode> &heap, int index1, int index2)
{
HeapNode temp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = temp;
}
};
int main()
{
int N, K, t;
string s;
scanf("%d%d", &N, &K);
getchar();
vector<vector<int>> matrix(N);
for (int i = 0; i < N; i++)
{
getline(cin, s);
stringstream ssin(s); //使用字符串流stringstream,读取单个数字或字符。
while (ssin >> t)
{
matrix[i].push_back(t);
}
}
getNumber *p = new getNumber();
p->printTopK(matrix, K);
system("pause");
return 0;
}
边界都是 1 的最大正方形大小
【题目】
给定一个 N×M 的矩阵 matrix,在这个矩阵中,只有 0 和 1 两种值,返回边框全是 1 的最大正方形的边长长度。
例如:
0 1 1 1 1
0 1 0 0 1
0 1 0 0 1
0 1 1 1 1
0 1 0 1 1
其中,边框全是 1 的最大正方形的大小为 4×4,所以返回 4。
【解答】
-
矩阵预处理
1.矩阵中一共有 N×M 个位置。
2.对每一个位置都看是否可以成为边长为 size~1 的正方形左上角。比如,对于(0,0)位置,依次检查是否是边长为 5 的正方形左上角,然后检查边长为 4、3 等。
3.如何检查一个位置是否可以成为边长为 size 的正方形的左上角呢?可以遍历这个边长为 size 的正方形边界看是否只由 1 构成,也就是走过 4 个边的长度。以下为对这一步骤的优化过程。
检查一个位置假设为(i,j),是否可以作为边长为 a(1≤a≤min(N,M))的边界全是 1 的正方形左上角。关键是使用预处理技巧。下面介绍得到预处理矩阵的过程。
1.预处理过程是根据矩阵 matrix 得到两个矩阵 right 和 down。right[i] [j]的值表示从位置(i,j)出发向右,有多少个连续的 1。down[i] [j]的值表示从位置(i,j)出发向下有多少个连续的 1。
2.right 和 down 矩阵如何计算?
1)从矩阵的右下角(n-1,n-1)位置开始计算,如果 matrix[n-1] [n-1]=1,那么,right[n-1] [n-1]=1且 down[n-1] [n-1]=1,否则都等于 0。
2)从右下角开始往上计算,即在 matrix 最后一列上计算,位置就表示为(i,n-1)。对 right矩阵来说,最后一列的右边没有内容。所以,如果 matrix[i] [n-1]=1,则令 right[i] [n-1]=1,否则为 0。对 down 矩阵来说,如果 matrix[i] [n-1]=1,因为 down[i+1] [n-1]表示包括位置(i+1,n-1)在内并往下有多少个连续的 1。所以,如果位置(i,n-1)是 1,那么,令 down[i] [n-1]=down[i+1] [n-1]+1;如果 matrix[i] [n-1]=0,则令 down[i] [n-1]=0。
3)从右下角开始往左计算,即在 matrix 最后一行上计算,位置可以表示为(n-1,j)。对 right矩阵来说,如果 matrix[n-1] [j]=1,因为 right[n-1] [j+1]表示包括位置(n-1,j+1)在内右边有多少个连续的 1。所以,如果位置(n-1,j)是 1,则令 right[n-1] [j]=right[n-1] [j+1]+1;如果matrix[n-1] [j]=0,则令 right[n-1] [j]=0。对 down 矩阵来说,最后一列的下边没有内容。所以,如果 matrix[n-1] [j]=1,令 down[n-1] [j]=1,否则为 0。
4)计算完步骤 1)~步骤 3)之后,剩下的位置都是既有右,也有下,假设位置表示为(i,j):
- 如果 matrix[i] [j]=1,则令 right[i] [j]=right[i] [j+1]+1,down[i] [j]=down[i+1] [j]+1。
- 如果 matrix[i] [j]=0,则令 right[i] [j]=0,down[i] [j]=0。
得到 right 和 down 矩阵后,如何加速检查过程呢?比如现在想检查一个位置,假设为(i,j)。是否可以作为边长为 a(1≤a≤N)的边界全为 1 的正方形左上角。
1)位置(i,j)的右边和下边连续为 1 的数量必须都大于或等于 a(right[i][j]>=a&&down[i] [j]>=a),否则说明上边界和左边界的 1 不够。
2)位置(i,j)向右跳到位置(i,j+a-1),这个位置是正方形的右上角,那么这个位置的下边连续为 1 的数量也必须大于或等于 a(down[i] [j+a-1]>=a),否则说明右边界的 1 不够。
3)位置(i,j)向下跳到位置(i+a-1,j),这个位置是正方形的左下角,那么这个位置的右边连续为 1 的数量也必须大于或等于 a(right[i+a-1] [j]>=a),否则说明下边界的 1 不够。
以上三个条件都满足时,就说明位置(i,j)符合要求,利用 right 和 down 矩阵之后,加速的过程很明显,就不需要遍历边长上的所有值了,只看 4 个点即可。
【代码】
#include 不包含本位置值的累乘数组
【题目】
给定一个整型数组 arr,返回不包含本位置值的累乘数组。
例如,arr=[2,3,1,4],返回[12,8,24,6],即除自己外,其他位置上的累乘。
【解答】
-
法一:逆向思维即使用除法实现
结果数组记为 res,所有数的乘积记为 all。如果数组中不含 0, 则设置 res[i]=all/arr[i](0≤i≤n)即可。如果数组中有 1 个 0,对唯一的 arr[i]==0 的位置令 res[i]=all, 其他位置上的值都是 0 即可。如果数组中 0 的数量大于 1,那么 res 所有位置上的值都是 0。
【代码】
- 法一
#include -
法二:数组预处理并且复用数组
1.生成两个长度和 arr 一样的新数组 lr[]和 rl[]。lr[]表示从左到右的累乘(即 lr[i]=arr[0…i])的累乘。rl 表示从右到左的累乘(即 rl[i]=arr[i…N-1])的累乘。
2.一个位置上除去自己值的累乘,就是自己左边的累乘再乘以自己右边的累乘,即res[i]=lr[i-1]*rl[i+1]。
3.最左位置和最右位置的累乘比较特殊,即 res[0]=rl[1],res[N-1]=lr[N-2]。
以上思路虽然可以得到结果 res,但是除 res 之外,又使用了两个额外数组,怎么省掉这两个额外数组呢?可以通过 res 数组复用的方式。也就是说,先把 res 数组作为辅助计算的数组,然后把 res 调整成结果数组返回。
【代码】
- 法二
#include 数组的 partition 调整
【题目】
给定一个有序数组 arr,调整 arr 使得这个数组的左半部分没有重复元素且升序,而不用保证右部分是否有序。
例如,arr=[1,2,2,2,3,3,4,5,6,6,7,7,8,8,8,9],调整之后 arr=[1,2,3,4,5,6,7,8,9,…]。
【解答】
-
双指针
1.生成变量 u,含义是在 arr[0…u]上都是无重复元素且升序的。也就是说,u 是这个区域最后的位置,初始时 u=0,这个区域记为 A。
2.生成变量 i,利用 i 做从左到右的遍历,在 arr[u+1…i]上是不保证没有重复元素且升序的区域,i 是这个区域最后的位置,初始时 i=1,这个区域记为 B。
3.i 向右移动(i++)。因为数组整体有序,所以,如果 arr[i]!=arr[u],说明当前数 arr[i]应该加入到 A 区域里,交换 arr[u+1]和 arr[i],此时 A 的区域增加一个数(u++);如果 arr[i]=arr[u],说明当前数 arr[i]的值之前已经加入 A 区域,此时不用再加入。
4.重复步骤 3,直到所有的数遍历完。
【代码】
#include 补充问题:给定一个数组 arr,其中只可能含有 0、1、2 三个值,请实现 arr 的排序。
另一种问法为:有一个数组,其中只有红球、蓝球和黄球,请实现红球全放在数组的左边,蓝球放在中间,黄球放在右边。
另一种问法为:有一个数组,再给定一个值 k,请实现比 k 小的数都放在数组的左边,等于 k 的数都放在数组的中间,比 k 大的数都放在数组的右边。
【解答】
-
三指针( [left…index…right] 根据指针划分左中右三区)
1.生成变量 left,含义是在 arr[0…left](左区)上都是 0,left 是这个区域当前最右的位置,初始时 left 为-1。
2.生成变量 index,利用这个变量做从左到右的遍历,含义是在 arr[left+1…index](中区)上都是 1,index 是这个区域当前最右的位置,初始时 index 为 0。
3.生成变量 right,含义是在 arr[right…N-1](右区)上都是 2,right 是这个区域当前最左的位置,初始时 right 为 N。
4.index 表示遍历到 arr 的一个位置:
1)如果 arr[index]=1,这个值应该直接加入到中区,index++之后重复步骤 4。
2)如果 arr[index]=0,这个值应该加入到左区,arr[left+1]是中区最左的位置,所以把arr[index]和 arr[left+1]交换之后,左区就扩大了,index++之后重复步骤 4。
3)如果 arr[index]=2,这个值应该加入到右区,arr[right-1]是右区最左边数的左边,但也不属于中区,总之,在中区和右区的中间部分。把 arr[index]和 arr[right-1]交换之后,右区就向左扩大了(right–),但是此时 arr[index]上的值未知,所以 index 不变,重复步骤 4。
5.当 index=right 时,说明中区和右区成功对接,三个区域都划分好后,过程停止。 在遍历中的每一步,要么 index 增加,要么 right 减少。如果 index=right,过程就停止。
【代码】
#include 求最短通路值
【题目】
用一个整型矩阵 matrix 表示一个网络,1 代表有路,0 代表无路,每一个位置只要不越界,都有上下左右 4 个方向,求从最左上角到最右下角的最短通路值。
例如,matrix 为:
1 0 1 1 1
1 0 1 0 1
1 1 1 0 1
0 0 0 0 1
通路只有一条,由 12 个 1 构成,所以返回 12。
【解答】
-
宽度优先遍历
设矩阵大小为 N×M,具体过程如下:
1.开始时生成 map 矩阵,map[i] [j]的含义是从(0,0)位置走到(i,j)位置最短的路径值。然后将左上角位置(0,0)的行坐标与列坐标放入行队列 rQ 和列队列 cQ。
2.不断从队列弹出一个位置(r,c),然后看这个位置的上下左右四个位置哪些在 matrix 上的值是 1,这些都是能走的位置。
3.将那些能走的位置设置好各自在 map 中的值,即 map[r] [c]+1。同时将这些位置加入 rQ和 cQ 中,用队列完成宽度优先遍历。
4.在步骤 3 中,如果一个位置之前走过,就不要重复走,这个逻辑可以根据一个位置在 map 中的值来确定,比如 map[i] [j]!=0,就可以知道这个位置之前已经走过。
5.一直重复步骤 2~步骤 4。直到遇到右下角位置,说明已经找到终点,返回终点在 map中的值即可,如果 rQ 和 cQ 已经为空都没有遇到终点位置,说明不存在这样一条路径,返回 0。
【代码】
#include - 把rQ和cQ两个queue合并成一个
#include 数组中未出现的最小正整数
【题目】
给定一个无序整型数组 arr,找到数组中未出现的最小正整数。
例如:
arr=[-1,2,3,4]。返回 1。
arr=[1,2,3,4]。返回 5。
【解答】
-
双指针
设 arr 长度为 N,具体过程如下:
1.在遍历 arr 之前先生成两个变量。变量 l 表示遍历到目前为止,数组 arr 已经包含的正整数范围是[1,l],所以没有开始遍历之前令 l=0,表示 arr 目前没有包含任何正整数。变量 r 表示遍历到目前为止,在后续出现最优状况的情况下,arr 可能包含的正整数范围是[1,r],所以没有开始遍历之前,令 r=N,因为还没有开始遍历,所以后续出现的最优状况是 arr 包含 1~N 所有的整数。r 同时表示 arr 当前的结束位置。
2.从左到右遍历 arr,遍历到位置 l,位置 l 的数为 arr[l]。
3.如果 arr[l]=l+1。没有遍历 arr[l]之前,arr 已经包含的正整数范围是[1,l],此时出现了arr[l]=l+1 的情况,所以 arr 包含的正整数范围可以扩到[1,l+1],即令 l++。然后重复步骤 2。
4.如果arr[l]<=l。没有遍历arr[l]之前,arr在后续最优的情况下可能包含的正整数范围是[1,r],已经包含的正整数范围是[1,l],所以需要[l+1,r]上的数。而此时出现了 arr[l]<=l,说明[l+1,r]范围上的数少了一个,所以 arr 在后续最优的情况下,可能包含的正整数范围缩小了,变为[1,r-1],此时把 arr 最后位置的数(arr[r-1])放在位置 l 上,下一步检查这个数,然后令 r–(相当于去掉位置 l 上的数,位置 l 的后面部分整体前移一个单位)。重复步骤 2。
5.如果 arr[l]>r,与步骤 4 同理,把 arr 最后位置的数(arr[r-1])放在位置 l 上,下一步检查这个数,然后令 r–。重复步骤 2。
6.如果 arr[arr[l]-1]=arr[l]。如果步骤 4 和步骤 5 没中,同时步骤 3 也没中,说明 arr[l](此时 l+2<=arr[l]<=r)是在[l+1,r]范围上的数,而且这个数应该放在 arr[l]-1(arr[l]-1>=l+1,说明位置 arr[l]-1在包括位置 l+1 的后半部分上) 位置上。可是此时发现 arr[l]-1 位置上的数已经是 arr[l],说明出现了两个 arr[l],既然在[l+1,r]上出现了重复值,那么[l+1,r]范围上的数又少了一个,所以与步骤 4和步骤 5 一样,把 arr 最后位置的数(arr[r-1])放在位置 l 上,下一步检查这个数,然后令 r–。重复步骤 2。
7.如果步骤 4、步骤 5 和步骤 6 都没中,说明发现了[l+1,r]范围上的数,并且此时并未发现重复。那么 arr[l]应该放到 arr[l]-1 位置上,所以把 l 位置上的数和 arr[l]-1 位置上的数交换(把数放到应该在的位置上),下一步继续遍历 l 位置上的数。重复步骤 2。
8.最终 l 位置和 r 位置会碰在一起(l=r),arr 已经包含的正整数范围是[1,l],返回 l+1 即可。
【代码】
#include 数组排序之后相邻数的最大差值
【题目】
给定一个整型数组 arr,返回排序后相邻两数的最大差值。
例如:
arr=[9,3,1,10]。如果排序,结果为[1,3,9,10],9 和 3 的差为最大差值,故返回 6。
arr=[5,5,5,5]。返回 0。
【解答】
-
桶排序
遍历 arr 找到最小值和最大值,分别记为 min 和 max。如果 arr 的长度为 N,那么我们准备 N+1 个桶,把 max 单独放在第 N+1 号桶里。arr 中在[min,max)范围上的数放在 1~N 号桶里,对于 1~N 号桶中的每一个桶来说,负责的区间大小为(max-min)/N。比如长度为 10 的数组 arr 中,最小值为 10,最大值为 110。那么就准备 11 个桶,arr 中等于 10 的数全部放在第 1 号桶里,等于 110 的数全部放在第 11 号桶里(则除去最大值的 N-1 个数分给 N 个桶)。区间[10,20)的数全部放在 1 号桶里,区间[20,30)的数全部放在 2 号桶里……,区间[100,110)的数全部放在 10 号桶里。那么如果一个数为 num,它应该分配进(num - min) × len / (max - min)号桶里。
arr 一共有 N 个数,min 一定会放进 1 号桶里,max 一定会放进最后的桶里。所以,如果把所有的数放入 N+1 个桶中,必然有桶是空的。如果 arr 经过排序,相邻的数有可能此时在同一个桶中,也可能在不同的桶中。在同一个桶中的任何两个数的差值都不会大于区间值,而在空桶左右两边不空的桶里,相邻数的差值肯定大于区间值。所以产生最大差值的两个相邻数肯定来自不同的桶。所以只要计算桶之间数的间距就可以,也就是只用记录每个桶的最大值和最小值,最大差值只可能来自某个非空桶的最小值减去前一个非空桶的最大值(保证相邻)。
【代码】
#include 做项目的最大收益问题
【题目】
给定两个整数 W 和 K,W 代表你拥有的初始资金,K 代表你最多可以做 K 个项目。再给定两个长度为 N 的正数数组 costs[]和 profits[],代表一共有 N 个项目,costs[i]和 profits[i]分别表示第 i 号项目的启动资金与做完后的利润(注意是利润,如果一个项目启动资金为 10,利润为 4,代表该项目最终的收入为 14)。你不能并行只能串行地做项目,并且手里拥有的资金大于或等于某个项目的启动资金时,你才能做这个项目。该如何选择做项目,能让你最终的收益最大?返回最后能获得的最大资金。
例如:
W = 3
K = 2
costs = {5, 4, 1, 2}
profits = {3, 5, 3, 2}
初始资金为 3,最多做 2 个项目,每个项目的启动资金与利润见 costs 和 profits。最优选择为:先做 2 号项目,做完之后资金增长到 6。然后做 1 号项目,做完之后资金增长到 11。其他的任何选择都不会比这种选择好,所以返回 11。
【解答】
-
小根堆+大根堆
1.定义项目类,包括项目的花费和项目的利润。
2.生成小根堆 costMinHeap,可以把具体的 Program 放进 costMinHeap 中,根据 Program 的花费来组织小根堆,花费最少的 Program 放在 costMinHeap 的堆顶。
3.生成大根堆 profitMaxHeap,可以把具体的 Program 放进 profitMaxHeap 中,根据 Program 的利润来组织大根堆,利润最多的 Program 放在 profitMaxHeap 的堆顶。
4.根据 costs 和 profits 数组,可以得到所有的 Program,把所有的 Program 放进 costMinHeap。
5.根据当前的资金 W,来解锁 costMinHeap 中的项目,只要是花费小于或等于 W 的项目,就从 costMinHeap 中弹出,放入 profitMaxHeap。因为 costMinHeap 是小根堆,所以依次弹出 Program,直到 costMinHeap 为空或者剩下项目的花费都大于 W,弹出过程停止。每一个从 costMinHeap 弹出的 Program,都进入 profitMaxHeap。进入步骤 6。
6.profitMaxHeap 装着所有可以被考虑和被解锁的项目。
1)如果经历了步骤 5 的解锁过程之后,发现 profitMaxHeap 为空,首先说明当前资金 W 并没有解锁出任何项目,其次说明目前已经没有任何项目可以挑选了。直接返回 W。
2)如果经历了步骤 5 的解锁过程之后,发现 profitMaxHeap 不为空。选择位于 profitMaxHeap 堆顶的那个项目完成,记为 ProgramBest。因为在所有可以被考虑的项目中,profitMaxHeap 堆顶的项目一定是获得利润最多的项目。完成 ProgramBest 之后,可以获得 ProgramBest 的利润,所以 W+=ProgramBest.profit。然后重复步骤 5,进行新一轮的解锁。
7.如果步骤 6 进行的过程中没有返回。那么做完 K 个项目后,返回 W。
【代码】
#include 分金条的最小花费
【题目】
给定一个正数数组 arr,arr 的累加和代表金条的总长度,arr 的每个数代表金条要分成的长度。规定长度为 K 的金条只需分成两块,费用为 K 个铜板。返回把金条分出 arr 中的每个数字需要的最小代价。
例如,arr={10,30,20},金条总长度为 60。 如果先分成 40 和 20 两块,将花费 60 个铜板,再把长度为 40 的金条分成 10 和 30 两块,将花费 40 个铜板,总花费为 100 个铜板;如果先分成 10 和 50 两块,将花费 60 个铜板,再把长度为 50 的金条分成 20 和 30 两块,将花费 50 个铜板,总花费为 110 个铜板;如果先分成 30 和 30 两块,将花费 60 个铜板,再把其中一根长度为 30 的金条分成 10 和 20 两块,将花费 30 个铜板,总花费为 90 个铜板。所以返回最低花费为 90。
【解答】
-
贪心策略(哈夫曼编码算法)
0.假设最小代价为 ans,初始时 ans=0。先把 arr 中所有的数字放进一个小根堆。
1.从小根堆中弹出两个数字,假设为 a 和 b,令 ans=ans+a+b,然后把 a+b 的和放进小根堆。
2.重复步骤 1,直到小根堆中只剩一个数字过程停止,返回 ans 即可。
举个例子,假设 arr={3,9,5,2,4,4},准备变量 ans 和小根堆 minHeap。
0.初始时 ans=0,把 arr 中所有的数字放进 minHeap,minHeap 含有数字{3,9,5,2,4,4},并按照小根堆组织。
1.minHeap 是小根堆,所以弹出 2 和 3,令 ans=0+5=5,然后把 5 放进 minHeap,minHeap 含有数字{5,9,5,4,4},并按照小根堆组织。
2.minHeap 是小根堆,所以弹出 4 和 4,令 ans=5+8=13,然后把 8 放进 minHeap,minHeap 含有数字{8,5,9,5},并按照小根堆组织。
3.minHeap 是小根堆,所以弹出 5 和 5,令 ans=13+10=23,然后把 10 放进 minHeap,minHeap 含有数字{10,8,9},并按照小根堆组织。
4.minHeap 是小根堆,所以弹出 8 和 9,令 ans=23+17=40,然后 17 放进 minHeap,minHeap 含有数字{17,10},并按照小根堆组织。
5.minHeap 是小根堆,所以弹出 17 和 10,令 ans=40+27=67,然后 27 放进 minHeap,minHeap 含有数字{27},并按照小根堆组织。
6.此时小根堆只剩一个数字了,返回 ans=67。
上述过程相当于构建了一棵树。这棵树的所有非叶节点值加起来,就是 ans 的最后结果。同时这棵树从上往下看也知道了如果去分割,先把 27 的金条分成 10 和 17,10 分成 5 和 5,17 分成 8 和 9,其中的一个 5 分成 2 和 3,8 分成 4 和 4。
【代码】
#include 大楼轮廓问题
【题目】
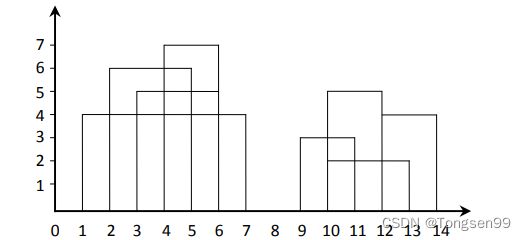
给定一个 N×3 的矩阵 matrix,对于每一个长度为 3 的小数组 arr,都表示一个大楼的三个数据。arr[0]表示大楼的左边界,arr[1]表示大楼的右边界,arr[2]表示大楼的高度(一定大于 0)。每座大楼的地基都在 X 轴上,大楼之间可能会有重叠,请返回整体的轮廓线数组。
例如,matrix =
{
{2,5,6}, {1,7,4}, {4,6,7}, {3,6,5}, {10,13,2}, {9,11,3}, {12,14,4}, {10,12,5}
}
代表的图像如图所示。
返回的轮廓线数组如下:
{
{1,2,4}, {2,4,6}, {4,6,7}, {6,7,4}, {9,10,3}, {10,12,5}, {12,14,4}
}
【解答】
-
有序表结构(sortedMap 或叫 orderedMap)
有序表结构是把所有在其中的数据按照 key 的排序来组织,并提供如下操作。
1)将一个(key,value)记录加入到表中,或者将 key 的记录更新成 value。
2)根据给定的 key,查询 value 并返回。
3)移除 key 的记录。
4)询问是否有关于 key 的记录。
5)返回所有键值的排序结果中,最左(最小)的那个。
6)返回所有键值的排序结果中,最右(最大)的那个。
7)如果表中存入过 key,返回 key;否则返回所有键值的排序结果中,key 的前一个。
8)如果表中存入过 key,返回 key;否则返回所有键值的排序结果中, key 的后一个。
每一个大楼数组都可以看作在左边界新加了一个高度,在右边界删掉了一个高度,比如 {1,7,4}这个大楼,可以看作在 1 这个点新加了一个高度 4,在 7 这个点删除了一个高度 4。所以一个大楼数组可以生成两个描述高度变化的对象。比如{1,7,4}这个大楼数组可以生成{1,加入,一个高度 4}和{7,删除,一个高度 4}这两个描述高度变化的对象。
第一步:将所有的大楼数组变成描述高度变化的对象。
比如题目中的例子,matrix = { {2,5,6}, {1,7,4}, {4,6,7}, {3,6,5}, {10,13,2}, {9,11,3}, {12,14,4}, {10,12,5} } 会变成描述高度变化的对象数组如下:
{
{2,加入,一个高度 6},{5,删除,一个高度 6}, {1,加入,一个高度 4},{7,删除,一个高度 4},{4,加入,一个高度 7},{6,删除,一个高度 7}, {3,加入,一个高度 5},{6,删除,一个高度 5},{10,加入,一个高度 2},{13,删除,一个高度 2}, {9,加入,一个高度 3},{11,删除,一个高度 3}, {12,加入,一个高度 4},{14,删除,一个高度 4}, {10,加入,一个高度 5},{12,删除,一个高度 5}
}
第二步:将描述高度变化的对象数组排序,排序的比较策略如下。
1.第一个维度的值从小到大排序。
2.如果第一个维度的值相等,看第二个维度的值,“加入”排在前,“删除”排在后。
3.如果两个对象第一维度和第二个维度的值都相等,则认为两个对象相等,谁在前都行。
比如上一步的对象数组,排序之后的结果为:
{
{1,加入,一个高度 4}, {2,加入,一个高度 6}, {3,加入,一个高度 5},{4,加入,一个高度 7}, {5,删除,一个高度 6}, {6,删除,一个高度 5}, {6,删除,一个高度 7}, {7,删除,一个高度 4}, {9,加入,一个高度 3}, {10,加入,一个高度 5}, {10,加入,一个高度 2}, {11,删除,一个高度 3}, {12,加入,一个高度 4}, {12,删除,一个高度 5}, {13,删除,一个高度 2}, {14,删除,一个高度 4}
}
第三步:按如下操作。
1)准备有序表 mapHeightTimes,key 是一个整数,代表高度,value 是这个高度目前出现的次数。当某个 key 出现的次数为 0,则删掉这条记录。一开始 mapHeight 中没有任何记录。
2)准备有序表 mapXvalueHeight,key 是一个整数,代表 X 轴上的一个位置,value 是这个位置上的最大高度。当某个 key 出现的次数为 0 时,删掉这条记录。一开始 mapXvalueHeight中没有任何记录。
第四步:根据第二步生成的描述高度变化的数组,对 mapHeightTimes 和 mapXvalueHeight 进行如下操作。
{1,加入,一个高度 4},在 mapHeightTimes 中加入(4,1),表示高度 4 出现了 1 次(如果某个高度在 mapHeightTimes 中已经有记录,则只用把次数加 1 即可,在这一步关于高度 4 没有记录,所以新加入即可)。此时在 x=1 处,出现所有高度中的最大高度是 4,将(1,4)记录在 mapXvalueHeight 中,表示在 x=1 处,最大高度是 4。
此时,mapHeightTimes 中所有的记录为:{4,1}。
此时,mapXvalueHeight 中所有记录为:{1,4}。
{2,加入,一个高度 6},在 mapHeightTimes 中加入(6,1),表示高度 6 出现了 1 次。此时在 x=2 处,出现所有高度中的最大高度是 6,将(2,6)记录在 mapXvalueHeight 中,表示在 x=2 处,最大高度是 6。
此时,mapHeightTimes 中所有的记录为:{4,1}, {6,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}。
{3,加入,一个高度 5},在 mapHeightTimes 中加入(5,1),表示高度 5 出现了 1 次。此时在 x=3 处,出现所有高度中的最大高度是 6,将(3,6)记 录在 mapXvalueHeight 中,表示在 x=3 处,最大高度是 6。
此时,mapHeightTimes 中所有的记录为:{4,1}, {6,1}, {5,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}。
{4,加入,一个高度 7},在 mapHeightTimes 中加入(7,1),表示高度 7 出现了 1 次。此时在 x=4 处,出现所有高度中的最大高度是 7,将(4,7)记 录在 mapXvalueHeight 中,表示在 x=4 处,最大高度是 7。
此时,mapHeightTimes 中所有的记录为:{4,1}, {6,1}, {5,1}, {7,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}。
{5,删除,一个高度 6},此时在 mapHeightTimes 中高度 6 只出现了 1 次,又是删除操作,所 以彻底删掉 key=6 的记录(如果出现次数大于 1 次,则把次数减 1 即可,不需要彻底删除)。 此时在 x=5 处,出现所有高度中的最大高度是 7, 将(5,7)记录在 mapXvalueHeight 中,表示在 x=5 处,最大高度是 7。
此时,mapHeightTimes 中所有的记录为:{4,1}, {5,1}, {7,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}。
{6,删除,一个高度 5},此时在 mapHeightTimes 中高度 5 只出现了 1 次,所以彻底删掉 key=5 的记录。此时在 x=6 处,出现所有高度中的最大高度是 7,将(6,7)记录在 mapXvalueHeight 中。
此时,mapHeightTimes 中所有的记录为:{4,1}, {7,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,7}。
{6,删除,一个高度 7},此时在 mapHeightTimes 中高度 7 只出现了 1 次,所以彻底删掉 key=7 的记录。此时在 x=6 处,出现所有高度中的最大高度是 4,将(6,4)记录在 mapXvalueHeight 中。
此时,mapHeightTimes 中所有的记录为:{4,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}。
{7,删除,一个高度 4},此时在 mapHeightTimes 中高度 4 只出现了 1 次,所以彻底删掉 key=4 的记录。此时在 x=7 处,mapHeightTimes 已经空了,所以最大高度是 0,将(7,0)记录在 mapXvalueHeight 中。
此时,mapHeightTimes 中所有的记录为:空。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}。
{9,加入,一个高度 3},mapHeightTimes 中加入(3,1),表示高度 3 出现了 1 次。此时在 x=9 处,出现所有高度中的最大高度是 3,将(9,3)记 录在 mapXvalueHeight 中,表示在 x=9 处,最大高度是 3。
此时,mapHeightTimes 中所有的记录为:{3,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}。
{10,加入,一个高度 5},mapHeightTimes 中加入(5,1),表示高度 5 出现了 1 次。此时在 x=10处,出现的所有高度中的最大高度是 5,将(10,5)记录在 mapXvalueHeight 中,表示在 x=10 处,最大高度是 5。
此时,mapHeightTimes 中所有的记录为:{3,1}, {5,1}。
此时,mapXvalueHeight中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}。
{10,加入,一个高度 2},mapHeightTimes 中加入(2,1),表示高度 2 出现了 1 次。此时在 x=10 处,出现所有高度中的最大高度是 5,将(10,5)记录在 mapXvalueHeight 中,表示在 x=10 处,最大高度是 5。
此时,mapHeightTimes 中所有的记录为:{3,1}, {5,1}, {2,1}。
此时,mapXvalueHeight中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}。
{11,删除,一个高度 3},此时在 mapHeightTimes 中高度 3 只出现了 1 次,所以彻底删掉 key=3 的记录。此时在 x=11 处,出现所有高度中的最大高度是 5,将(11,5)记录在 mapXvalueHeight 中,表示在 x=11 处,最大高度是 5。
此时,mapHeightTimes 中所有的记录为:{5,1}, {2,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}, {11,5}。
{12,加入,一个高度 4},在 mapHeightTimes 中加入(4,1),表示高度 4 出现了 1 次。此时在 x=12 处,出现所有高度中的最大高度是 5,将(12,5),记录在 mapXvalueHeight 中,表示在 x=12 处,最大高度是 5。
此时,mapHeightTimes 中所有的记录为:{5,1}, {2,1}, {4,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}, {11,5}, {12,5}。
{12,删除,一个高度 5},此时在 mapHeightTimes 中高度 5 只出现了 1 次,所以彻底删掉 key=5 的记录。此时在 x=12 处,出现所有高度中的最大高度是 4,将(12,4),记录在 mapXvalueHeight 中,表示在 x=12 处,最大高度是 4。
此时,mapHeightTimes 中所有的记录为:{2,1}, {4,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}, {11,5}, {12,4}。
{13,删除,一个高度 2},此时在 mapHeightTimes 中高度 2 只出现了 1 次,所以彻底删掉 key=2 的记录。此时在 x=13 处,出现所有高度中的最大高度是 4,将(13,4)记录在 mapXvalueHeight 中,表示在 x=13 处,最大高度是 4。
此时,mapHeightTimes 中所有的记录为:{4,1}。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}, {11,5}, {12,4}, {13,4}。
{14,删除,一个高度 4},此时在 mapHeightTimes 中高度 4 只出现了 1 次,所以彻底删掉 key=4 的记录。此时在 x=14 处,mapHeightTimes 已经为空,所以最大高度是 0,将(14,0)记录在 mapXvalueHeight 中,表示在 x=14 处,最大高度是 0。
此时,mapHeightTimes 中所有的记录为:空。
此时,mapXvalueHeight 中所有的记录为:{1,4}, {2,6}, {3,6}, {4,7}, {5,7}, {6,4}, {7,0}, {9,3}, {10,5}, {11,5}, {12,4}, {13,4}, {14,0}。
第五步:根据第四步生成的 mapXvalueHeight 表,生成所有的轮廓线。mapXvalueHeight 表其实统计了在 X 轴上出现的每个点在所有的操作都做完之后,得到的最大高度。轮廓线的产生其实只和每个点最终的最大高度变化有关。下面展示如何根据 mapXvalueHeight 表,生成轮廓线结果数组 res。
{1,4},轮廓线开始产生,开始位置为 1,高度为 4,结束位置待定,目前的最大高度为 4。 res = { {1,待定,4} }。
{2,6},之前的最大高度为 4,现在最大高度变为 6,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 2。同时新的轮廓线开始产生,开始位置为 2,高度为 6,结束位置待定,目前的最大高度为 6。res = { {1,2,4}, {2,待定,6} }。
{3,6},之前的最大高度为 6,现在最大高度仍是 6,所以不产生任何信息。
{4,7},之前的最大高度为 6,现在最大高度变为 7,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 4。同时新的轮廓线开始产生,开始位置为 4,高度为 7,结束位置待定,目前的最大高度为 7。res = { {1,2,4}, {2,4,6}, {4,待定,7} }。
{5,7},之前的最大高度为 7,现在最大高度仍是 7,所以不产生任何信息。
{6,4},之前的最大高度为 7,现在最大高度变为 4,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 6。同时新的轮廓线开始产生,开始位置为 6,高度为 4,结束位置待定, 目前的最大高度为 4。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,待定,4} }。
{7,0},之前的最大高度为 4,现在最大高度变为 0,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 7。根据题目描述,大楼的高度一定大于 0,如果某个位置的最大高度为 0,一定没有高楼,所以没有新的轮廓线开始产生。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,7,4} }。
{9,3},轮廓线开始产生,开始位置为 9,高度为 3,结束位置待定,目前的最大高度为 3。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,7,4}, {9,待定,3} }。
{10,5},之前的最大高度为 3,现在最大高度变为 5,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 10。同时新的轮廓线开始产生,开始位置为 10,高度为 5,结束位置待定,目前的最大高度为 5。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,7,4}, {9,10,3}, {10,待定,5} }。
{11,5},之前的最大高度为 5,现在最大高度仍是 5,所以不产生任何信息。
{12,4},之前的最大高度为 5,现在最大高度变为 4,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 12。同时新的轮廓线开始产生,开始位置为 12,高度为 4,结束位置待定,目前的最大高度为 4。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,7,4}, {9,10,3}, {10,12,5}, {12,待定,4} }。
{13,4},之前的最大高度为 4,现在最大高度仍是 4,所以不产生任何信息。
{14,0},之前的最大高度为 4,现在最大高度变为 0,所以之前结束位置待定的轮廓线,此时可以确定结束位置为 14。根据题目描述,大楼的高度一定大于 0,如果某个位置的最大高度为 0,一定没有高楼,所以没有新的轮廓线开始产生。res = { {1,2,4}, {2,4,6}, {4,6,7}, {6,7,4}, {9,10,3}, {10,12,5}, {12,14,4} }。
最后返回 res 即可。
【代码】
#include (nodes[i].x,maxIter->first));
mapXValueHeight[nodes[i].x] = maxIter->first;
}
}
// res 为结果数组,每一个 vector 代表一个轮廓线,
// 有开始位置、结束位置和高度,一共三个信息
vector<vector<int>> res;
// 一个新轮廓线的开始位置
int start = 0;
// 之前的最大高度
int preHeight = 0;
// 当前位置
int curX = 0;
// 当前最大高度
int curMaxHeight = 0;
// 根据 mapXvalueHeight 生成 res 数组
for (auto iter : mapXValueHeight)
{
curX = iter.first;
curMaxHeight = iter.second;
if (preHeight != curMaxHeight) // 之前最大高度和当前最大高度不一样时
{
if (preHeight != 0)
{
res.push_back(vector<int>({start, curX, preHeight}));
}
start = curX;
preHeight = curMaxHeight;
}
}
return res;
}
};
int main()
{
int n;
scanf("%d", &n);
vector<vector<int>> matrix(n, vector<int>(3));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < 3; j++)
{
scanf("%d", &matrix[i][j]);
}
}
getMatrix *p = new getMatrix();
vector<vector<int>> res = p->buildingOutline(matrix);
for (int i = 0; i < res.size(); i++)
{
cout << endl;
for (int j = 0; j < 3; j++)
{
cout << res[i][j] << " ";
}
}
system("pause");
return 0;
}
加油站良好出发点问题
【题目】
N 个加油站组成一个环形,给定两个长度都是 N 的非负数组 oil 和 dis(N>1),oil[i]代表第 i 个加油站存的油可以跑多少千米,dis[i]代表第 i 个加油站到环中下一个加油站相隔多少千米。假设你有一辆油箱足够大的车,初始时车里没有油。如果车从第 i 个加油站出发,最终可以回到这个加油站,那么第 i 个加油站就算良好出发点,否则就不算。请返回长度为 N 的 bool 型数组 res,res[i]代表第 i 个加油站是不是良好出发点。
例如:
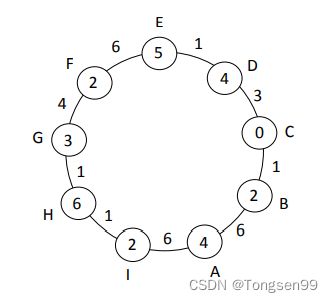
oil = {4, 2, 0, 4, 5, 2, 3, 6, 2}
dis = {6, 1, 3, 1, 6, 4, 1, 1, 6}
代表的图如图所示。
图中 A 点油量为 oil[0],A 点到 B 点距离为 dis[0];B 点油量为 oil[1],B 点到 C 点距离为 dis[1]……I 点油量为 oil[8],I 点到 A 点距离为 dis[8]。如果从 A 点出发,车初始将获得 4 的油量,但是 A 到 B 距离为 6,车跑不到 B 就会停下,所以 A 不是良好出发点;如果从 B 点出发,车初始将获得 2 的油量,B 到 C 距离为 1,车可以跑到 C,并且还剩 1 的油量,C 点油量为 0,所以车仍然带着 1 的油继续往下走,但是 C 到 D 距离为 3,车跑不到 D 就会停下,所以 B 也不是良好出发点;如果从 C 点出发……这个例子没有任何一个点是良好出发点,所以返回{false, false, false, false, false, false, false, false, false}。
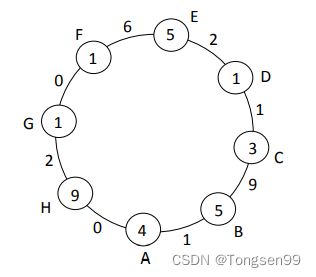
oil = {4, 5, 3, 1, 5, 1, 1, 9}
dis = {1, 9, 1, 2, 6, 0, 2, 0}
代表的图如图所示。
如果从车 A 点出发,到 B 点且加上 B 的油,还剩 8 的油,发现到不了 C;如果从 B 点出发,发现车到不了 C;如果从 C 点出发,发现可以转一圈,所以 C 点是良好出发点……最终返回{false, false, true, false, false, true, false, true}。
【解答】
-
预处理+双指针
首先可以把数据经过简单处理,oil[i]-dis[i]可以表示从 i 位置走到下一个位置,但是还没有加下 一个位置的油量之前剩余的油量。比如题目描述的例子中,例子一可以用下图表示。

例子二可以用下图表示。

那么考查某个点是否是良好出发点的标准就可以变为,从该点出发转一圈沿途累加所有的数字,如果重新转回该位置的过程中累加和一直不小于 0,说明这个点是良好出发点,否则就不是。得到每个位置的 oil[i]-dis[i]值的数组,可以选择修改 dis 数组的方式来实现。
预处理之后,dis[i]就变成了原来的 oil[i]-dis[i]值,我们把新的 dis 数组认为是“纯能数组”,同时预处理操作需要返回一个纯能值大于或等于 0 的位置,我们把这个点叫作环的 init 点,只要是纯能值大于或等于 0 的位置都可以作为 init 点,选择哪一个都行。比如,例子一中的 B、D、G 和 H 点,例子二中的 A、C、F 和 H 点。下面的过程是依次考查 init 点以及从 init 点顺时针方向遇到的每一个点是否是良好出发点。假设例子一的 H 点作为 init 点,例子二的 A 点作为 init 点。
前提:init 点存在。如果 init 点不存在,说明所有的加油站纯能值都小于 0,那么必然所有点都不是良好出发点,直接返回结果即可。在满足前提的情况下,进入步骤一。
步骤一:扩充连通区。
连通区表示为[start,end),这里使用[)符号并不是指数学上值的范围是左闭右开,而是说车在初始时是从 start 位置出发的,沿着逆时针行进,可以达到 end 位置的前一个位置。need 值为从 start 位置顺时针扩充连通区的要求,rest 值为从 end 位置逆时针扩充连通区的资源。在查看每一个点是否是良好出发点的过程中,通过 need 值和 rest 值的变化来扩充连通区。下面以例子一来说明。
init 点为 H 点,从这个点开始考查。目前连通区为[H,I),need=0,rest=5。因为此时 rest=5,I 位置的纯能值为-4,所以连通区扩为[H,A),rest 变为 1。A 位置的纯能值为-2,而 rest=1 说明 A位置逆时针扩充连通区的资源不足,所以扩充停止。连通区并没有扩充到整个环,所以 H 点不是良好出发点。
开始考查 G 点。目前连通区为[H,A),need=0,rest=1。因为 G 点的纯能值为 2,need=0,说明从 H 位置顺时针扩充连通区的要求满足,所以连通区扩为[G,A),并且 G 点的纯能值为 2,即可以满足要求。另外,可以把多出来的 2 点纯能带到连通区域的最后,增加从 A 位置逆时针扩充连通区的资源,所以 rest=1+2=3。A 位置的纯能值为-2,所以连通区扩为[G,B),rest 变为 1。B 位置的纯能值为 1,说明不仅可以扩充,还能增加 rest 值,所以连通区扩为[G,C),rest=2。C位置的纯能值为-3,资源不够,所以扩充停止,连通区并没有扩充到整个环,所以 G 点不是良好出发点。
开始考查 F 点。目前连通区为[G,C),need=0,rest=2。因为 F 点的纯能值为-2,不满足从 G位置顺时针扩充连通区的要求,所以连通区不发生任何变化,并且 need 应该变为 2。因为之后要想从 G 位置顺时针扩充连通区,是一定要通过 F 点的。连通区并没有扩充到整个环,所以 F点不是良好出发点。
开始考查 E 点。目前连通区为[G,C),need=2,rest=2。因为 E 点的纯能值为-1,不满足从 G位置顺时针扩充连通区的要求。所以连通区不发生任何变化,并且 need 应该变为 3。连通区并没有扩充到整个环,所以 E 点不是良好出发点。
开始考查 D 点。目前连通区为[G,C),need=3,rest=2。因为 D 点的纯能值为 3,need=3,说明从 G 位置顺时针扩充连通区的要求满足(D 确实可以经过 E、F 达到 G),所以连通区扩为[D,C),并且 D 点的纯能值为 3,即可以满足要求。另外,可以把多出来的 0 点纯能带到连通区域的最后,增加从 C 位置逆时针扩充连通区的资源,所以 rest 依然为 2。C 点的纯能值为-3,所以扩不动了,并且 need 应该变成 0,因为之后要想从 D 位置顺时针扩充连通区,只要新到节点的纯能值不小于 0 即可。
开始考查 C 点。目前连通区为[D,C),need=0,rest=2。因为 C 点的纯能值为-3,不满足从 D位置顺时针扩充连通区的要求。所以连通区不发生任何变化,并且 need 应该变为 3。连通区并没有扩充到整个环,所以 C 点不是良好出发点。
此时发现接下来的考查点都已经在连通区里,并且在之前没有发现任何一个良好出发点,那么可以证明剩下的点一定都不是良好出发点,如下图所示。
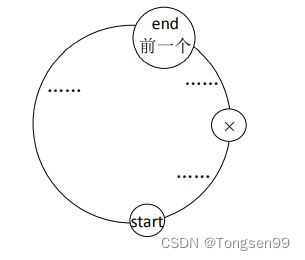
证明:假设连通区是图中从 start 开始逆时针到 end 前一个,并假设 X 点是此时的考查位置。如果 X 点的纯能值小于 0,X 一定不是良好出发点。如果 X 点的纯能值大于或等于 0。根据连通区的定义,从 start 出发可以来到 end 前一个位置,那么在从 start 出发的情况下,一定可以达到 X 点,在累加 X 点的纯能值之前,所带的资源一定是大于或等于 0 的(不然不可能走到 X)。那么在累加了 X 点的纯能值之后,资源一定会大于或等于 X 点的纯能值,但即便是在这种状况下,都没有走到 end 位置。那么如果车初始时是从 X 出发的,资源就是 X 点的纯能值,就更不可能走到 end 位置,也就不可能转一圈,所以 X 一定不是良好出发点。所以例子中的后续过程不需要考查 B、A,它们一定不是良好的出发点。
上面的例子(题目描述的例子一)展示了在考查每一个点时,如果一直没有发现良好出发点的情况下,该如何处理。接下来的例子展示如果在考查的过程中,发现了哪怕一个良好出发点,该怎么处理。下面以例子二来说明。
init 点为 A 点,从这个点开始考查。目前连通区为[A,B),need=0,rest=3。因为 B 点的纯能值为-4,资源不够,所以扩充停止,连通区并没有扩充到整个环,所以 A 点不是良好出发点。
开始考查 H 点。目前连通区为[A,B),need=0,rest=3。因为 H 点的纯能值为 9,need=0,说明从 A 位置顺时针扩充连通区的要求满足,所以连通区扩为[H,B),并且可以把多出来的 9 点纯能带到连通区域的最后,增加从 B 位置逆时针扩充连通区的资源,所以 rest 变为 12。接下来发现,连通区可以扩到整个环,也就是可以回到 H 点,那么 H 是一个良好出发点。接下来的过程将变得很简单,如下图所示。
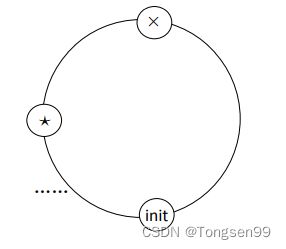
我们从上图的 init 位置开始顺时针考查每一个点是否是良好开始点,如果我们在标记星号的位置时发现星号位置是良好开始点。假设从星号继续顺时针遇到的 init 之前的每一个点,记为 X。因为从星号出发可以转一圈,所以 X 只要能达到星号位置,X 一定可以转一圈。
至此,已经穷举了所有的可能性。考查每一个点的过程中,连通区都可能会扩大,但是一旦扩到整个环,或者考查节点来到连通区,后续的过程都将没有连通区的扩大过程。
【代码】
#include 容器盛水问题
【题目】
给定一个数组 arr,已知其中所有的值都是非负的,将这个数组看作一个容器,请返回容器能装多少水。
例如,arr = {3,1,2,5,2,4},代表的容器如下图所示。
该容器可以装下 5 格水,也就是图中画圈的部分,所以返回 5。
arr = {4,5,1,3,2},代表的容器如下图所示。
该容器可以装下 2 格水,也就是图中画圈的部分,所以返回 2。
【解答】
-
法一:预处理数组
把数组中值的变化趋势想象成波峰和波谷的变化,然后试图找到所有的波谷,那么波谷里一定会有水,把所有波谷的水累加起来就是答案。
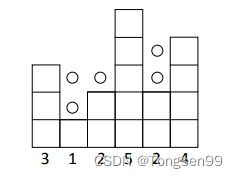
比如,数组[4,3,1,4,7,6,3,0,6],代表的容器如下图所示,容器的两个阴影部分代表两个波谷,也是可以装水的部分。这种想法看起来非常靠谱,但是很明显找到所有的波谷后再求其中水的格子数量编程难度不小,而且遍历过程中发现的波谷有失效的情况。

比如,数组[9,2,4,1,6,2,8,4,9],代表的容器如下图所示。
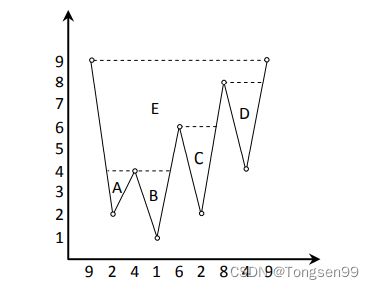
在从左到右遍历图中数组的过程中,会依次出现 A、B、C、D 四个波谷,但它们都会失效,因为整个数组就是一个大容器,所有的小波谷都是整个大波谷 E 的一部分。所以划分波峰和波谷的想法不仅难以实现,而且要考虑很多复杂的情况。
下面介绍一个简洁的标准。如果现在来到 i 位置,只单独考虑 i 位置的上方能有几格水。
假设 arr[i]=4,如果 i 位置左侧所有数(arr[0…i-1])的最大值为 10,右侧(arr[i+1…N-1])的最大值为 20,那么 i 位置上方的水一定能够到达高度为 10 的地方,再高的话一定会从左侧流走,所以有 6 格水。同理,如果左侧最大值为 12,右侧最大值为 6,那么 i 位置上方的水一定能够到达高度为 6 的地方,再高的话一定会从右侧流走,所以有 2 格水。
假设 arr[i]=4,如果 i 位置左右两侧的最大值有一个小于或等于 4,那么 i 位置上方的水一定会从某侧流走,所以有 0 格水。
这个标准的简洁表达为: i 位置上方水的数量 = max{ min{ i 左侧的最大值,i 右侧的最大值 } - arr[i] , 0 }。如果我们依次求出数组中每一个位置上方的水,都累加起来就是答案。
对于求 i 位置两侧最大值可以通过遍历的方式,这里有一个优化,即用预处理数组的方式减少遍历的代价。
生成和 arr 等长的两个数组 leftMaxs 和 rightMaxs,leftMax[i]的含义是 arr[0…i]的最大值,rightMaxs[i]的含义是 arr[i…N-1]的最大值,比如 arr=[3,1,5,6,7,6,3],从左往右遍历生成 leftMaxs,leftMaxs[i]=max{leftMaxs[i-1], arr[i]},得到 leftMaxs=[3,3,5,6,7,7,7]。从右往左遍历生成 rightMaxs,rightMaxs[i]=max{rightMaxs[i+1], arr[i]},得到 rightMaxs=[7,7,7,7,7,6,3]。很明显,arr 生成两个预处理数组只需遍历两次,之后对于任何一个 i 位置,左侧的最大值就是 leftMax[i-1],右侧的最大值就是 rightMax[i+1]。
【代码】
- 法一
#include -
法二:双指针
还可以对过程中使用的数组做优化,设置左右两个指针,记为 L 和 R,还有两个变量 leftMax 和 rightMax,初始时 L 指向 arr[1]的位置,R 指向 arr[N-2]的位置, leftMax=arr[0],rightMax=arr[N-1],一共就这 4 个变量。求解每一步让 L 向右移动或者 R 向左移动,leftMax 表示 arr[0…L-1]中的最大值,rightMax 表示 arr[R+1…N-1]中的最大值,如下图所示。

1)如果 leftMax 小于或等于 rightMax,此时可以求出 L 位置上方的水量。这是因为 rightMax 是 arr[R+1…N-1]的最大值,而 L 的右侧还有一个未遍历的区域,所以 L 右侧最大值一定不会小于 rightMax。leftMax 代表 L 左侧的最大值,此时的假设又是 leftMax 小于或等于 rightMax,所以可知左侧最大值 leftMax 是 L 位置的瓶颈。故 L 位置上方的水量=Max{leftMax - arr[L],0}。然后让 L 向右移动,在移动之前 leftMax 要更新。(leftMax=Max{leftMax, arr[L++]})
2)如果 leftMax 大于 rightMax,此时可以求出 R 位置上方的水量。解释与情况1)同理,R 位置上方的水量=max{rightMax - arr[R],0}。然后让 R 向左移动,在移动之前 rightMax 要更新。(rightMax=Max{rightMax, arr[R–]})
3)每一步都会求出 L 或者 R 一个位置的水量,把这些水量都累加起来,当 L 和 R 相遇之后一旦错过(L > R),过程就结束。
【代码】
- 法二
#include