SNARK Design

1. 引言

主要参考Justin Thaler 2022年8月在a16z crypto专题研讨会上的系列讲座：

• SNARK Design, Part I, with Justin Thaler | a16z crypto research talks
• SNARK Design, Part II, with Justin Thaler | a16z crypto research talks
• SNARK Design Part III with Justin Thaler | a16z crypto research talks

1.1 何为SNARK？

SNARK针对的场景为：
Prover $P$声称其知道满足某属性的witness $w$，如：

• 某原像$w$，使得其哈希结果为指定的$y$，即$h(w)=y$【Prover和Verifier均已知哈希函数$h$和哈希结果$y$，$w$为wtiness仅Prover已知】。
• 某私钥$w$，使得其对应某密码学系统指定的公钥，即$\text{Public\_key}(w)=y$。【Prover和Verifier均已知公钥$y$和相应的公钥计算规则$\text{Public\_key}$，$w$为wtiness仅Prover已知】。

最简单直接的证明方式为：

• Prover $P$将$w$直接发送给Verifier $V$，$V$对其运算验证是否满足所声称的属性。

SNARK（全称为Succinct Non-interactive ARgument of Knowledge）可实现同样的效果，但其对Verifier更友好——验证证明的开销更小：【由于当前Rollup重点关注可扩展性而不是隐私性，其无需zero-knowledge SNARK，因此本文未添加ZK字段。当前的Rollup，与其称是zk-Rollup，不如说是validity-Rollup。】

• SNARK证明$\pi$的长度要比 witness $w$短——即对应为“Succinct”；
• 验证$\pi$证明 的速度 要快于 基于$w$直接运算——即节约Verifier $V$的计算开销。

1.2 本文基本结构

本文基本结构为：

• 1）SNARK设计原理：
  • SNARK前端和后端设计
  • SNARK后端设计：polynomial IOPs和多项式承诺方案
• 2）SNARK分类及优劣势分析
• 3）何为（validity-）Rollup以及现有Rollup项目总览
  • 性能及安全考量
• 4）示例：
  • polynomial IOP示例和多项式承诺示例
  • 并揭露这些示例的核心思想

2. SNARK设计原理

2.1 通用SNARK：标准范式

首先针对以高级编程语言（C/Java等）编写的计算程序：

• 仍以之前的pre-image hash为例：程序以$w$为输入，对其执行$h$函数，然后检查程序输出等于$y$。

通用SNARK的标准范式为：

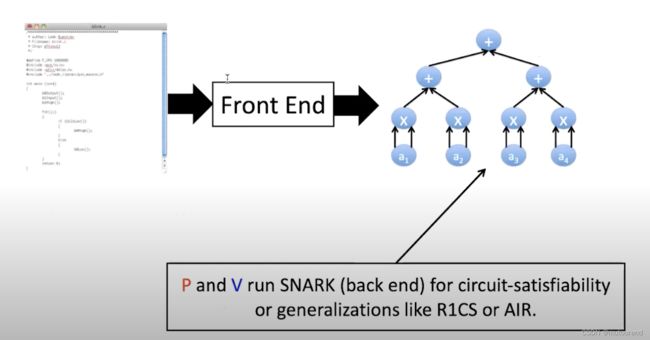
• 1）Step 1（前端转换）：将程序转换为等价的amendable probabilistic check：
  • 通常转换为某种circuit-satisfiability 或 R1CS；
  • 这称为SNARK系统的前端。
• 2）Step 2（后端证明）：为circuit-satisfiability/R1CS 运行SNARK生成证明：
  • 这称为SNARK系统的后端。
  • 相应的SNARK后端有，如：Groth16、Marlin、PlonK、Ligero、Hyrax、Libra、Virgo、Brakedown、Supersonic等等。

2.2 SNARK后端设计的关键范式

SNARK系统后端的目标为：

• 为circuit-SAT or R1CS选择某种SNARK方案，使得：
  • 1）$P$ 运行尽可能为linear-time。
  • 2）Proof size应尽可能小：
    • 理想情况下应仅为数百字节 或 几kB。
  • 3）$V$ 验证应尽可能快：
    • 理想情况下，$V$可读取任意的public input，并仅需要几毫秒就可完成proof验证。
  • 4）理想情况下，应为Transparent的（无需trusted setup从而不引入“toxic waste”）。【仅取决于多项式承诺方案，与Polynomial IOP无关】
  • 5）理想情况下，应具有Plausibly post-quantum secure。【仅取决于多项式承诺方案，与Polynomial IOP无关】

（基于“linear-PCP”的SNARK方案（如GGPR13、Pinocchio、Groth16等）除外），当前所有transparent 和 “universal trusted-setup” SNARK后端设计的关键范式在于：【即使基于linear-PCP的SNARK方案也会采用类似的特定多项式承诺方案（KZG）。】

• 1）为R1CS or circuit-satisfiability指定某“polynomial IOP”；
• 2）与 某多项式承诺方案 结合，实现succinct interactive argument；
• 3）通过Fiat-Shamir transformation将interactive 转换为 non-interactive。

2.3 何为Polynomial-IOP？

在Polynomial-IOP协议中：

• $P$的第一个message为多项式$h$：
  • $V$无需知道整个多项式$h$，原因在于：
    • 描述多项式$h$的size 与 整个circuit 一样大。
  • 转而为，$V$可evaluate $h$ at 某 point。
  • 然后，$P$和$V$运行标准的interactive proof。

2.4 何为多项式承诺方案？

从高层来看，多项式承诺方案的核心思想为：

• $P$通过发送某short string $Com(h)$来 bind to 多项式$h$；【承诺具有绑定属性】
• $V$选择$x$，并请求$P$ evaluate $h(x)$；
• $P$发送$y$为声称的$h(x)$ evaluation值，同时附加一个证明$\pi$——表明$y$值与$Com(h)$和$x$一致。

多项式承诺方案的目的在于：

• $P$无法为错误的evaluation值生成convincing proof；
• $Com(h)$和$\pi$应简短且易生成；
• $\pi$应易于验证。

3. SNARK分类

当前有多种不同的polynomial IOP和多项式承诺方案，二者进行不同的组合，可在：

• $P$ time
• proof size
• setup assumption

等方面做不同的权衡取舍。其中Transparent和Plausibly post-quantum secure 属性 仅取决于多项式承诺方案，与Polynomial IOP无关。

3.1 Polynomial IOP分类

当前的Polynomial IOP主要分为三大类：

• 1）基于interactive proofs（IPs）的Polynomial IOP：如Hyrax、vSQL、Libra、Virgo等。【$P$无需做FFT运算】
• 2）基于multi-prover interactive proofs（MIPs）的Polynomial IOP：如Spartan、Brakedown、Xiphos等。【$P$无需做FFT运算】
• 3）基于constant-round的Polynomial IOP：如Marlin、PlonK、StarkWare的SNARKs等。【$P$需要做FFT运算】

以上方案都是通过增加$P$开销，来减少proof长度以及降低$V$开销。
以上1）2）类，只要其结合的多项式承诺方案也不需要FFT，则$P$无需做FFT运算。

3.2 多项式承诺方案分类

当前的多项式承诺方案主要分为四大类：

• 1）基于pairing的多项式承诺方案（既不transparent，也不post-quantum）
  • 如KZG10、PST13、ZGKPP18等。
  • 独特属性有：具有constant sized evaluation proofs。
• 2）基于discrete logarithm的多项式承诺方案（transparent，但不post-quantum）
  • 如BCCGP16、Bulletproofs、Hyrax、Dory等。【其中Dory即需要discret-log hardness，还需要pairing。】
• 3）基于IOPs+hashing（transparent 且 post-quantum）
  • 如Ligero、FRI、Brakedown等。
• 4）基于Groups of unknown order的多项式承诺方案（若使用class groups具有transparent属性，但不是post-quantum的）
  • 如DARK、Dew等。
  • 由于使用class groups，$P$非常慢。

3.3 SNARK分类及优劣势分析

3.3.1 non-transparent SNARK分类及优劣势分析

non-transparent SNARK方案分类有：

• 1）基于Linear-PCP的SNARK方案：
  • 如Groth16等。
  • 优势：具有最短的proof size（3个group elements）和 最快的$V$。
  • 劣势：需要circuit-specific trusted setup，具有slow且space-intensive的$P$，不是post-quantum的。
• 2）constant-round polynomial IOP + KZG多项式承诺 组成的SNARK方案：
  • 如Marlin、PlonK等。
  • 优势：Universal trusted setup。
  • 劣势：Proof size要比Grouth16大约4~6倍，$P$要比Groth16慢，且不是post-quantum的。
    • $P$可采用比 circuits和R1CS 更灵活的intermediate representations。

3.3.2 transparent SNARK分类及优劣势分析

transparent SNARK方案分类有：

• 3）MIPs 和 IPs + [fast-prover多项式承诺] 组成的SNARK方案：
  • 如Spartan、Brakedown、Xiphos、Hyrax等。
  • 优势：论文上说具有 fastest $P$，若相应的多项式承诺是plausibly post-quantum+transparent的，则还具有plausibly post-quantum+transparent属性。
  • 劣势：Proof size要比以上 [基于Linear-PCP的SNARK方案] 和 [constant-round polynomial IOP + KZG多项式承诺 组成的SNARK方案] 的proof size要大。
• 4）[任意polynomial IOP] + FRI多项式承诺 组成的SNARK方案：
  • 如Fractal、Aurora、Virgo、Ligero++等。
  • 优势：在所有plausibly post-quantum SNARK方案中，具有最短的proof。
  • 劣势：Slow $P$，proof size仍相对较大。

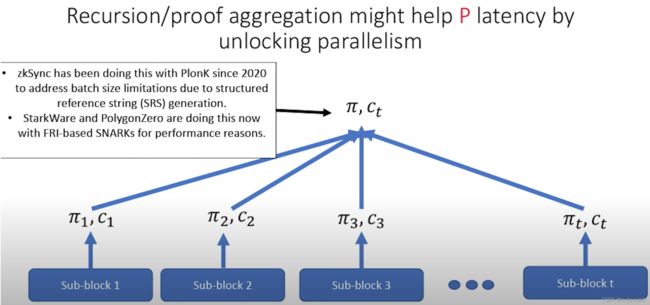
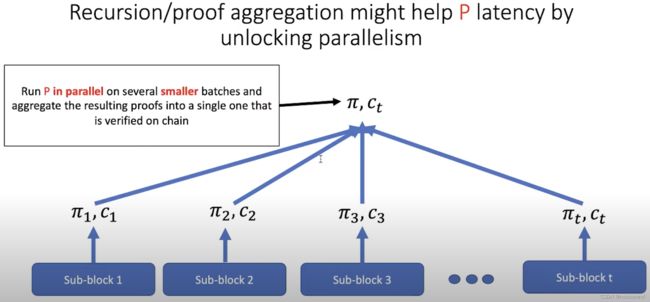
3.4 进行时：通过组合来实现最好的SNARK？

通过将“fast prover, big proof” SNARK方案 与 “small proof” SNARK方案 组合使用：【这种组合方式对于Rollup场景来说，是有吸引力的。】

• $P$不直接将“big proof” $\pi$发送给$V$；
• 而改为：$P$ proves that it knows $\pi$ using the small-proof SNARK。

相应的：

• 最终的proof size和$V$ time取决于“small proof” SNARK方案。
• 同时，要求“big proof” SNARK方案具有proof efficiency。
• 还需要将“big proof” SNARK verifier以电路表示，将该电路用于“small proof” SNARK中。

4. 以太坊现有Rollup项目总览

4.1 Rollup Context

Rollup项目产生的背景在于：

• 1）公链中弱节点也应可参与验证：
  • Extreme Bitcoin-community ehtos为：“Not your node, not your validation”。
  • Less extreme：若大多数以太坊节点都运行在AWS服务器上，Amazon可毁掉以太坊网络。
• 2）运行节点的开销主要有2方面：
  • 2.1）验证交易时的计算开销：
    • 2.1.1）对于转账交易，计算开销主要在于：验签和检查account balances。
    • 2.1.2）对于通用以太坊交易，可能会执行任意EVM bytecode。【以Solidity高级语言编写智能合约，然后将合约编译为EVM（Ethereum Virtual Machine）bytecode，以太坊节点将运行这些bytecode。】
  • 2.2）下载、存储、访问链上所有数据的开销 ：
    • 可将这些数据称为“the state of the world（世界状态）”。
    • 可将其看成是所有用户的ETH account balances。

Rollup思路一是：

• 将链看成是计算能力较弱的$V$，而将rollup服务看成是untrusted $P$，从而：
  • 可节约链上节点的计算开销：
    • 如，不需要直接验证签名，仅需要验证某proof，该proof若验证通过，则所有链上交易的签名都是有效的。
  • 并不直接减少/压缩链上的数据量。
• 将链称为“layer 1（L1）”或“the chain”，将rollup称为“layer 2（L2）”。

Rollup思路二为：

• 不将“state of the world”存储在链上，仅将相应的commitment存储上链：
  • 如，在链上存储 a Merkle-hash of all account balances。
• commitment的binding属性，可确保没人可“alter修改”该数据：
  • 任何成功"authenticate"某数据片段与该commitment一致的人，均需展示真实的数据。即无人可篡改数据并对应同一commitment值。
• 关键结论：
  • 不再需要依赖链上共识机制来确保无人可篡改数据。

对于data availability（数据可用性，即，被commit的数据对rollup provider之外的任何人都可用，以确保当provider跑路了，整个rollup服务的liveness仍可保证），针对Rollup思路二，有2种数据可用性备选方案：

• 1）仍将数据存储在链上，以确保可用性：
  • 存在名为CALLDATA的cheaper storage，仅由全节点存储；
  • 以太坊正在考虑将本备选方案搞得更具可扩展性：
    • EIP4444将让链上CALLDATA数据在一年后过期。
    • Sharding分片将增加链上存储量。
  • 由于数据存储在链上，rollup的优势是有限制的。
• 2）采用经济激励模式，使得链下实体来参与存储数据并保证数据可用性。

将以上思路一和思路二结合起来，Rollup的工作原理可为：

• 1）尝试一：
  • 任何时候，都将世界状态的承诺值存储在L1。
  • rollup运行一组交易后获得新的世界状态，会将新的世界状态的承诺值提交到L1。
  • 问题在于：L1如何知道新的承诺值是正确的？
  • 相应的解决方案为：rollup在提交新的承诺值的同时，会附加一个SNARK proof $\pi$来证明新承诺值的正确性：
    • 基于初始状态，应用一组交易之后，获得的结束状态，以及所有交易都是有效的（签名正确、无negative balances等）。
    • $\pi$必须在链上验证：所有的区块链节点都需运行该proof的SNARK verifier。

4.1.1 数据可用性的衍生讨论

关于数据可用性的衍生讨论：

• 是否可由除rollup service之外的其它实体来提交proof，来推动系统状态的变化？
  • 若不支持，需考虑centralization和censorship。
  • 若支持（或当service compromised时），如何来避免如下“data availability attack”？
    • 1）为某些合法的交易honestly生成proof，但是，却不告知其他人这些交易具体内容（或者告知他人错误的交易数据）。
    • 2）更新链上承诺值，但每人知道该承诺值对应的全量数据。
    • 3）liveness被架起：无法对该承诺值进一步更新，因为$P$需要知道承诺值底层的数据，或者至少需要知道Merkle tree中除root commitment值之外的多个哈希值（任何交易都至少可修改其中一个哈希值）。

避免数据可用性攻击的解决方案可为：

• 1）借助链上存储：$V$（为链上合约）要求将所有state changes作为CALLDATA。
  • 若naively实现，将增加$V$开销，因需将这些state changes作为“SNARK verification”流程的输入。对于每个变化了的account，这需要昂贵的密码学运算。
  • 借助[SL20]的“hash trick”可降低开销：
    • 仅将state changes的哈希结果$h$作为SNARK的输入；
    • $V$可在“SNARK verification”流程之外，检查该哈希结果$h$确实为某些CALLDATA的哈希值。
• 2）借助链下存储：（如存储在某些BFT系统中）
  • BFT系统可对state changes的哈希结果$h$进行门限签名，以证实其存储了该state changes；
  • $V$在将$h$作为 提交到L1上proof 输入 之前，需获取$h$的BFT门限签名；
  • 从而将Rollup liveness reduce为 BFT系统liveness。

4.2 Rollup性能分析

Rollup性能分析时，关注的指标有：

• 1）Latency延迟：即交易提交到L2 与 L1上获得该交易proof 之间的时间延迟，这取决于：
  • $P$ time
  • ➕ 多久可等到足够的交易数量使得L2会打包一个batch。
• 2）Throughput吞吐量：即指定时间内，rollup可处理的L2交易总数：
  • 假设某人可在$Y$秒内 upload $X$笔交易对应的proof 到 L1。
  • 且每$Y$秒内，都有足够的$X$笔交易在L2上产生：
    • 则，每$Y$秒可向$P$发送一个新的batch，同时，向L1提交最新完成的proof。
    • 持续这种稳定状态的情况下，每$Y$秒可向L1提交 包含了$X$交易的proof。
    • 相应的吞吐量计算为：$X/Y$ transactions/second（TPS）。
    • 这与latency（$P$ time）无关，仅包含了$V$ costs：更准确来说，是$V$ costs 与 batch size 之间的比率值。
    • 吞吐量决定了“链的可扩展性”。
    • 但是实际上，延迟（Latency）将限制batch size，从而影响吞吐量。

当前很多Rollup项目在介绍其性能时，通常会忽略延迟（Latency）指标，而侧重于只介绍吞吐量（TPS）。
zkRollup（validity-rollup）之外的其他备选rollup方案，通常具有高延迟：

• Optimistic Rollup：约7天
• Visa：约48小时

通常终端用户并不承担因延迟导致的风险，如：

• 中心化exchange可能会为用户迅速固化交易，但有exchange本身来承担交易在L1上固化出问题的风险。

通过解锁并行化，借助Recursion/proof aggregation，可能可帮助$P$降低延迟：