qiuzitao机器学习(一):吴恩达机器学习梯度下降
(一)qiuzitao3.25-3.30学习报告
3.25(周一)
机器学习的第一篇博客,接下来也会坚持更新,谢谢我的导师和CSDN这个平台!
#吐槽一下这学期课很多,学费值了;开的语言也多(Python,Java,C++,汇编),不过我钟爱Python和Java,更有兴趣的还是机器学习,人工智能。
晚上回顾了Python的文件语法,现在的Python算基础掌握了吧,也是入了这个门,还需要多练习提升,打打代码。
文件切割术(把record.txt按要求切割成boy_1.txt boy_2.txt boy_3.txt girl_1.txt1 girl_2.txt girl_3.txt)


3.26(周二)
总结:吴恩达机器学习第一章
一:监督学习
1.回归问题
给定的一个房子的面积来预测这个房子在市场中的价格. 这里的房子的面积就是特征, 房子的价格就是一个输出值. 为了解决这个问题, 我们获取了大量的房地产数据, 每一条数据都包含房子的面积及其对应价格. 第一, 我们的数据不仅包含房屋的面积, 还包含其对应的价格, 而我们的目标就是通过面积预测房价. 所以这应该是一个监督学习; 其次, 我们的输出数据房价可以看做是连续的值, 所以这个问题是一个回归问题。
2. 分类问题
目标应该是要对数据进行分类.。比如我们的数据是有关乳腺癌的医学数据, 它包含了肿瘤的大小以及该肿瘤是良性的还是恶性的. 我们的目标是给定一个肿瘤的大小来预测它是良性还是恶性. 我们可以用0代表良性,1代表恶性, 这就是一个分类问题。 因为我们要预测的是一个离散值.
在这个例子中特征只有一个即瘤的大小。 对于大多数机器学习的问题, 特征往往有多个(上面的房价问题也是, 实际中特征不止是房子的面积). 例如下图, 有“年龄”和“肿瘤大小”两个特征。
二:无监督学习
2.1 新闻分类
Google News搜集网上的新闻,并且根据新闻的主题将新闻分成许多簇, 然后将在同一个簇的新闻放在一起。如图中红圈部分都是关于BP Oil Well各种新闻的链接,当打开各个新闻链接的时候,展现的都是关于BP Oil Well的新闻。
2.2 根据给定基因将人群分类
给一组DNA数据,对于一组不同的人我们测量他们DNA中对于一个特定基因的表达程度。然后根据测量结果可以用聚类算法将他们分成不同的类型。
2.3 鸡尾酒派对效应
*机器学习定义:
对于一个程序,给它一个任务T和一个性能测量方法P,如果在经验E的影响下,P对T的测量结果得到了改进,那么就说该程序从E中学习**
| 分 类 | 内 容 | 例 子 |
|---|---|---|
| 监督学习 | 回归 在已有数据中找规律,解决类似问题 | 预测房价 |
| 无监督学习 | 聚类,独立组件分析寻找混合数据之间的区别进行分类 | 区分声音 |
| 强化学习 | 回报函数,自我学习优化算法。 | 机器人运动 |
作业软件:Matlab/Octave
3.27-3.28(周三-周四)
代价函数cost function
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y i ~ − y i ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(θ_0,θ_1)= \frac{1}{2m} \displaystyle\sum_{i=1}^{m} (\tilde{y_i}−y_i)^2=\frac{1}{2m} \displaystyle\sum_{i=1}^{m} (h_θ({x_i})−y_i)^2 J(θ0,θ1)=2m1i=1∑m(yi~−yi)2=2m1i=1∑m(hθ(xi)−yi)2
这个函数被称为“平方误差函数”或“均方误差”。
平方项求导有常数2,增加1_2系数,以方便计算梯度下降。
示例:
假设(hypothesis): h θ ( x ) = θ 0 + θ 1 x h_θ(x)=θ_0+θ_1x hθ(x)=θ0+θ1x
参数(parameter): θ 0 , θ 1 θ_0,θ_1 θ0,θ1
代价函数(cost function):
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( y i ~ − y i ) 2 = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 J(θ_0,θ_1)= \frac{1}{2m} \displaystyle\sum_{i=1}^{m} (\tilde{y_i}−y_i)^2=\frac{1}{2m} \displaystyle\sum_{i=1}^{m} (h_θ({x_i})−y_i)^2 J(θ0,θ1)=2m1i=1∑m(yi~−yi)2=2m1i=1∑m(hθ(xi)−yi)2
对于多变量还可以写做: J ( θ ) = 1 2 m ( X θ − y ⃗ ) T ( X θ − y ⃗ ) J(θ)=\frac{1}{2m}(X_θ−y⃗ )^T(X_θ−y⃗ ) J(θ)=2m1(Xθ−y⃗)T(Xθ−y⃗)
目标(goal): minimize J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)
梯度下降(gradient descent)
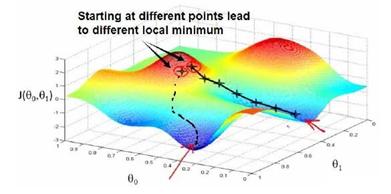
梯度下降背后的思想是:开始时我们随机选择一个参数的组合( θ 0 θ 0 , θ 1 θ 1 , … , θ n θ n θ_0θ_0, θ_1θ_1,…,θ_nθ_n θ0θ0,θ1θ1,…,θnθn ),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值。
批量梯度下降(batch gradient descent)算法的公式为:

α 是学习速率,步伐大小,α 后面的全部是导数项。

导数值(斜率)越来越小即 α α θ \frac{α}{αθ} αθα越来越小
对线性回归运用梯度下降法

对之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即:


则算法改写成:

3.29(周五)
梯度下降练习
import sys
#Training data set
#each element in x represents (x1)
x = [1,2,3,4,5,6]
#y[i] is the output of y = theta0+ theta1 * x[1]
y = [2,4,6,8,10,12]
#设置允许误差值
epsilon = 0.0001
#学习率
alpha = 0.01
diff = [0,0]
max_itor = 999
error1 = 0
error0 =0
cnt = 0
m = len(x)
#init the parameters to zero
theta0 = 0
theta1 = 0
while 1:
cnt=cnt+1
diff = [0,0]
for i in range(m):
diff[0]+=theta0+ theta1 * x[i]-y[i]
diff[1]+=(theta0+theta1*x[i]-y[i])*x[i]
theta0=theta0-alpha/m*diff[0]
theta1=theta1-alpha/m*diff[1]
error1=0
for i in range(m):
error1+=(theta0+theta1*x[i]-y[i])**2
if abs(error1-error0)< epsilon:
break
print('theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1))
if cnt>999:
print ('cnt>999')
break
print('theta0 :%f,theta1 :%f,error:%f'%(theta0,theta1,error1))
通过修改误差值epsilon=0.0001,增加迭代次数到999次,theta0的值越来越接近0.5,theta1的值越来越接近2。运行结果如下:

优化学习率
调整学习率: 在斜率(方向导数)大的地方,使用小学习率,在斜率(方向导数)小的地方,使用大学习率。
def get_A_Atmiho(x,d,a):
c1=0.3
now=f(x)
next=f(x-a*d)
#下面的循环是寻找最大的步长a,使得目标函数可以向减小的方向移动
count=30
while nextnow-c1*a*d**2:
a=a/2
next=f(x-a*d)
count-=1
if count==0:
break
return a;
