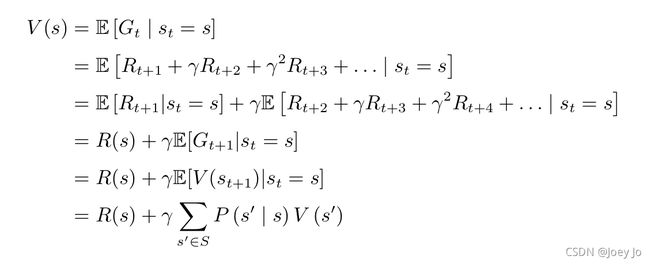强化学习过程笔记 （二） MDP 马尔可夫决策过程、贝尔曼等式详解

Markov Process & Markov chain 马尔可夫过程及马尔科夫链

如果一个状态是符合马尔可夫的，那就是说一个状态的下一状态只取决于它当前的状态，而跟它之前的状态都没有关系。

Markov Reward Process

马尔可夫过程加上一个奖励函数便构成了马尔可夫奖励过程

这里我们进一步阐述和温习一些概念及定义。

Horizon指一个回合的长度（每个回合的最大时间步数），它由有限个步数决定的

Return指把奖励折扣后所获得的收益，可以定义为奖励的逐步叠加：

正如我们上一篇博客所讲的一样。是折扣因子， 一般，我们可以观察到越靠后时间所取得的奖励前面的折扣就越多，的作用在于我们尽可能在短的时间里面去的尽可能多的奖励，时间越向后所获得的奖励就要乘上越多的小于一的，使得奖励变少。同时，的存在也可以避免闭环的产生；

当有了的定义后我们回过来看状态价值函数（state value function）

 一个状态对未来取得奖励的期望决定了它的价值，期望就是说从这个状态开始，你有可能取得多大的价值，这个值越大代表当前状态越有价值

Bellman equation的定义

我们可以从价值函数里面推导出Bellman Equation (贝尔曼等式)，如下

本式可以分为两部分：即刻收益 (Immediate reward)  
以及折扣未来收益 (Discounted sum of future reward) 

（准确来说是折扣因子 * 未来收益的期望，不清楚什么是期望的同学可以搜索全期望公式自行了解，本处不再赘述）

其中可以看做未来的所有状态

是指从当前状态转移到未来状态的概率。

代表的是未来某一个状态的价值。

那我们如何理解Bellman Equation？

以下是Bellman Equation的推导过程。

首先我们要明确一点：贝尔曼等式就是当前状态与未来状态的迭代关系，是对价值函数的一个拆分，将其拆为了立刻可以获得的收益和未来可能的收益。以下是贝尔曼等式的推导过程：

其中首先带入的定义，再将其分开，后半部分提取一个，

根据全期望等式可以推导出。

我们可以试着这样理解贝尔曼等式：

 时刻状态的价值 = 当前立刻可以获得的收益 + 折扣因子 * t+1状态的价值

而下一个状态的价值函数又可以同理理解为

t+1 时刻状态的价值 = t+1时刻可以立刻获得的收益+折扣因子 * t+2 状态的价值

通过如此往复迭代我们就可以将下一时刻价值 转化成未来所有状态价值。

故我们可以将贝尔曼等式理解为当前价值与“下一状态”价值之间的联系，所以前的就很好理解了。这里的“下一个状态”通过不断的迭代其实就是未来所有状态的收益。

贝尔曼等式是强化学习中的重中之重，一定要确保理解透彻。

对于小规模的MRP我们可以使用矩阵求逆的方法得到价值函数的解析解，不过这个方法用于大规模矩阵就很难实现了。

大规模的MRP求解价值函数可以使用动态规划算法(Dynamic Programming)，蒙特卡洛算法(Monte Carlo Algorithm)，时序差分学习(TD Learing)等。

动态规划就是不断迭代Bellman Equation，让状态的价值最后收敛，我们就得到了每个状态的价值。

蒙特卡洛算法即不断采样，举例来说就是让一只小船随波逐流，这样就会产生一个轨迹，进而得到一个奖励。我们可以算出折扣奖励，通过累加最终得到。通过大规模的这样进行采样后，对求得的所有求一个平均值，便可以得到状态的价值。

TD Learing 是动态规划和蒙特卡洛算法的一个结合。

Markov Decision Process马尔可夫决策过程

相较于MRP，MDP多了一个decision

已知一个MDP和一个policy ，我们可以将MRP转换成相应的MDP。

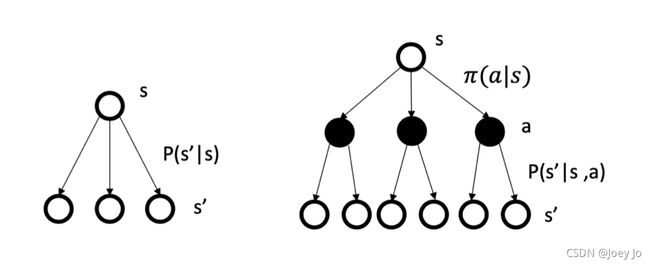
MP/MRP 与 MDP的比较

马尔可夫过程的转移是直接就决定。比如当前状态是s,那么直接通过这个转移概率决定了下一个状态是什么。

但对于MDP，它中间多了一层动作a。采取动作后到达什么状态也是一个概率分布（采取动作与到达状态并不是一对一的关系）

图示左边为MP/MRP，右边为MDP可以很直观地了解它们之间的差异。

 是在状态下采取动作的概率，是采取动作后，从状态转移到的概率。

MDP的Value Function

在MDP中，我们定义两个价值函数——状态-价值函数(statue-value function) 和动作-价值函数(action-value function)

状态-价值函数与MRP中的定义类似

注意这里的期望是针对policy的期望。

动作-价值函数即Q函数，定义为在某一状态采取某一动作，它有可能得到的这个return的一个期望

我们可以推导出Q函数的Bellman Equation： 

此处的推导过程与MRP的类似，不再重复

Bellman Expectation Equation

我们将状态-价值函数拆分为及时奖励(Immediate reward)和后续状态的折扣价值(Discounted sum of future reward)，得到Bellman Expectation Equation

有趣的一点是，贝尔曼期望等式其实就是另一种形式的贝尔曼等式，我们上述的对Bellman Equation理解方法便是根据Bellman Expectation Equation的定义来的。之所以称为贝尔曼期望等式，其实就是对贝尔曼等式求了了一个期望。可以进行如下转化

就是因为将贝尔曼等式中的根据期望和价值函数的定义转化为了

对于Q函数，我们也可以做类似的分解：

 

我们可以进行进一步的推导：

这个式子的意思是将在状态下所有可能采取的动作的q函数进行一个加和，便可以得到状态-价值函数。

再给出q函数的定义