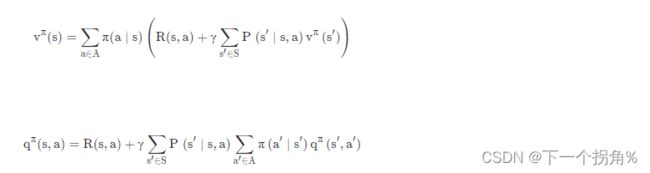强化学习-第二章-马尔可夫决策过程

蘑菇书 ：https://linklearner.com/datawhale-homepage/#/learn/detail/91

马尔克夫性质

        所有马尔可夫过程 都 满足 ：

       状态转移：一个状态的下一个状态只取决于它当前状态，而跟它当前状态之前的状态都没有关系。

       因此：从当前状态 s_t 转移到 s_t+1​ 这个下一状态，直接就等于它之前所有的状态（h_t :包含起始到当前t时刻 的所有状态）转移到 s_t+1​。

马尔可夫链（s、p）、马尔可夫价值(s,p,R)

        给定 状态转移P（条件概率）：从一个状态 可以到达 所有状态 的 概率，

       从一个 状态 开始 ，对马尔科夫链 进行  采样  ，可以得到 很多条 轨迹  episodes 。

【通过大量   采样  依据大数定律 ，从 某一个状态 开始 ，采样生成很多轨迹，计算得到的 奖励 ，取平均值，作为进入 这一状态  可以得到的奖励 。->蒙特卡洛算法】

     动态规划 【 反向传播（迭代），正向寻优 】

-》贝尔曼方程

-》后继状态值的估计来更新状态值的估计

-》迭代更新 上一状态，因此当 最后更新状态 和 上一状态  变化 并不大 时， 更新 可以停止-》输出 最新 的value 值 作为它当前状态 -》自举

 马尔可夫决策过程(s,p,R,decision(action))

   多了 一个决策 过程，所以下一状态  由当前状态s 和 选取 动作a（决策选择 什么动作 a） 共同影响 。在MRP 的条件上 加一个 a 。

预测 prediction ：

输入-- MDP 和 policy  π 

   这里MDP 表示 value function 的时候 是用 action -value function （某一个状态采取某一个动作，得到 return 的一个期望 ）：

   多了的策略 就是决策选择 何种动作 进入 下一状态s'，所以会得到一个概率

   这里 ，上面两式  相乘加和  ，就可以 去掉 a ，动作，这一个变量 因素，输出得到 value-function

  这里 计算 value-function 的 过程就是 策略评估（或者 预测） ，评估（预测）这个策略 会给我们得到多大的奖励 。

 【给定一个policy ，确定他的value function】

控制 control：

输入：MDP

输出：最佳价值函数(optimal value function) v∗ 和最佳策略(optimal policy) π∗。

【没有 policy 的前提下，我们要确定最优的 value function 以及对应的决策方案。  】

   因此要去 寻找最佳策略

寻找的过程分为 两种 ：策略迭代 、 值迭代 

策略迭代

策略评估+策略改进：

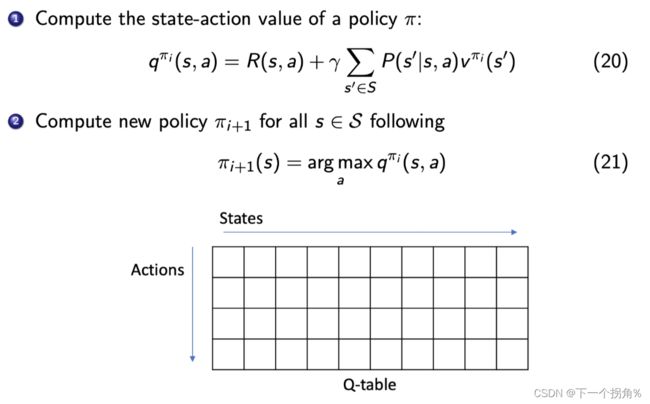
      （1）在初始化的时候，我们有一个初始化的 V 和 π ，给定当前的poilcy function （已经搜索过的）来估计v函数。  （2）根据 v 和 q 函数 的关系 ，推出 q函数 ，因为q函数 里面 包含这个 策略的变量  动作a ，然后 采用 贪心算法 ，把使得 q 最大 的 a 提取出来 得到 新的 策略 π' 

Bellman expectation equation 

 这里 Q 函数看成一个 Q-table。【是一个表格形式，所以Q-learning 表格型的 方法】

      对于某一个状态，每一列里面我们会取最大的那个值，最大值对应的那个 action 就是它现在应该采取的 action。

      所以 arg max 操作【贪心策略】就说在每个状态里面采取一个 action，这个 action 是能使这一列的 Q 最大化的那个动作。

 值迭代

    直接用 贝尔曼最优方程 去迭代 ，每一步都是最优的

只是在解决一个 planning 的问题，而不是强化学习的问题，因为我们知道环境如何变化。value function 做的工作类似于 value 的反向传播。