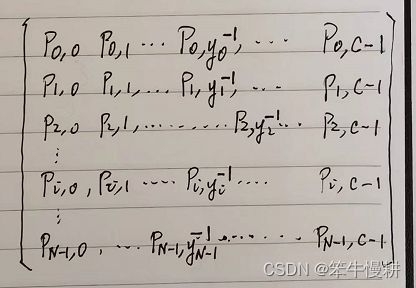cs231n-2022-assignment1#Q4：Two-Layer Neural Network(Part1)

目录

1. 前言

2. 数据加载

2. Affine layer: Forward

3. Affine layer: Backward

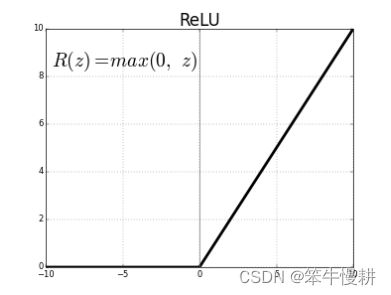
4. ReLU activation: Forward

5. ReLU activation: Backward

6. SVM loss and gradient 

7. Softmax loss and gradient

 8. Two-layer network¶

---

1. 前言

        本文是李飞飞cs231n-2022的第一次作业的第4个问题（Two-Layer Neural Network）。 前三个问题分别参见：

cs231n-2022-assignment1#Q1：kNN图像分类器实验

cs231n-2022-assignment1#Q2：训练一个支持向量机(SVM)

cs231n-2022-assignment1#Q3：Implementing a softmax classifier

        本次作业相关的课程内容参见：CS231n Convolutional Neural Networks for Visual Recognition

        建议有兴趣的伙伴读原文，过于精彩，不敢搬运。本文可以作为补充阅读材料，主要介绍作业完成过程所涉及一些要点以及关键代码解读。作业的原始starter code可以从Assignment 1 (cs231n.github.io)下载。本文仅涉及完成作业所需要修改的代码，修改的文件涉及以下几个文件：

• cs231n/data_utils.py
• cs231n/layer_utils.py
• cs231n/layers.py
• cs231n/classifiers/fc_net.py
• root/two_layer_net.ipynb
   

2. 数据加载

        和前几篇一样，改为用keras加载cifar10数据集。修改data_utils.py :: get_CIFAR10_data()中的一部分如下：

    # # Load the raw CIFAR-10 data
    # cifar10_dir = os.path.join(
    #     os.path.dirname(__file__), "datasets/cifar-10-batches-py"
    # )
    #X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
    (X_train, y_train), (X_test, y_test) = keras.datasets.cifar10.load_data()
    y_train = np.squeeze(y_train)
    y_test  = np.squeeze(y_test)
    X_train = X_train.astype('float')
    X_test  = X_test.astype('float')

        该函数中完成了

• （1）数据集加载；
• （2）训练、验证和测试集的分割；
• （3）均值归一化；
• （4）shape调整；

        最后将所有数据存放在一个dict中输出出来。

        需要注意的时，在“shape调整”中特意地将channel轴调整到第2维，即由{N,H,W,C}调整为{N,C,H,W}。两种表示方式在深度学习中都有，Tensorflow/Keras是采用前一种。

2. Affine layer: Forward

         cs231n/layers.py:: affine_forward()。

        本函数实现功能可以表达为：

        其中X表示数据集，第1个轴（第1个维度）为样本维。函数中首先将X中的每个样本由shape={C,H,W}变成一个1维的向量，其长度与w的长度是匹配的，然后再执行仿射变换。在numpy中用"@"表示矩阵乘法，用matmul()，或者dot()也可以。

out = np.reshape(x, (x.shape[0], -1)) @ w + b

3. Affine layer: Backward

        

        其中就是以下函数中的输入参数dout，其物理含义为（最终的损失函数对）该层输出张量Y的梯度。 

def affine_backward(dout, cache):
    """
    Computes the backward pass for an affine layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    dx, dw, db = None, None, None

    dx = np.reshape(dout @ w.T, x.shape)
    dw = np.reshape(x, (x.shape[0], -1)).T @ dout
    db = np.sum(dout,axis=0)

    return dx, dw, db

4. ReLU activation: Forward

        ReLU的公式是：

        ReLU还有两个常见的变体：

        Leaky ReLU：

        Exponential ReLU（ELU）：

def relu_forward(x):
    """
    Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """

    out = x.copy() # Note: "out = x" is NG!
    out[x<0] = 0

    cache = x
    return out, cache

5. ReLU activation: Backward

        显而易见的是，

        当x>0：ReLU函数的导数为1

        当x<=0：ReLU函数的导数为0

def relu_backward(dout, cache):
    """
    Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache


    dx = np.zeros(x.shape)
    dx[x>0] = 1
    dx = np.multiply(dx, dout)

    return dx

6. SVM loss and gradient 

        计算方式与Q2中的SVM loss及梯度计算基本相同，但是有一点点区别。

        在Q2中的SVM layer是包含仿射映射部分的，所以loss和梯度计算中是针对仿射映射输入数据X以及参数W的。而在本问题（一般来说在深度神经网络）中，将SVM 和仿射映射看作是分离的层。因此本问题中的SVM layer的输入已经是仿射映射的输出，即Q2中的scores。所以loss和gradient的计算相当于只是Q2中的对应计算的一部分（不需要考虑由仿射映射输出针对仿射映射输入以及W的梯度部分）。loss函数修改如下（注意与Q2中的SVM loss函数的不同）

                

                 

def svm_loss(x, y):
    """
    Computes the loss and gradient using for multiclass SVM classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss = 0.0
    dx = np.zeros_like(x)

    #############################################################################
    # TODO: Compute the softmax loss and its gradient using no explicit loops.  #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    num_train = x.shape[0]
    num_classes = x.shape[1]
    
    scores = x # shape: (N,C) = (num_train,num_classes)
    correct_class_scores = scores[np.arange(num_train),y]
    
    margins    = scores - np.expand_dims(correct_class_scores,axis=1) + 1 # Broadcasting

    margins[np.arange(num_train),y] = 0.0
    margins[margins<=0] = 0.0   

    loss      = np.sum(margins)/num_train # No need of nested nu.sum()   

    margins[margins>0]=1.0
    row_sum = np.sum(margins,axis=1)
    #margins[np.arange(num_train),y] = -row_sum
    for i in range(num_train):
        margins[i,y[i]] = -row_sum[i]
    dx = margins/num_train
    return loss, dx

         这个代码是在Q2的svm_loss_vectorized的代码经过删减而得。有兴趣的小伙伴可以对比两个代码看看它们的差异以加深理解。

7. Softmax loss and gradient

        计算方式与Q3中的Softmax loss及梯度计算基本相同，但是有一点点区别。

        在Q3中的Sofmax layer是包含仿射映射部分的，所以loss和梯度计算中是针对仿射映射输入数据X以及参数W的。而在本问题（一般来说在深度神经网络）中，将softmax和仿射映射看作是分离的层。因此本问题中的softmax layer的输入已经是仿射映射的输出，即Q3中的scores。所以loss和gradient的计算相当于只是Q3中的对应计算的一部分（不需要考虑由仿射映射输出针对仿射映射输入以及W的梯度部分）。

def softmax_loss(x, y):
    """
    Computes the loss and gradient for softmax classification.

    Inputs:
    - x: Input data, of shape (N, C) where x[i, j] is the score for the jth
      class for the ith input.
    - y: Vector of labels, of shape (N,) where y[i] is the label for x[i] and
      0 <= y[i] < C

    Returns a tuple of:
    - loss: Scalar giving the loss
    - dx: Gradient of the loss with respect to x
    """
    loss  = 0
    dx    = np.zeros_like(x)

    ###########################################################################
    # TODO: Copy over your solution from A1.
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    num_train = x.shape[0]
    scores = x
    scores = scores - np.max(scores,axis=1,keepdims=True)
    exp_scores = np.exp(scores)
    probs  = exp_scores / np.sum(exp_scores,axis=1,keepdims=True)
    loss   = -np.sum(np.log(probs[range(num_train),y]))
    
    dx     = probs
    dx[range(num_train),y] -= 1
    
    loss   = loss / num_train #+ 0.5 * reg * np.sum(W*W)
    dx     = dx / num_train #+ reg * W    

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return loss, dx

        如上所示，代码的主体部分与Q3的ssoftmax_loss_vectorized拷贝而来，但是删除了仿射映射部分（将输入x直接赋值给scores）。

        所求梯度的表示如下（具体推到可以参考Q3），其中

       最后，正则化部分也不需要了（正则化是针对W的）。 

        

 8. Two-layer network¶

        在class TwoLayerNet中包含两个方法，一个是初始化方法；另一个是loss()。需要实现一个两层神经网络，其结构为：affine - relu - affine - softmax.

        第一层是affine 层（即通常所说的全连接层）后跟relu激励层（通常合称为一层，即带relu激励的全连接层）；第二层为带softmax激励函数的全连接层。

        loss()可以工作在训练模式或者测试模式，在测试模式只返回scores，即softmax的输入数据；在训练模式则返回总体损失值及损失函数对各参数的梯度。

        注意，在之前的几个问题中，都是把bias合并到到W中去。但是，在深度神经网络中则通常把b和W分开来处理。其中一个差别是，通常来说正则化处理不需要考虑bias。当然，之所以将bias和Weight分开来处理可能还有别的原因，或者仅仅是一种约定俗成的convention？

        __init__的代码如下所示：

        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        self.params['W1'] = np.random.normal(loc=0.0, scale=weight_scale, size=(input_dim,hidden_dim))
        self.params['b1'] = np.zeros((hidden_dim,))
        self.params['W2'] = np.random.normal(loc=0.0, scale=weight_scale, size=(hidden_dim,num_classes))
        self.params['b2'] = np.zeros((num_classes,))

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        loss()的代码如下所示。基本上就是基于前面准备好的affine/relu_forward/backward跟搭积木似的堆砌起来。不过，如果没有这个starter code，以及这样循序渐进的作业安排，真要写一个这样的模型from sratch，还是有相当难度的，包括深度学习算法以及编程技能两个方面。有starter code难度就降低了差不多一个量级了。

        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        W1 = self.params['W1']
        b1 = self.params['b1']
        W2 = self.params['W2']
        b2 = self.params['b2']

        affine1_out, affine1_cache = affine_forward(X,W1,b1)
        relu_out, relu_cache = relu_forward(affine1_out)
        affine2_out, affine2_cache = affine_forward(relu_out,W2,b2)
        
        scores = affine2_out

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        # If y is None then we are in test mode so just return scores
        if y is None:
            return scores

        loss, grads = 0, {}
        ############################################################################
        # TODO: Implement the backward pass for the two-layer net. Store the loss  #
        # in the loss variable and gradients in the grads dictionary. Compute data #
        # loss using softmax, and make sure that grads[k] holds the gradients for  #
        # self.params[k]. Don't forget to add L2 regularization!                   #
        #                                                                          #
        # NOTE: To ensure that your implementation matches ours and you pass the   #
        # automated tests, make sure that your L2 regularization includes a factor #
        # of 0.5 to simplify the expression for the gradient.                      #
        ############################################################################
        # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        loss, d_affine2_out = softmax_loss(scores, y)
        loss += 0.5 * self.reg * ( np.sum(np.square(W1)) + np.sum(np.square(W2)) ) #+ np.sum(np.square(b1)) + np.sum(np.square(b2)) ) # No need of L2 regularization for bias       
        d_relu_out,dw2,db2  = affine_backward(d_affine2_out, affine2_cache)
        d_affine1_out       = relu_backward(d_relu_out, relu_cache)
        d_X,dw1,db1         = affine_backward(d_affine1_out, affine1_cache)
        
        # Add regularization part for dw2 and dw1
        dw1 += self.reg * W1
        dw2 += self.reg * W2
        
        grads['W1'] = dw1
        grads['b1'] = db1
        grads['W2'] = dw2
        grads['b2'] = db2

        # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
        ############################################################################
        #                             END OF YOUR CODE                             #
        ############################################################################

        return loss, grads

        这一个作业容量也太大了。。。剩下部分留待下次。