GAMES202-Environment Mapping概括总结

截图均来自于闫令琪老师的GMAES202-Environment Mapping，本文在于对课程内容进行总结并加上自己的理解以及对一些数学公式的推导，来方便大家理解课程，如有谬误请各位指正

1.Distance functions

如下图为字母A的距离场（SDF-Signed Distance Function），一般定义成有向的距离场，其形状类似于等高线，表示空间中某一点到物体表面最小的距离为多少





那么我们使用SDF来干什么呢
如下图所示，上面的第三个正方形为A和B线性插值得到的结果，如果黑色为0白色为1，线性插值得到的灰色区域则为0.5
而这并不是我们想要的结果





于是我们使用SDF方法设黑色为<0的值-1，白色为>0的值1，轮廓线为0，将A和B的轮廓线进行插值后得到一个居中的轮廓线0，然后将<0和>0的地方进行填充则得到了我们想要的插值结果

同理SDF在几何过渡方面也有很广泛的应用，如下图所示

2. The Usages of Distance Fields

Usage 1

Ray Marching，即用光线追踪追踪距离场，看能打到哪个物体表面

如上图所示，从某一点做SDF，会得到一个圆，因为SDF的定义表示某点到某物体的最近距离，那么在这个圆内不会与任何物体相交（安全距离），然后沿着某一方向与圆交一点，在这个点上继续做SDF，如此反复，直到与某个物体的距离足够近时停止，这样我们就可以得到每个物体最小的SDF，之后会方便计算

Usage 2

用来生成软阴影

如上图所示从一个shading point在某个方向打出一根光线，在光线的中间某一点使用SDF会得到一个安全距离，安全距离越小，我们再定义一个安全角度用来表示光线离物体的远近，安全角度越小，那么阴影就越“硬”，如果这个这跟光线与物体相较，则表示完全被遮挡，阴影就更黑

由上图，在光线的每一个点都能得到一个安全角度，其中最小的便是最能反映这条光线的安全角度，那我我们就能得到在这个角度下的阴影软硬情况
我们可以通过黄色圆半径除以OP3的长度，在解一个arcsin即可得到这个角度
但其实计算反三角函数是比较消耗资源的
大佬们又双叕发现了更加简单的方法
min{$\frac{k\cdot R}{OP},1.0$}
即用半径R比上OP的长度得到一个数，再将这个数与1做比较，确保结果是以一个小于等于1的数（Visibility）
通过乘k来控制到达1.0的快慢程度，如果k很大，那么很小的安全角度都会算作硬阴影
由此可得，我们可以通过k来控制阴影的软硬程度

SDF的优点：
快速，高质量

SDF的缺点：
需要预计算（存空间的大量SDF信息）
需要很大的存储（三维）

补充：现在SDF被大量应用到文字方面，用来对放大的文字的锯齿进行插值，使其有更平滑的过度

3. Environmen Lighting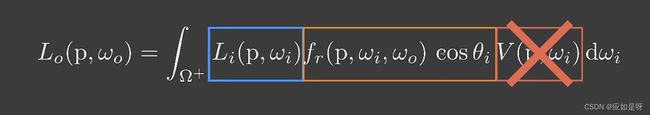

上图为渲染方程，我们目前不用考虑visibility项
在通常情况下我们可以使用蒙特卡洛积分通过采样来解渲染方程，但同时也会消耗大量资源（目前的一些GPU可以胜任这些工作，但我们暂且不考虑）
那么我们如何能避免大量采样呢

我们不妨来看看不同情况下BRDF的特性
glossy情况下（左图），覆盖的范围很小
diffuse情况下（右图），覆盖区域较大且比较平滑
这就让我们想到了一个近似公式，此公式使用的情况是g(x)的值比较小或者比较平滑，恰好满足了BRDF的条件

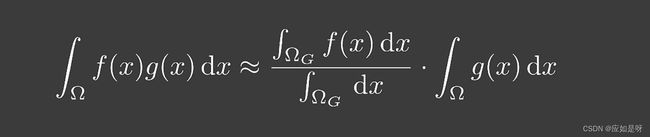
4. Split Sum

那么我们把BRDF的光照项拆出来

黄色的框里是先对光照项的积分再对其进行归一化，物理意义就是对他进行模糊处理（即滤波操作），如下图

使用不同的滤波的核对其滤波会产生不同程度的模糊效果，核的大小跟BRDF对应的区域有关，BRDF的区域越大核越大，得到的图就越模糊

可以储存不同大小的滤波核来方便查询，例如存入半价大小为1，2，4，8的图

那如果我需要一张半价为5的图呢，我们可以通过想mipmap一样由4核8线性插值得到

那我们得到这些滤波的图后是用来干什么呢？
不妨先看下图

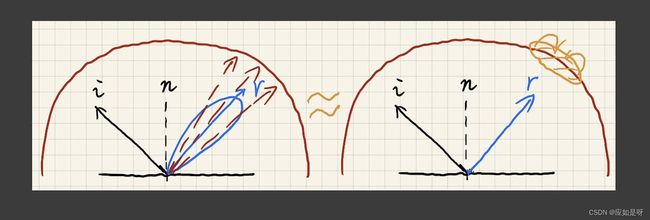
左图表示从某个方向看一个shading point，其对应的BRDF是某种lobe（反射波瓣），在通常情况下我们可以通过采样BRDF的lobe中的值并进行加权平均，然后得到shading point的值
那么刚刚我们在做的事不就是把environment lighting做一个滤波操作吗，右图表达的就是在镜面方向查一个已经预计算过的值，而这个值恰好就是对周围值的加权平均，所以我们可以将这两个方法进行约等

那现在我们就通过了预计算的方法解决了渲染方程中的光照项
还剩下BRDF项，即下图红色框内的积分

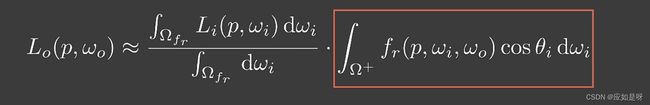
这是一个有五个未知数的积分，那么如果预计算的话我们需要打一个五维的表格（不要管为什么是五维，超过三维一律不考虑），那么存储量就会直接爆炸

那么让我们回忆一下Microfacet BRDF是如何求解的

红色为菲涅尔项，表示如果垂直看向物体表面有多少能量被反射，以及如果不垂直怎么反射，其直接作用于颜色的显示
蓝色项表示的是微表面的法线分布，如果法线比较分散，则表明比较粗糙发生漫反射，如果法线方向比较集中，则表明表明光滑发生镜面反射
中间项目前不用考虑

我们可以用Schlick‘s approximation来近似描述菲涅尔项
这个方法主要可以把菲涅尔项看作一个关于初始反射率（基础颜色）$R_0$和$\theta$的指数函数
那么微表面的法线分布可以使用Beckmann分布进行近似表示
我们可以通过下图看对这两项近似的结果比较，基本符合

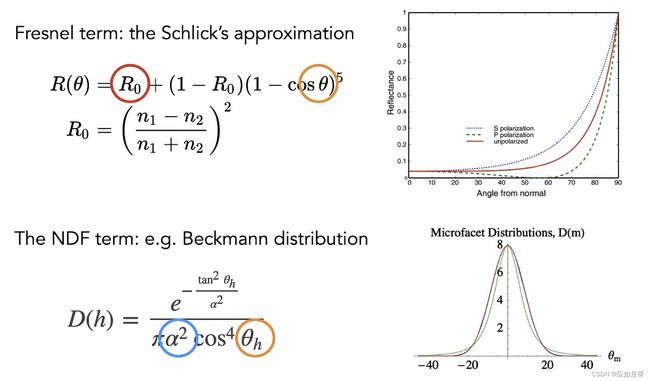
图上画的三种颜色的圈代表三个变量，那么这样我们就把BRDF由五维降到了三维

那这样就结束了吗？

并没有

大佬们又双叕发现了降成二维的方法

这里我给大家贴心的推导一下如何降维

我们可以把R0作为一个常数提出去，这样就消除了基础反射率低影响把BRDF项变成了关于$\theta$和$Routhness$的一个函数，我们只要打一个二维的表格即可解决问题

将上图储存为一张纹理送到shader中使用即可

到现在为止我们又一次地解决了采样的问题，把渲染公式的两项都通过预计算➕存储的方式解决了，顺便提一句，预计算在实时渲染尤其是游戏中使用十分广泛，可以通过预计算来显示更精美的画面以及更高的帧数