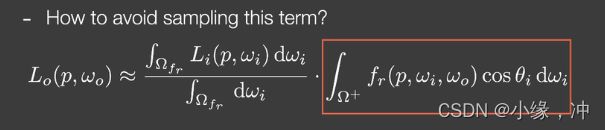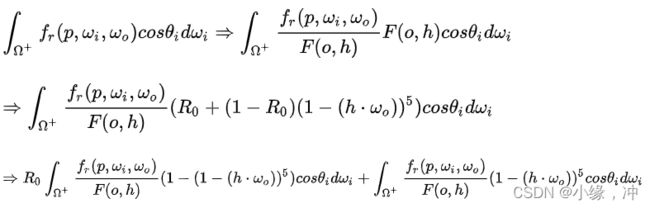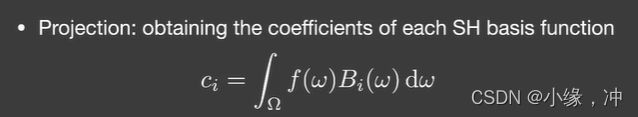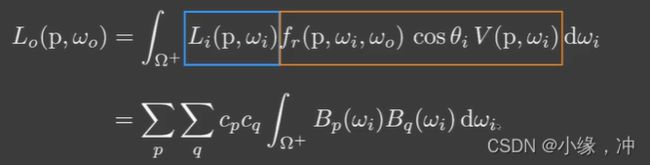GAMES202 笔记 -Real-Time Environment Mapping
目录
一、环境光照-无阴影
二、Prefiltering
三、BRDF项采样
四、环境光照-阴影
五、Basis Functions
六、Spherical Harmonics(球谐函数)
七、PRT
八、Light transport
九、小波
一、环境光照-无阴影
环境贴图就是在场景中任意一点往四周看去可看到的光照,将其记录在一张图上这就是环境光照,或者也可以叫做IBL(image-based lighing)我们用spherical map和cube map来存储环境光照.
使用Spherical Map记录环境光同时存在一些问题,注意上图的上下边界,你会发现出现了扭曲的情况。这是因为球面展开成为平面的时候,平面无法均匀的描述球面上的所有信息,纬度越高的地方,在球面上占据的区域越小,展开后扭曲越严重。
使用环境光计算shading的操作叫做IBL(Image based lighting)。如果已知环境光照,此时放置一个物体在场景中间,在不考虑遮挡时我们该如何去得到任何一物体上任何一shading part的shading值:
不考虑遮挡,所以舍去visibility项,那么式中的lighting项就变成了环境光的lighting,而不是到达着色点的lighting.通用的解法是使用蒙特卡洛积分去解,但是蒙特卡洛需要大量的样本才能让得出的结果足够接近,如果我们对每个shading point都做一遍蒙特卡洛,那样的话将会花费很多时间在采样上。
避免采样:由于我们不考虑visibility项,那么rendering equation就只是brdf项和lighting项相乘再积分。brdf又分为两种情况。
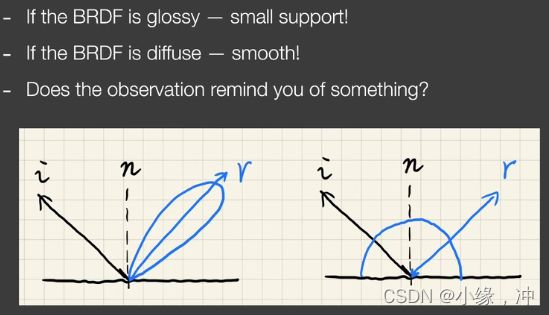
对于渲染方程中的BRDF项来说,如果是glossy材质的BRDF,如上图左所示(图中i方向是相机方向,r方向是光源方向),则其lobe很小,即积分域很小;如果是diffuse材质的BRDF,如上图右所示,虽然lobe很大,但足够smooth。
由公式拆分:
把light项拆分出来,然后将brdf范围内的lighting积分起来并进行normalize归一化,其实就是将IBL这张图给模糊了。
二、Prefiltering
模糊就是在任何一点上取周围一片范围求出范围内的平均值并将平均值写回这个点上。一般来说,会选择不同尺寸的滤波核,对环境光贴图进行不同层次的滤波,当使用时,可以根据BRDF的lobe的实际大小在对应层次的滤波结果上查询,BRDF的区域越大,最后取得的图也就越模糊。-参考MIPMAP。
左图为brdf求shading point值时,我们要以一定立体角的范围内进行采样再加权平均从而求出shading pointd的值.右图为我们从镜面反射方向望去在pre-filtering的图上进行查询,由于图上任何一点都是周围范围内的加权平均值,即先采样后平均≈先平均后采样。解决了渲染方程近似拆分的前半部分,也就是lighting项的采样问题。
三、BRDF项采样
我们仍然可以用预计算来解决后半部分积分采样的问题,但是预计算的话我们需要将参数的所有可能性均考虑进去,但是比较多。因此我们需要想办法降低维度,也就是减少参数量从而实现预计算。
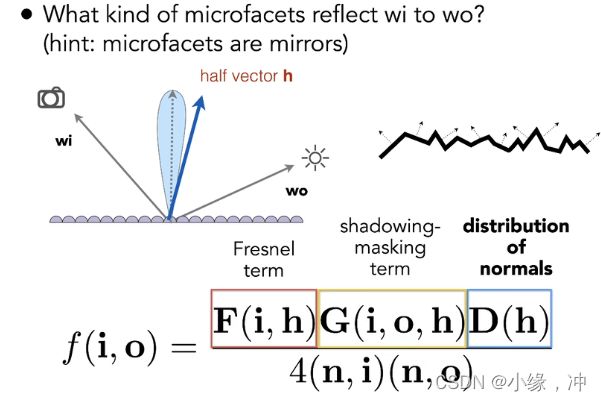
我们使用的是Microfacet BRDF:
- F是菲涅尔项,主要参数有三通道的初始反射率R0 ,以及观察方向 W0
- G是几何项/阴影项,主要表示微表面之间的遮挡关系,主要参数有法线n,观察方向 W0
- D是法线分布函数(NDF),主要参数有观察方向 W0,粗糙度等
暂时不考虑阴影,此处需要关注的是Fresnel term和distribution of normals
Frenel term可以近似成一个基础反射率R0和入射角度的指数函数
法线发布函数(NDF)是一个一维的分布,其中有两个变量,一个变量定义是diffuse还是gloosy,另一个 是half vector和法线中间的夹角,可以近似成入射角度相关的数,这样就变成了3维的预计算。
我们对原BRDF项做下列变形:
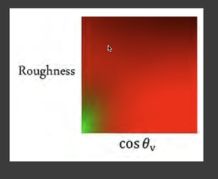
基础反射R0被拆出积分式,需要预计算的两个量就只有roughness ![]() 和角度
和角度 ![]() ,可以将预计算结果绘制成一张纹理,在使用时进行查询即可。预计算是固定。
,可以将预计算结果绘制成一张纹理,在使用时进行查询即可。预计算是固定。
四、环境光照-阴影
在有了环境光照情况下如何去得到物体被环境光照射下生成的阴影:
- many light问题:我们把环境光理解为很多个小的光源,这种情况下去生成阴影的话,需要在每个小光源下生成shadow map,因此会生成线性于光源数量的shadow map。
- 对光源进行采样并不困难,甚至可以进行重要性采样类似的操作,但是每个着色点的visibility项可能是完全不同的,也就是我们很难知道在某个点的某个采样方向上,visibility项是什么。也就是我们只能对visibility项进行盲目的采样,导致结果收敛的很慢。
在工业界中,我们通常以环境光中最亮的那个作为主要光源,也就是太阳,只生成太阳为光源的shadow
与生成环境光下阴影相关的研究:
- Imperfect shadow maps:是生成全局光照下阴影的一个解决方案
- Light cuts:是离线渲染领域中一系列有关many-light问题的相关研究
- RTRT(real-time ray tracing):可能是环境光下生成阴影的一个终极解决方案
- Precomputed radiance transfer(prt):可以准确的得到环境光下阴影的结果
五、Basis Functions
傅里叶级数展开:任何一个函数可以写成常数和一系列基函数(不同频率sin和cos项)的线性组合,基函数数量越多越接近于原函数的形状。
频率:在空间上图像信号数值的变化是否剧烈,如头发区域属于高频,因为是一根一根的,衣服,背景等变化不剧烈的属于低频,可以用频谱表示。
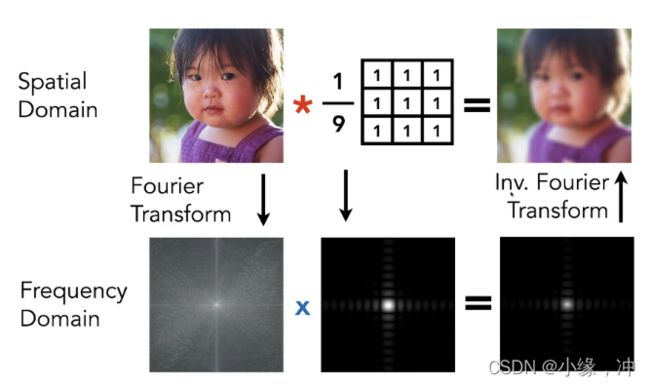
卷积:其实就是一个模糊操作,在图上取任意一点,取点的周围一定区域内的像素值进行加权平均并将结果写回这个点。在spitial域上做卷积也就等于在函数上做一个卷积,就等于在频域上做一个 原图频谱 和 卷积核频谱 的乘积操作。
对于任意的product integral(两个函数先乘积在积分),我们将其认为是做了一个卷积操作,理解为spatial域上的两个信号f(x)和g(x)进行一个卷积,等于在频域上让两个信号相乘,如果两个信号有一个信号是低频的,那么频域上相乘后得到的结果也是低频的,最终相乘在积分的结果也是低频的。
把一个函数可以描绘成其他函数的线性组合,如f(x)可以描绘成一系列的Bi函数乘以各自对应的系数最终再相加在一起,这一系列的函数Bi就是基函数。
六、Spherical Harmonics(球谐函数)
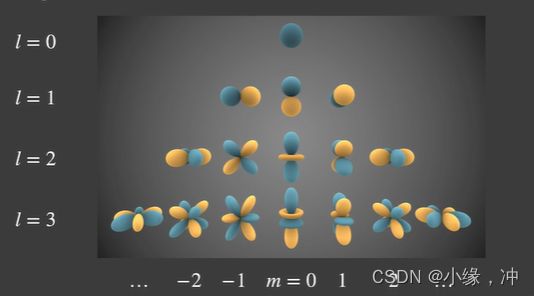
SH是一系列基函数,系列中的每个函数都是2维函数,并且每个二维函数都是定义在球面上的。
SH的可视化:图中的颜色表示的是值的大小,越偏白的蓝色地方值越大,越黑的地方值越小。而黄色中则表示偏白的地方表示其绝对值大,偏黑的地方表示绝对值小。也就是蓝色表示正,黄色表示负。
其中,l表示的是阶数,通常第l阶有2l+1个基函数,前n阶有个n*n基函数,m表示的是在某一个频率下基函数的序号,分别从-l一直到l。
投影/重建:确定基函数前面的系数,知道基函数对应的系数,就能用系数和基函数恢复原来的函数。
性质:
正交性: 能够较简单地投影/重建、simple rotation。
“积分之后的频率取决于积分前最低的频率”,当diffuse BRDF使用低频信息即可恢复内容时,也就意味着无论光照项是多么复杂,其本应该用多高频的基函数去表示,但我们希望得到的是其与BRDF之积的积分,所以可以使用比较低频的基函数去描述灯光。
七、PRT
在实施渲染中,我们把rendering equation写成由三部分组成的积分:
光照项,visibility项和brdf项,这三项都可以描绘成球面函数,这里用的是cube map描述法,那么最简单的解这个方程的方法就是每个像素挨个去乘对于每个shading point来说,计算shading需要计算6*64*64次。这个开销是十分大的。
把rendering equation分为两部分,lighting 和 light transport.
假设在渲染时场景中只有lighting项会发生变化,由于lighting是一个球面函数,因此可以用基函数来表示,在预计算阶段计算出lighting。而light transport(visibility和brdf)是不变的,因此相当于对任一shading point来说,light transport项固定的,可以认为是shading point自己的性质,light transport总体来说还是一个球面函数,因此也可以写成基函数形式,是可以预计算出的。
Diffuse:在diffuse情况下,brdf几乎是一个常数,因此我们把brdf提到外面,lighting项可以写成基函数,因此把其代入积分中,对于任何一个积分来说,在Bi的限制下,li此对积分来说是常数。Bi是基函数,v和cos项就是light transport。
- light transport做了预计算,因此visibility当了常量,因此场景不能动,因此只能对静止物体进行计算.
- 对于预计算的光源我们把它投影到sh上,如果光源发生了旋转,就相当于换了个光源。-旋转不变性:任何一个SH基函数旋转后都可以被同阶的SH基函数线性组合表示出来
1.brdf是diffuse相当于是一个常数,因此可以提到外面.
2.由于环境光照是一个球面函数,因此可以用sh基函数的线性组合表示,把其代入,由于li相对于积分是一个常数,可以提出
3.剩下的light transport项也可以看作一个球面函数,现如今积分里剩基函数和球面函数,相当于函数投影到基函数求系数,因此变为了一个系数
渲染方程中的lighting和light transport,都用sh基函数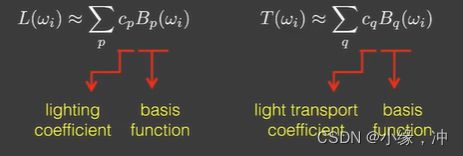
原式:然后把两个都展开成求和,然后把求和符号拆出去,然后就变成了一个双重求和的结果
- 对应的两个系数
- 积分值(积分与实际场景无关,是两个基函数的product integral)
glossy:Diffuse和glossy的区别在于,diffuse的brdf是一个常数,而glossy的brdf是一个4维的brdf(2维的输入方向,2维的输出方向).glossy物体有一个很重要的性质,它是和视点有关的.即使light transport即使投影到了i方向上的基函数,所得到的仍然是一个关于O的函数而不是系数.
我们将4D的函数投影在2D上之后,虽然得到的是一个关于O的函数,但是现在这个函数也只是关于O了,因此我们在O的方向上将其投影到SH基函数上.
light transport上就不再认为得到的是向量了,而是一个矩阵,也就是对于任意一个O都会得到一串VECTOR,最后把所有不同O得到的VECTOR摆在一起,自然而然就形成了一个矩阵,会产生巨大的存储。
基函数个数:9个(三阶)-diffuse足够16(四阶)25个(五阶)
- Diffuse 物体:每个点需要两个长度为16的向量点乘
- Glossy 物体:每个点需要16阶向量与16*16矩阵乘
八、Light transport
区分材质区分为三种:
- Diffuse
- Specular镜面反射
- Glossy 介于两者之间
路径:
- LE:Light直接到eye;
- LGE:light打到Glossy物体然后到eye。
- LGGE:多bounce一次,就是light先打到壶嘴,在bounce到壶身,最后到eye。(L->glossy->glossy->eye)
- L(D|G)*E:Light从光源出发,打到一个物体,可能是diffuse也可能是glossy,*表示bounce次数,最后到达EYE.
- LS(D|G)*E:打到Specular面上,然后聚焦到Diffuse物体上,最后被眼睛看到。也就是caustics.
将Basis看成奇怪光照,把light transport的预计算看作是一个在一些奇怪lighting下做的渲染过程.
把light和light transport,不管light transport有多复杂,bounce了多少次,只要进行了预计算,可以把任意复杂的light transport给预计算出来渲染时实际跑的时候是很简单的。
缺点:
- 由于球谐函数的性质,该方法比较适合使用于低频的情况
- 当改变场景或者材质时需要重新预计算light transport,此外预计算的数据比较大
基函数除了可以使用球谐函数外,还有很多选择,比如Wavelet、Zonal Harmonics、Spherical Gaussian、Piecewise Constant等。
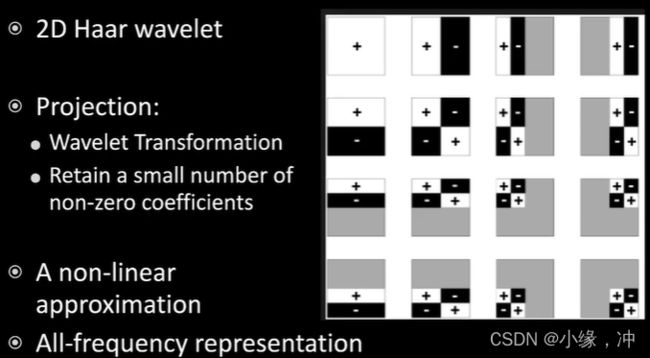
九、小波
由于小波是平面上的函数,为了防止变换后在球面上出现缝隙,所以采用了Cubemap来作为环境光而不是sphereical map。
高频信息留在图的左下,右上和右下三部分,而把剩余的低频信息放在左上角,左上角的信息可以继续进行小波变换,我们会发现高频的东西很少,对于绝大部分来说是0,不断地进行小波变换可以得到一个很不错结果。
小波不支持旋转。
jpeg-离散余弦变换