GAMES202-高质量实时渲染-闫令琪——Lecture 3:Real-Time Shadows 1 学习笔记
Lecture 3:Real-Time Shadows 1
-
Recap: shadow mapping
[slides courtesy of Prof. Ravi Ramamoorthi]Issues from shadow mapping and solutions
-
The math behind shadow mapping
-
Percentage closer soft shadows
一、Shadow Mapping
-
A 2-Pass Algorithm
–The light pass generates the SM
–The camera pass uses the SM (recall last lecture)
shadow mapping是一个两趟的算法(渲染场景两遍),第一遍从光源看向场景,输出距离光源最近的最浅深度shadow map,第二遍从相机位置看向场景,配合刚刚的生成的最浅深度图shadow map,渲染出结果。
-
An image-space algorithm
–Pro: no knowledge of scene’s geometry is required
–Con: causing self occlusion and aliasing issues
shadow mapping是一个完全在图像空间中的算法,好处是一旦shadow map已经生成,那么其就可以作为场景中的一个几何表示,为了得到最后的阴影,只需要shadow map即可,而不需要场景中的几何。
但是其会出现自遮挡和走样现象。
1、A 2-Pass Algorithm
Pass 1: Render from Light
Output a “depth texture” from the light source
第一趟从光源看向场景并渲染得到shadow map
Pass 2: Render from Eye
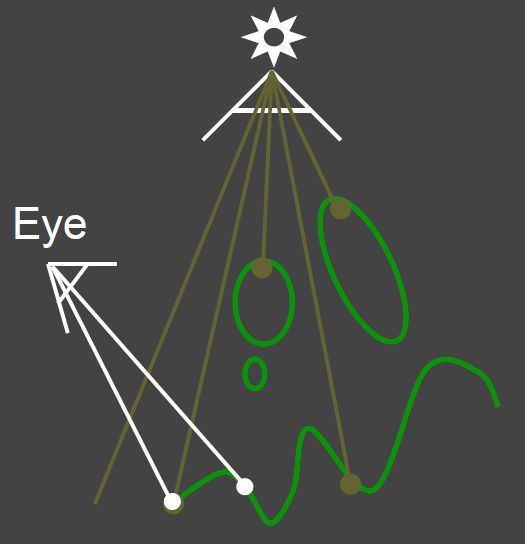
Render a standard image from the eye
第二趟从摄像机看向场景,并将看到的点再次连向光源
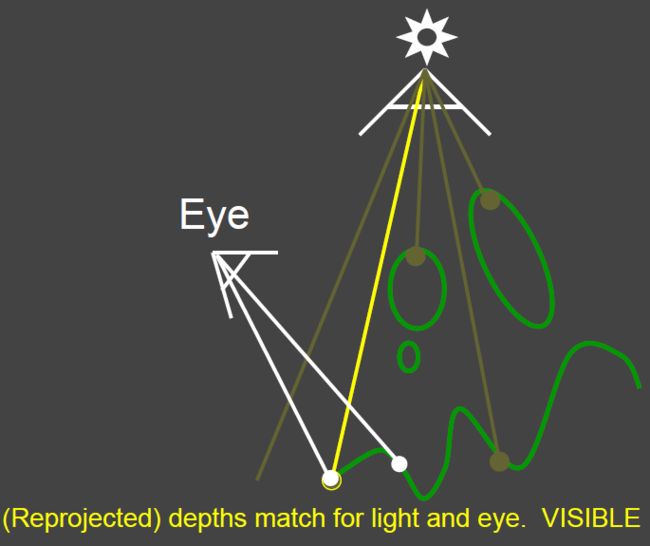
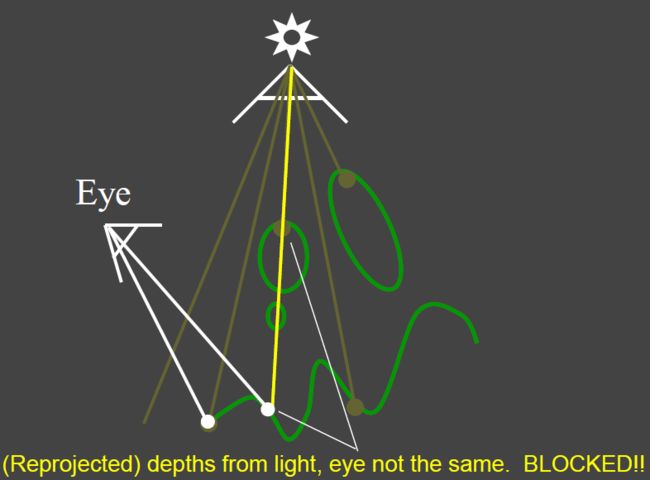
Pass 2: Project to light for shadows
Project visible points in eye view back to light source
如果看到的场景中的点到光源的距离与第一步中shadow map记录的深度值相等,则说明该点可见,如果不等,则说明该点被遮挡
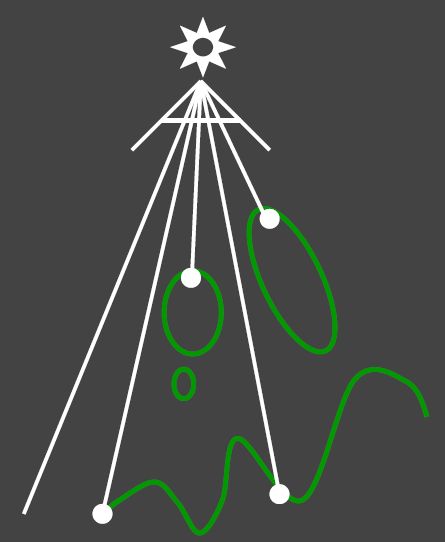
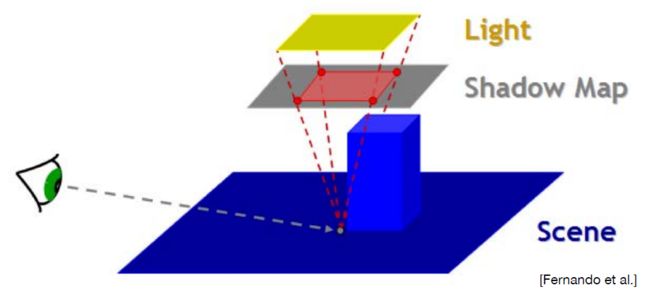
2、Visualizing Shadow Mapping
①、The depth buffer from the light’s point-of-view
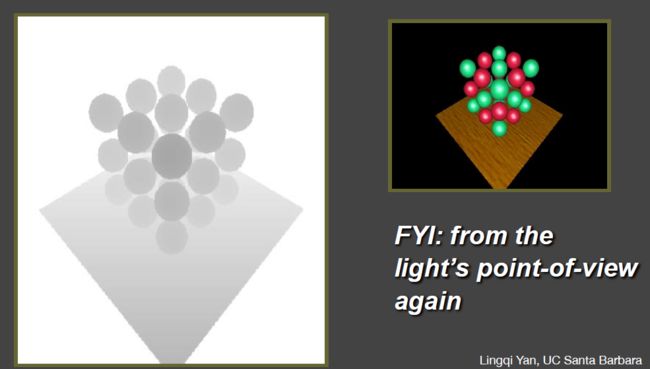
②、Projecting the depth map onto the eye’s view
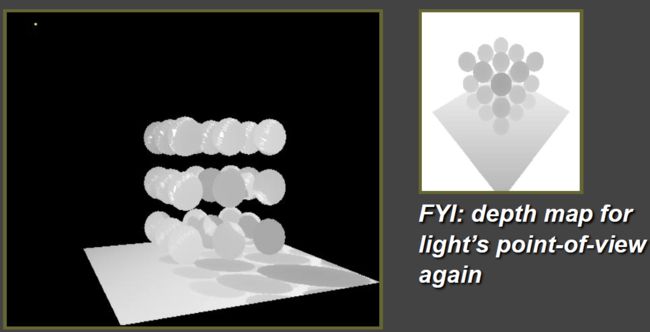
Scene with shadows

3、Issues in Shadow Mapping
(1)、Self occlusion

使用shadow map会产生自遮挡的问题,其产生的原因如下:
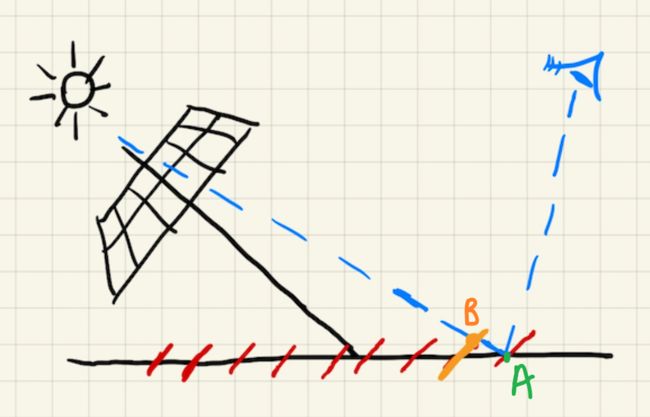
提前需要说明的是:在一个像素内部其深度是一个常数,所以在第一趟渲染shadow map时,从光源沿某一个像素的方向看向一个场景,看到的一个位置是覆盖该位置的一个像素所代表的深度,也就相当于这个场景在一个像素所覆盖的区域内都是一个常数深度,即shadow map将这样一个场景离散成了一系列小片拼成的场景(如上图红色),由于这个深度是从光源看向场景得到的,所以这些红色的小片与光源方向垂直。
对于上图这样一个平面场景来讲,在第一趟渲染中,从光源沿A点方向看向这个场景中的平面,理应能看到点A,但是由于shadow map将这样一个平面的场景离散成了一系列小片形成的场景,而被橙色的小片所遮挡,则shadow map上记录的是到点B的深度;
那么在第二趟从摄像机看向场景的渲染中,对于同一个点A却可以看到,再将A点连回光源处得到A点深度,但是在第一趟渲染shadow map时,这个方向上却被记录了光源到B点的深度,两趟的深度结果就不一致,导致点A处被认为是被遮挡的状态,导致了自遮挡问题的发生。
根据以上理论,在光源垂直于场景平面照射的时候,问题是最小的,而平行于场景平面照射,问题是最大的。
(2)、Adding a (variable) bias to reduce self occlusion
--But introducing detached shadow issue
我们可以让两次渲染得到的深度值在比较的时候有一个宽容度,差别在某个范围内则认为是相等。由于光源垂直于平面的时候问题最小,那么这时候宽容度可以比较低,而光源平行于场景的时候问题最大,这时候宽容度可以比较高,通过光源与平面的夹角去动态地调整这个宽容度。

但是这样得到的结果依然出现了问题。由于鞋跟处宽容度还是太大,而丢失了原本该有的遮挡。
(3)、Second-depth shadow mapping
--Using the midpoint between first and second depths in SM
--Unfortunately, requires objects to be watertight
--And the overhead may not worth it
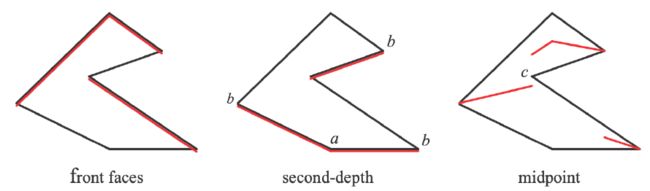
在这种方法里,在第一趟生成shadow map时,我们不仅存最小深度,还存次小深度。假设光从上往下照(如上图),那么最小深度就如左图所示,次小深度如中图所示。用最小深度和次小深度的中间深度作为shadow map来和第二趟的深度值比较。
但是其问题是任何模型都要有正反面,就算是一张纸都要做成一个很薄的box。
而且实现保留最小和次小深度本身也不容易,假设有这样一个可以计算的算法,则其输入是一系列无序的数,而始终要保持最小和次小,最小的很好比较,每次跟输入的值比较即可,但是涉及到最小和次小同时比较就要比较很多次。(虽然时间复杂度还是O(n),但是RTR does not trust in COMPLEXITY,实时渲染不相信复杂度,只相信绝对的速度)
(4)、Aliasing

由于shadow map上每个像素都可以理解成一个小片,投影出来的阴影图还会涉及到分辨率等问题,所以会出现锯齿。
二、The math behind shadow mapping
1、Inequalities in Calculus
There are a lot of useful inequalities in calculus

2、Approximation in RTR
- But in RTR, we care more about “approximately equal”
- An important approximation throughout RTR
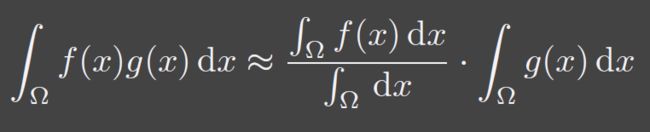
在实时渲染中我们更关心近似相等,在一系列条件下让不等变成约等。
3、In Shadow Mapping
- Recall: the rendering equation with explicit visibility

- Approximated as
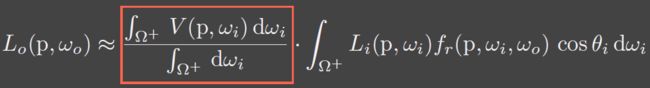
用刚刚的公式可以将渲染方程中的V拿出来做归一化。
这时左边是visibility部分,右边是shading部分,并且两者相乘,这正是shadow map的思路
When is it accurate?
--Small support
(point / directional lighting)
当积分限很小的时候,即小成一个很小很小的点(△),这个式子是准的,也就是当光源是点光源和方向光源时,这个式子没有问题。
--Smooth integrand
(diffuse bsdf / constant radiance area lighting)
当光照L不变,对应一个面光源(积分限是光源所对应的立体角上),面光源内部的radiance都不变,这里我们就可以认为L是完全smooth的,对于shading point,如果BRDF是diffuse的时候是smooth的。
因此当一个光源是面光源且shading point是diffuse时,这时我们也认为得到的结果是准确的。
三、Percentage closer soft shadows
From Hard Shadows to Soft Shadows
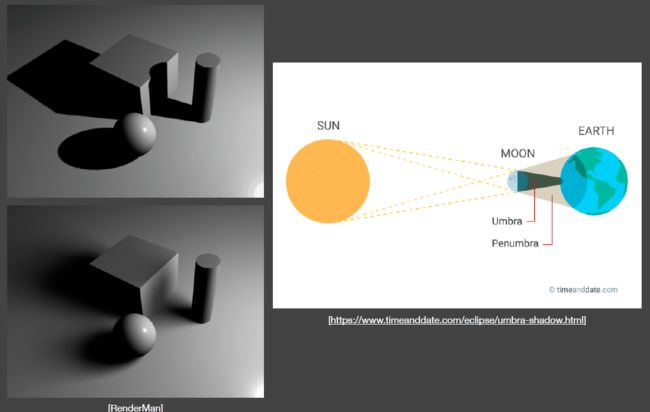
软阴影是从本影到没有阴影之间有一个半影区域,在这些区域看向光源,光源会被部分遮挡。
1、Percentage Closer Filtering (PCF)
-
Provides anti-aliasing at shadows’ edges
--Not for soft shadows (PCSS is, introducing later)
--Filtering the results of shadow comparisons
PCF是用来做抗锯齿(反走样),但是后来人们发现这个技术还可以做软阴影,于是有了PCSS
-
Why not filtering the shadow map?
--Texture filtering just averages color components, i.e. you’ll get blurred shadow map first
--Averaging depth values, then comparing, you still get a binary visibility
PCSS不是对渲染出来的阴影图做软阴影处理,也不是对shadow map做处理,而是在阴影判断的时候就做处理(类似于GAMES101中提到的做反走样的流程)
-
Solution [Reeves, SIGGARPH 87]
–Perform multiple (e.g. 7x7) depth comparisons for each fragment
–Then, averages results of comparisons
之前判断任何一个点在不在阴影里的时候,我们将shading point连向light算出深度去跟shadow map对应的这点的深度去比较。
在PCF的算法中,对于一个shading point,依然判断是否落在阴影里,但是投影到light之后不只是找shadow map对应点的像素,同时找shadow map对应该点的像素周围一圈的像素(如7×7),将这一圈的每一个像素深度值都与该shading point深度值去比较,由于每一次比较之后返回的值仅为0和1,做完比较之后把这值取平均,返回到这个点上。
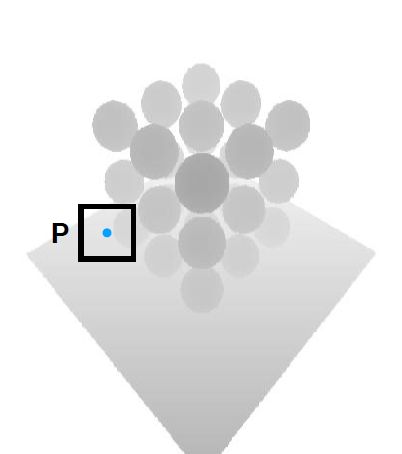
–e.g. for point P on the floor,
(1) compare its depth with all pixels in the red box, e.g. 3x3首先将shading point的点P深度值与shadow map中对应该像素以及周围3×3的每一个像素的深度值分别比较
(2) get the compared results, e.g.
1, 0, 1,
1, 0, 1,
1, 1, 0,然后得到一组返回值
(3) take avg. to get visibility, e.g. 0.667
将这组返回值取平均返回给点P
-
Does filtering size matter?
–Small -> sharper
–Large -> softer
如果卷积盒取小了边缘会很锐利,锯齿问题不会得到改善,卷积盒取大了虽然锯齿没了,但是图片也糊了。
-
Can we use PCF to achieve soft shadow effects?
软阴影的操作就可以通过对硬阴影取一个很大的卷积盒(filter)来实现
-
Key thoughts
–From hard shadows to soft shadows
–What’s the correct size to filter?
–Is it uniform?
2、Percentage Closer Soft Shadows
-
Key observation [Fernando et al.]
–Where is sharper? Where is softer?

物体离投影平面越近,则阴影越硬,离投影平面越远,则阴影越软。
-
Key conclusion
–Filter size <-> blocker distance
–More accurately, relative average projected blocker depth!
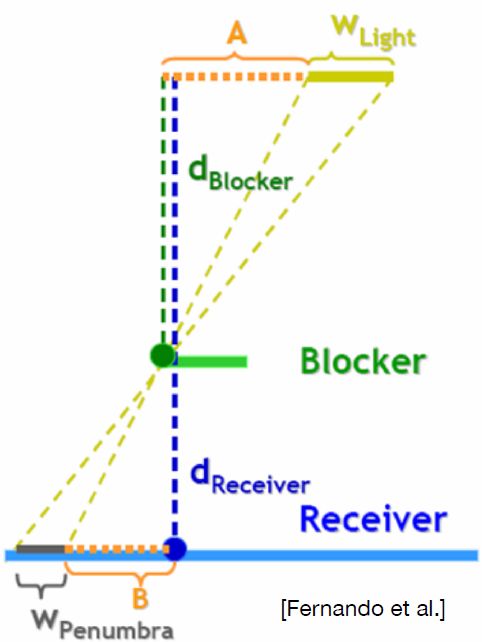
如上图,黄色的W是光源,中间的绿色点是投影物体(遮挡物),灰色W是软阴影区域,两个W及其连线组成了一对相似三角形,根据相似三角形原理可以求出软阴影区域WPenumbr。这个图可以很好地表明物体离投影平面越近,则阴影越硬,离投影平面越远,则阴影越软。
-
A mathematical “translation”
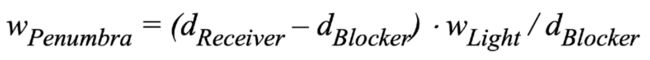
根据相似三角形将其软阴影用式子表示出来。
-
Now the only question:
–What’s the blocker depth dBlocker
卷积盒filter的大小取决于Light的大小和Blocker的大小。由于Blocker可能是很多不规则物体组成的,因此该处的Blocker要取平均:对于一个shading point来说,在一定的范围内,有多少可以在shadow map上挡住其的像素,这些像素记录的深度的平均值是多少。
-
The complete algorithm of PCSS
–Step 1: Blocker search
(getting the average blocker depth in a certain region)–Step 2: Penumbra estimation
(use the average blocker depth to determine filter size)–Step 3: Percentage Closer Filtering
-
Which region to perform blocker search?
–Can be set constant (e.g. 5x5), but can be better with heuristics
在shading point中,原本就是为了决定在一个shadow map周围多大的范围(filte)做PCF,为了知道这个信息,首先要知道average blocker depth是多少,为了知道这个信息,首先也应该先取一个区域去找average Blocker然后求depth,人们通常一开始固定一个范围大小(如5×5),另外还有更好的方法:
- Which region (on the shadow map) to perform blocker search?
--depends on the light size
--and receiver’s distance from the light
将shading point连向Light,就可以得到其在shadow map上的区域(如上图红色部分),通过这部分区域来确定filter。