生成两组相互独立服从标准正态分布的随机数(推导过程)
生成两组相互独立服从标准正态分布的随机数(推导过程)
-
- 预备知识:均匀分布的特殊地位
- 生成两组独立的服从标准正态分布的随机数
预备知识:均匀分布的特殊地位
设 F ( x ) F(x) F(x)满足:(1)单调不减(2) F ( − ∞ ) = 0 F(-\infty)=0 F(−∞)=0, F ( ∞ ) = 1 F(\infty)=1 F(∞)=1 (3)左连续。对于 0 ≤ y ≤ 1 0≤y≤1 0≤y≤1,定义 F − 1 ( y ) = i n f { x : F ( x ) > y } F^{-1}(y)=inf\{x:F(x)>y\} F−1(y)=inf{x:F(x)>y}为 F ( x ) F(x) F(x)的反函数
可见任何分布的分布函数均满足上面条件
若 ξ \xi ξ服从 F ( x ) F(x) F(x),记 θ = F ( ξ ) \theta=F(\xi) θ=F(ξ),可知 0 ≤ θ ≤ 1 0≤\theta≤1 0≤θ≤1
其分布函数:
F θ ( x ) = p ( θ < x ) = p ( F ( ξ ) < x ) = p ( ξ < F − 1 ( x ) ) = F ( F − 1 ( x ) ) = x F_\theta(x)=p(\theta
可得, θ \theta θ的分布函数:
F θ ( x ) = { 1 x>1 x 0≤x≤1 0 x<0 F_\theta(x)= \begin{cases} 1 & \text{x>1}\\ x & \text{0≤x≤1}\\ 0 & \text{x<0} \end{cases} Fθ(x)=⎩⎪⎨⎪⎧1x0x>10≤x≤1x<0
θ \theta θ的密度函数:
p θ ( x ) = { 1 0≤x≤1 0 其他 p_\theta(x)= \begin{cases} 1 & \text{0≤x≤1}\\ 0 & \text{其他} \end{cases} pθ(x)={100≤x≤1其他
所以 θ \theta θ服从0-1均匀分布
任意变量经过自身分布函数的变换后就变成了0-1均匀分布,相反,若 θ ∼ U [ 0 , 1 ] \theta\thicksim U[0,1] θ∼U[0,1],取 ξ = F − 1 ( θ ) \xi=F^{-1}(\theta) ξ=F−1(θ),其中 F − 1 ( x ) F^{-1}(x) F−1(x)是 ξ \xi ξ的分布函数的反函数,则此时 ξ \xi ξ服从相应的分布函数。因此,可由生成的一组服从 U [ 0 , 1 ] U[0,1] U[0,1]分布的变量 θ \theta θ,经过 F − 1 ( θ ) F^{-1}(\theta) F−1(θ)变换后生成服从相应分布的一组变量。
这是对可以写出分布函数并能写出分布函数反函数的一些随机变量,生成对应分布随机数值的一种方法。(1)生成[0,1]之间随机数;(2)写出要求分布的分布函数的反函数;(3)带入反函数求解。
例如指数分布:
ξ ∼ p ( x ) = { λ e − λ x x≥0, λ > 0 0 x<0 \xi\thicksim p(x)= \begin{cases} \lambda e^{-\lambda x} & \text{x≥0, }\lambda>0\\ 0 & \text{x<0} \end{cases} ξ∼p(x)={λe−λx0x≥0, λ>0x<0
F ( x ) = { 1 − e − λ x x≥0, λ > 0 0 x<0 F(x)= \begin{cases} 1-e^{-\lambda x} & \text{x≥0, }\lambda>0\\ 0 & \text{x<0} \end{cases} F(x)={1−e−λx0x≥0, λ>0x<0
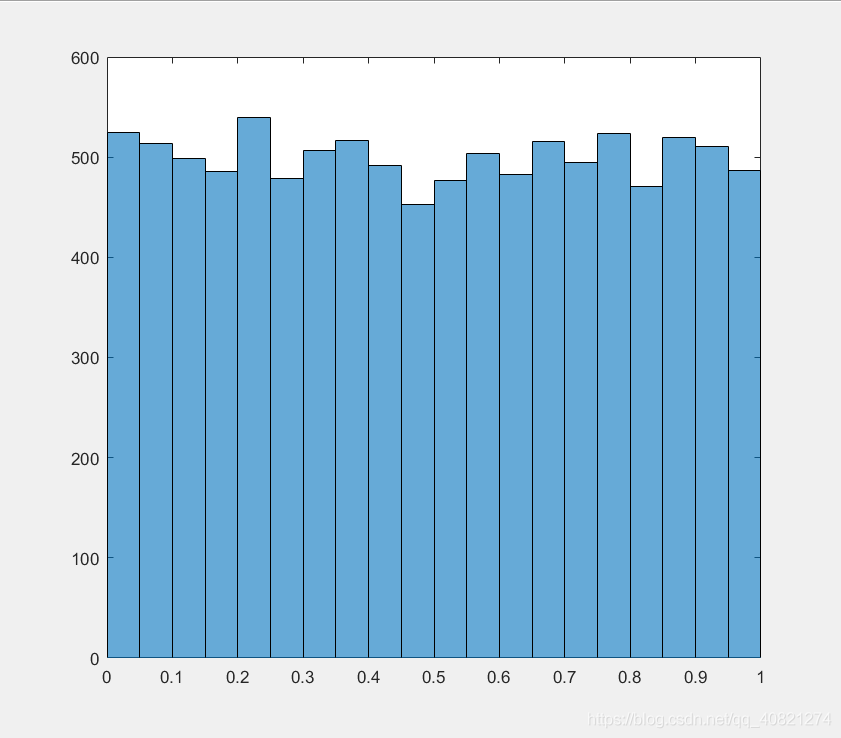
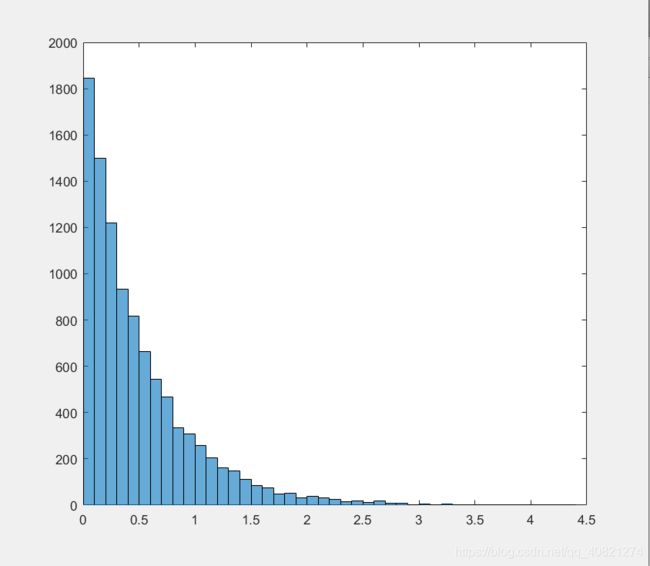
生成 θ ∼ U [ 0 , 1 ] \theta\thicksim U[0,1] θ∼U[0,1]的一组随机数(上图),将该随机数进行变换: x = − 1 / 2 l n ( 1 − θ ) x=-1/2ln(1-\theta) x=−1/2ln(1−θ) ,如果这里参数取 λ = 2 \lambda=2 λ=2。生成的新的一组数符合 λ = 2 \lambda=2 λ=2的指数分布(下图)。
而对于标准正态分布 N ( 0 , 1 ) N(0,1) N(0,1),它的密度函数:
p ( x ) = 1 2 π e − x 2 2 p(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} p(x)=2π1e−2x2
由于正态分布的分布函数没有解析式,难以根据分布函数求反函数来获取相应的随机数,这里提出新的方法。
生成两组独立的服从标准正态分布的随机数
背景题目:
设 ξ \xi ξ、 η \eta η独立同分布于 N ( 0 , 1 ) N(0,1) N(0,1),即:
p ξ ( x ) = 1 2 π e − x 2 2 p η ( y ) = 1 2 π e − y 2 2 p_\xi(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\\ p_\eta(y)=\frac{1}{\sqrt{2\pi}}e^{-\frac{y^2}{2}} pξ(x)=2π1e−2x2pη(y)=2π1e−2y2
两者相互独立,联合密度函数等于边际密度函数乘积:
( ξ , η ) ∼ p ( x , y ) = 1 2 π e − x 2 + y 2 2 (\xi,\eta)\thicksim p(x,y)=\frac{1}{{2\pi}}e^{-\frac{x^2+y^2}{2}} (ξ,η)∼p(x,y)=2π1e−2x2+y2
设变量 ( ρ , ϕ ) (\rho,\phi) (ρ,ϕ)满足:
( ρ , ϕ ) = f ( ξ , η ) : { ρ = ( ξ 2 + η 2 ) 1 / 2 ϕ = t a n − 1 ( η / ξ ) (\rho,\phi)=f(\xi,\eta): \begin{cases} \rho=(\xi^2+\eta^2)^{1/2}\\ \phi=tan^{-1}(\eta/\xi) \end{cases} (ρ,ϕ)=f(ξ,η):{ρ=(ξ2+η2)1/2ϕ=tan−1(η/ξ)
则:
( ξ , η ) = f − 1 ( ρ , ϕ ) = h ( ρ , ϕ ) : { η = ρ c o s ϕ ξ = ρ s i n ϕ (\xi,\eta)=f^{-1}(\rho,\phi)=h(\rho,\phi): \begin{cases} \eta=\rho cos\phi\\ \xi=\rho sin\phi \end{cases} (ξ,η)=f−1(ρ,ϕ)=h(ρ,ϕ):{η=ρcosϕξ=ρsinϕ
雅可比行列式:
∣ J ∣ = ∣ ∂ h 1 ∂ ρ ∂ h 1 ∂ ϕ ∂ h 2 ∂ ρ ∂ h 1 ∂ ϕ ∣ = ∣ c o s θ − r s i n θ s i n θ r c o s θ ∣ = r |J|=\begin{vmatrix}\frac{\partial h_1}{\partial\rho} & \frac{\partial h_1}{\partial\phi} \\\frac{\partial h_2}{\partial\rho} &\frac{\partial h_1}{\partial\phi} \end{vmatrix}=\begin{vmatrix}cos\theta & -rsin\theta \\sin\theta & rcos\theta \end{vmatrix}=r ∣J∣=∣∣∣∣∣∂ρ∂h1∂ρ∂h2∂ϕ∂h1∂ϕ∂h1∣∣∣∣∣=∣∣∣∣cosθsinθ−rsinθrcosθ∣∣∣∣=r
可求得 ( ρ , ϕ ) (\rho,\phi) (ρ,ϕ)联合密度函数:
( ρ , ϕ ) ∼ q ( r , θ ) = p ( x , y ) ∣ J ∣ = 1 2 π e − x 2 + y 2 2 ∗ r = 1 2 π e − ( r c o s θ ) 2 + ( r s i n θ ) 2 2 ∗ r = 1 2 π e − r 2 2 ∗ r = r e − r 2 2 ∗ 1 2 π = q ρ ( r ) ∗ q ϕ ( θ ) (\rho,\phi)\thicksim q(r,\theta)=p(x,y)|J|\\ =\frac{1}{{2\pi}}e^{-\frac{x^2+y^2}{2}}*r\\ =\frac{1}{{2\pi}}e^{-\frac{(rcos\theta)^2+(rsin\theta)^2}{2}}*r\\ =\frac{1}{2\pi}e^{-\frac{r^2}{2}}*r\\ =re^{-\frac{r^2}{2}}*\frac{1}{2\pi}\\ =q_\rho(r)*q_\phi(\theta) (ρ,ϕ)∼q(r,θ)=p(x,y)∣J∣=2π1e−2x2+y2∗r=2π1e−2(rcosθ)2+(rsinθ)2∗r=2π1e−2r2∗r=re−2r2∗2π1=qρ(r)∗qϕ(θ)
恰好是两个相互独立的分布的乘积:瑞利分布和 U [ 0 , 2 π ] U[0,2\pi] U[0,2π]
瑞利分布和均匀分布可以根据 前面均匀分布的特殊地位,首先生成两组0-1均匀分布的变量 u 1 u_1 u1和 u 2 u_2 u2,通过瑞利分布函数、 U [ 0 , 2 π ] U[0,2\pi] U[0,2π]分布函数反函数的变换使得两组数分别满足瑞利分布和 U [ 0 , 2 π ] U[0,2\pi] U[0,2π]分布。再将两组数根据如下变换(二维向量的变换):
{ ξ = ρ c o s ϕ η = ρ s i n ϕ \begin{cases} \xi=\rho cos\phi\\ \eta=\rho sin\phi \end{cases} {ξ=ρcosϕη=ρsinϕ
得到两组独立的标准正态分布
具体操作如下:
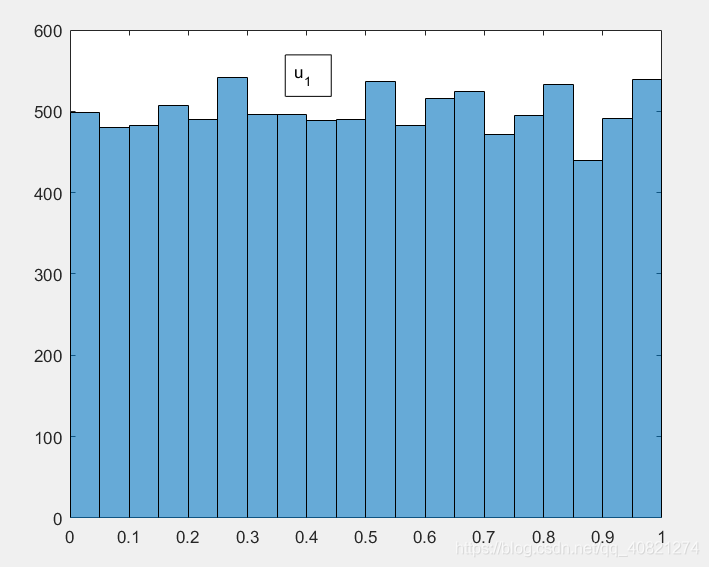
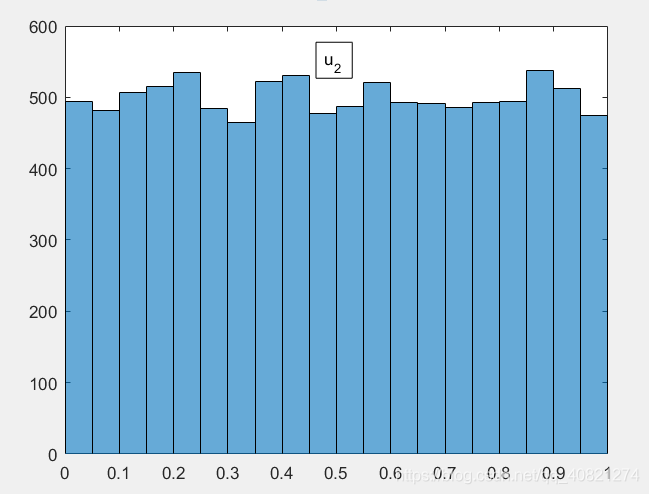
- 生成两组0-1均匀分布随机数 u 1 u_1 u1和 u 2 u_2 u2
- 已求得瑞利分布和 U [ 0 , 2 π ] U[0,2\pi] U[0,2π]的密度函数,通过积分求他们的分布函数:
瑞利分布(r>0):
F ( r ) = 1 − e − r 2 2 F(r)=1-e^{-\frac{r^2}{2}} F(r)=1−e−2r2
U [ 0 , 2 π ] U[0,2\pi] U[0,2π] 均匀分布( 0 ≤ θ ≤ 2 π 0≤\theta≤2\pi 0≤θ≤2π):
G ( θ ) = θ 2 π G(\theta)={\frac{\theta}{2\pi}} G(θ)=2πθ
- 分别求他们的反函数:
瑞利分布:
F − 1 ( u 1 ) = [ − 2 l n ( 1 − u 1 ) ] 1 / 2 F^{-1}(u_1)=[-2ln(1-u_1)]^{1/2} F−1(u1)=[−2ln(1−u1)]1/2
U [ 0 , 2 π ] U[0,2\pi] U[0,2π] 均匀分布:
G − 1 ( u 2 ) = 2 π u 2 G^{-1}(u_2)=2\pi u_2 G−1(u2)=2πu2
- 再代入如下变换:
{ ξ = ρ c o s ϕ η = ρ s i n ϕ \begin{cases} \xi=\rho cos\phi\\ \eta=\rho sin\phi \end{cases} {ξ=ρcosϕη=ρsinϕ
得到:
ξ = [ − 2 l n ( 1 − u 1 ) ] 1 / 2 c o s ( 2 π u 2 ) η = [ − 2 l n ( 1 − u 1 ) ] 1 / 2 s i n ( 2 π u 2 ) \xi=[-2ln(1-u_1)]^{1/2}cos(2\pi u_2)\\ \eta=[-2ln(1-u_1)]^{1/2}sin(2\pi u_2) ξ=[−2ln(1−u1)]1/2cos(2πu2)η=[−2ln(1−u1)]1/2sin(2πu2)
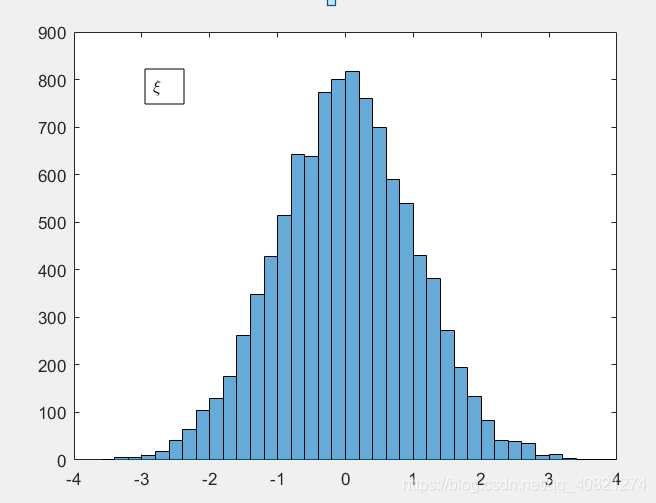
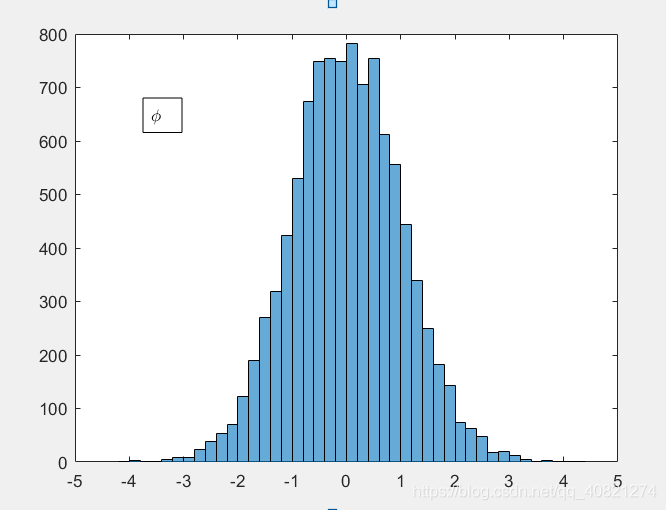
则 ξ \xi ξ和 ϕ \phi ϕ是相互独立的 N ( 0 , 1 ) N(0,1) N(0,1)随机数。
也可直接写为:
ξ = [ − 2 l n ( u 1 ) ] 1 / 2 c o s ( 2 π u 2 ) η = [ − 2 l n ( u 1 ) ] 1 / 2 s i n ( 2 π u 2 ) \xi=[-2ln(u_1)]^{1/2}cos(2\pi u_2)\\ \eta=[-2ln(u_1)]^{1/2}sin(2\pi u_2) ξ=[−2ln(u1)]1/2cos(2πu2)η=[−2ln(u1)]1/2sin(2πu2)
u 1 u_1 u1和 u 2 u_2 u2均是0到1区间内, ( 1 − u 1 ) (1-u_1) (1−u1)和 u 1 u_1 u1生成的随机数是一样的
试验如下(matlab):
u1=rand(1,10000)
u2=rand(1,10000)
y1=sqrt(-2*log(1-u1)).*cos(2*pi*u2)
y2=sqrt(-2*log(1-u1)).*sin(2*pi*u2)