吴恩达深度学习第一课第四周编程作业（1）

构建深层神经网络：一步一步

欢迎参加第4周的作业（第1部分，共2部分）！之前，您训练了一个具有单个隐藏层的两层神经网络。本周，你将建立一个深层次的神经网络，你想要多少层都行！

-在本笔记本中，您将实现构建深度神经网络所需的所有功能。
-在下一个作业中，您将使用这些函数来构建用于图像分类的深层神经网络。

在本次作业结束时，您将能够：

-使用像ReLU这样的非线性单位来改进你的模型
-建立一个更深层次的神经网络（有一个以上的隐层）
-实现一个易于使用的神经网络类

符号：

上标[]  表示与ℎ  图层。
例子：[]  是ℎ  图层激活。[]  以及[]  是ℎ  图层参数。
上标()  表示与ℎ  例子。
例子：()  是ℎ  培训示例。
小写字母  表示ℎ  向量的输入。
例子：[]  表示ℎ  进入ℎ  层的激活。

我们开始吧！

1-包装

首先，导入此任务期间需要的所有包。
numpy是使用Python进行科学计算的主要包。
matplotlib是一个用Python绘制图形的库。
dnn_utils为这个笔记本提供了一些必要的功能。
testCases提供了一些测试用例来评估函数的正确性
seed（1）用于保持所有随机函数调用的一致性。它有助于给你的工作打分。请不要换种子！

import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases import *
from dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

2-轮廓

为了建立你的神经网络，你将实现几个“辅助函数”。这些辅助函数将在下一个作业中用来建立一个两层神经网络和一个L层神经网络。
每个小助手函数都有详细的说明，指导您完成必要的步骤。以下是本作业步骤的概要：

·初始化两层网络和层神经网络
·实现前向传播模块（如下图中紫色所示）
	-完成层正向传播步骤的线性部分（导致[] ).
	-为您提供激活功能（relu/sigmoid）
	-将前两个步骤组合成一个新的[线性->激活]正向函数。
	-将[LINEAR->RELU]正向函数L-1叠加一次（对于第1层到第1层），并在末尾添加一个[LINEAR->SIGMOID]（对于最后一层） ). 这将为您提供一个新的L_model_forward函数。
·计算损失
·实现反向传播模块（下图中用红色表示）
	-完成层反向传播步骤的线性部分
	-为您提供激活功能的梯度（relu_backward/sigmoid_backward）
	-将前两个步骤组合成一个新的[线性->激活]向后函数
	-将[LINEAR->RELU]向后叠加L-1次，并在新的L_模型向后函数中向后添加[LINEAR->SIGMOID]
·最后，更新参数

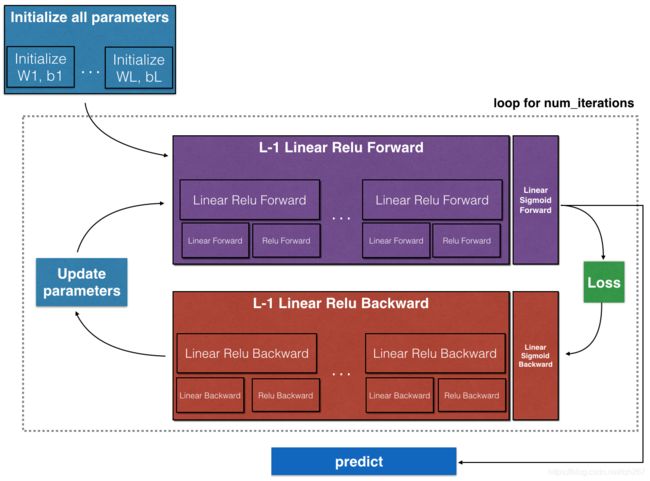
注：
对于每个前向函数，都有一个对应的后向函数。这就是为什么在forward模块的每一步中，您都会在缓存中存储一些值。这些缓存值对于计算渐变非常有用。
在反向传播模块中，您可以使用缓存来计算梯度。别担心，这项作业将向你展示如何执行这些步骤！

3-初始化

您将编写两个helper函数来初始化模型的参数。第一个函数将用于初始化两层模型的参数。第二种方法将这个初始化过程推广到 层。

3.1-2层神经网络

练习1-初始化参数

创建并初始化两层神经网络的参数。
说明：

·模型的结构是：LINEAR->RELU->LINEAR->SIGMOID。
·对权重矩阵使用此随机初始化：np.random.randn（shape）*0.01，形状正确
·对偏差使用零初始化：np.zeros（shape）

# GRADED FUNCTION: initialize_parameters

def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer
    
    Returns:
    parameters -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    
    np.random.seed(1)
    
    #(≈ 4 lines of code)
    # W1 = ...
    # b1 = ...
    # W2 = ...
    # b2 = ...
    # YOUR CODE STARTS HERE
    W1 = np.random.randn(n_h,n_x)*0.01
    b1 = np.zeros((n_h,1))
    W2 = np.random.randn(n_y,n_h)*0.01
    b2 = np.zeros((n_y,1))
    
    # YOUR CODE ENDS HERE
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters    

parameters = initialize_parameters(3,2,1)

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

initialize_parameters_test(initialize_parameters)

运行结果：

W1 = [[ 0.01624345 -0.00611756 -0.00528172]
 [-0.01072969  0.00865408 -0.02301539]]
b1 = [[0.]
 [0.]]
W2 = [[ 0.01744812 -0.00761207]]
b2 = [[0.]]
 All tests passed.

笔记：
使用numpy.zeros()函数时，传入的参数是两个，必须用小括号括起来，例如：b2 = np.zeros((n_y,1))

3.2-L层神经网络

对于较深的L层神经网络，由于其权值矩阵和偏差向量较多，初始化比较复杂。完成initialize_parameters_deep函数时，应确保每个层之间的尺寸匹配。记得[] 是层中的单元数 . 例如，如果输入的大小 is（12288,209）（=209例）然后：

记住当你计算+ 在python中，它执行广播。例如，如果：
那么+ 将：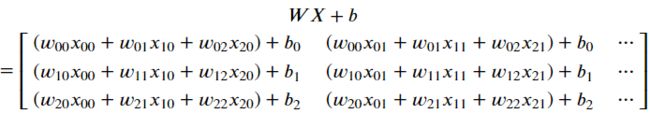

练习2-初始化参数

实现L层神经网络的初始化。
说明：

-模型的结构是*[LINEAR->RELU]×  (L-1）->LINEAR->SIGMOID*。也就是说，它有−1层使用ReLU激活功能，然后输出层使用sigmoid激活功能。
-对权重矩阵使用随机初始化。使用np.random.randn（shape）*0.01。
-对偏差使用零初始化。使用np.zeros（shape）。
-你会储存[] , 在一个可变层中，不同层中的单位数。例如，上周的平面数据分类模型的层dims应该是[2,4,1]：有两个输入，一个隐藏层有4个隐藏单元，一个输出层有1个输出单元。这意味着W1的形状是（4,2），b1是（4,1），W2是（1,4），b2是（1,1）。现在你要把它推广到  层！
-以下是实现=1（单层神经网络）。它将启发您实现一般情况（L层神经网络）。

if L == 1:
      parameters["W" + str(L)] = np.random.randn(layer_dims[1], layer_dims[0]) * 0.01
      parameters["b" + str(L)] = np.zeros((layer_dims[1], 1))

练习：

# GRADED FUNCTION: initialize_parameters_deep

def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layer_dims) # number of layers in the network

    for l in range(1, L):
        #(≈ 2 lines of code)
        # parameters['W' + str(l)] = ...
        # parameters['b' + str(l)] = ...
        # YOUR CODE STARTS HERE
        parameters["W" + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) * 0.01
        parameters["b" + str(l)] = np.zeros((layer_dims[l], 1))
        # YOUR CODE ENDS HERE
        
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l - 1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

        
    return parameters

运行：

parameters = initialize_parameters_deep([5,4,3])

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

initialize_parameters_deep_test(initialize_parameters_deep)

运行结果：

W1 = [[ 0.01788628  0.0043651   0.00096497 -0.01863493 -0.00277388]
 [-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
 [-0.01313865  0.00884622  0.00881318  0.01709573  0.00050034]
 [-0.00404677 -0.0054536  -0.01546477  0.00982367 -0.01101068]]
b1 = [[0.]
 [0.]
 [0.]
 [0.]]
W2 = [[-0.01185047 -0.0020565   0.01486148  0.00236716]
 [-0.01023785 -0.00712993  0.00625245 -0.00160513]
 [-0.00768836 -0.00230031  0.00745056  0.01976111]]
b2 = [[0.]
 [0.]
 [0.]]
 All tests passed.

笔记（思考）：
由此可知，权值矩阵W和偏差向量b的维度大小都和每层神经元个数相关，其中Wi(a,b)，a=当前层神经元个数，b = 前一层神经元个数，bi(c,1),c = 当前层的神经元个数

4-正向传播模块

4.1-线性向前

既然已经初始化了参数，就可以进行前向传播模块了。首先实现一些基本函数，稍后在实现模型时可以再次使用这些函数。现在，您将按以下顺序完成三个函数：

线性的
线性->激活，激活为ReLU或Sigmoid。
[线性->RELU]×  (L-1）->线性->SIGMOID（整个模型）

线性正向模块（在所有示例中矢量化）计算以下等式：

当A[0]时其 = X

练习3-线性向前

建立正向传播的线性部分。
提醒：这个单位的数学表示是[]=[][−1]+[] . 您可能还发现np.dot（）很有用。如果尺寸不匹配，打印W.shape可能会有所帮助。

# GRADED FUNCTION: linear_forward

def linear_forward(A, W, b):
    """
   实现层正向传播的线性部分。
	参数：
	A——上一层的激活（或输入数据）：（上一层的大小，示例数）
	W——权重矩阵：形状的numpy数组（当前层的大小，上一层的大小）
	b——偏置矢量，形状的numpy数组（当前层的大小，1）
	返回：
	Z——激活函数的输入，也称为预激活参数
	cache—包含“a”、“W”和“b”的python元组；为有效计算后向传递而存储
    """
    
    #(≈ 1 line of code)
    # Z = ...
    # YOUR CODE STARTS HERE
    Z = np.dot(W,A) + b
    
    # YOUR CODE ENDS HERE
    cache = (A, W, b)
    
    return Z, cache

运行：

t_A, t_W, t_b = linear_forward_test_case()
t_Z, t_linear_cache = linear_forward(t_A, t_W, t_b)
print("Z = " + str(t_Z))

linear_forward_test(linear_forward)

运行结果：

Z = [[ 3.26295337 -1.23429987]]
 All tests passed.

笔记：
在计算Z时，使用np.dot()函数，参数传入分别时W，A，再和b进行广播

4.2-正向线性激活

在本笔记本中，您将使用两个激活功能：

·Sigmoid：()=(+)=1/(1+^−(+)) . 我们为您提供了sigmoid函数，它返回两项：激活值“a”和包含“Z”的“cache”（这是我们将输入到相应的backward函数中的内容）。要使用它，您只需执行：
A, activation_cache= sigmoid（Z）
·ReLU：ReLU的数学公式是=()=(0,) . 你已经被提供了relu功能。此函数返回两项：激活值“A”和包含“Z”的“cache”（这是您将输入到相应的backward函数的内容）。要使用它，您只需执行：
A, activation_cache = relu(Z)

为了方便起见，我们将两个函数（线性和激活）组合成一个函数（线性->激活）。因此，您将实现一个函数，该函数执行线性前进步骤，然后执行激活前进步骤。

# GRADED FUNCTION: linear_activation_forward

def linear_activation_forward(A_prev, W, b, activation):
    """
    实现线性->激活层的前向传播
参数：
	A_prev—上一层的激活（或输入数据）：（上一层的大小，示例数）
	W——权重矩阵：形状的numpy数组（当前层的大小，上一层的大小）
	b——偏置矢量，形状的numpy数组（当前层的大小，1）
	激活——这个层中要使用的激活，以文本字符串形式存储：“sigmoid”或“relu”
	return：
	A——激活函数的输出，也称为激活后值
	cache——一个包含“线性缓存”和“激活缓存”的python元组；为有效计算后向传递而存储
    """
    
    if activation == "sigmoid":
        #(≈ 2 lines of code)
        # Z, linear_cache = ...
        # A, activation_cache = ...
        # YOUR CODE STARTS HERE
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache= sigmoid(Z)
        
        # YOUR CODE ENDS HERE
    
    elif activation == "relu":
        #(≈ 2 lines of code)
        # Z, linear_cache = ...
        # A, activation_cache = ...
        # YOUR CODE STARTS HERE
        Z, linear_cache = linear_forward(A_prev,W,b)
        A, activation_cache= relu(Z)
        
        # YOUR CODE ENDS HERE
    cache = (linear_cache, activation_cache)

    return A, cache

运行：

t_A_prev, t_W, t_b = linear_activation_forward_test_case()

t_A, t_linear_activation_cache = linear_activation_forward(t_A_prev, t_W, t_b, activation = "sigmoid")
print("With sigmoid: A = " + str(t_A))

t_A, t_linear_activation_cache = linear_activation_forward(t_A_prev, t_W, t_b, activation = "relu")
print("With ReLU: A = " + str(t_A))

linear_activation_forward_test(linear_activation_forward)

运行结果：

With sigmoid: A = [[0.96890023 0.11013289]]
With ReLU: A = [[3.43896131 0.        ]]
 All tests passed.

注：在深度学习中，“[线性->激活]”计算被算作神经网络中的一层，而不是两层。
笔记：
本次练习我了解了如何实现将relu和sigmoid函数整合在一个函数中

4.3-L层模型

在实现 层多层神经网络中，你需要一个复制上一个的函数（用RELU进行线性激活）−1次，然后用sigmoid向前一次线性激活。

练习5-L_model_forward

实现了上述模型的前向传播。
说明：在下面的代码中，变量AL表示[]=([])=([][−1]+[]) . (这有时也称为Yhat，即̂ .)
提示：

-使用以前编写的函数
-使用for循环复制[LINEAR->RELU]（L-1）次
-别忘了跟踪“cache”列表中的缓存。要向列表中添加新值c，可以使用list.append（c）。

# GRADED FUNCTION: L_model_forward

def L_model_forward(X, parameters):
    """
   	[LINEAR->RELU]*（L-1）->LINEAR->SIGMOID计算的实现前向传播
	参数：
	X—数据，形状的numpy数组（输入大小，示例数）
	parameters—initialize\u parameters\u deep（）的输出
	返回：
	AL——最后一次激活后的值
	缓存--包含以下内容的缓存列表：
	linear_activation_forward（）的每个缓存（有L-1个，索引范围从0到L-1）
    """

    caches = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network
    
    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    # The for loop starts at 1 because layer 0 is the input
    for l in range(1, L):
        A_prev = A 
        #(≈ 2 lines of code)
        # A, cache = ...
        # caches ...
        # YOUR CODE STARTS HERE
        A,cache = linear_activation_forward(A_prev,parameters["W" + str(l)],parameters["b" + str(l)],"relu")
        caches.append(cache) 
        # YOUR CODE ENDS HERE
    
    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    #(≈ 2 lines of code)
    # AL, cache = ...
    # caches ...
    # YOUR CODE STARTS HERE
    AL,cache = linear_activation_forward(A,parameters["W" + str(L)],parameters["b" + str(L)],"sigmoid")
    caches.append(cache)
    
    # YOUR CODE ENDS HERE
          
    return AL, caches

运行：

t_X, t_parameters = L_model_forward_test_case_2hidden()
t_AL, t_caches = L_model_forward(t_X, t_parameters)

print("AL = " + str(t_AL))

L_model_forward_test(L_model_forward)

运行结果：

AL = [[0.03921668 0.70498921 0.19734387 0.04728177]]
 All tests passed.

笔记：
该练习实现了前L-1次隐含层中的Relu激活以及最后一次的Sigmoid激活，L = len(parameters) // 2 是因为parameters中既有W也有b,他们成对出现，所以parameters是2L长度，并且下标是从1~L+1。*
令人惊叹的！您已经实现了一个完整的前向传播，它接受输入X并输出一个行向量[] 包含你的预测。它还将所有中间值记录在“缓存”中。使用[] , 你可以计算你的预测的成本。

5-成本函数

现在您可以实现正向和反向传播了！您需要计算成本，以便检查您的模型是否真正在学习。

练习6-计算成本

计算交叉熵代价 , 使用以下公式：

# GRADED FUNCTION: compute_cost

def compute_cost(AL, Y):
    """
    实现等式（7）定义的成本函数。
	参数：
	AL—与标签预测相对应的概率向量，shape（1，示例数）
	Y—真“标签”向量（例如：非cat包含0，cat包含1），形状（1，示例数）
	返回：
	成本——交叉熵成本
    """
    
    m = Y.shape[1]

    # Compute loss from aL and y.
    # (≈ 1 lines of code)
    # cost = ...
    # YOUR CODE STARTS HERE
    
    cost = (-1/m)*np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))
    # YOUR CODE ENDS HERE
    
    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).

    
    return cost

运行：

t_Y, t_AL = compute_cost_test_case()
t_cost = compute_cost(t_AL, t_Y)

print("Cost: " + str(t_cost))

compute_cost_test(compute_cost)

运行结果:

Cost: 0.2797765635793422
 All tests passed.

笔记：
此处应该强调在计算Ylog（AL）时，使用的是号而不是numpy.dot()这是因为Y和AL都是一个维度为（1，训练数）的向量，所以可直接使用*实现每一项对应相乘。

6-反向传播模块

正如您对前向传播所做的那样，您将实现反向传播的助手函数。请记住，反向传播用于计算损失函数相对于参数的梯度。
提醒：

图3:LINEAR->RELU->LINEAR->SIGMOID的正向和反向传播
紫色块表示正向传播，红色块表示反向传播。

现在，与正向传播类似，您将分三步构建反向传播：

1.线性向后
2.线性->反向激活，激活计算ReLU或sigmoid激活的导数
3.[线性->RELU]×  (L-1）->线性->SIGMOID 反向（整个模型）

在下一个练习中，您需要记住：

-b是一个有1列和n行的矩阵（np.ndarray），即：b=[[1.0]，[2.0]]（记住b是一个常数）
-np.sum对数组的元素执行求和
-axis=1或axis=0分别指定是按行还是按列执行求和
-keepdims指定是否必须保留矩阵的原始维度。
-看下面的例子来证明：

A = np.array([[1, 2,3], [3, 4,5]])
print(A.shape)
print('axis=1 and keepdims=True')
print(np.sum(A, axis=1, keepdims=True))
print('axis=1 and keepdims=False')
print(np.sum(A, axis=1, keepdims=False))
print('axis=0 and keepdims=True')
print(np.sum(A, axis=0, keepdims=True))
print('axis=0 and keepdims=False')
print(np.sum(A, axis=0, keepdims=False))

运行结果：

(2, 3)
axis=1 and keepdims=True
[[ 6]
 [12]]
axis=1 and keepdims=False
[ 6 12]
axis=0 and keepdims=True
[[4 6 8]]
axis=0 and keepdims=False
[4 6 8]

笔记：
此例可知np.sum,()配合属性axis，keepdims的作用

6.1-线性向后

对于层 , 线性部分是：[]=[][−1]+[] (然后激活）。
假设你已经计算了导数[]. 你想得到什么([],[],[−1]) .

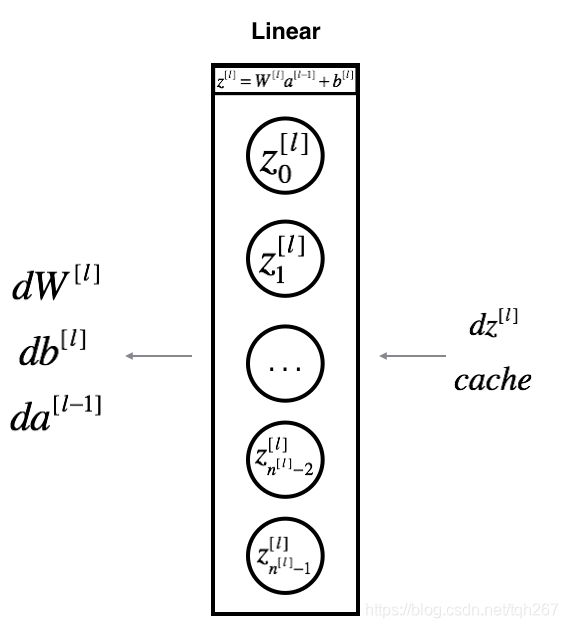
三个输出([],[],[−1] ）使用输入进行计算[] .
以下是您需要的公式：

练习7-直线向后

使用上面的3个公式来实现linear_backward（）。
提示：
在numpy中，您可以使用A.T或A.transpose（）获得数据数组A的转置

# GRADED FUNCTION: linear_backward

def linear_backward(dZ, cache):
    """
    实现单个层（层l）反向传播的线性部分
	参数：
	dZ——成本相对于线性输出的梯度（当前层l）
	cache—来自当前层中前向传播的值的元组（A\u prev，W，b）
	返回：
	dA_prev——相对于激活（前一层l-1）的成本梯度，与A_prev的形状相同
	dW——成本相对于W（当前层l）的梯度，形状和W相同
	db——成本相对于b（当前层l）的梯度，与b的形状相同
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    ### START CODE HERE ### (≈ 3 lines of code)
    # dW = ...
    # db = ... sum by the rows of dZ with keepdims=True
    # dA_prev = ...
    # YOUR CODE STARTS HERE
    dW = (1/m)*np.dot(dZ,A_prev.T)
    db = (1/m)*np.sum(dZ,axis = 1,keepdims = True)
    dA_prev = np.dot(W.T,dZ)
    # YOUR CODE ENDS HERE
    
    return dA_prev, dW, db

运行：

t_dZ, t_linear_cache = linear_backward_test_case()
t_dA_prev, t_dW, t_db = linear_backward(t_dZ, t_linear_cache)

print("dA_prev: " + str(t_dA_prev))
print("dW: " + str(t_dW))
print("db: " + str(t_db))

linear_backward_test(linear_backward)

运行结果：

dA_prev: [[-1.15171336  0.06718465 -0.3204696   2.09812712]
 [ 0.60345879 -3.72508701  5.81700741 -3.84326836]
 [-0.4319552  -1.30987417  1.72354705  0.05070578]
 [-0.38981415  0.60811244 -1.25938424  1.47191593]
 [-2.52214926  2.67882552 -0.67947465  1.48119548]]
dW: [[ 0.07313866 -0.0976715  -0.87585828  0.73763362  0.00785716]
 [ 0.85508818  0.37530413 -0.59912655  0.71278189 -0.58931808]
 [ 0.97913304 -0.24376494 -0.08839671  0.55151192 -0.10290907]]
db: [[-0.14713786]
 [-0.11313155]
 [-0.13209101]]
 All tests passed.

笔记：
该练习进一步了解了反向传播中各个参数梯度的计算，关键在于如何将公式转换为代码，理清各矩阵的维度

6.2-线性激活

接下来，您将创建一个合并两个助手函数的函数：linear_backward和激活的backward step linear_activation_backward。
为了帮助您实现linear_activation_backward，提供了两个向后函数：

sigmoid_backward：实现sigmoid单元的反向传播。你可以这样称呼它：
	dZ = sigmoid_backward(dA, activation_cache)
relu_backward：实现relu单元的反向传播。你可以这样称呼它：
	dZ = relu_backward(dA, activation_cache)

如果(.) 是激活函数，sigmoid_backward和relu_backward计算

练习8-linear_activation_backward

实现线性->激活层的反向传播。

# GRADED FUNCTION: linear_activation_backward

def linear_activation_backward(dA, cache, activation):
    """
    实现线性->激活层的反向传播。
	参数：
	dA——电流层l的激活后梯度
	cache—我们存储的用于高效计算反向传播的值的元组（线性\u cache、激活\u cache）
	激活——这个层中要使用的激活，以文本字符串形式存储：“sigmoid”或“relu”
	返回：
	dA_prev——相对于激活（前一层l-1）的成本梯度，与A_prev的形状相同
	dW——成本相对于W（当前层l）的梯度，形状和W相同
	db——成本相对于b（当前层l）的梯度，与b的形状相同
    """
    linear_cache, activation_cache = cache
    
    if activation == "relu":
        #(≈ 2 lines of code)
        # dZ =  ...
        # dA_prev, dW, db =  ...
        # YOUR CODE STARTS HERE
        dZ = relu_backward(dA,activation_cache)
        dA_prev,dW,db = linear_backward(dZ,linear_cache)
        # YOUR CODE ENDS HERE
        
    elif activation == "sigmoid":
        #(≈ 2 lines of code)
        # dZ =  ...
        # dA_prev, dW, db =  ...
        # YOUR CODE STARTS HERE
        dZ = sigmoid_backward(dA,activation_cache)
        dA_prev,dW,db = linear_backward(dZ,linear_cache)
        
        # YOUR CODE ENDS HERE
    
    return dA_prev, dW, db

运行：

t_dAL, t_linear_activation_cache = linear_activation_backward_test_case()

t_dA_prev, t_dW, t_db = linear_activation_backward(t_dAL, t_linear_activation_cache, activation = "sigmoid")
print("With sigmoid: dA_prev = " + str(t_dA_prev))
print("With sigmoid: dW = " + str(t_dW))
print("With sigmoid: db = " + str(t_db))

t_dA_prev, t_dW, t_db = linear_activation_backward(t_dAL, t_linear_activation_cache, activation = "relu")
print("With relu: dA_prev = " + str(t_dA_prev))
print("With relu: dW = " + str(t_dW))
print("With relu: db = " + str(t_db))

linear_activation_backward_test(linear_activation_backward)

运行结果：

With sigmoid: dA_prev = [[ 0.11017994  0.01105339]
 [ 0.09466817  0.00949723]
 [-0.05743092 -0.00576154]]
With sigmoid: dW = [[ 0.10266786  0.09778551 -0.01968084]]
With sigmoid: db = [[-0.05729622]]
With relu: dA_prev = [[ 0.44090989  0.        ]
 [ 0.37883606  0.        ]
 [-0.2298228   0.        ]]
With relu: dW = [[ 0.44513824  0.37371418 -0.10478989]]
With relu: db = [[-0.20837892]]
 All tests passed.

笔记：
该练习借助前面编写好的linear_backward(dZ,cache)函数实现sigmoid和relu不同的反向传播

6.3-L_Model 向后

现在您将实现整个网络的向后功能！
回想一下，当您实现L_model_forward函数时，在每次迭代中，您存储了一个包含（X、W、b和z）的缓存。在反向传播模块中，您将使用这些变量来计算梯度。因此，在L_model_backward函数中，您将从层开始向后遍历所有隐藏层 . 在每个步骤中，您将使用层的缓存值 通过层反向传播 . 下面的图5显示了向后传递。
我们需要计算dAL，我们可以使用下面的代码来计算它：
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

练习9-L_model_backward
为*[LINEAR->RELU]实现反向传播× (L-1）->线性->SIGMOID。

# GRADED FUNCTION: L_model_backward

def L_model_backward(AL, Y, caches):
    """
    对[LINEAR->RELU]*（L-1）->LINEAR->SIGMOID组实现反向传播
	参数：
	AL——概率向量，前向传播的输出（L_model_forward（））
	Y—真“标签”向量（非cat时包含0，cat时包含1）
	缓存--包含以下内容的缓存列表：
	每个带有“relu”的linear_activation_forward（）缓存（它是caches[l]，用于范围（l-1）中的l，即l=0…l-2）
	带有“sigmoid”的linear_activation_forward（）的缓存（它是caches[L-1]）
	返回：
	梯度词典
	grads[“dA”+str（l）]=...
	grads[“dW”+str（l）]=...
	grads[“db”+str（l）]=...
    """
    grads = {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
    
    # Initializing the backpropagation
    #(1 line of code)
    # dAL = ...
    # YOUR CODE STARTS HERE
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
    
    # YOUR CODE ENDS HERE
    
    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
    #(approx. 5 lines)
    # current_cache = ...
    # dA_prev_temp, dW_temp, db_temp = ...
    # grads["dA" + str(L-1)] = ...
    # grads["dW" + str(L)] = ...
    # grads["db" + str(L)] = ...
    # YOUR CODE STARTS HERE
    current_cache = caches[L-1]
    dA_prev_temp, dW_temp, db_temp = linear_activation_backward(dAL, current_cache, "sigmoid")
    grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = dA_prev_temp, dW_temp, db_temp
    # YOUR CODE ENDS HERE
    
    # Loop from l=L-2 to l=0
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        # Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)] 
        #(approx. 5 lines)
        # current_cache = ...
        # dA_prev_temp, dW_temp, db_temp = ...
        # grads["dA" + str(l)] = ...
        # grads["dW" + str(l + 1)] = ...
        # grads["db" + str(l + 1)] = ...
        # YOUR CODE STARTS HERE
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, "relu")
        grads["dA" + str(l)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
        
        # YOUR CODE ENDS HERE

    return grads

运行：

t_AL, t_Y_assess, t_caches = L_model_backward_test_case()
grads = L_model_backward(t_AL, t_Y_assess, t_caches)

print("dA0 = " + str(grads['dA0']))
print("dA1 = " + str(grads['dA1']))
print("dW1 = " + str(grads['dW1']))
print("dW2 = " + str(grads['dW2']))
print("db1 = " + str(grads['db1']))
print("db2 = " + str(grads['db2']))

L_model_backward_test(L_model_backward)

运行结果：

dA0 = [[ 0.          0.52257901]
 [ 0.         -0.3269206 ]
 [ 0.         -0.32070404]
 [ 0.         -0.74079187]]
dA1 = [[ 0.12913162 -0.44014127]
 [-0.14175655  0.48317296]
 [ 0.01663708 -0.05670698]]
dW1 = [[0.41010002 0.07807203 0.13798444 0.10502167]
 [0.         0.         0.         0.        ]
 [0.05283652 0.01005865 0.01777766 0.0135308 ]]
dW2 = [[-0.39202432 -0.13325855 -0.04601089]]
db1 = [[-0.22007063]
 [ 0.        ]
 [-0.02835349]]
db2 = [[0.15187861]]
 All tests passed.

6.4-更新参数

在本节中，将使用渐变下降更新模型的参数：
[]=[]− [] (16)
[]=[]− [] (17)
是学习率。
计算更新后的参数后，将其存储在参数字典中。

练习10-update_parameters

实现update_parameters（）以使用梯度下降更新参数。
说明：更新参数使用梯度下降对每一个[] 以及[] 为了=1,2,…, .

# GRADED FUNCTION: update_parameters

def update_parameters(params, grads, learning_rate):
    """
    使用梯度下降更新参数
	参数：
	params—包含参数的python字典
	grads——包含渐变的python字典，L_model_backward的输出
	return：
	参数——包含更新参数的python字典
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """
    parameters = params.copy()
    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    #(≈ 2 lines of code)
    for l in range(L):
        # parameters["W" + str(l+1)] = ...
        # parameters["b" + str(l+1)] = ...
        # YOUR CODE STARTS HERE
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
        
        # YOUR CODE ENDS HERE
    return parameters

运行：

t_parameters, grads = update_parameters_test_case()
t_parameters = update_parameters(t_parameters, grads, 0.1)

print ("W1 = "+ str(t_parameters["W1"]))
print ("b1 = "+ str(t_parameters["b1"]))
print ("W2 = "+ str(t_parameters["W2"]))
print ("b2 = "+ str(t_parameters["b2"]))

update_parameters_test(update_parameters)

运行结果：

W1 = [[-0.59562069 -0.09991781 -2.14584584  1.82662008]
 [-1.76569676 -0.80627147  0.51115557 -1.18258802]
 [-1.0535704  -0.86128581  0.68284052  2.20374577]]
b1 = [[-0.04659241]
 [-1.28888275]
 [ 0.53405496]]
W2 = [[-0.55569196  0.0354055   1.32964895]]
b2 = [[-0.84610769]]
 All tests passed.

祝贺你！
您刚刚实现了构建深层神经网络所需的所有功能，包括：
使用非线性单位可以改进模型
构建更深层次的神经网络（具有多个隐藏层）
实现一个易于使用的神经网络类
这确实是一项很长的任务，但任务的下一部分要容易些
在下一个作业中，您将把所有这些放在一起构建两个模型：
两层神经网络
L层神经网络
事实上，您将使用这些模型来分类猫与非猫的图像(喵！）干得好，下次见。