「SymPy」符号运算(4) 微积分与有限差分
目录
- 导言
- 积分
-
- 不定积分
- 定积分
- 多重积分
- 求导
-
- 一阶导数
- 高阶导数
- 偏导数
- 有限差分
-
- 常微分差分
- 差分系数
- 高阶差分
- 偏微分差分

导言
在前几篇中,我们学习了SymPy的基本语法、方程求解等基础知识
传送链接:
「SymPy」符号运算(1) 简介/符号/变量/函数/表达式/等式/不等式/运算符
「SymPy」符号运算(2) 各种形式输出、表达式的化简合并与展开
「SymPy」符号运算(3) (非)线性方程(组)求解、数列求和、连乘、求极限
这一节我们学习SymPy微积分的符号运算1,可以为科研工作中推导公式提供参考和验证。
注:本文只介绍标量的符号微积分,矢量和张量的符号微积分很快会出,请继续关注~
积分
不定积分
求符号积分,使用SymPy库中的integrate()函数,定积分与不定积分都是这个函数,不过仍进去的参数一个是纯符号、另一个是符号 + 积分上下界。
函数:integrate(f, var, ...) ,f是被积函数,var是符号 (不定积分)或符号 + 积分上下界(定积分)
不定积分就是求导数的原函数,将积分变量扔给函数的var参数。一个求不定积分的栗子: I = ∫ cos ( x ) d x I = \int \cos(x) \mathrm d x I=∫cos(x)dx
from sympy import symbols, integrate, cos
x = symbols('x')
I = integrate(cos(x), x)
I
输出:
sin ( x ) \sin(x) sin(x)
再举一个栗子: I = ∫ ( 3 x + 4 x 3 + 8 x 4 ) d x I = \int (3x + 4x^3 + 8x^4 )\mathrm d x I=∫(3x+4x3+8x4)dx
from sympy import symbols, integrate
x = symbols('x')
expr = 3*x + 4*x**3 + 8*x**4
I = integrate(expr, x)
I
输出:
8 x 5 5 + x 4 + 3 x 2 2 \frac{8 x^{5}}{5} + x^{4} + \frac{3 x^{2}}{2} 58x5+x4+23x2
可以注意到SymPy在求符号积分的时候是不会自动给出积分常数的。如果想要积分常数,需要自己手动添加,或者构造一个微分方程并用dsolve求解。
最后一个栗子: I = [ sin ( x ) + tan ( x ) ] d x I = [\sin(x) + \tan(x)]\mathrm d x I=[sin(x)+tan(x)]dx
import sympy
x = sympy.Symbol('x')
I = sympy.integrate(sympy.sin(x) * sympy.tan(x), x)
I
输出:
− log ( sin ( x ) − 1 ) 2 + log ( sin ( x ) + 1 ) 2 − sin ( x ) -\frac{\log{\left(\sin{\left(x \right)} - 1 \right)}}{2} + \frac{\log{\left(\sin{\left(x \right)} + 1 \right)}}{2} - \sin{\left(x \right)} −2log(sin(x)−1)+2log(sin(x)+1)−sin(x)
注意有一些函数求不出原函数,此时SymPy会给出一个Integral式子代替,如 I = ∫ x x d x I = \int x^x \mathrm dx I=∫xxdx
expr = integrate(x**x, x)
print(expr)
# Integral(x**x, x)
expr
输出:
∫ x x d x \int x ^x dx ∫xxdx
补充知识:我们自己也可以定义一个Integral对象,在能够求积时使用.doit()函数进行化简:
from sympy import Symbol, log, Integral
x = Symbol('x')
I = Integral(log(x)**2, x)
I
# Integral(log(x)**2, x)
I.doit()
# x*log(x)**2 - 2*x*log(x) + 2*x
定积分
定积分就是将integrate()函数第二个参数var换成(符号,积分下界,积分上界)
栗子: I = ∫ [ sin ( x ) cos ( x ) sin ( 2 x ) ] d x I = \int[\sin(x)\cos(x)\sin(2x)] \mathrm d x I=∫[sin(x)cos(x)sin(2x)]dx
from sympy import Symbol, sin, cos, pi, integrate
x = Symbol('x')
I = integrate(sin(x)*cos(x)*sin(2*x),(x,0,pi))
print(I)
# pi/4
栗子:求定积分 ∫ − ∞ ∞ x e − x 2 d x \int_{-\infty}^{\infty} x \mathrm e^{-x^2} \mathrm d x ∫−∞∞xe−x2dx
import numpy as np
import matplotlib.pyplot as plt
from sympy import init_session
init_session()
x = Symbol('x')
int_expr = integrate(x * exp(-x**2), (x, -oo, oo))
xcoord = np.linspace(-6, 6, 500)
ycoord = xcoord * np.exp(-xcoord ** 2)
plt.plot(xcoord, ycoord)
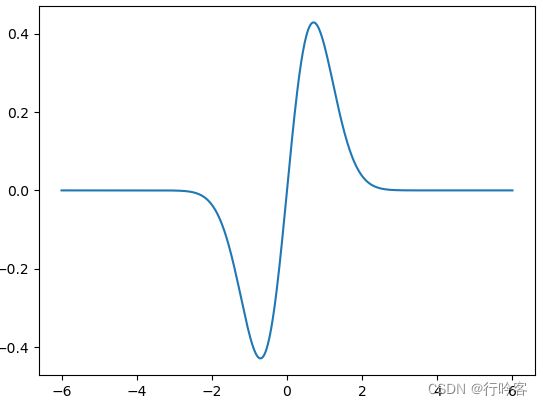
输出:0,简单地画一下 x e − x 2 x \mathrm e^{-x^2} xe−x2的图像:
多重积分
还是用integrate函数,几重积分就扔给函数几个符号(+上下界)
栗子:求 I = ∫ − ∞ ∞ ∫ − ∞ ∞ e − x 2 e − y 2 d x d y I = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2} e^{-y^2} \mathrm d x \mathrm dy I=∫−∞∞∫−∞∞e−x2e−y2dxdy
integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))
输出: π \pi π
求导
函数求导使用SymPy中的 diff函数:
diff(f, *symbols, **kwargs)
一阶导数
diff( ,如求 D = d d x ( x 3 ) D = \dfrac{\mathrm d }{\mathrm d x} (x^3) D=dxd(x3)
x = sympy.Symbol('x')
D = sympy.diff(x**3, x)
print(D)
# 3*x**2
高阶导数
sympy.diff( ,或者sympy.diff(
x = sympy.Symbol('x')
D = sympy.diff(x**3, x, 2)
print(D)
# 6*x
D = sympy.diff(x**3, x, x)
print(D)
# 6*x
以此类推,可以求n阶导数:diff(
偏导数
sympy.diff(
栗子:函数 f ( x , y , z ) = e x y z f(x, y, z) = \mathrm e^{xyz} f(x,y,z)=exyz,求 D = ∂ 7 f ∂ x ∂ y 2 ∂ z 4 D = \dfrac{\mathrm \partial^7 f}{\partial x \partial y^2 \partial z^4} D=∂x∂y2∂z4∂7f
from sympy import symbols, exp, diff
x, y, z= symbols('x y z')
f = exp(x*y*z)
diff(f, x, y, y, z, z, z, z)
# 或 diff(expr, x, y, 2, z, 4)
# 或 diff(expr, x, y, y, z, 4)
输出:
x 3 y 2 ( x 3 y 3 z 3 + 14 x 2 y 2 z 2 + 52 x y z + 48 ) e x y z x^{3} y^{2} \left(x^{3} y^{3} z^{3} + 14 x^{2} y^{2} z^{2} + 52 x y z + 48\right) e^{x y z} x3y2(x3y3z3+14x2y2z2+52xyz+48)exyz
补充知识:类似于SymPy的积分,如果遇到表达式不能求导,则diff函数会返回一个Derivative对象。自己也可以构造Derivative对象,并通过在合适的时候进行.doit()化简:
from sympy import Derivative
deriv = Derivative(f, x, y, y, z, 4)
deriv
输出:
∂ 7 ∂ z 4 ∂ y 2 ∂ x e x y z \frac{\partial^{7}}{\partial z^{4}\partial y^{2}\partial x} e^{x y z} ∂z4∂y2∂x∂7exyz
deriv.doit()
输出:
x 3 y 2 ( x 3 y 3 z 3 + 14 x 2 y 2 z 2 + 52 x y z + 48 ) e x y z x^{3} y^{2} \left(x^{3} y^{3} z^{3} + 14 x^{2} y^{2} z^{2} + 52 x y z + 48\right) e^{x y z} x3y2(x3y3z3+14x2y2z2+52xyz+48)exyz
有限差分
有限差分方法在数值计算领域中占据重要地位,是最经典、最简单、理论最完善的离散方法之一。SymPy提供了一些有限差分的相关计算方法。这里我们只介绍一个可以获得有限差分格式的函数:differentiate_finite()
differentiate_finite(expr, *symbols, points=1, x0=None, wrt=None, evaluate=False)
expr:被差分的表达式*symbols:被离散的自变量points:可以是- 序列:用来产生差分格式权系数的独立变量的离散点
- 值:就是步长,产生中心点 x 0 x_0 x0附近长度为差分阶数+1的等距序列的步长。缺省:步长为
1
x0:数字或者符号,差分近似的节点wrt:“with respect to”,在求偏导数的有限差分中,对哪个符号进行有限差分近似
常微分差分
设有两个函数 f ( x ) , g ( x ) f(x), g(x) f(x),g(x),获得 f ( x ) g ( x ) f(x)g(x) f(x)g(x)的有限差分:
from sympy import *
f, g = symbols('f g', cls=Function)
x = symbols('x')
# 默认的步长和离散的点数为 1 和 阶数+1
differentiate_finite(f(x)*g(x))
输出:
− f ( x − 1 2 ) g ( x − 1 2 ) + f ( x + 1 2 ) g ( x + 1 2 ) -f{\left(x - \frac{1}{2} \right)} g{\left(x - \frac{1}{2} \right)} + f{\left(x + \frac{1}{2} \right)} g{\left(x + \frac{1}{2} \right)} −f(x−21)g(x−21)+f(x+21)g(x+21)
获得 f ( x ) g ( x ) f(x)g(x) f(x)g(x)在指定点 x − h x-h x−h和 x + h x+h x+h的差分格式:
from sympy.abc import h
differentiate_finite(f(x)*g(x), x, points=[x-h, x+h])
输出:
− f ( − h + x ) g ( − h + x ) 2 h + f ( h + x ) g ( h + x ) 2 h -\frac{f{\left(- h + x \right)} g{\left(- h + x \right)}}{2 h} + \frac{f{\left(h + x \right)} g{\left(h + x \right)}}{2 h} −2hf(−h+x)g(−h+x)+2hf(h+x)g(h+x)
获得 f ( x ) g ( x ) f(x)g(x) f(x)g(x)在指定点 y y y, y + h y+h y+h和 y + 1.5 h y+1.5h y+1.5h的差分格式:
y = Symbol('y')
differentiate_finite(f(x)*g(x), x, points=[y, y+h, y+1.5*h], x0 = y)
输出:
− 1.66666666666667 f ( y ) g ( y ) h + 3.0 f ( h + y ) g ( h + y ) h − 1.33333333333333 f ( 1.5 h + y ) g ( 1.5 h + y ) h -\frac{1.66666666666667 f{\left(y \right)} g{\left(y \right)}}{h} + \frac{3.0 f{\left(h + y \right)} g{\left(h + y \right)}}{h} - \frac{1.33333333333333 f{\left(1.5 h + y \right)} g{\left(1.5 h + y \right)}}{h} −h1.66666666666667f(y)g(y)+h3.0f(h+y)g(h+y)−h1.33333333333333f(1.5h+y)g(1.5h+y)
差分系数
通过finite_diff_weights函数可以获得任意阶数的有限差分格式的系数:
finite_diff_weights(order, x_list, x0=1):
order:所需阶数,为0是就是插值x_list:差分所需的节点x0:差分的目标节点
from sympy import finite_diff_weights, S
res = finite_diff_weights(2, [-1, 0, 1], 0)
res
# [[[1, 0, 0], [0, 1, 0], [0, 1, 0]],
# [[0, 0, 0], [-1, 1, 0], [-1/2, 0, 1/2]],
# [[0, 0, 0], [0, 0, 0], [1, -2, 1]]]
res[0][-1] # 0阶差分的系数 [0, 1, 0]
res[1][-1] # 1阶差分的系数 [-1/2, 0, 1/2]
res[2][-1] # 2阶差分的系数 [1, -2, 1]
高阶差分
二阶差分,直接
dx = symbols('dx')
x0 = symbols('x0')
f = Function('f')
differentiate_finite(f(x), x, x, points = dx, x0 = x0)
# 等价于 differentiate_finite(f(x), x, 2, points = dx, x0 = x0)
输出:
− 2 f ( x 0 ) d x 2 + f ( − d x + x 0 ) d x 2 + f ( d x + x 0 ) d x 2 -\frac{2 f{\left(x_{0} \right)}}{dx^{2}} + \frac{f{\left(- dx + x_{0} \right)}}{dx^{2}} + \frac{f{\left(dx + x_{0} \right)}}{dx^{2}} −dx22f(x0)+dx2f(−dx+x0)+dx2f(dx+x0)
高阶差分以此类推。
偏微分差分
偏导数差分:
x, y = symbols('x y')
f = symbols('f', cls = Function)(x, y)
pf2pxpy = differentiate_finite(f, x, y, wrt=y)
pf2pxpy
输出:
− ∂ ∂ x f ( x , y − 1 2 ) + ∂ ∂ x f ( x , y + 1 2 ) -\frac{\partial}{\partial x} f{\left(x,y - \frac{1}{2} \right)} + \frac{\partial}{\partial x} f{\left(x,y + \frac{1}{2} \right)} −∂x∂f(x,y−21)+∂x∂f(x,y+21)
如果不使用参数wrt则会对针对每一个变量进行差分近似:
x, y = symbols('x y')
f = symbols('f', cls = Function)(x, y)
pf2pxpy = differentiate_finite(f, x, y)
pf2pxpy
输出:
f ( x − 1 2 , y − 1 2 ) − f ( x − 1 2 , y + 1 2 ) − f ( x + 1 2 , y − 1 2 ) + f ( x + 1 2 , y + 1 2 ) f{\left(x - \frac{1}{2},y - \frac{1}{2} \right)} - f{\left(x - \frac{1}{2},y + \frac{1}{2} \right)} - f{\left(x + \frac{1}{2},y - \frac{1}{2} \right)} + f{\left(x + \frac{1}{2},y + \frac{1}{2} \right)} f(x−21,y−21)−f(x−21,y+21)−f(x+21,y−21)+f(x+21,y+21)
Meurer A, Smith CP, Paprocki M, Čertík O, Kirpichev SB, Rocklin M, Kumar A, Ivanov S, Moore JK, Singh S, Rathnayake T, Vig S, Granger BE, Muller RP, Bonazzi F, Gupta H, Vats S, Johansson F, Pedregosa F, Curry MJ, Terrel AR, Roučka Š, Saboo A, Fernando I, Kulal S, Cimrman R, Scopatz A. (2017) SymPy: symbolic computing in Python. PeerJ Computer Science 3:e103 https://doi.org/10.7717/peerj-cs.103 ↩︎