并行计算随笔（一）

如果觉得本篇文章对你有所启发，请给我点个赞好吗，这对我很重要，谢谢

1 并行计算基础

1.1 什么是并行计算

1.1.1 对计算速度的需求

随着计算机硬件的快速发展，采用计算机进行大规模计算在科学研究中已经发挥越来越大的作用，逐渐成为科研人员和工程技术人员必不可少的研究手段和工具之一。随着数据规模的快速增大和求解问题复杂度的提高，仅仅靠单台计算机通常难以满足大规模快速计算的需要，尤其是对于天气预报、信息检索、新闻提炼这些时效性较高的应用，这些应用一般都属于我们说的巨大挑战性问题。对于老式的传统计算机来说，它们只有一个处理器（你可以简单理解为CPU）；而并行计算的出现，就是为了解决单台计算机算力不足的问题。所谓并行计算，就是指将一个应用分解为多个子任务，分配给不同的处理器，各个处理器之间相互协同，并行地执行子任务，从而达到提高求解速度，或者求解大规模应用问题的目的。这里我们要注意，多个处理器未必是多台计算机哦，随着时代的发展，一台计算机也拥有多个处理器。

1.1.2 并行计算

并行计算(Parallel Computing)在有些书上也叫平行计算；在后面的讲解中，我们的进程数或处理器数用p表示，而用多处理机(multiprocessor)来表示所有多于一个处理器的并行计算机系统。

1. 基本概念：并行计算是指在并行机上，将一个计算问题分解成多个子任务，分配给不同的处理器，各个处理器之间相互协同，并行地处理子任务，从而达到加速分解，或者求解大规模应用问题的目的。
2. 基本思想：通过多个处理器共同解决同一个计算问题，即每一个处理器单独承担整个计算任务中的一部分。
3. 目前问题：由于是不同处理器解决同一个计算问题，所以出现的问题就是如何分解计算问题。目前常见的方法大的来说分为时间上和空间上的并行。

1.1.3 并行计算的基本条件

1. 并行机；并行机需要包含多个处理器核心，这些处理器核心通过特定硬件相互连接，相互通信。
2. 应用问题必须具有并行度；也就是说，应用可以分解为多个子任务，这些子任务可以并行地执行。将一个应用分解为多个子任务地过程，成为并行算法地设计。
3. 并行编程。在并行机提供的并行编程环境上，具体实现并行算法，编制并行程序，并通过并行该程序，从而达到并行求解应用问题的目的。

下面通过一个数组求和的例子来给出并行算法设计的思路。虽然第一次见到这些公式可能会被吓到，但是这里我可以总结一下。

如果我们要解决一个$S={\sum }_{i=0}^{n-1}{a}_i$的问题。那我们实际上就是要求一个从0加到n-1的总数，那么我们可以设总数为n，其中这个n由四部分组成，即4个m，每两个m对应一台机器，也就是说，我们可以用下面的式子来表示我们上面说的：
$$S_0=\sum _{i=0}^{m-1}{a}_i,S_1=\sum _{i=m}^{2m-1}{a}_i,S_2=\sum _{i=2m}^{3m-1}{a}_i,S_3=\sum _{3m}^{n-1}{a}_i$$
这样的话，一个问题被分解成四部分计算。如果设$S_{00}=S_0+S_1$和$S_{01}=S_2+S_3$，可以同时计算$S_{00}$和$S_{01}$，最后再计算$S=S_{00}+S_{01}$。

1.1.4 平行计算和分布式计算

平行计算和分布式计算(distributed computing)都是用同一台电脑连接在一起，但是它们的目的不一样。并行计算是相对于串行计算而言的；分布式计算是相对于单机计算而言的。如果一个计算是串行跑的，即使他是在集群上跑的，也不是并行计算；同时，如果一个计算是在集群上跑的，即使是串行跑的，也是分布式计算。

并行计算（平行计算）	分布式计算
不同事件同时发生	跨系统或远程服务器的活动
将单个应用程序分散到多个核心/处理器/进程上，以更快的速度实现更大规模的应用	更多地关注并发性和资源共享
大多数用于科学计算	来自商业

并行和并发也是两个不一样的概念，关于这点，在计算机操作系统笔记中1.1.2.1并发中有记载，如果想了解可以去查看。

---

1.2 为什么需要并行计算

并行计算是人们为了提高求解问题的计算速度而提出的。根据摩尔定律，现在的电子元件已经做到了一个瓶颈了，如果想要提高计算效率，就必须从算法入手。所以即使单个计算机的计算能力已经非常强大，仍然无法满足有很多科学和工程计算问题的计算需求。因此，并行计算机是解决这些问题不可或缺的重要工具。

并行计算出现的根本原因是因为数据的积累。

举个例子，一个餐厅顾客很多，而且顾客还在源源不断地增加，如果想要更快地处理好这个问题，那肯定是增加服务员。同样地，高速公路地收费站；众所周知高速公路的车辆是非常多的，如果只有一个收费站，那就相当于串行，这样的话收费效率很慢，解决这类问题就是把公路拓宽，然后增加多个收费站同时收费。

---

1.3 并行计算机的发展

我国高性能计算机的研制水平一直处于世界领先行列，这对我国开展科学研究，促进技术进步，所起到的巨大推动作用是毋庸置疑的，然而我们必须清楚认识到，在使用高性能计算机方面，与先进国家相比，还有巨大差距。

---

1.4 并行算法复杂性分析

在数值计算中，我们通常需要预先知道一个算法在计算机上和何时能够完成。从理论上就可以得出哪些算法具有优势。因此，需要建立分析算法复杂性的手段，从而可以对算法进行定量评估。

那么，什么是算法复杂性呢？

算法复杂性主要是指由四则运算次数和存储空间大小两部分构成。为了能够更好地了解我们是怎么优化算法的，我们先来用两个例子看看算法的复杂性怎么算。

如果我们现在要计算$x^n$的复杂性，那么我们首先要给出计算$x^n$的算法，针对算法给出计算复杂性。诶，可能你说，我计算个$x^n$哪里需要那么复杂？比如$x^5$，我只需要先算，然后用$x^1$再乘一个$x^1$，然后依次计算完。但是也可以采取其他的顺序，比如先算$x_1$乘$x_1$。然后第三个$x_1$和第四个$x_1$相乘，这样得出两个$x_2$相乘后再乘上$x_1$。这就是我们算法的思想。据此我们也能看出，当所有$a_i$均非零时，这个算法的复杂性为2k+1。即$2lo{g}_{2}n+1$，这个就是我们说的算法复杂度了。不过在并行计算中，我们叫做计算复杂性。通过此算法可以看出，即使一个简单的问题，它的计算方法也可以很复杂。但该问题并不适合并行计算。

---

1.5 并行计算的基本概念

1.5.1 概念

粒度：在并行计算执行过程中，两个通信之间每个处理器计算工作量大小的粗略描述，分为细粒度和粗粒度。

粒度在并行算法设计中必不可少，通常在进程数与效率之间选择粒度的大小，比如后面将要介绍的MPI并行程序更适合粗粒度并行，而使用CUDA并行程序就需要细粒度。

并行度：某一时刻多个处理器上可以同时执行的子任务个数。

并行度越高，说明可以使用的处理器多，但不一定有好的效率，需要根据具体问题具体分析。

加速比（在一些书上也被叫做加速系数）：求解一个问题的最佳串行算法执行时间与并行算法地执行时间之比。

在一个多处理机上研发求解时，也许最感兴趣的一个问题是：采用多处理机求解该问题能快多少？为了进行这种比较，我们应该使用单处理器能得到的最优解（也就是上面提到的最佳串行算法执行时间）与在多处理机上所研究的并行算法进行比较。加速比是对相对性能的衡量，它的定义为：$S(p)=\frac{使用单处理器系统执行时间}{使用具有p个处理器的多处理机的执行所需的时间}$

如果我们用$T_s$来表示分子部分，用$Tp(q)$来表示分母部分，那么公式可以简化为：$S(p)=\frac{T_s}{Tp(q)}$。

S§给出了使用多处理机后所能得到的速度增加。

在理论分析中，加速系数也可以根据计算步来进行预测，即：

$S(p)=\frac{使用单处理器所需的计算步数}{使用具有p个处理器所需的并行计算步数}$

对于顺序计算，通常用时间复杂性来比较不同的算法。也就是说，我们对于并行计算也可以同样应用时间复杂性来比较，也就是计算步数。但是我们忽略的是，在并行计算中，我们不仅仅考虑算法本身的优劣，实际应用中还要考虑各并行部分之间的联系所需的开销。

效率：有时需要知道处理器在多长时间内用于有用的计算，这可以从（系统）效率(efficiency)推得。至此我们可得定义：

$E=\frac{使用单处理器的执行时间}{使用多处理机执行时间\times 处理器个数}=\frac{T_s}{T_{p(q)}\times P}=\frac{S(p)}{p}$

其中E以百分比形式表示，例如，如果E有百分之五十，则平均来讲，处理器仅有一半的时间是用来计算的。百分之百的最大效率仅当所有处理器在所有时间都用于计算时才会出现。

1.5.2 最大加速比

那么谈论了这么多，到底是什么原因限制了加速呢？

• 有时并非所有处理器都能完成有用的工作，从而导致了一些处理器处于闲置状态。
• 在并行版本中需要在顺序计算中不会出现的额外计算。例如对常数重新进行局部计算。
• 进程间的相互通信。

---

1.6 并行计算机分类

一台并行计算机可以是一台具有多个内部处理器的单计算机，也可以是多个互联的计算机构成一个一体的高性能计算平台。术语并行计算机通常是指专门设计的部件。根据不同的分类法可以分成不同类型的并行计算机。

1.6.1 费林分类法

在操作系统中我们知道，程序根据高级程序设计语言设计，程序设计语言在实现程序的功能的时候，是转换为机器指令来告诉机器该干什么。大概在50年前Flynn(1996)创造了一种计算机分类方法,中文译为费林分类法，该分类基于两个独立维度的计算机体系结构，这两个维度即数据和指令。

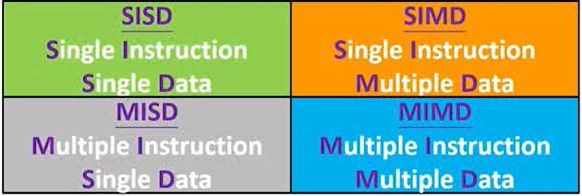
根据以上提到这两个维度，我们可以划分为四大类，如图：

1.6.1.1 SISD

Single Instruction,Single Data(SISD)

SISD机器是一种传统的串行计算机，它的硬件不支持任何形式的并行计算，所有的指令都是串行执行。并且在某个时钟周期（时间片）内，CPU只能处理一个数据流。因此这种机器被称作单指令流单数据流计算机。早期的计算机都是SISD机器，如冯诺.依曼架构，如IBM PC机，早期的巨型机和许多8位的家用机等。

1.6.1.2 MIMD

Multiple Instruction,Multiple Data(MIMD)

在一个通用的多处理机系统中，每个处理器拥有一个独立的程序，由每个程序为每个处理器生成一个指令流，不同的数据可能需要不同的处理，对应赋给不同的指令。每条指令对不同数据进行操作。Flynn将这种形式的计算机分类为多指令流多数据流计算机。

我们前面叙述的共享存储器或消息传递多处理机都属于MIMD类型。其已经经受了时间考验，至今仍然广泛地用于这种操作模式下的计算机系统中。例如多核CPU计算机。

1.6.1.3 SIMD

Single Instruction,Multiple Data(SIMD)

如果对某些应用而言将计算机设计成由单一程序生成指令流，但是却有多个数据存在时，将会在性能上有很大的优势。打个比方，你输入一条指令就能够处理很多的数据，那不就是提高了性能吗。我们熟知的Hadoop就是基于SIMD的。

SIMD是采用一个指令流处理多个数据流。这类机器在数字信号处理、图像处理、以及多媒体信息处理等领域非常有效。

Intel处理器实现的MMXTM、SSE（Streaming SIMD Extensions）、SSE2及SSE3扩展指令集，都能在单个时钟周期内处理多个数据单元。也就是说我们现在用的单核计算机基本上都属于SIMD机器。

1.6.1.4 MISD

Multiple Instruction,Single Data(MISD)

MISD是采用多个指令流来处理单个数据流。由于实际情况中，采用多指令流处理多数据流才是更有效的方法，谁会去一个数据多个指令去处理呀。因此MISD只是作为理论模型出现，仅仅只在1971年CMU的实验中出现过，也就是说，实际上并不存在SISD。

---

1.6.2 存储器结构分类法

1.6.2.1 共享存储器多处理机

这里说得比较晦涩难懂，实际上，这里和操作系统进程的共享存储是同一回事，详情可见计算机操作系统笔记2.1.4.2 共享存储。

再说的简洁点，这里指的共享存储器多处理机你完全可以理解为一个多核的计算机或者很多个单核的共用一份内存的计算机。

也就是说，处理器如果想要处理数据，那么就得跑去存储器拿数据。怎么知道数据在哪呢？通过存储器上的地址去拿。

在操作系统中我们学过，如果这个时候两个处理器要同时在一个存储器上拿东西，那它们一定要提前沟通好，也就是说，两个处理器对共享空间的访问是互斥的。它们提前沟通的工具是互联网络。

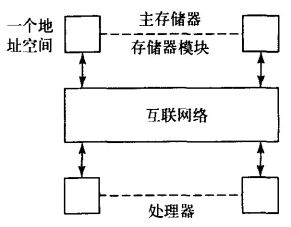
多处理机系统由多台独立的处理机组成，每台处理机都能够独立执行自己的程序和指令流，相互之间通过专门的网络连接，实现数据的交换和通信，共同完成某项大的计算或处理任务。系统中的各台处理机由统一的操作系统进行管理，实现指令级以上并行，这种并行性一般是建立在程序段的基础上，也就是说，多处理机的并行是作业或任务级的并行。共享存储多处理机系统是指有一个可以被所有处理机访问的存储器系统。存储器系统由一个或多个存储器模块组成，所有的存储器模块使用一个统一的编址的地址空间。处理机可以用不同的地址访问不同的存储器模块。按存储器组织方式分类，共享存储多处理机系统分为集中式共享存储器系统和分布式共享存储器系统。

对共享存储器多处理机进行编程设计到在共享存储器中存有可由每个处理器执行的代码。每个程序所需的数据也将存于共享存储器中。（即程序段和数据段都在共享内存中）。因此如果有需要的话，每个程序可以访问所有的数据。

程序员要想使用并行计算机的每个处理器来处理一件问题，那原有的高级程序语言就无法使用了。所以为了解决此问题，程序员们开发了一种新的、高级并行程序设计语言，它具有特殊的并行程序设计构造和语句，以声明共享变量和并行代码段。虽然想法很好，但是这类并行程序设计语言并不是使用很广泛。

比较广泛的做法是在普通的高级程序语言的基础上生成并行代码，你可以理解为嵌入式编码（类似于嵌入式SQL）。此时使用制定好规则的编程语言，然后用预处理器命令对程序的并行部分加以说明即可；这类实践比较著名的模型就是OpenMP。它去油编译器命令和构造的一个工业标准，可融入到C/C++中。

另外，我们也可以多开几条线程，这样的话给人的感觉也像是并行计算的样子，不同线程中含有为各个处理器执行的规整的高级语言代码序列，这些代码序列可以用来访问共享单元。但是需要注意的是，实际上用线程的方法不是并行而是并发。

使用一个规则的顺序编程语言，并修改语法以说明并行性。这也是一种常用的共享存储器多处理机模型，常用的模型是UPC（即统一并行C，Unified Parallel C）。

共享存储器多处理机是很一种很不错的并行计算机，综上所述，其方便了对数据的共享。

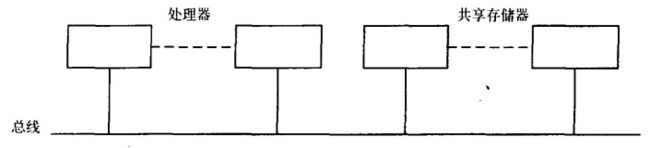
对于上图所示的基于总线互联结构的小型共享存储器多处理机系统是很流行的。这种在很多系统中都有广泛应用。但是用硬件来达到所有处理器的快速访问是很困难的，特别是在有大量存储器时。因此大多数大型的共享存储器系统具有某种形式的层次或分布式存储器结构，以此来使得处理器能够更快的速度访问物理上相近的处理单元。

1.6.2.2 消息传递多计算机

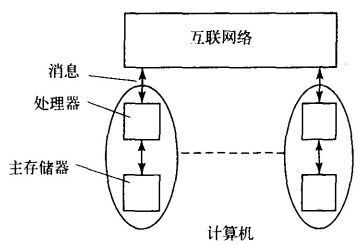
另外一种多处理机系统的形式可以通过互联网络连接多台完整的计算机来构成。这里实际上对应了操作系统笔记中2.1.4.4 消息传递。

多处理机系统的形式可以通过互联网络连接多台完整的计算机来构成。如下图所示：

每台计算机由一个处理器和本地主存储器组成，其他处理器不可访问该本地的主存储器。换句话来讲，就是一台计算机的处理器只能访问它对应本地的主存储器，而无法访问其他计算机上的主存储器。不同的计算机之间是用互联网来建立联系的，通常来说，多个电脑之间通过互联网传递的消息含有的可能是程序所指明的其他计算机处理器进行计算时所需的数据。这种多处理器系统我们通常称为消息传递多处理机(message-passing multiprocessor)，或简称多计算机。你可以理解为多计算机实质上是真正意义上的分布式存储器计算机（不是分布式共享存储器哈）。

我们在操作系统常提到进程这个概念，在多计算机上，我们可以把一个问题分成多个并发进程，它们可在各台计算机上分别执行。如果有6个进程和6个计算机，则我们可在每台计算机上执行一个进程；如果进程数大于计算机数，那么其中一台计算机中如果是多核可以采用并行执行，如果是单核可以采用分时方式执行。进程间将通过发送消息的原语来联系对方。同样地，发送消息可以采用两种方式，一种是直接通信方式，一种是间接通信方式，如果想详细了解，可以前往教材或者操作系统笔记中了解。

消息传递多计算机比共享存储器多处理机更容易在物理上进行扩展，也就是说它可以构成较大规模。一般规模比较小的叫做机群（Cluster），规模比较大的叫做超级计算机（SuperComputer），规模很大的叫做数据中心（DataCenter）。

1.6.2.3 分布式共享存储器

对于程序员来说，消息传递多计算机并没有像共享存储器多处理机那么好用，因为它通常需要程序员在它们的代码中使用显式的消息传递调用，即用原语来进行数据交换。而这又非常容易出错，且很难调试，所以在程序中写的代码很类似于低级的汇编语言。（你想想是不是嘛？你要写代码去调硬件，那不就是汇编嘛。）数据不能共享且必须拷贝，在一些具体的应用中这就很可能成为问题，因为要拷贝，数据冗余不说，还要多次拷贝，多次操作。但是消息传递多处理还是有很多优点的：它不需要专门的同步机制以控制对数据的同时访问。如果使用这些机制，将会明显提高并行程序的执行时间。

由于意识到从编程观点而言期望使用共享存储器范例，一些研究人员开始追求分布式共享存储器系统的概念。从名字上面看，存储器物理地分布在每个处理器中，但每个处理器使用单一的存储器地址空间对整个存储器进行访问。当一个处理器要访问的单元不在本地存储器中时，必须使用消息传递方法在处理器和存储单元之间以某种自动方式进行数据的传递，以隐藏存储器是分布的这一事实。当然，远程访问将导致更大的延迟，而且比起本地访问来，此延迟常常是相当大的。

简单来说就是，分布式共享存储器的内存在物理上分离，逻辑上统一。

1.6.2.4 共享存储器多处理机体系结构

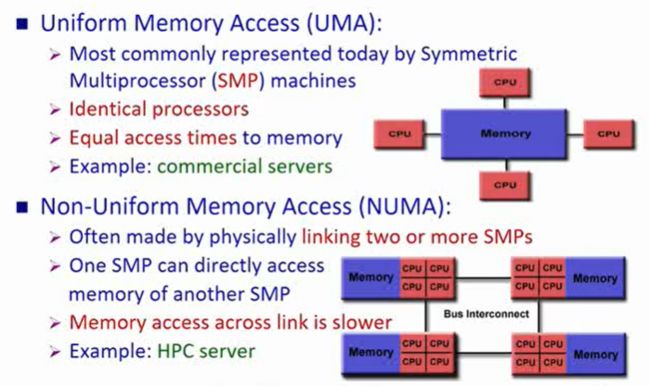
根据1.6.2.1 讲述的共享存储器多处理机结构，我们还能按存储器组织方式分类，共享存储多处理机系统分为集中式共享存储器系统（Unirom Memory Access，UMA）和分布式共享存储器系统（Non-Unirom Memory Access，NUMA）。

集中式共享存储器系统由于直接访问存储器，所以拥有高效率，并且每个处理器到达存储器的时间都相等。但是当CPU太多，很可能不能一起连在同一个存储器上，而且效能可能也会达到某个程度上不去。例如commercial servers(商用服务器)。

而分布式共享存储器系统不能直接访问存储器，其跨连接的访问存储器速度较慢，但是其CPU的增多提高了计算效率；在CPU增多提高的效率大于访问存储器时间效率损失时，我们也可以理解为是一种高效。例如HPC server(高效能服务器)。

---

1.7 并行计算模型

并行编程模型作为硬件或内存架构之上的抽象存在。一般来说，编程模型的设计与计算机体系结构相匹配。如：

• 如果是共享内存程序，那么对应共享内存机模型
• 如果是消息传递程序，那么对应分布式内存机模型（消息传递模型）

虽然，一般来说是上面两种模型，但是其并不是一一对应。编程模型不受机器或内存体系结构的限制。即使你是一台电脑，也可以使用分布式内存机模型，即使你是多台电脑，也可以使用共享内存模型。

1.7.1 共享内存模型

对于共享内存模型来说，最著名的两个模型莫过于Pthread和OpenMP。对于Pthread来说，它是并行源代码调用的子程序库，也就是说写起来相对复杂，抽象度比较低。而对于OpenMP来说，抽象度比较高，这就意味着我们并不需要写过多的代码。其为嵌入在串行或并行源代码中的一组编译器指令。如图所示：

1.7.2 消息传递模型

消息传递模型可以在计算过程中使用自己的本地内存的一组任务。多个任务可以驻留在同一台物理机器上和/或跨任意数量的机器。任务通过发送和接收消息，通过通信交换数据。这和我们操作系统里面讲到的消息传递所做的事是一样的，只是这里写的比较抽象。

消息传递模型建立在MPI（消息传递接口）上，其常见的API为：send 、recv、 bcast、Gather、Scatter等。

1.7.3 两种模型的优缺点

共享内存模型

优点	缺点
可以分享数据结构	没有区域性控制
只需注释循环	规模不大
解决串行代码

消息传递模型

优点	缺点
区域性控制	需要重新思考整个应用/数据结构问题
CPM通信在代码中都是显式的	有些问题不知道什么时候说“接收”
	大量繁琐的打包/解包代码

---

1.8 机群计算

1.8.1 以互联计算机作为计算平台

综上所述，我们已经讲了许多专门设计、用作并行计算平台的并行计算机，其中包括多处理机和多计算机。

实际上多年来，许多大学的研究项目都偏向于去研究多处理机系统。但是问题是，在你研究的时候，处理器不断的在更新迭代，也就是说第二年的处理器速度很可能比第一年的处理器速度快一倍。那后面n年后买的处理器说不定是第一年处理器效率的n倍。

为了解决上述问题，超级计算机的开发商只有一种办法：我不是说后面n年后买的处理器说不定是第一年处理器效率的n倍吗？那我就买n个处理器，用钱来解决一切。当然，这样对钱不友好。

在后期，一些大学尝试了一种更为经济的办法，就是不用多处理机啦，用多计算机，即使用互联的工作站和PC机来构成一个强大的计算平台。使用工作站网络有许多显著优点胜过那些专门设计的多处理机系统，关键的优点如下：

• 可用较低的成本使用有很高性能的工作站和PC机
• 系统可以很容易地引入那些可以买到的最新的处理器，且系统可以通过加入附加的计算机磁盘以及其他资源增量式地加以扩展自身原有的硬件
• 可使用已有的应用软件或对之加以修改

为了让这些很多计算机连接起来的计算机网络（并行计算机）去设计并行程序，在后期又发明了并行虚拟机（Parallel Virtual Machine，PVM）。在后面出现了消息传递多计算机后， 又定义了标准的消息传递库，即消息传递接口MPI（Message-Passing Interface）。

而在后续的历史中，PC机越来越便宜，使得工作站的概念和PC机两者的区别已经消失。现在我们采用的小型并行计算机，叫做机群(clusster)，这个我们在1.6.2.2 已经提到过了。而我们用机群去解决一个问题的过程，我们称为机群计算（cluster computing）。

1.8.2 超级计算机的概念

在前面我们已经提到过超级计算机了，即中规模计算机群。超级计算机一般用机柜装着，单位用U（unit，单元）来表示，一般来说超级计算机的机柜是16-42U，一个服务器一般是1-4U。

有时候一个机柜很大，不一定服务器就能放的很多，一般服务器放的多少取决于其散热，如果使用水冷散热的话，一个机柜放的服务器数量就能增加。

这里还需要引入一个知识：

CUP核数即一个CPU由多少个核心组成,核心数越多,代表这个CPU的运转速度越快,性能越好。对于同一个数据处理,一核CPU相当于1个人处理数据,双核CPU相当于2个人处理同一个数据,4核CPU相当于4个人去处理同一个数据,因此处理核心数越多,CPU的工作效率也就越高。

一般来说，现在的CPU上面一般有4-12个核心，而为了加速计算速度，后面又出现了GPU。

所以一般我们给超级计算机的定义如下：

超级计算机：与通用计算机相比，具有高级计算能力的计算机

一般来说，衡量一个超级计算机的好坏是用其每秒能计算几个浮点数来衡量的，而用来检验浮点数的多少是用HPL Benchmark（即高性能计算机基准）来检验的。

高性能计算机基准实际上是在计算一个线性矩阵方程，每秒算出来的浮点数的多少即为衡量超级计算机好坏的标准。当然，超级计算机性能并不是越大越好，符合自己计算要求即可，不需要太高，过高性能的超级计算机价格也高，烧钱。

综上所述，组成一台超级计算机需要考虑很多方面，主要方面如下：

• 硬件设施的来源
• 自定义系统配置
• 优化的软件和库
• 巨大的金钱和能源成本

超级计算机实际上也是衡量一个国家的军事实力的标准。

1.8.3 并行计算机系统互连

1.8.3.1 以太网连接

联网计算机的通信方法通常使用的是以太网类型。最初的以太网由单条总线（简称单线）构成，所有的计算机都连接在该总线上。而现在单线被各种交换器和集线器所代替，但以太网的协议不变。

交换器可以理解为计算机网络中的每个点，不同的总线汇集的点用交换器连着。集线器也是如此

源和目标结点之间的所有传递都是按包的形式进行传递的。如果一个数据过大，那么就要分割成多个包分别传输，等到到了目的地再将所有的包重组成为完整的数据 。

需要注意的是，最初使用单条总线时，线只有一条但是有多个计算机，这就导致了要是同时有计算机发出信息包会对总线做一个抢占，如果一个计算机发出了信息包，那么另外一个检测到单线有消息包他就不会发出消息包。

最初的以太网速度很慢，直到光纤的诞生速度才慢慢上来，但是实际上，以太网的消息传递时延仍然很大。

1.8.3.2 TCP/IP

TCP/IP是一个标准，它构成了联网计算机进行通信和传递数据的规则。也就是说，联网计算机不同于前面的以太网连接的计算机，根据TCP/IP联网的计算机每个主机上都有一个地址，一般来说都是形如：192.168.1.1。

1.8.4 并行程序间的通信——网络拓扑

1.8.4.1 基本概念

相比于多处理器计算机，多计算机是需要互连的，而通过什么来连接是至关重要的，我们不一定要采用网络来进行传输，也可以用最朴素的方式——一根总线。而对于连接各台计算机来说，无非就是考虑几点要素：高效能、成本（cost）、可扩展性（scalabilety）、带宽（bandwidth）、时延（latency）。

时延和带宽是计算机网络的知识，这里简要说明下。

“带宽”原本指某个信号具有的频带宽度，即最高频率和最低频率之差，单位是赫兹（Hz）。而在计算机网络中，带宽用来表示网络的通信线路传送数据的能力，通常是指单位时间内从网络中的某一点到另外一点所能通过的最高数据率。单位是“比特每秒”。

而对于时延来说，一般大的看分为三类：

时延种类	说明
网络时延	一般指的是消息经过网络传输时所需的时间
通信时延	是指发送消息所需的总时间，包括软件开销和接口延迟
消息时延	消息时延也被叫做启动时间，也就是发送消息时所需的软硬件开销，还必须加上沿互联通路发送数据所需的确切传送时间。

而按过程来看也可以如下分类：

发送时延（传输时延）	从发送分组的第一个比特算起，到该分组的最后一个比特发送完毕所需的时间，其为主机把数据放到信道上的过程。	$发送时延=\frac{数据长度}{信道带宽（发送速率）}$
传播时延	取决于电磁波传播速度和链路长度。	$传播时延=\frac{信道长度}{电磁波在信道上的传播速率}$
排队时延	等待输出/入、链路可用
处理时延	检错、找出口

两个结点之间路径的物理链路数也是一个重要的考虑元素，因为它是确定消息延时的主要因素。其中术语网络直径是网络内两个相距最远的结点的最小链路数。网络直径给定了单个消息必须经历的最大距离，它可为某些并行算法找到通信的下限。

1.8.4.2 拓扑结构

如果谈到拓扑结构，那么就要从最简单的开始说起，也就是我们再1.8.3.1 提到的最简单的单线结构，单线结构简单，但是对于时延和可恢复性较差，一旦一条线路间有一处地方断裂，那整条网路就断了。

为了解决此问题循环结构出现了，也就是对于单条总线多加一条总线。这样的话，如果想要切断整个网络，需要切断两条线，虽然听着可恢复性还是很差，但是是单线结构的两倍可恢复性，是一个较大的进步了。

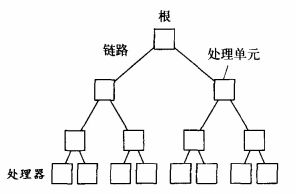
后来又出现了树状结构，其使用的是二叉树。

对于上图的树状网来说，树中的每个交换器都有两条链路与位于其下层的2个结点相连，这种结构我们叫做完全二叉树。而树状网也可以是非完全二叉树。树状结构的时延很低，但是可恢复性也很差。

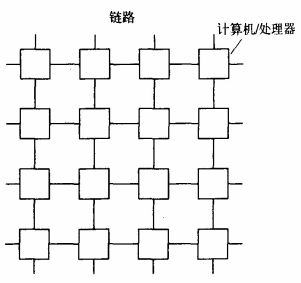
比较广泛使用的有限互联网络应该是网络（2D-Mesh）和超立方体（hypercube）。网络的网络拓扑如下：

如果在每个自由端结点与其对立端结点循环相连，则就构成了环绕网。这种网格结构不易断裂，扩展性能好，时延也低。

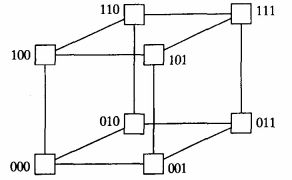
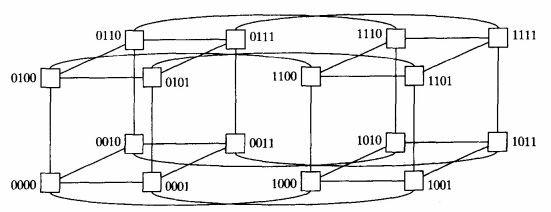
超立方体网络也有分类，一种是3D超立方体，一种是4D超立方体。如下所示：

需要注意的是，超立方体的开销高和可扩展性差，一个node要如此多的链路连接，成本肯定先对要高。

除了上面说的网络拓扑，还有一些网络拓扑如：纵横交差交换器、多级互联网等。

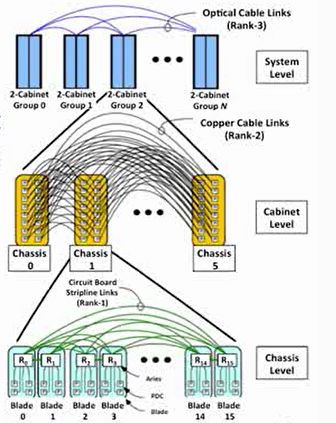
还有一种蜻蜓拓扑，其利用高基数路由器、长通道光纤的技术进步，现在被最新的超级计算机所使用。