水平集图像分割并行加速算法设计与实现(串行、OpenMP、CUDA)——OpenMP并行实现篇
本次水平集图像分割并行加速算法设计与实现包含：原理篇、串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇四个部分。
原理篇主要讲解水平集图像分割的原理与背景。串行实现篇、OpenMP并行实现篇与CUDA GPU并行实现篇主要基于C++与OpenCV实现相应的图像分割与并行加速任务。本系列属于图像处理与并行程序设计结合类文章，希望对你有帮助。
PCAM设计与分析
根据陈国良院士在《并行算法实践》中的讲解，一般而言，并行程序的设计过程可以划分为4步：即任务划分(Partitioning)、通信(Communication)分析、任务组合(Agglomeration)和处理器映射(Mapping)，简称为PCAM设计过程，具体如下图所示。
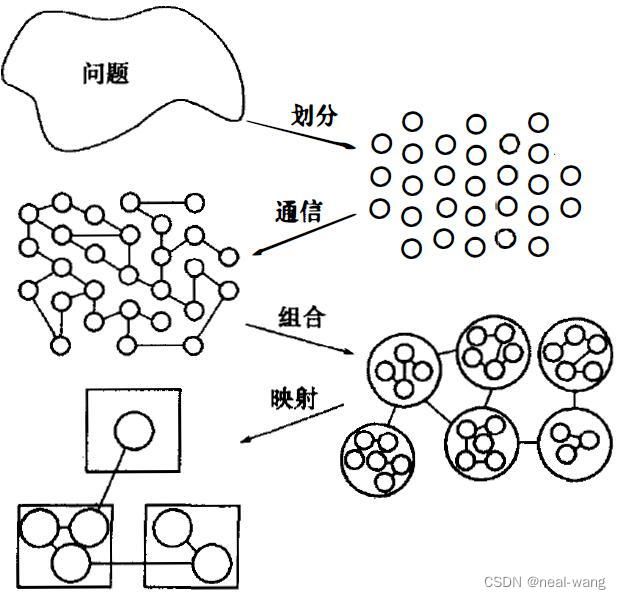
这四个阶段可以简述为如下：
- 划分：将整个计算分解为一些小的任务，其目的是尽量开拓并行执行的机会；
- 通信：确定诸任务执行中所需交换的数据和协调诸任务的执行，由此可检测上述划分的合理性；
- 组合：按性能要求和实现的代价来考察前两阶段的结果，必要时可将一些小的任务组合成更大的任务，以提高性能或减少通信开销；
- 映射：将每个任务分配到一个处理器上，其目的是最小化全局执行时间和通信成本以及最大化处理器的利用率。
本文后续将从上述四个阶段角度对所设计的OpenMP并行程序进行分析。
并行流程设计
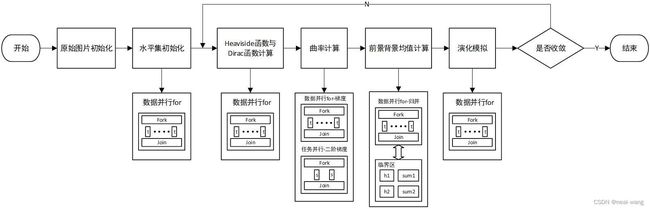
本次OpenMP水平集图像分割并行加速算法的设计流程如上图所示。其分别在水平集初始化模块、Heaviside函数与Dirac函数计算以及演化模拟等模块进行数据并行；在曲率计算模块采用数据并行与任务并行结合的方式；在前景背景均值计算模块由于存在相应归并操作，在数据并行的同时需要设定临界区保护，具体主要模块的PCAM分析与实现如下节所示。
主要并行模块PCAM分析与实现
水平集初始化并行模块
针对该模块的PCAM分析如下：
- 划分：将图像处理任务按图像行进行划分，每N（进程数/图像高度）个行为一组。
- 通信：各组仅需处理自身数据，无需通信。
- 组合：各组不需要组合。
- 映射：将各组映射到不同的处理器或进程，利用OpenMP库实现各组的并行计算。
在该模块的具体实现方面，其主要采用#pragma omp for语句，运用数据并行对初始化代码中的循环语句进行并行化，具体代码如下所示：
// 初始化水平集
void LevelSet::initializePhi(cv::Point2f center, float radius)
{
const float c = 2.0f;
#pragma omp parallel shared(c)
{
float value = 0.0;
#pragma omp for
for (int i = 0; i < src_.rows; i++)
{
for (int j = 0; j < src_.cols; j++)
{
value = -sqrt(pow((j - center.x), 2) + pow((i - center.y), 2)) + radius;
if (abs(value) < 1e-3)
{
//在零水平集曲线上
phi_.at<float>(i, j) = 0;
}
else
{
// 在零水平集内：为正
// 在零水平集外：为负
phi_.at<float>(i, j) = value;
}
}
}
}
}
曲率计算并行化模块
根据曲率计算逻辑，可将该模块分为一阶梯度及其模值的计算与二阶梯度计算两个部分。
针对一阶梯度及其模值的计算部分进行PCAM分析如下：
- 划分：将图像处理任务按图像行进行划分，每N（进程数/图像高度或一阶梯度图像）个行为一组。
- 通信：各组仅需处理自身数据，无需通信。
- 组合：各组不需要组合。
- 映射：将各组映射到不同的处理器或进程，利用OpenMP库实现各组的并行计算。
针对二阶梯度计算部分进行PCAM分析如下：
- 划分：将任务划分为求解x方向的二阶梯度（dxx）与求解y方向的二阶梯度(dyy)两部分。
- 通信：各组仅需处理自身数据，无需通信。
- 组合：各组不需要组合。
- 映射：将各组映射到不同的处理器或进程，利用OpenMP库实现各组的并行计算。
在具体代码实现的过程中，针对一阶梯度及其模值相关计算部分运用#pragma omp for语句，采用数据并行进行并行化。而针对二阶梯度计算，由于要分别对x方向与y方向的二阶梯度进行计算，运用#pragma omp sections语句，采用任务并行模式进行并行化。具体代码如下所示：
// 计算曲率
void LevelSet::calculateCurvature()
{
Mat dx, dy;
gradient(src_, dx, dy);
Mat norm = Mat::zeros(src_.size(), CV_32FC1);
Mat dxx, dxy, dyx, dyy;
#pragma omp parallel shared(dx,dy,norm,dxx, dxy, dyx, dyy)
{
#pragma omp for
for (int i = 0; i < src_.rows; i++)
{
for (int j = 0; j < src_.cols; j++)
{
norm.at<float>(i, j) = pow(dx.at<float>(i, j) * dx.at<float>(i, j) + dy.at<float>(i, j) * dy.at<float>(i, j), 0.5);
}
}
#pragma omp sections
{
#pragma omp section
{
gradient(dx / norm, dxx, dxy);
}
#pragma omp section
{
gradient(dy / norm, dyx, dyy);
}
}
}
curv_ = dxx + dyy;
}
前景背景均值计算并行化模块
针对前景背景均值计算模块进行PCAM分析如下：
- 划分：将图像处理任务按图像行进行划分，每N（进程数/图像高度）个行为一组。
- 通信：由于在该模块中存在全局归并操作，需要对全局临界区的使用进行相应通信。
- 组合：各组不需要组合。
- 映射：将各组映射到不同的处理器或进程，利用OpenMP库实现各组的并行计算。
在该模块的具体代码实现中采用#pragma omp for语句进行数据并行。且由于其存在归并操作，需要对前景与背景像素总值和像素总个数进行统计，故在本次个人实验中运用#pragma omp critical语句进行相应的临界区保护，具体代码如下所示：
// 计算像素点前景与背景均值
void LevelSet::calculatC()
{
c1_ = 0.0f;
c2_ = 0.0f;
float sum1 = 0.0f;
float h1 = 0.0f;
float sum2 = 0.0f;
float h2 = 0.0f;
#pragma omp parallel shared(sum1,sum2,h1,h2)
{
float h = 0.0f;
float value = 0.0f;
#pragma omp for
for (int i = 0; i < src_.rows; i++)
{
for (int j = 0; j < src_.cols; j++)
{
value = src_.at<float>(i, j);
h = heaviside_.at<float>(i, j);
#pragma omp critical
{
h1 += h;
sum1 += h * value;
h2 += (1 - h);
sum2 += (1 - h) * value;
}
}
}
}
c1_ = forntpro_ * sum1 / (h1 + 1e-10);
c2_ = sum2 / (h2 + 1e-10);
}
演化模拟并行模块
针对演化模拟模块的PCAM分析如下：
- 划分：将整个演化模拟任务按图像行进行划分，每N（进程数/图像高度）个行为一组。
- 通信：各组仅需处理自身数据，无需通信。
- 组合：各组不需要组合。
- 映射：将各组映射到不同的处理器或进程，利用OpenMP库实现各组的并行计算。
在该模块的具体实现过程中，运用#pragma omp for语句对循环进行数据并行操作，具体代码如下所示：
// 具体演化函数
// 运用迭代法解偏微分方程，求解φ对应时间间隔的变化量
int LevelSet::evolving()
{
showEvolving();
showLevelsetEvolving();
// 迭代次数
int k;
bool flag; //是否收敛判定标识
for (k = 0; k < iterationnum_; k++)
{
flag = false;
heaviside();
dirac();
calculateCurvature();
calculatC();
#pragma omp parallel shared(flag)
{
#pragma omp for
// 模拟演化过程
for (int i = 0; i < src_.rows; i++)
{
for (int j = 0; j < src_.cols; j++)
{
float curv = curv_.at<float>(i, j);
float dirac = dirac_.at<float>(i, j);
float u0 = src_.at<float>(i, j);
float lengthTerm = mu_ * dirac * curv;
float areamterm = nu_ * dirac;
float fittingterm = dirac * (-lambda1_ * pow(u0 - c1_, 2) + lambda2_ * pow(u0 - c2_, 2));
float term = lengthTerm + areamterm + fittingterm;
float phinew = phi_.at<float>(i, j) + timestep_ * term;
float phiold = phi_.at<float>(i, j);
phi_.at<float>(i, j) = phinew;
if (!flag)
{
if (phinew * phiold < 0)
{
flag = true;
}
}
}
}
}
showEvolving();
showLevelsetEvolving();
// 对是否收敛进行判断
if (!flag)
{
break;
}
}
showEvolving();
showLevelsetEvolving();
return k;
}
上述代码中的虽存在对共享存储flag的操作，但其仅可以令flag为true，不存在进程间共享内存的篡改问题，且一旦flag为true时，代码最后的收敛性判定部分将锁定，不再允许进程进入。
由于篇幅所限，文内仅仅展现部分主要代码，详细代码见本人github仓库所示，具体链接如下 。
水平集图像分割算法串行与并行代码以及相关测试用例
测试用例
本次并行加速算法的测试用例主要分为实体测试用例与性能测试用例两部分，下面将分别对两部分测试用例进行介绍。
实体测试用例
实体测试用例主要来源于实际生活中存在，或虚拟应用场景中存在的图形图像。针对实际存在实物方面，选取人脸嘴唇图片作为测试用例，其尺寸为883像素*594像素，具体如下图所示。
针对虚拟业务场景方面，本次个人实验选取两张飞机游戏图片作为测试用例，其中飞机游戏图片一尺寸为320像素*570像素，飞机游戏图片二尺寸为476像素*752像素，具体如下所示。
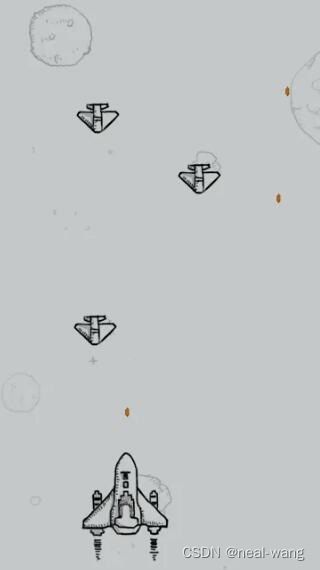
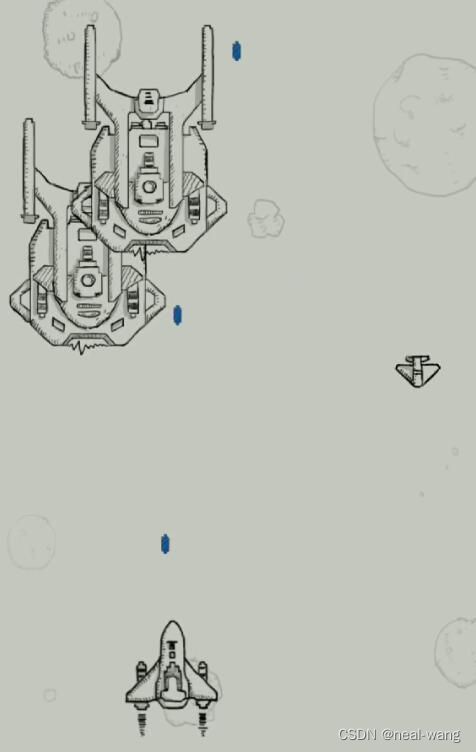
性能测试用例
性能测试用例主要通过随机生成的图形进行构建，其包含有尺寸从1000像素*1000像素到8000像素*8000像素的8张图片，以此来对并行算法针对不同数据量的处理性能进行测试，具体图片示例如下图所示。
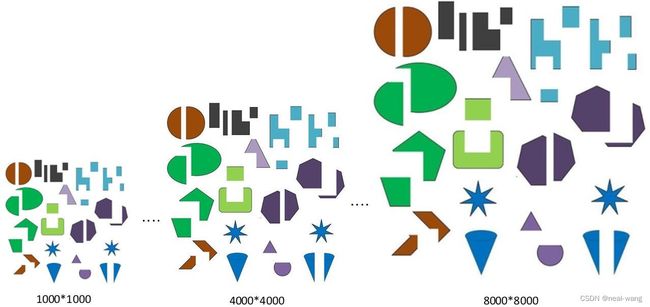
运行环境说明
硬件运行环境
CPU：Intel® Core™ i5-9300H 4核CPU处理器
GPU：NVIDIA GeForce GTX 1050显卡
软件运行环境
OpenCV: v4.5.0
运行结果与性能测试
如下设置线程数为8进行全部测试。
实体测试用例结果与性能分析
针对人脸嘴唇图片，OpenMP并行程序以时间步长为1进行测试，最大迭代次数为1000，得到的测试结果如下图所示。
针对飞机游戏图片一，OpenMP并行程序以时间步长为5进行测试，最大迭代次数为1000，得到的测试结果如下图所示。
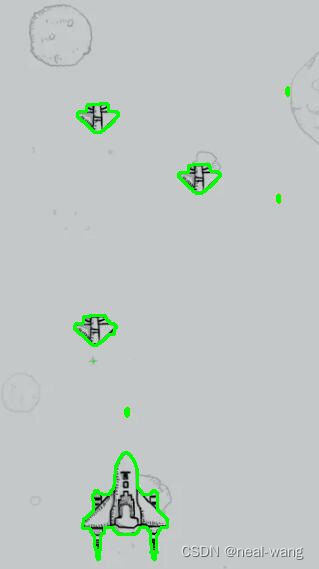
针对飞机游戏图片二，OpenMP并行程序以时间步长为5进行测试，最大迭代次数为1000，得到的测试结果如下图所示。
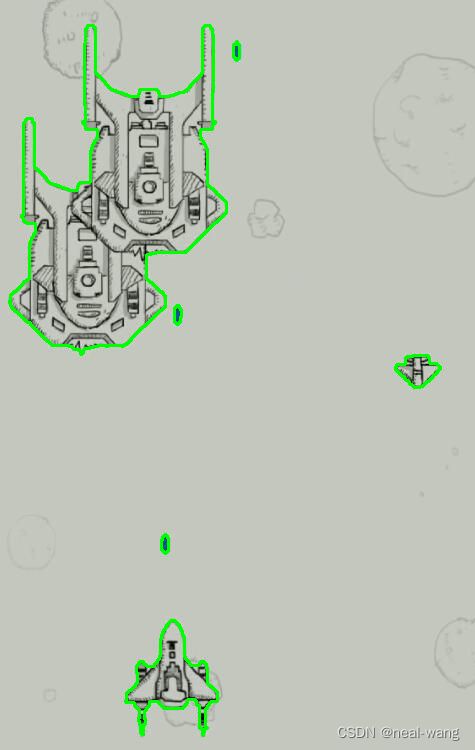
经过对比验证上述三张图片与串行程序运行结果一致，详细水平集图像分割串行程序设计与实现见本系列串行实现篇。
针对上述实体测试用例进行性能分析，分别取各图片十次运行时间进行平均，得到实体测试用例OpenMP并行时间表，同时可计算其相对于串行程序的加速比，具体如下表所示：
| 图片名称 | 人脸嘴唇 | 飞机游戏一 | 飞机游戏二 |
|---|---|---|---|
| 时间(ms) | 253104 | 24564 | 160518 |
| 加速比 | 1.351847462 | 1.414671878 | 1.370712319 |
具体针对实体测试用例的串行程序与OpenMP并行程序运行时间对比图如下所示。
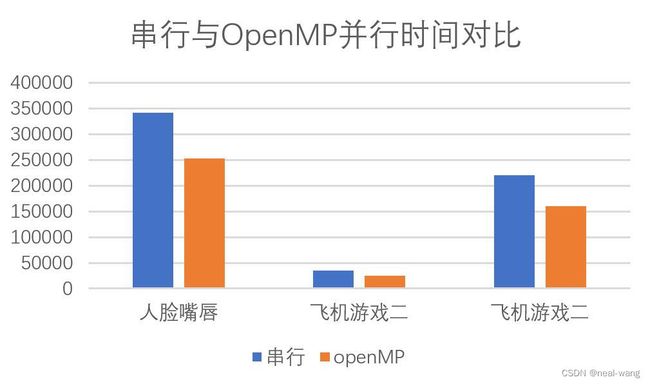从上图与OpenMP并行时间表中可看出，OpenMP并行程序相比于串行程序，在实体测试用例上，整体运行效率得到了显著的提升。
性能测试用例结果与性能分析
针对性能测试用例，运用步长为100进行测试，最大迭代次数为100，所得到的测试结果如下图所示。
针对上述性能测试用例进行性能分析，分别取各图片十次运行时间进行平均，得到性能测试用例OpenMP并行时间表，同时可计算其相对于串行程序的加速比，具体如下表所示：
| 测试图像大小 | 时间(ms) | 加速比 |
|---|---|---|
| 1000 | 71477 | 1.651832 |
| 2000 | 246464 | 1.727676 |
| 3000 | 501621 | 1.829704 |
| 4000 | 981626 | 1.865899 |
| 5000 | 1598811 | 1.884471 |
| 6000 | 2151669 | 1.931734 |
| 7000 | 2974506 | 1.956799 |
| 8000 | 3852300 | 2.022704 |
由于本次项目运用4核处理器进行OpenMP测试，当图片大小达到8000像素*8000像素时，加速比可以达到二以上，加速效果显著，具体针对性能测试用例的串行程序与OpenMP并行程序运行时间对比图如下所示。
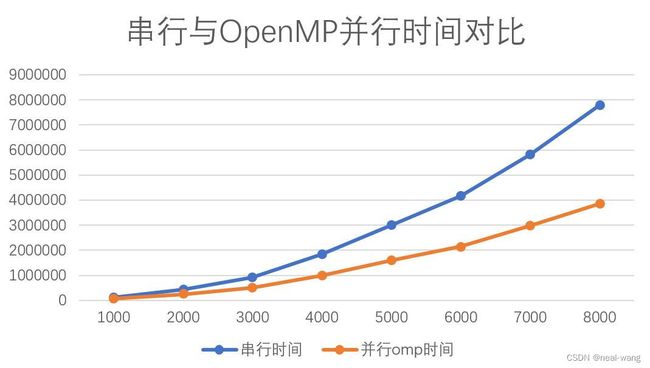
从上图中也可以看出，随着测试图像的不断增大，串行程序运行时间增加迅速，而OpenMP程序运行时间增速明显放缓。当图像大小为8000*8000时，OpenMP程序可以节省一半运行时间。
下期将对水平集图像分割CUDA并行加速算法的设计与实现进行详细介绍，欢迎关注！