基本的图算法
基本的图算法主要是两个方面:图的表示和图的搜索。我们主要通过邻接链表和邻接矩阵对图进行表示,但是在图算法更重要的是图的搜索,图的搜索指的是系统化的跟随图中的边来访问图中的每个节点,我们可以通过图的搜索算法发现图的结构。或者换个方面想图的算法就是通过图的搜索得到图的结构,所以图的算法就是对基本的搜索加以优化,因此图的搜索技巧是整个图算法的核心。
图的表示
对于一个图,我们有两种标准表示方法表示。一种表示法将图作为邻接链表的组合,另一种表示法则将图作为邻接矩阵来看待,两种方法既可以表示有向图也可以表示无向图。
两种方法的主要区别在于,邻接链表在表示系稀疏图时非常紧凑而成为通常的选择,但是在稠密图的情况下,我们更倾向于使用邻接矩阵表示法,此外如果要快速判断任意两个节点之间是否有边相连,使用邻接矩阵表示法更方便。
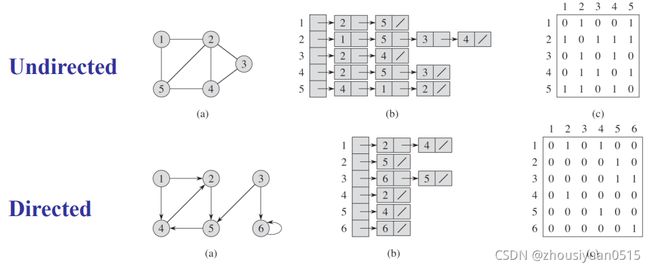
由上图我们就能清晰的看到邻接矩阵与邻接链表的结构,临界矩阵通过建立点的个数个链表储存图的结构,每条链表代表与其相连的节点,而邻接矩阵就更浅显易懂了,通过01的表示储存两个节点间是否存在联系,我们更直接的能看到,对于无向图邻接矩阵是一个对称矩阵,而有向图则不然。图上我们看到,对于邻接链表所需的存储空间为(V+E),而对于邻接矩阵,我们需要V^2的空间存储矩阵。
如果要表示权重图,对于邻接链表,我们需要将权值存储在邻接链表中即可,而对于邻接矩阵,我们将权重存放于对应位置即可,不存在的边存储为NIL。
对图的多数算法需要维持图中结点或边的某种属性,我们在邻接链表需要使用额外的数组来表示节点属性。
广度优先搜索(BFS)
广度优先搜索时最简单的图搜索算法之一,也是许多重要的图算法的模型。给定一个源节点s,广度优先搜索可以发现从源节点s能够到达的所有节点,算法能够计算出到每个节点的最短距离,同时生成一棵广度优先搜索树。
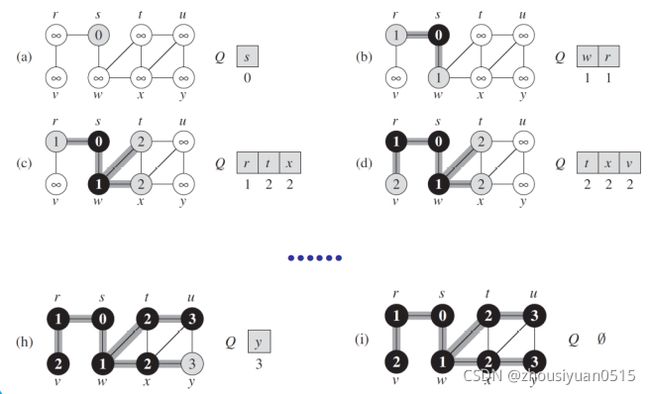
广度优先搜索始终将已发现的节点与未发现节点的边界,沿其广度方向向外拓展,简而言之就是搜索的时候首先发现距离源节点为k的节点,再发现距离为(k + 1)的节点。
所以我们在搜索过程中就是建立一个搜索树的过程,最开始只有根节点,在向下发现节点时,每发现一个就将其加入树中,按照对于边(u , v)节点u为v的父节点,对于每个节点,他至多被发现一次,最多只有一个父节点。我们将未被发现的节点记为白色,处在发现队列中的点记为灰色,与其邻接的节点都被发现的节点记为黑色。
从伪代码我们不难看出除了搜索的过程和树的建立,我们还需要一个优先队列先进先出管理刚被发现尚未检索完毕的节点。分析其运行时间可得,总时间为O(V + E).
这段BFS是从某道做过的题里扒出来的,将就着看把大伙。
void BFS(int i, int j,int n,int m) {
queue que; //定义队列
Node tep_node;
tep_node.x = i,tep_node.y = j;
que.push(tep_node); //入队
inque[i][j] = true; //标记已经入队
while(!que.empty()) { //队列非空
Node top = que.front(); //取出队首元素
que.pop(); //队首元素出队
/*for(int i = 0; i < 4; ++i) { //访问相邻的四个元素
int tepi = top.x;
int tepj = top.y;
int nowI = top.x + X[i];
int nowJ = top.y + Y[i];
if(judge(nowI,nowJ,tepi,tepj,m,n)) {
node.x = nowI,node.y = nowJ;
que.push(node); //入队
inque[nowI][nowJ] = true;//标记已经入队
count++;
}*/
}
}
if(count > tep)tep = count;
count = 1;
} 深度优先搜索
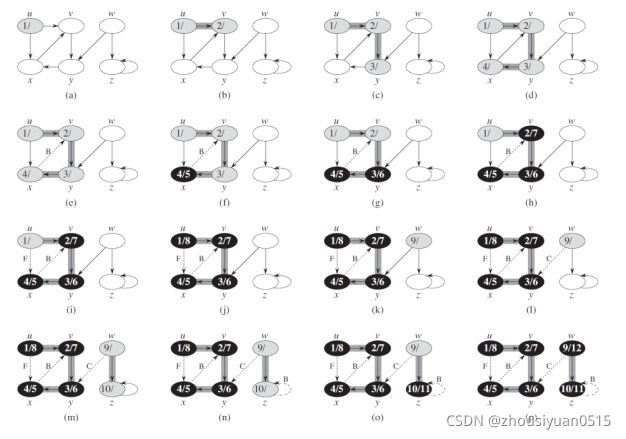
深度优先搜索就像名字所说的,只要可能,就在图中尽量深入。深度优先搜索(DFS)总是对刚出现的节点的出发边进行搜索,直到所有出发边都被发现为止。同时,一旦所有出发边都被发现,那么搜索就回溯到节点的前驱节点,来搜索前驱节点的出发边。搜索将一直持续直到可以到达的节点都被发现,如果存在未被发现的节点,则取出一个节点作为新的源节点并重复上述过程,直至所有节点都被发现。
与上文所说BFS不同,广度优先搜索的前驱子图形成一棵树,而深度优先搜索的子图是由多棵树组成,因为搜索可能从多个源节点重复进行。因此广度优先搜索的过程将创建一颗广度优先树,深度优先搜索形成的是一个由多个深度优先树构成的深度森林。而且值得注意的是,每个节点仅在一颗深度优先树中出现,即所有深度优先树不相交。
此外,深度优先树要在节点上盖上时间戳:第一次被发现的时间和最后一次被发现的时间(涂灰和涂黑的时间)。
下面是伪代码:
由伪代码可知,深度优先搜索的运行时间为o(V+E).
同理这个也是从题里面扒出来的。
int dfs(int p = s, int cur_flow = INF){
if (p == t) return cur_flow;
long long ret = 0;
for (int i = cur[p]; i != 0; i = edges[i].next){
cur[p] = i;
long long v = edges[i].to, vol = edges[i].weight;
if (level[v] == level[p] + 1 && vol > 0){
int f = dfs(v, min(cur_flow - ret, vol));
edges[i].weight -= f;
edges[i^1].weight += f;
ret += f;
if (ret == cur_flow) return ret;
}
}
return ret;
}拓扑排序
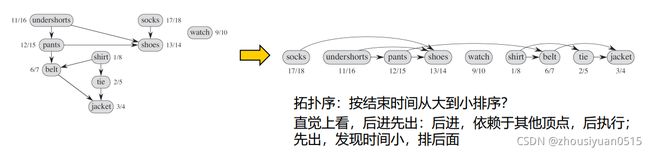
拓扑排序是对图G中所有节点的一次线性排序,次序满足如下条件:如果图G包含边(u,v),则节点u在拓扑排序中处于节点v的前面(如果有环路,则无法排序),因此可以将一个图的拓扑排序看作是将图的所有结点在一条水平线上排开,图的所有有向边都从左指向右。借用老师的图就是这样的:
拓扑排序很简单伪代码就三行,懒得放了,直接放点代码把。
这段代码写的是最大拓扑排序,先说拓扑排序应该怎么做吧。拓扑排序就是每次找入度为0的点进入优先队列,然后出队并把他的边去掉,再次进行循环,最后排成一列。
而最大拓扑排序写的是一个动态过程(就是黑心助教改题),每次找到一个入度为0的节点入队后,马上更新找下一个最大的入度为零的节点,因此就是一个动态的过程,相当于每次循环我们只做两件事,第一件事是找出最大的入度为零的点,第二件事是把与这个节点有关的边全都抹去,循环判断条件就是优先队列里没元素了就停止(是不是听起来很简单,就是很简单)。你问我为什么不放拓扑排序的代码,因为懒不想改了。
#include
using namespace std;
const int maxn = 4e5 + 5;
int head[maxn];
int ind[maxn];// 记录入度
int ans[maxn];//记录答案
int cnt;
int n, m;
struct EdgeNode{
int to;
int w;
int next;
};
EdgeNode edge[maxn];
void init(){
cnt = 0;
memset(ans, 0, sizeof(ans));
memset(head, -1, sizeof(head));
memset(ind, 0, sizeof(ind));
}
void top(){
priority_queue, less > Q;
for(int i = 1; i <= n; i++){
if(!ind[i]){
Q.push(i);
}
}
int num;
while(!Q.empty()){
num = Q.top();
ans[cnt++] = num;
Q.pop();
for(int i = head[num]; i != -1; i = edge[i].next){
int v = edge[i].to;
ind[v]--;
if(ind[v] == 0)
Q.push(v);
}
}
for(int i = 0; i < cnt; i++)
{
if(i)
printf(" ");
printf("%d",ans[i]);
}
printf("\n");
}
int main(){
cin >> n >> m;
init();
for(int i = 1 ; i <= m; i ++){
int a,b;
cin >> a >> b;
edge[i].to = b;
edge[i].next = head[a];
head[a] = i;
ind[b] ++;
}
top();
} 链式前向星
刚开始上手一脸懵逼,上手了之后都说好的东西。想了半天怎么解释,还是算了直接上代码。(聪明的人一看就知道我把上面的拓扑排序放的代码截了两段过来)
#include
using namespace std;
const int maxn = 4e5 + 5;
int head[maxn];
int ind[maxn];// 记录入度
int ans[maxn];//记录答案
int cnt;
int n, m;
struct EdgeNode{
int to;
int w;
int next;
};
EdgeNode edge[maxn];
int main(){
cin >> n >> m;
init();
for(int i = 1 ; i <= m; i ++){
int a,b;
cin >> a >> b;
edge[i].to = b;
edge[i].next = head[a];
head[a] = i;
ind[b]++;
}
} 说实话,就是链表本来是动态的,现在变成静态的罢了,存图可能更形而上学一点,解释一下各个变量含义,to是终点,w是边权,next是与这个边起点相同的上一条边的编号,同时也看到了定义的head数组,head[i]表示以i为起点的最后一条边的编号,这样就把整个图串成一串了。
5 7
1 2 1
2 3 2
3 4 3
1 3 4
4 1 5
1 5 6
4 5 7
output:
1 //以1为起点的边的集合
1 5 6
1 3 4
1 2 1
2 //以2为起点的边的集合
2 3 2
3 //以3为起点的边的集合
3 4 3
4 //以4为起点的边的集合
4 5 7
4 1 5
5 //以5为起点的边不存在输入进来的过程:
对于1 2 1这条边:edge[0].to = 2; edge[0].next = -1; head[1] = 0;
对于2 3 2这条边:edge[1].to = 3; edge[1].next = -1; head[2] = 1;
对于3 4 3这条边:edge[2].to = 4; edge[2],next = -1; head[3] = 2;
对于1 3 4这条边:edge[3].to = 3; edge[3].next = 0; head[1] = 3;
对于4 1 5这条边:edge[4].to = 1; edge[4].next = -1; head[4] = 4;
对于1 5 6这条边:edge[5].to = 5; edge[5].next = 3; head[1] = 5;
对于4 5 7这条边:edge[6].to = 5; edge[6].next = 4; head[4] = 6;
遍历函数
for(int i = 1; i <= n; i++)//n个起点
{
cout << i << endl;
for(int j = head[i]; j != -1; j = edge[j].next)//遍历以i为起点的边
{
cout << i << " " << edge[j].to << " " << edge[j].w << endl;
}
cout << endl;
}累了,后面的图算法可能得等更久才能憋出来了。