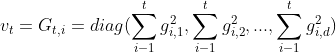机器学习11种优化器推导过程详解(SGD,BGD,MBGD,Momentum,NAG,Adagrad,Adadelta,RMSprop,Adam,Nadma,Adamx)
前言
在网上看了很多关于优化函数的讲解，基本都是从两本书完全照抄搬运到知乎和CSDN等各大技术论坛，而且搬运的过程中错误很多：一本是李沐的《动手学深度学习》，另一本是邱锡鹏的《神经网络与深度学习》，这里从新总结和修正一下。
在神经网络的训练中，有两个重要的概念，一个是损失函数，一个是优化函数，简单来说损失函数是评价指标，优化函数是网络的优化策略，常用的优化函数有 SGD、BGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam、Nadam、Adamax等 其中：
- SGD、BGD、MBGD 三个算法都是使用梯度下降算法对网络权重进行更新，只是每次更新使用的样本数量不同。（ SGD属于离线学习，BGD、MBGD属于在线学习）
- Momentum和NAG算法是根据局部历史梯度对当前梯度进行平滑。
- Adagrad，Adadelta，RMSprop算法都是自适应学习率的优化算法，对于不同参数使用不同的自适应学习率；Adagrad使用梯度平方和、Adadelta，RMSprop使用梯度一阶指数平滑（一阶指数平均，局部加权历史梯度）解决了Adagrad后期梯度非常小的问题；RMSprop是Adadelta的一种特殊形式。
- Adam算法吸收了Momentum和RMSprop算法的优点，同时改进了梯度计算方式和学习率，本质上是带有动量项的RMSprop。
- Nadam，Adamax是对Adam的进一步优化
深度学习优化算法经历了 BGD -> SGD -> MBGD -> SGDM -> NAG ->AdaGrad -> AdaDelta/RMSprop -> Adam -> AdaMax -> Nadam 这样的发展历程，本文简单来梳理这些优化算法是如何一步一步演变而来的。
0、基本参数概念
梯度下降是指，在给定待优化的模型参数θ和损失函数J(θ)后，算法通过沿梯度ΔJ(θ)的相反方向更新θ来最小化J(θ)。学习率η决定了每一时刻的更新步长。对于每一个时刻t，我们可以用下述步骤描述梯度下降的流程：
计算目标函数关于当前参数的梯度，对J(θ)求导：
根据历史梯度计算一阶动量和二阶动量：
计算当前时刻的下降梯度：
根据下降梯度进行更新参数：
最核心的区别就是第三步所执行的下降方向，在这个式子中，前半部分是实际的学习率（也即下降步长），后半部分是实际的下降方向。不同优化算法也就是不断地在这两部分上做文章。
1、梯度下降
1.1. SGD（Stochastic Gradient Descent 随机梯度下降）
SGD随机梯度下降参数更新原则：单条数据就可对参数进行一次更新。每个epoch参数更新M（样本数）次，这里的随机是指每次选取哪个样本是随机的，每个epoch样本更新的顺序是随机的
- 优点：参数更新速度快。
- 缺点：由于每次参数更新时采用的数据量很小，造成梯度更新时震荡幅度大，容易受到异常值的影响，在最优解附近会有加大波动，但大多数情况都是向着梯度减小的方向。
注：离线学习就是使用随机梯度下降算法对模型进行更新，对于每一个样本都计算一次梯度并更新模型
1.2. BGD（Batch Gradient Descent 批量梯度下降）
BGD批量梯度下降参数更新原则：每次将所有样本的梯度求和，然后根据梯度和对参数进行更新，每个epoch参数更新1次。
- 优点：由于每次参数更新时采用的数据量很大，梯度更新时很平滑。
- 缺点：由于每次参数更新时采用的数据量很大，造成参数更新速度慢，内存消耗大，因为梯度更新平滑随机性差，容易陷入局部最优解。
1.3. MBGD（Mini-Batch Gradient Descent 小批量梯度下降）
MBGD小批量梯度下降参数更新原则：只用所有数据的一部分进行参数的每一次更新。本质上就是在每个batch内部使用BGD策略，在batch外部使用SGD策略。
1. 减少了参数更新的变化，这可以带来更加稳定的收敛。2：可以充分利用矩阵优化，最终计算更加高效。
- 优点：相比于SGD，由于每次参数更新时采用的数据量相对较大，梯度更新时相对平滑；相比于BGD，由于每次参数更新时采用的数据量相对较小，参数更新速度相对较快。
- 缺点：没有考虑数据集的稀疏度和模型的训练时间对参数更新的影响。
注：MBGD优化器对每个batch内所有样本的梯度求均值，然后使用梯度的均值更新模型，因此使用MBGD优化器进行更新属于离线学习，同理BGD也属于离线学习
2、动量（一阶动量）
2.1. Momentum（动量梯度下降）
Momentum梯度下降算法在与原有梯度下降算法的基础上，引入了动量的概念，使网络参数更新时的方向会受到前一次梯度方向的影响，换句话说，每次梯度更新都会带有前几次梯度方向的惯性，使梯度的变化更加平滑，这一点上类似一阶马尔科夫假设；Momentum梯度下降算法能够在一定程度上减小权重优化过程中的震荡问题。
引入动量的具体方式是：通过计算梯度的指数加权平均数来积累之前的动量，进而替代真正的梯度，Momentum的优化函数的权重更新公式如下：
通过上述公式可以在，动量参数
本质上就是到目前为止所有历史梯度值的加权平均，加上当前梯度
乘以学习率η，距离越远的梯度，权重越小，η常取0.9。
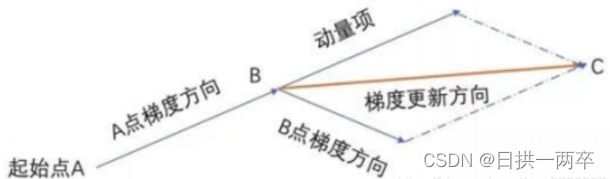
如下图，B点更新梯度时不是沿着原有的梯度方向，而是结合动量项产生的新梯度方向BC更新。
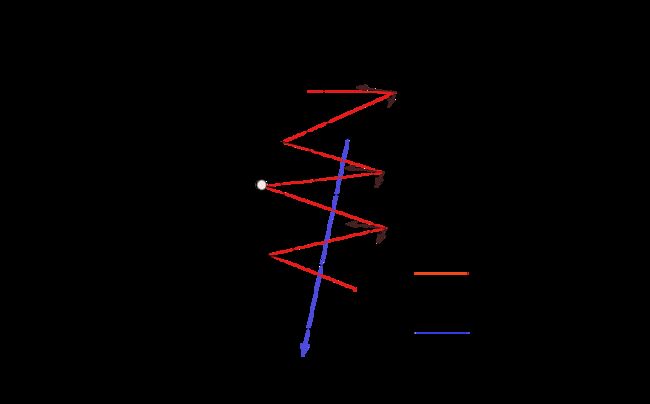
通过下面这张图片来理解动量法如何在优化过程中减少震荡
上图中每次权重更新的方向可以分解成W1方向上的w1分量和w2方向上的w2分量，红线是传统的梯度下降算法权重更新的路径，在w1方向上会有较大的震荡；
如果使用动量梯度下降算法，算法每次会累计之前的梯度的值。以A点为例，在A点的动量是A点之前所有点的梯度的加权平均和，这样会很大程度抵消A点在w1上的分量，使A点在w2方向上获得较大的分量，从而使A点沿蓝色路径（理想路径）进行权重更新。
- 优点：加入的这一项，可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。
- 缺点：这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要到坡底时，就知道需要减速了的话，适应性会更好。
2.2.SGD with Momentum
为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些。SGDM全称是SGD with momentum，在SGD基础上引入了一阶动量：
梯度更新规则:
Momentum在梯度下降的过程中加入了惯性，使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。
一阶动量是移动平均值，这里 β 的经验值为0.9，也就是说时刻t的主要下降方向是由t-1时刻的下降方向再加一点点t时刻的偏向决定的。
存在问题:
- 不具备一些先知，例如快要上坡时，就知道需要减速了，适应性会更好；
- 不能根据参数的重要性而对不同的参数进行不同程度的更新。
2.3. NAG（Nesterov Accelerated Gradient 牛顿动量梯度下降）
Nesterov Accelerated Gradient （牛顿动量梯度下降） 算法是Momentum算法的改进，原始公式如下：
更新损失函数J(θ)的参数θ，β代表衰减率，η代表学习率：
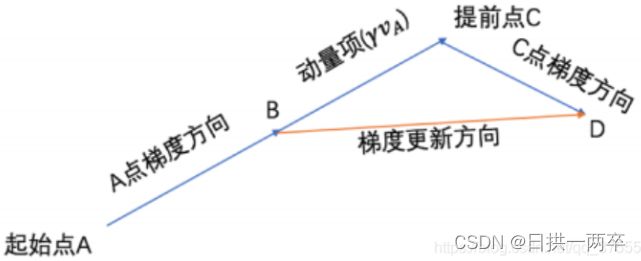
参考下图理解：当从A点走到B点时，分别求出了动量项
和提前点C点的梯度
，从而得出B点的梯度更新方向BD。好处是如果在C点发生了梯度反向反转，则B点可以提前获取到这个信息，修正B的梯度更新值BD，减少收敛过程中的震荡。若C点梯度方向不变，则会在下一次梯度方向上产生加速效果。可与前文Momentum优化方法的区别进行对比。
如果说Momentum算法是用一阶指数平滑，那么NGA算法则是使用了二阶指数平滑；Momentum算法类似用已得到的前一个梯度数据对当前梯度进行修正（类似一阶马尔科夫假设），NGA算法类似用已得到的前两个梯度对当前梯度进行修正（类似二阶马尔科夫假设），无疑后者得到的梯度更加准确，因此提高了算法的优化速度。
- 应用：NAG 可以使 RNN 在很多任务上有更好的表现。
- 缺点：不能根据参数的重要性而对不同的参数进行不同程度的更新。
3、自适应学习率及其改进（二阶动量）
3.1.基本概念
SGD、SGD-M 和 NAG 均是以相同的学习率去更新θ的各个分量。而深度学习模型中往往涉及大量的参数，不同参数的更新频率往往有所区别。训练后期接近极值的时候，我们希望学习率能慢慢变小。于是就引入了二阶动量，表达式如下（了解形式即可）：
其中
为t时刻参数目标函数J(θ)关于参数θi的梯度：
对角阵diag表示为
，对角线上的元素是i，i是从开始0时刻到t时刻为止，每一个θi的梯度的平方和：
学习率等效于
，即对于此前频繁更新过的参数，其二阶动量的对应分量较大，分母较大，学习率就较小。这一方法在稀疏数据的场景下表现很好。
3.2.自适应
3.2.1. Adagrad（Adaptive gradient algorithm 自适学习率应梯度下降）
我们希望能够根据参数的重要性而对不同的参数进行不同程度的更新，学习率是自适应的。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。Adagrad算法能够在训练中自动的对学习率进行调整，对于出现频率较低参数采用较大的α更新（出现次数多表明参数波动较大，）；相反，对于出现频率较高的参数采用较小的学习率更新，具体来说，每个参数的学习率反比于其历史梯度平方值总和的平方根。因此，Adagrad非常适合处理稀疏数据。
Adagrad其实是对学习率进行了一个约束即先前的算法对每一次参数更新都是采用同一个学习率，而Adagrad算法每一步采用不同的学习率进行更新,衰减系数是 历史所有梯度的平方和，其中
是上面提到的对角阵，是在t步目标函数关于θ的梯度：
对比下面传统的梯度更新公式观察一下区别：
结合开头二阶动量的定义，可简化如下表示(一般设定 β=0.9, 初始学习率η=0.001)：
特点：
- 前期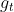较小的时候， 分母较大，能够放大梯度
- 后期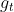较大的时候， 分母较小，能够约束梯度
- 无需手动调整梯度
- 适合处理稀疏梯度为了避免分母为0，加了一项随机扰动
缺点：
- 由公式可以看出，仍依赖于人工设置一个全局学习率，一般采用默认值0.01
- 起始梯度 η 设置过大的话，会使分母过于敏感，对梯度的调节太大
- 中后期，分母上梯度平方的累加将会越来越大，分母会不断积累使 Δθt -> 0，学习率就会收缩并最终会变得非常小使得训练提前结束
3.3.自适应的改进
RMSprop、AdaDelta这两者都是基于Adagrad的基础进行改进，相对于Adagrad会累积过去所有的梯度平方导致学习率无限变小的问题，RMSprop、AdaDelta改变了二阶动量计算方法，即用窗口滑动加权平均值计算二阶动量，将累积的动态梯度平方限制在值为w的固定大小临近窗口内。不会像Adagrad那样低效率的存储先前的所有平方梯度，而是每次取临近的窗口w内包含的动态梯度平方的均值。在t时刻的动态均值![E[g^2]_t](http://img.e-com-net.com/image/info8/a5469f7f75c64a269d37311a6b9fe8f8.gif){kind=small}
只取决于临近窗口W内的动态均值和当前的梯度
通过约束历史梯度累加，来替代累加所有历史梯度平方。这里通过在历史梯度上添加衰减因子，最终距离较远的梯度对当前的影响较小，而距离当前时刻较近的梯度对当前梯度的计算影响较大。
3.3.1. RMSprop（root mean square prop）
RMSprop解决的问题：解决Adagrad分母会不断积累，这样学习率就会收缩并最终会变得非常小的问题。RMSprop在Adagrad算法的基础上对η进行了一阶指数平滑处理，学习率系数的分母部分不再是单纯的累加，变成了滑动加权平均值，不会导致学习率消失的问题。
RMSprop算法的公式如下：
![E[g^{2}]_{t}=\beta \ast E[g^{2}]_{t-1}+(1-\beta )*g_{t}^{2}](http://img.e-com-net.com/image/info8/84907bf27b534def8215c789cd63121b.gif){kind=small}
现在，我们用历史梯度的均值替换对角矩阵
:
![\Delta \theta _{t}=-\frac{\eta }{\sqrt{E[g^{2}]_{t}+\epsilon }}\ast g_{t}](http://img.e-com-net.com/image/info8/9b9c2796a3e8404aa20ecc5ec63ba147.gif){kind=small}
我们可以使用均方根（RMS）公式简化上述过程：
![RMS[g]_{t}=\sqrt{E[g^{2}]_{t}+\epsilon }](http://img.e-com-net.com/image/info8/196ab4afdc8b44cea3f9d825009d7b8d.gif){kind=small}
![\Delta \theta _{t}=-\frac{\eta }{RMS[g]_{t}}\ast g_{t}](http://img.e-com-net.com/image/info8/9b17a320677c4f15bd33a038ce08de30.gif){kind=small}
特点：
- RMSprop依然依赖于初始学习率η
- RMSprop算是Adagrad的发展和Adadelta的变体，效果趋于二者之间
- 适合处理非平稳目标 - 对于RNN效果很好
3.3.2. AdaDelta
RMSprop优化器虽然可以对不同的权重参数自适应的改变学习率，但仍要指定超参数η，AdaDelta优化器对RMSprop算法进一步优化。首先梯度更新公式如下：
![E[g^{2}]_{t}=\beta _{1} \ast E[g^{2}]_{t-1}+(1-\beta _{1} )*g_{t}^{2}](http://img.e-com-net.com/image/info8/860b6797be894dfdb525aaa89976bf75.gif){kind=small}
梯度更新过程如下：
前面讲过，在Adagrad中求导得到的参数更新形式为：
现在，我们用历史梯度的均值替换对角矩阵：
我们可以使用均方根（RMS）公式简化上述过程：
优化学习率：
显然上述部分和RMSprop是相同的，此时Δθ的变化还是和η有关，而与RMSprop和Adagrad的区别是，AdaDelta引入了一个变量
，来记录每次 “θ参数更新的差值
” 的平方的指数加权移动平均值。通过牛顿法和Hession矩阵结合，使用自变量θ更新量的平方的指数加权移动平均值来替代RMSprop中的学习率η.
作者在文章[Zeiler M D, 2012. Adadelta: An adaptive learning rate method]中定义，使用
来记录J(θ)自变量θ的变化量，即自变量参数θ每次更新的差值的平方的指数加权移动平均：
从下式可以看出，我们不再用随机设的一个初始值η，而是用自变量θ每次更新的差值的平方的指数加权移动平均，来作为学习率，这样比用随机的η更有意义，由于t时刻自变量θ尚未更新，所以只能用
来近似代替，初始状态下
：
![\Delta g_t=\frac{\sqrt{\Delta x_{t-1}+\epsilon }}{\sqrt{E[g^2]_t - \epsilon }}*{g_t}](http://img.e-com-net.com/image/info8/d6f496842bd84807a973d8e7e71add2b.gif){kind=small}
然后再更新自变量θ，从而达到更新J(θ)的效果：
注：
留意上面和含义的区别，是指J(θ)的梯度，而是参数θ每次更新的差值，即
，然而当前计算出的更新差值，又会影响下一次学习率的大小。
即RMSprop更新梯度使用的学习率系数是：
![\frac{\eta}{\sqrt{E[g^2]_t - \epsilon }}](http://img.e-com-net.com/image/info8/d5db1ceeb96c42f9a963f65a14c9e997.gif){kind=small}
而AdaDelta使用的学习率系数是：
![\frac{\sqrt{\Delta x_{t-1}+\epsilon }}{\sqrt{E[g^2]_t - \epsilon }}](http://img.e-com-net.com/image/info8/af45e2a759fe4a70be1356edea77998c.gif){kind=small}
随着训练轮次增多，θ的梯度越来越平缓，则值越来越小，则也会随之变小，影响学习率系数的也会越来越小，即可使得学习率越来越小，函数收敛。此时我们也就不在需要手动设置学习率，而是用
替代了η。
4、自适应动量更新
4.1.Adam
集成动量+自适应学习率的优化算法应该是目前最好的。结合了 自适应学习策略Adagrad 和 Momentum的更新思想。
梯度更新算法介绍:
Adam = Adaptive + Momentum，顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量，分别计算其指数加权移动平均。公式如下，m表达式定义为一阶动量，v表达式定义为二阶动量。初始状态时m1=0，v1=0，默认β1=0.9，β2=0.999：
从上式可以看出，一阶动量和二阶动量的区别就是对梯度进行了平方计算，一阶动量m控制梯度下降的方向，二阶动量v控制梯度下降的步长。我们简单的对m进行三次迭代，然后分析结果：
从上式可以看出，当m进行很多次迭代之后，早期的梯度g会随着系数β的累乘而逐渐趋向于0，即所占的权重越来越小，近期的梯度会更大。但在初始计算动量时会出现梯度动量较小的问题，当β1=0.9时，
，导致梯度过小，更新过慢，为了消除这个影响，对m和v的梯度进行偏差修正如下：
修正过程如下：
最终利用一阶动量m和二阶动量v定义梯度更新规则如下：
Adam 算法和传统的随机梯度下降不同。传统的随机梯度下降保持单一的学习率更新所有的权重，学习率在训练过程中并不会改变，或学习率会单调递减直到趋于0。而 Adam 通过随机梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。
对于
的形式，
相当于是对不同参数分量梯度的一个惩罚参数。如果一个参数经常更新则积累的值就较大，因此频繁更新的参数单个异常样本就不会对学习率产生较大影响，可以较好的保留历史学习梯度。反之较少更新的参数分量会对学习率带来较大影响，有利于修改梯度加快对参数的学习。频繁更新的梯度将会被赋予一个较小的学习率，而稀疏的梯度（更新频率少的梯度）则会被赋予一个较大的学习率。
Adam 算法的提出者描述其为两种随机梯度下降扩展式的优点集合，即：
-
适应性梯度算法为每一个参数保留一个学习率以提升在稀疏梯度上的性能，提供解决稀疏梯度和噪声问题的优化方法。即稀疏梯度是指梯度较多为0的情况，由于adam引入了动量法，在梯度是0的时候，还有之前更新时的梯度存在，还能继续更新；噪声问题是对于梯度来说有一个小波折（类似于下山时路不平有个小坑）即多个小极值点，可以跨过去，不至于陷在里面。
-
均方根传播（RMSProp）基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。
-
因为一阶动量，为不同的参数计算不同的自适应学习率，首先默认（1-β1）等于100倍的（1-β2），
Adam 算法同时获得了 AdaGrad 和 RMSProp 算法的优点。Adam 不仅如 RMSProp 算法那样基于一阶矩均值计算适应性参数学习率，它同时还充分利用了梯度的二阶矩均值（即有偏方差）。具体来说，算法计算了梯度的指数移动均值，超参数 β1，β2控制了这些移动均值的衰减率，前者控制一阶动量，后者控制二阶动量。移动均值的初始值和 β1，β2值接近于 1（推荐值），因此矩估计的偏差接近于 0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。
4.2.NAdam(融合NAG的Adam)
Nadam和Adamax本质是对adam的一些小改进，Nadam是Adam+NAG的融合，使用动量的时候不是使用当前的动量，而是像NAG一样，向未来多走一步，取下一时刻的动量，同样是为了达到减少收敛过程中的震荡，少走冤枉路的效果。
推导过程如下图：
4.3.Adamax
Nadam和Adamax本质是对adam的一些小改进，adamax对adam的分母部分v，不再每次使用最新迭代的值v，而是直接取历史迭代中v的最大值max(v)作为分母。
推导过程如下图：
五、如何选择
如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam,Nadam,Adamax。
RMSprop, Adadelta, Adam,Adamax,Nadam 在很多情况下的效果差别不大。
Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，随着梯度变的稀疏，Adam 比 RMSprop 效果会好。
从效率和学习成本的角度整体来讲，Adam 是最好的选择。Adam是傻瓜式数码相机，SGD是复杂的单反，对一般人来说发朋友圈数码相机就够了，但参加摄影比赛还是得用单反。
很多论文里都会用 SGD，没有 momentum 等。SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点。因此现在很多人都在用“前期Adam”+“后期SGD”相结合的方法，达到前期提速、逃离鞍点，后期提升精度的效果。
参考文献：
《神经网络与深度学习》中的AdaDelta算法如何理解？ - 知乎 (zhihu.com)
#深入探究# Adam和SGDM优化器的对比 - 知乎 (zhihu.com)
通俗理解 Adam 优化器_energy_百分百的博客-CSDN博客_adam优化器
ADAM与二阶优化算法的联系 - 知乎 (zhihu.com)
（转）优化时该用SGD，还是用Adam？——绝对干货满满！ - 程序员大本营 (pianshen.com)
【转】听说你了解深度学习最常用的学习算法：Adam优化算法？-阿里云开发者社区 (aliyun.com)
#深度解析# 深度学习中的SGD、BGD、MBGD、Momentum、NAG、Adagrad、Adadelta，RMSprop、Adam优化器_energy_百分百的博客-CSDN博客_adagrad
自适应矩估计Adam优化算法 - 简书 (jianshu.com)
SGD、Adam等深度学习优化算法综述 - 知乎 (zhihu.com)
【数理统计】参数估计及相关（点估计、矩估计法、最大似然估计、原点矩&中心距）_火柴先生的博客-CSDN博客_中心矩估计
深度学习总结（一）各种优化算法_monkey512的博客-CSDN博客_优化算法
从 SGD 到 Adam —— 深度学习优化算法概览(一) - 知乎 (zhihu.com)
SGD、Adam等深度学习优化算法综述 - 知乎 (zhihu.com)