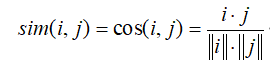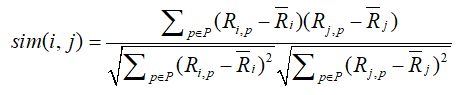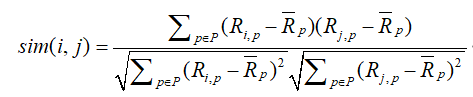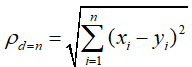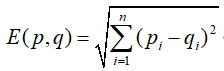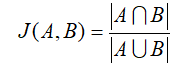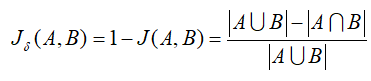推荐算法中常用的几种相似度计算方法
无论在信息检索(Information retrieval,IR)或是在推荐系统(Recommendation system,RS)中,其一般思路就是先进行合理的数据处理,再计算相似度,从而得出结果.如在推荐系统中,首先需要获取用户或物品的数据,并同构合理的表示函数来构造用户或物品的Embedding,然后就是计算用户之间的相似度或者物品之间的相似性.而主要的相似性计算方法主要有以下几种:
1.余弦相似度(Cosine similarity)
余弦相似度用来衡量用户向量![]() 和
和![]() 之间的向量夹角大小,夹角越小,证明余弦相似度越大,说明两个用户越相似,若把用户向量换成物品向量,则同理可得物品向量之间的相似度.
之间的向量夹角大小,夹角越小,证明余弦相似度越大,说明两个用户越相似,若把用户向量换成物品向量,则同理可得物品向量之间的相似度.
2.皮尔逊相关系数(Pearson Correlation Coefficient)
皮尔逊相关系数在对用户进行相似性计算时,与余弦相似度相比,加入了用户平均分对各独立评分进行修正,减小了用户评分偏置的影响.
其中,![]() 表示用户
表示用户![]() 对物品
对物品![]() 的评分,
的评分,![]() 表示用户
表示用户![]() 对所有物品的平均评分,
对所有物品的平均评分, ![]() 代表所有物品的集合.这里引入了用户对所有物品的平均评分,这里也可以引入物品
代表所有物品的集合.这里引入了用户对所有物品的平均评分,这里也可以引入物品![]() 的平均评分,即:
的平均评分,即:
3.欧几里得距离(Euclidean Distance)
这里的欧几里得距离指的是![]() 维空间中两点之间的距离,比如在二维空间上,两点的距离 定义为:
维空间中两点之间的距离,比如在二维空间上,两点的距离 定义为:
同理,三维的为:
故![]() 维空间的表达式为:
维空间的表达式为:
而我们在推荐时的相似度计算主要用于向量之间的相似度计算,也就是求![]() 维向量之间的距离,比如同一空间内的两个向量
维向量之间的距离,比如同一空间内的两个向量![]() 和
和![]() ,它们是同一空间内的两个点,那么欧氏距离就是衡量这两个点之间的距离:
,它们是同一空间内的两个点,那么欧氏距离就是衡量这两个点之间的距离:
欧氏距离是一个非负数,最大值为正无穷,通常计算相似度的结果希望是[-1,1]或[0,1]之间,故一般可以使用:
[注]:欧氏距离不适用于布尔向量之间的计算.
4.杰卡德距离(Jaccard Distance)
(1)杰卡德相关系数
杰卡德相关系数指的是两个集合A和B的交集在其二者的并集中所占的比例
(2)杰卡德距离
与杰卡德相关系数相反,杰卡德距离使用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度: