密文检索论文阅读

保序加密OPE 算法 BCLO09及python仿真

“best-possible” security, i.e.,IND-OCPA security. It means that the ciphertext should reveal nothing about the underlying plaintexts other than the ordering.

Enabling Efficient and Geometric Range Query With Access Control Over Encrypted Spatial Data

通过对加密空间数据的访问控制，实现高效的几何范围查询

摘要

作为一种基本的查询功能，范围查询已经被用于许多场景，如SQL检索、基于位置的服务和计算几何。同时，随着数据量的爆炸式增长，用户越来越倾向于将数据存储在云上，以节省本地存储和计算成本。但长期存在的一个问题是，用户的数据可能会完全泄露给云服务器，因为云服务器拥有完全的数据访问权。为了解决这一问题，常用的方法是将原始数据加密后再外包，但这会大大降低数据的可用性和可操作性。本文提出了一种有效的几何范围查询方案(EGRQ)，该方案支持加密空间数据的搜索和访问控制。我们采用安全的KNN计算、多项式拟合技术和保序加密来实现云数据上安全、高效、准确的几何范围查询。在此基础上，提出了一种新的空间数据访问控制策略来细化用户权限EGRQ。为了提高搜索效率，在整个搜索过程中采用r -树来减少搜索空间和匹配时间。最后，从理论上证明了系统的安全性我们的从空间数据的保密性、索引和活板门的隐私保护以及活板门的不链接性等方面提出了方案。此外，大量的实验表明，与现有的方案相比，我们提出的模型具有较高的效率。

系统模型、威胁模型和安全要求

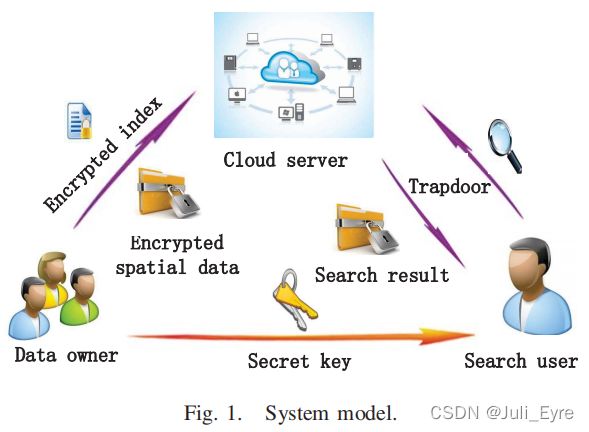
System Model

• 数据所有者：数据所有者的主要任务是将其空间数据以密文的形式提交到云服务器。为了提高检索效率，对于每个原始数据，数据所有者将创建一个与之关联的加密索引。然后将密文和索引都发送到云服务器。
• 云服务器：由于其强大的计算和存储能力，用户的数据被存储在云服务器上。此外，一旦云服务器收到搜索用户的查询请求（即trapdoor），就会对加密的云数据进行一系列计算，相应的搜索结果返回给合法实体。
• 搜索用户：当密钥传递给搜索用户时，将生成相应的加密查询请求（即trapdoor）并发送到云服务器。此外，在从云服务器接收到搜索结果后，搜索用户使用该密钥脱机解密这些结果。

Threat Model and Security Requirements

云服务器一直被认为是“诚实但令人好奇”的[23]，[36]，[37]。具体来说，一方面，云服务器严格、诚实地执行搜索用户提交的搜索请求，并将实际结果返回给授权用户。另一方面，云服务器可能会对用户的敏感数据感到“好奇”，并试图出于非法利益或经济激励而窃取它们。基于这种情况，我们考虑了两种威胁模型depending on云服务器可用的信息:

• Known Ciphertext Model: In this model, only encrypted original data, index and trapddor are known to the cloud server, except that, it knows nothing.
• Known Background Model: In this stronger model, we generally assume the cloud server holding more information such as the distribution both of data and user’s search requests comparing with known ciphertext model. In other words, extensive data analysis of a known database being similar to the target database have been investigated prior by the cloud server

Based on the above threat models, we define the security requirements as follows:

• 空间数据的保密性：考虑到空间数据的隐私性，原始数据在外包给云服务器之前，应采用AES等对称加密技术进行加密。因此，对于每个数据，它只能由数据所有者和授权的搜索用户访问。
• 索引和活板门的隐私保护Privacy protection of index and trapdoor：生成索引和活板门是为了提高EGRQ的匹配效率。由于索引和活板门与相应的用户数据相关，一旦加密的用户数据泄露，云服务器可以恢复部分信息。因此，应做好索引和活板门的隐私保护
• 活板门的不可链接性Unlinkability of trapdoor: 活板门的不可链接性意味着云服务器无法区分任意两个任意的活板门是否来自同一搜索请求。因为在现实的场景中，相同的搜索请求可能会在一段时间内频繁地提交到云服务器。如果云服务器能够轻松识别它们，它就可以推断出活板门之间的连接，并威胁到实际搜索请求的隐私。因此，对于相同的搜索请求，活板门应该随机生成，而不是确定性生成

PRELIMINARIES

为了方便起见，本节回顾了一些基本的理论知识，如安全kNN计算、保顺序加密(OPE)和多项式拟合技术，这些知识也在我们提出的方案中发挥了基石作用

Secure kNN Computation

k-nearest neighbor (kNN) can calculate the inner product of two vectors under encrypted data privately.
Generally speaking, secure kNN computation is usually made up of four parts: SkC_Initialization, SkC_GenIndex, SkC_GenTrapdoor and SkC_Query:

• SkC_Initialization：数据所有者随机初始化密钥ψ=(sk1，S，M1，M2)，其中sk1表示用于加密原始空间数据的对称加密(如AES)的密钥，S表示(N+3±++T)维二进制向量来分割明文向量S indicates a (N + 3 + κ + T )-dimensional binary vector exploited to split plaintext vectors，${\mathbf{M}}_1,{\mathbf{M}}_2$表示两个(N+3+κ+T)×(N+3+κ+T)维可逆矩阵，用于分割后对向量进行加密。然后，密钥ψ将通过一个安全通道发送给搜索用户。
• SkC_GenIndex：首先，原始的空间数据将使用密钥sk1进行加密。然后，为每个空间数据i生成一个(N+3+κ+T)维向量Mi，其中1≤i≤k，然后利用二进制向量S将$M_i$随机分裂为$M_{ia}$和$M_{ib}$。具体地说，如果S[j]=0，(j=0,1···，N+2+κ+T)，$M_{ia}[j]$和$M_{ib}[j]$将被设置为$M_{ia}[j]=M_{ib}[j]=M_i[j]$。否则，它将被随机划分为$M_i[j]=M_{ia}[j]+M_{ib}[j]$。因此，加密后的索引可以表示为$R_i=M_{ia}{\mathbf{M}}_1,M_{ib}{\mathbf{M}}_2$，并提交到云服务器
• 

Order-Preserving Encryption

订单保存加密(OPE)[39]，是指在加密后可以保持data orders不变(即，如果m1>m2，[m1]>[m2])，其中，我们使用[·]来表示保持顺序加密的密文。由于这一特殊特性，OPE已被应用于许多安全范围查询场景，如位置查找、数据挖掘和其他基于位置的服务.
一般来说，对称OPE方案包括KeyGen、Enc和Dec三种基本算法。具体来说，

本文将利用OPE的特性来实现加密空间数据之间的比较操作，从而缩小查询范围，显著提高搜索效率.

Access Control Strategy

在我们提出的方案中，我们设计了一种新的空间数据访问控制策略，这样，每个搜索用户只能访问由自己自己授权的用户数据。例如，如果将角色$a_i$分配给搜索用户j，则只能向与$a_i$关联的原始搜索用户j查询空间数据。
具体来说，假设有κ角色集为κ=(n1，n2，···nκ)，对于每个空间数据，构造如下多项式：

可以将用户对特定空间数据是否具有访问权限的问题简化为检查其访问角色是否为目标多项式的根的问题

多项式拟合

r树

主要功能是根据空间中点之间的距离对空间数据进行分类

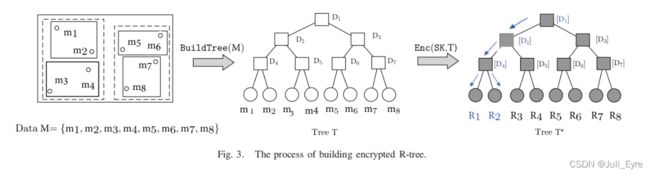
如图3所示，每个叶节点表示一个空间数据，每个非叶节点表示由矩形组成的范围，其中mi和Dj分别表示矩形的数据记录和范围，[Dj]和Ri表示加密的Dj和索引，(i=1、2、···、8、j=1、2、···、7)。一般来说，给定一个搜索请求（即一个搜索矩形），R-tree的遍历过程描述如下：

• 从根节点开始，遍历整个树，找到所有与给定的搜索矩形相交的最深的非叶节点，如果存在，则继续进行下一步操作。否则，将返回null。
• 对于上面非叶节点中包含的每个点，检查它是否满足III-C节中所示的标准。如果满足，则返回这些点给搜索用户。否则，返回null。

PROPOSED SCHEME

我们提出了一种有效的几何范围查询方案(EGRQ)，支持对加密空间数据的搜索和数据访问控制。我们将从以下小节中详细说明EGRQ

Initialization

GenIndex

为了保护原始空间数据的机密性，所有用户的原始数据在输出到云服务器之前都将被加密(使用AES)。

数据库查询处理的拓扑转换方法

本文提出了一种将特征空间转换为新的特征空间的新方法，即将原始空间中的范围查询映射到转换空间中的等价方框查询中。由于方框查询是轴对齐的，因此有几个实现优势，可以利用使用R-Tree[9]等索引方案来加快查询结果的检索速度。对于二维数据，转换是精确的。对于大于二维的空间，我们提出了一种基于不相交平面旋转的空间变换方案和一种新的查询类型，即剪枝框查询，以得到精确的结果。在大型合成数据库和一些真实数据库上的实验结果表明，所提出的变换方案的有效性。这些实验结果已被合适的数学模型所证实。在不相交的平面器旋转中，需要额外的计算时间来消除由于边界框不精确而产生的假阳性。提出了第二种基于优化边界盒的拓扑变换方案，减少了误报的数量。这种减少的量随着维度的增加而增加。基于一种新的同步局部最优投影方法，计算了高维空间的优化边界盒。

introduce

在数据库系统中使用的一些最常见的查询类型是范围查询和方框查询。使用L1空间的范围查询有许多应用领域，包括地理信息系统、图像数据库和生物信息学。在本文中，我们主要关注L1空间中范围查询的实现，并使用等效的框查询来优化该实现

Geo-DRS: Geometric Dynamic Range Search on Spatial Data with Backward and Content Privacy

最常见的Searchable Symmetric Encryption (SSE)泄漏功能是访问模式和搜索模式。访问模式会泄漏匹配搜索查询的所有文件标识符。相比之下，搜索模式会泄漏对搜索查询的重复（即，可以确定两个搜索标记是否对应于同一个查询）。利用SSE泄漏可能使对手（通常是诚实但好奇的云服务器）推断出关于数据库的超出SSE方案中考虑的信息（例如泄漏滥用攻击[8,23]）。

大多数支持几何范围搜索的现有SSE方案都是在静态设置中设计的（即，在设置后更新数据库记录是不可能的，或者以重新加密和重新上传数据库为代价）。虽然动态设置为方案提供了更多的灵活性，并支持更多的真实应用程序，但它引入了更多的泄漏。为了在动态设置中捕获新的泄漏，Bost等人[5]引入了动态SSE的安全概念，即所谓的向前和向后隐私。最近，Kasra-克尔曼等[15]表明，可能有额外的泄漏在处理几何数据不被博的向前和向后隐私模型，并引入了一个新的安全概念of dynamic SSE over spatial data（称为内容隐私），隐藏的访问模式在搜索和更新操作。

不同的加密原语已被用于支持对几何数据的安全范围搜索，如保持顺序加密(OPE)、 somewhat/fully homomorphic encryption, Geohash等。然而，由于与几何范围搜索相关的固有泄漏，大多数无法抵抗针对GRS的SSE方案新开发的泄漏滥用攻击。

贡献

在本文中，我们提出了两种动态可搜索的对称加密方案，即Geo-DRS和Geo-DRS+。第一种方案说明了一种使用R+树支持几何范围搜索的新方法，其中需要客户端和服务器之间更多的往返来实现内容隐私（或者同态加密可以以更高的计算成本使用）。我们的Geo-DRS+方案通过利用$Z_2$中的R+树和秘密共享，提供了一个有效的动态范围搜索。此外，它使用两个不结盟的服务器去避免客户端到服务器的多轮交互。因此，在搜索和更新期间，它在客户端和服务器之间只有一次往返，两个服务器之间的通信轮数为对数。Geo-DRS+是高效和可扩展的，同时对Full Database Reconstruction (FDR) and Approximate Database Reconstruction (ADR)攻击具有弹性。我们的安全分析表明，Geo-DRS+是backward and content private.

R-Tree and R+tree

R-tree是由安东宁·古特曼在1984年[12]首次提出的，以有效地处理空间数据。这个数据结构是一个高度平衡的树状结构，其叶节点中的索引记录包含指向数据对象的指针。在本文中，我们使用R+树[25]，这是R树的一种变体，避免了中间节点上的重叠矩形。此外，R+树相比R-树具有更好的搜索性能。如图所示。通过1、2和3来查看树是如何形成R+树的(为了简单起见，本例中没有提到边界框(Rect)的值)。

在R+树中，叶节点由(ID，Rect)组成，其中ID是对象的标识符，Rect表示对象所在的边界框。也就是说，Rect=(xmin，xmax，ymin，ymax)，它是左下角的坐标和右上角的坐标。非叶节点包含表单项(p，Rect)，其中p是指向下节点（子节点）地址的指针，Rect覆盖了下节点条目中的矩形。R+树具有以下属性：

• 对于中间节点中的每个条目(p，Rect)，当且仅当R被Rect覆盖时，相应的子树包含一个矩形R，除非R是一个叶节点上的一个矩形；在这种情况下，R只能与Rect重叠。
• 在一个中间节点中的任何两个条目中都没有重叠。
• 这个根至少有两个子代，除非它是一片叶子。
• 所有的叶子都在相同的水平/高度

安全的逐位比较

这项工作使用了基于位秘密共享的安全两方计算。x∈z2的附加秘密共享由两个共享x1和x2组成，受x=x1+x2mod2的约束。这两个共享分别被分配到两个服务器上。我们将用[[x]]来表示这个秘密共享所有的秘密共享操作都是模2，为了简洁起见，省略了模符号。注给定秘密共享[[x]]和[[y]]，，这两个服务器可以在本地共享以一种简单的方式计算对应于z=x+y的秘密共享

Syntax of Our Geometric Dynamic Range Search (Geo-DRS+)

我们的几何动态范围搜索(Geo-DRS+)方案包括以下算法：

1. Setup(DB)：第一步是生成要外包给服务器的数据库记录的共享the shares。此阶段由数据所有者运行，如下所示：

• Build。R+tree(DB，m)→(RT)：给定一个数据库DB和树参数m（决定每个节点中点的最大数量），该算法输出一个高度平衡的R+树。
• 秘密共享(RT)→(S1，S2)：该算法获得R+树作为输入，并输出其按位排列的秘密共享。
  The Setup阶段还生成乘法三组(执行协议GEQ所需要的)和数据库状态δ。S1给第一个服务器，S2给第二个服务器
  

2. $Search（Rec{t}_q/S1/S2）$是客户端和服务器之间的协议。为了找到理想的范围查询$Rec{t}_q$， the client secret shares the query coordinates with the servers whom run the GEQ protocol over their stored shares S1/S2 traversing the R+tree jointly to find the minimum bounding boxes (leaf nodes) that cover the query. The servers output the shares of the result set, R1和R2.
3. Update(ni, δ、S1/S2)是数据所有者和服务器之间的协议。要插入或删除对象，数据所有者应该生成相应叶节点的新共享。在接收到共享后，服务器通过将其替换为新的共享来更新其存储的共享S1/S2。最后，服务器将数据集状态更新为δ+1。

Generic Dynamic SSE Leakage Functions

泄漏函数L保持查询列表Q的状态，即迄今为止发出的所有查询的列表。

在加密的空间数据上的几何范围搜索Geometric Range Search on Encrypted Spatial Data

摘要

几何范围搜索是SQL和NoSQL数据库中空间数据分析的基本原语。它在基于位置的服务、计算机辅助设计和计算几何方面有广泛的应用。由于数据规模的急剧增加，公司和组织有必要将其空间数据集外包给第三方云服务(如Amazon)，以减少存储和查询处理成本，但同时，承诺不会将隐私泄露给第三方。可搜索加密是一种对加密数据执行有意义的查询而不透露隐私的技术。然而，对空间数据的几何范围搜索尚未得到充分的研究，也没有得到现有的可搜索加密方案的支持。在本文中，我们设计了一种对称密钥搜索加密方案，可以支持加密空间数据的几何范围查询。我们的主要贡献之一是，我们的设计是一种通用的方法，它可以支持不同类型的几何范围查询。换句话说，我们对加密数据的设计独立于几何范围查询的形状。此外，我们进一步扩展了我们的方案，进一步使用了树状结构，以实现比线性更快的搜索复杂性。我们正式地定义并证明了我们的方案在选择性选择的明文攻击下具有不可分辨性的安全性，并在一个真实的云平台(AmazonEC2)上通过实验证明了我们的方案的性能。

引入

几何范围搜索[1]，[2]是对空间数据执行的最基本的查询之一，其中数据被表示为点，而查询可以被描述为几何对象，如三角形、圆、矩形。它是一个不可或缺的功能，包含在大多数SQL和NoSQL数据库中。例如，主要的数据库应用程序，如MySQL、Oracle、PostgreSQL(附加使用PostGIS)和MongoDB，都提供了某些类型的几何范围搜索。在空间数据集上进行几何范围搜索的目的是检索在特定几何范围内的点（参见图1中的一些主要类型的几何范围查询）。

例如，移动用户可以通过在空间数据集[3]上运行循环范围搜索，在基于位置的服务中找到兴趣点、朋友、咖啡馆或邻近的事件，如Yelp和四方；数据分析器可以通过评估多轮循环范围查询[4]，基于数百万用户的位置登录来研究社会可达性；如果在空间数据集上进行几何范围搜索，设计者可以计算出有多少房屋、建筑和道路会受到影响，其中机场的形状可以表示为矩形或三角形[5]；医学研究者可能需要查询空间数据集，以收集某一几何区域（如城市）的特定疾病（如埃博拉病毒）患者的信息，以预测是否会发生危险的爆发。

对于公司/组织来说，在本地维护大量的数据不再容易，甚至不再有利可图。因此，我们经常看到公司和组织，甚至是主要的组织将他们的数据集（包括空间数据集）外包给公共云提供商。然而，由于安全和隐私事件不断地在云计算中发生，将数据集外包给公共云服务也增加了这些公司及其用户[17]，[18]对隐私的担忧。特别是，通过损害云服务，内部攻击者（例如，好奇的云管理员）很容易泄露这些公司的数据隐私并查询用户的隐私，由于法律和商业问题或数据本身的敏感性，这些应该被保密。

在将数据集外包到公共云之前，直接使用传统的加密技术(例如，AES-CBC[19])，这可能是防止上述隐私泄露的最简单的方法。利用这种方法的应用程序包括Wuala。然而，它不可避免地在加密数据的搜索功能方面引入了障碍。因此，提出了可搜索加密[17]，允许客户端管理密文域中的常规搜索操作，而不向客户端不完全信任的公共云揭示数据隐私或查询隐私。

虽然大多数可搜索的加密方案[17]，[20]-[29]专注于常见的SQL查询，如关键字查询和布尔查询，但很少有研究专门研究加密空间数据的几何范围搜索。更具体地说，以前的可搜索加密，特别是处理顺序比较[6]-[9]，[13]，[14]或顺序保持加密(OPE)[10]-[12]可以简单地扩展和利用，以实现空间数据的轴平行矩形范围搜索。最近，Wang等人提出了一种新的方案[15]，专门利用一组同心圆专门对加密数据执行循环范围查询。不幸的是，这些以前的工作都没有特别研究过用非轴-平行的矩形或三角形表示的几何范围查询。更重要的是，目前还缺乏一种通用的方法，它可以灵活、安全地支持对加密空间数据的不同类型的几何范围查询，而不管它们的特定几何形状如何

本文提出了一种对称密钥概率几何范围可搜索加密方法。通过我们的方案，一个半诚实（即诚实但好奇的)云服务器可以验证一个点是否在加密的空间数据集的几何范围内。非正式地说，除了学习几何范围搜索的必要布尔搜索结果（即内部或外部）外，半诚实的云服务器不能显示任何关于数据或查询的私有信息。我们的主要贡献总结如下：

• 提出了一个对称密钥概率几何范围可搜索加密，并正式定义并证明了其在选择性选择纯文攻击(IND-SCPA)[30]下具有不可分辨性的安全性。此外，我们的搜索过程对加密的数据是非交互式的。在搜索复杂度方面，我们的基线方案具有线性复杂度（关于数据记录的数量），其高级版本通过集成树状结构(即R-trees[31]，[32])来实现快速线性搜索。
• 我们的设计是一种通用的方法，它可以安全地支持对加密的空间数据的不同类型的几何范围查询，而不管它们的几何形状如何。此外，我们的设计不仅适用于几何范围查询，而且还兼容其他常规类型的几何查询，如交叉查询和点框查询[5]。
• 我们利用AmazonEC2来评估我们的方案在加密的空间数据上的性能。此外，我们还演示了通过使用几种不同的方法来提高我们设计的性能，包括r树、基于格的加密原语和部分加密

RELATED WORK AND CHALLENGE

正如我们所提到的，大多数可搜索的加密方案[17]，[20]-[29]都集中于关键字搜索（通常使用反向索引或字典），而这并不适用于空间数据。在本节中，我们将介绍一些与加密数据的几何范围搜索密切相关的工作。此外，我们还解释了设计一个安全的几何范围搜索的一般解的挑战。

Axis-Parallel Rectangular Range Search

一些以前的可搜索加密处理顺序比较 基本上可以管理加密空间数据的轴平行矩形范围搜索。类似地，保持顺序的加密[10]-[12]的隐私保证比可搜索的加密更弱，它也能够通过简单的扩展执行轴并行矩形范围搜索。Ghinita和Rughinis[33]特别利用某些具有分层编码的功能加密[6]，在移动用户监控的应用中，有效地对加密的空间数据进行轴-平行矩形范围搜索。

不幸的是，它们都不能直接支持其他类型的几何范围查询，如非轴平行的矩形、圆和三角形。请注意，为任何几何对象生成最小边界轴平行矩形，例如三角形、圆或非轴平行矩形，将是上述方案构建支持不同类型几何范围查询的通用解决方案的替代选项。然而，这种替代方法将引入较高的假阳性率，这些假阳性表明点在最小边界轴平行矩形内，而不在原始几何对象内（见图）。此外，这些假阳性在更高的维度上会变得更糟。

图：对于不同类型的几何对象的最小边界轴-平行矩形，其中黑暗区域代表所有的假阳性。

Circular Range Search

最近的一项工作能够特别管理加密空间数据的圆形范围搜索。它的主要想法是利用一组同心圆来表示一个圆形范围查询。更具体地说，如果一个数据点位于圆形范围查询生成的一个同心圆的边界上，那么它就是循环范围查询内的一个点。然而，这种带有同心圆的想法只适用于圆形范围查询，而不适用于其他几何范围查询

Secure Multi-Party Computation on Computational Geometry

在计算几何上的安全多方计算中，[34]，[35]之前的工作也与本文所研究的主题密切相关。通过这些工作，双方(例如，Alice和Bob)能够私下计算和测试一个点是否在一个几何范围内。类似地，最近的一些工作[3]，[36]在私人接近测试，可以帮助两个用户安全地验证一个用户是否在另一个用户的私人位置，也由安全的多方计算[37]构建。然而，这些基于安全多方计算的工作通常需要双方之间进行广泛的交互。而我们的目标是在对加密数据进行评估时没有交互的设计

Challenges for Building a General Solution

通常，我们有一些标准的方法来测试一个点是否在明文域[2]中的一个几何对象内。例如，为了检查一个点是否在一个轴平行的矩形内，我们可以分别将一个点的X轴和Y轴与这个轴平行的矩形的左下角和右上角的X轴和Y轴进行比较。对于圆形范围搜索，我们可以简单地计算一个点与查询圆的中心之间的距离，然后将此距离与查询圆的半径进行比较。对于其他表示更一般多边形形式的几何范围搜索，如非轴平行矩形和三角形，我们可以计算交叉积，并将交叉积的结果与0（即正或负）[5]进行比较。不幸的是，直接使用不同的方法对加密数据操作前面的几何范围查询将给设计通用几何范围可搜索加密带来挑战，该加密有望灵活地支持不同类型的几何范围查询。

首先，由于完全同态加密在任意函数上的效率低下，实际上对加密数据评估不同类型的操作通常依赖于不同的加密原语。例如，保留顺序的加密只适用于计算顺序比较；确定性加密（例如，伪随机函数[19]）只用于等式检查；加性同态加密只适用于加法。因此，以并行或洋葱的方式利用不同的加密原语(例如，[40]中的CryptDB)可以同时支持对加密数据的不同操作，但它不可避免地会引入额外的开销，用于初始化系统、管理多个密钥以及生成具有不同原语的多个密文。

更重要的是，一些几何范围查询不仅需要执行不同的操作，而且还需要在密文域中连续地执行这些操作。例如，假设直接遵循我们上面介绍的明文域的逻辑，安全循环或安全三角形范围搜索，基本上涉及对加密数据的计算和比较操作，其中甚至以并行或onion manner的方式利用不同的加密原语也是不够的。在这种情况下，简单地应用混乱的电路将是一个选择。因为，从理论上讲，任何计算（包括几何范围查询的计算）都可以被描述为一组电路.

然而，混乱电路的使用要求客户端一直在线，这就引入了多轮客户机到服务器的交互和显著的通信开销，特别是对于复杂的电路。更糟糕的是，混乱的电路通常只能使用一次，而搜索应用程序通常涉及大量的查询。另一方面，使用两个（或更多）非合并服务器将是一种解决方案，以避免多轮客户端-服务器交互，同时仍然在密文域[43]-[45]中连续评估不同的操作。通常，这种方法的基本思想是利用服务器到服务器的交互来最小化客户端到服务器的交互。不幸的是，与传统的单服务器模型相比，使用两个（或更多）非合并服务器的假设不太实用。

因此，建立一个通用的几何范围可搜索加密是一项艰巨的任务，它可以执行不同类型的范围查询。此外，设计一个使用单服务器模型对加密数据进行非交互式评估的通用评估甚至是具有挑战性的。

方案

System and Threat Model

图3所示的我们的方案的系统模型包括数据所有者、数据用户和云服务器。数据所有者（例如，一个公司或组织）将其数据集存储在云服务器上，以降低数据存储和查询处理的本地成本。数据用户（例如，公司的用户或组织的用户）希望在云中搜索外包的空间数据集。云服务器提供数据存储和搜索服务。请注意，数据所有者本身总是有能力搜索外包的空间数据。在这项工作中，我们重点关注空间数据的几何范围查询。它意味着空间数据集中的每个数据记录都表示为一个点，而每个几何范围查询都可以表示为一个几何对象，如矩形、三角形或圆。几何范围查询的目的是检索位于几何范围内的点。

云服务器是一个半诚实（即诚实但好奇）的实体，这表明它提供了可靠的服务，但它将尝试学习关于数据记录和几何范围查询的私人信息。为了保留私有信息泄漏，数据所有者只在云服务器上存储其空间数据集的加密形式，而客户端（数据用户或数据所有者）只提交几何范围查询的加密版本（即，一个搜索令牌）给云服务器。

Definitions of GRSE

1）符号：在下面，我们首先澄清一些将在本文的其余部分中经常使用的符号。然后，我们正式地给出了对称密钥几何范围可搜索加密(GRSE)的定义。
首先，我们假设我们在本文中处理的数据都是正整数（或其他可以平滑地转换为正整数）。我们利用$\Delta T^w$来表示数据空间，其中w是维数，T是每个维度的大小。为了便于描述，我们将主要关注w=2和每个维度的大小相同的情况(即Tk=T，对于1≤k≤w)。因此，数据记录D本质上是数据空间$\Delta T^w$中的一个w维点，其中每个维度中这个点的值在[0，T−1]范围内，我们有D∈$\Delta T^w$。数据集D是点的一组D={D1，…，Dn}，其中n是数据集中的数据记录的数量。

本质上，几何范围查询Q是一个几何对象。本文所考虑的几何对象的主要类型包括矩形、圆和三角形。由于每个几何对象代表一个封闭区域，它覆盖了数据空间$\Delta T^w$中一定数量的点，每个几何对象本质上可以表示为数据空间中的一组点，我们有Q⊆$\Delta T^w$。在本文的其余部分，我们使用D∈Q表示数据记录D在查询Q，并使用D/∈Q描述外部查询问注意，如果一个点的边界查询，它被视为一个内部点。我们使用$D_Q$来表示数据集D中几何范围查询Q内的数据记录集。

定义1(对称键GRSE)：对称键几何范围搜索加密是四种多项式时间算法=(GenKey，Enc，搜索)的元组，这样：

• SK←GenKey（1λ）：是一种概率密钥生成算法，由数据所有者运行来设置方案。它以一个安全参数λ作为输入，并输出一个密钥SK
• C←Enc(SK，D)：是一种由数据所有者运行的概率（或确定性）算法，用于加密一组数据记录。它以一个密钥SK和一个数据集D={D1，…，Dn}作为输入，其中$D_i\in \Delta T^w$，对于1≤i<=n。并输出一个加密的数据集C={C1，…，Cn}
• TK←GenToken(SK，Q)：是由数据所有者运行的一种概率（或确定性）算法来生成一个搜索令牌。它以一个密钥SK和一个几何范围查询Q作为输入，其中$Q\subseteq \Delta T^w$，并输出一个搜索令牌TK。
• IQ←Search(TK，C)：是一种由服务器运行的搜索加密数据的确定性算法。它以一个搜索令牌TK和一个加密的数据集C作为输入，并返回一组标识符$I_Q$，其中$I_i$是数据记录$D_i$的标识符（例如，云服务器中的内存位置），如果相应的数据记录$D_i\in Q$，则返回$I_i\in I_Q$。

2)正确性：我们说上述对称键symmetric-key GRSE方案是正确的，如果对于所有λ∈N，所有SK输出by $GenKey(1^{\lambda })$, all $D_i\in \Delta T^w$, all C output by $Enc(SK,D)$, all $Q\subseteq \Delta T^w$, all TK output by $GenToken(SK,Q)$

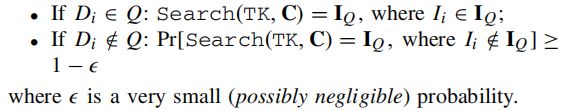
前面对对称密钥GRSE的描述默认是概率性的，如果Enc和GenToken都是确定性的，那么它就是确定性的。上述对称密钥GRSE的正确性表明，如果数据记录Di在查询Q内，则云服务器将返回相应的密文Ci；否则，云服务器将只以很小（可能可以忽略）的概率返回相应的密文Ci。上述描述不涉及任何数据结构，这意味着数据记录是逐个加密的，并且对加密的数据的搜索是根据加密的数据记录的数量线性地执行的。稍后我们将看到具有树状结构的高级设计.

PRELIMINARIES

Bloom Filters

Bloom滤波器是一种具有空间效率的概率数据结构，可用于测试元素是否为集合的成员。更具体地说，它能够表示一个元素肯定不在集合中，或者可能在集合中。换句话说，有假阳性，但没有假阴性。Bloom滤波器本质上是m位的位数组，其中BF=(b1，…，bm)，所有m位最初为空Bloom滤波器设置为0s。还有k个哈希函数hi，对于1≤i≤k(注意，非加密哈希函数对于实现Bloom过滤器就足够了)。

我们将上述两种算法表示为BF.ADD和BF.Test。每个操作的运行时间为O(k)，它与集合中的元素的数量无关。图4中描述了Bloom滤波器的一个例子

2）假阳性False Positives：Bloom滤波器BF的假阳性概率计算为
$P_{fp}[BF]={\left(1-{\left(1-\frac{1}{m}\right)}^{kt}\right)}^k\approx {\left(1-e^{-kt/m}\right)}^k$
其中t是被添加到Bloom过滤器中的元素数，m是Bloom过滤器的长度，k是哈希函数的个数。对这种假阳性的进一步分析可以在[47]中发现。上述概率随t的增加而增加，并随m的增加而减小。
3) 交集Intersection：另一个有趣而重要的特性是，两个集合的交集的布鲁姆过滤器可以用两个相应的布鲁姆过滤器的位运算近似计算，其中这两个布鲁姆过滤器有相同的长度m，用相同的哈希函数计算。具体地说，通过对两个Bloom滤波器BFS1和BFS2的位差计算，可以近似地得到S1和S2交点的Bloom滤波器
$$B{F}_{S_1\cap S_2}^{\wedge }=B{F}_{S_1}\bigwedge B{F}_{S_2}=\left(b_{1,1}\wedge b_{2,1},\dots ,b_{1,m}\wedge b_{2,m}\right)$$
这个按位组合的Bloom滤波器$B{F}_{S_1\cap S_2}^{\wedge }$将与一个$B{F}_{S1\cap S2}$大致相同，后者是基于S1∩S2[47]集从头构建的。在这个位组合Bloom滤波器中仍然没有假阴性，并且这个位组合Bloom滤波器的假阳性概率不大于BFS1或BFS2[47]的假阳性概率。这是因为$B{F}_{S_1\cap S_2}^{\wedge }$中的1位数不大于BFS1中的1位数或BFS2中的1位数。

Shen, Shi and Waters Encryption

Shen等人[30]提出了一种对称密钥概率函数加密(在本文中命名为SSW)，它能够在不揭示隐私的情况下测试两个向量的内积。具体来说，给定一个向量u和一个向量v，SSW能够在向量u上产生一个密文C，在向量v上产生一个标记TK。然后，只给定一个密文C和一个令牌TK，将输出对密文C和令牌TK的求值
$$\text{ SSW.Query }(TK,C)=1,\text{ iff }u\circ v=0$$
where $u\circ v=0$代表两个向量的内积。SSW是由双线性配对构建的，其安全性在选择性选择纯文攻击(IND-SCPA)下被正式定义为不可区分性。

据我们所知，SSW是最先进的功能加密，它是对称密钥，也评估内部乘积。最近的一些基于格和误差学习困难问题的功能加密Functional Encryption，可以比SSW更有效地评估两个向量的内积是否为0。然而，它是一种公钥方案，在匹配发生[49]时，它本质上无法实现查询隐私。换句话说，如何设计一个基于对称密钥格的功能加密支持内积仍然是一个有待解决的问题。因此，在下面的章节中，我们将利用SSW作为我们设计的构建块。另一方面，由于我们设计的兼容性，我们的方案不限于SSW。未来基于对称密钥晶格的功能加密使内部产品可以很容易地嵌入到我们的设计中，通过取代SSW作为构建块来进一步提高效率。

SYMMETRIC-KEY GRSE SCHEMES

Design Methodology

正如我们在第二节中所讨论的。对加密数据进行不同的连续操作，使得设计通用几何范围可搜索加密方案具有挑战性。为了灵活地管理不同的几何范围查询，本文的主要设计方法是在纯文本域中将每种类型的几何范围查询预处理为相同的形式，这样我们只需要处理密文域中单一类型的操作。因此，可以避免多轮客户机到服务器的交互或对多个非合并服务器的不切实际的假设。

更具体地说，正如我们在第二节中提到的。三，我们描述每个数据记录作为一个点，我们可以预处理每个几何范围查询作为一组点在数据空间（即，给定一个几何范围查询，很容易枚举所有可能的点在几何范围内与现有的明文领域，并表示这些可能的点作为一个集合）。例如，轴平行矩形内的所有可能点都可以很容易地通过两层循环枚举。具体来说，如果矩形的左下角为（5,10），左上角为（14,18），它其中的所有可能的点都可以枚举为

for (int i=5; i<=14; i++){
for (int j=10; j<=18; j++){
point[i,j];
} }

因此，对于密文域中的一般几何范围查询，我们基本上需要评估的关键操作是测试一个数据记录是否是一个集合的成员，该集合是由一个几何范围查询生成的。

A Deterministic Scheme

考虑到我们的设计方法，我们可以首先构建一个具有确定性加密（例如，伪随机函数[19]）和Bloom滤波器的基本方案。确定性加密的固有属性（即为相同的消息生成相同的密文）可以帮助我们对加密的数据一致地执行等式测试，并且使用Bloom过滤器可以提高集合成员测试的效率。

具体来说，数据所有者可以使用确定性加密来加密每个数据记录。而对于每个几何范围查询，在数据所有者枚举来自明文域中几何范围内的数据空间中的所有可能的点之后，它使用确定性加密分别加密所有这些可能的点，并将这些相应的密文添加到一个接一个的Bloom过滤器中。包含几何范围查询中所有可能点的密文的Bloom过滤器将被用作搜索令牌。最后，云服务器能够通过检查一个加密的数据记录是否是包含在Bloom过滤器中的一个元素来测试一个点是否在几何范围查询内。这个基本方案的一个例子如图6所示

该基本方案简单、有效。不幸的是，它只提供了非常有限的隐私保护。首先，由于它依赖于确定性加密，所以同一点的密文在加密的数据集中是相同的，并且在选择明文攻击下是不安全的。第二，因为布鲁姆过滤器（即搜索令牌）以明文形式向云服务器显示（即，服务器学习布鲁姆过滤器中哪个和多少位位置是1或0秒），所以云服务器根据布隆过滤器[47]的属性估计元素的数量是微不足道的。换句话说，如果两个几何范围查询的范围大小不同，那么对手要区分它们是微不足道的。我们将这种类型的泄漏表示为查询范围模式。除了Bloom过滤器之外，还可以利用其他常规集成员测试技术，如哈希表[50]。我们在这里特别使用布鲁姆滤波器，因为它是我们下一个概率设计的垫脚石

A Probabilistic Scheme

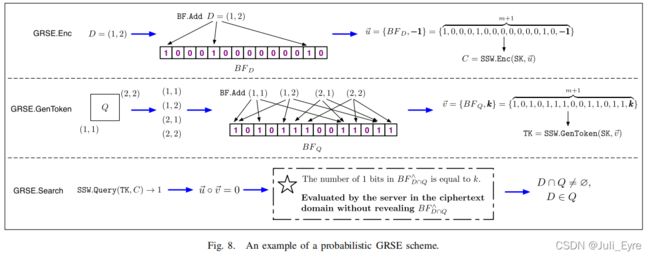
为了克服前面确定性方案的局限性，我们现在使用本节开头提到的相同设计方法构建一个概率GRSE方案。与确定性方案相比，该概率方案可以在IND-SCPA下提供数据隐私和查询隐私(见进一步的安全分析。vi)。此外，它还能够保留查询范围模式，这是上述确定性方案中不可避免的泄漏。为了实现这些安全目标，这个概率GRSE方案的主要区别（从高级级别）是首先在Bloom过滤器中添加点，然后利用概率加密Bloom过滤器中的所有位。

然而，使用概率加密来保护Bloom过滤器中的每一位都引入了验证set membership成员集的额外挑战。具体来说，由于概率加密自然会为同一消息产生不同的密文，因此服务器在计算上在Bloom过滤器中不可能区分哪些位是1s，哪些位是0s。因此，直接使用传统的方式(即BF.Test)来测试Bloom过滤器中在云端的元素的成员关系将不会提供有意义的搜索结果。因此，我们描述了另一种方法，称为Trick-1，来验证一个元素是否在布鲁姆滤波器的集合中，其中Trick-1是基于我们在Sec中提出的两个布loom滤波器的交集的属性。

1)Trick-1：给定一个元素x和一个Bloom过滤器$B{F}_S$，其中$B{F}_S$是基于一个集合S从头构建的，我们需要测试x是否是集合S的一个元素，其中S至少有一个元素(即，S不是null)。而不是直接计算x的哈希值，用BF.Test检查$B{F}_S$中的所有k个位置，我们创建了另一个只包含元素x的Bloom过滤器$B{F}_x$。然后，我们计算$B{F}_x$和$B{F}_S$上的按位and为
$$B{F}_{x\cap S}^{\wedge }=B{F}_x\wedge B{F}_S$$
其中，$B{F}_{x\cap S}^{\wedge }$是一个按位组合的Bloom滤波器，根据Sec中提出的Bloom滤波器的性质，近似表示x∩S的交集。然后，我们简单地计算$B{F}_{x\cap S}^{\wedge }$中的1位的数量。如果计算出Count=k，那么我们相信x是集合S中的一个元素（概率很高，见稍后的讨论）；否则，它肯定不是。

这个Trick-1的正确性依赖于这样一个事实，因为x是一个单个元素，它的Bloom滤波器$B{F}_x$恰好有k个1位。类似地，由于S至少有一个元素，它的Bloom过滤器$B{F}_S$将至少有k个1位。因此，根据位and的真值表，$B{F}_{x\cap S}^{\wedge }$最多可以有k个1位。同时，如果一个Bloom滤波器中的1位数小于k，那么它肯定不包含任何元素，这是微不足道的。因此，如果在$B{F}_{x\cap S}^{\wedge }$中计算Count=k，我们认为交集x∩S不是空的（概率很高）；否则，交点肯定为空。请注意，交点x∩S只有两种情况，其中它要么包含一个元素(即x)，要么什么都没有。因此，如果交点x∩S不是空的，则表示x在S的集合中(即，x∈S)；否则，它将显示x/∈S。

另一个重要的观察结果是，Count=k等价于说两个Bloom滤波器的内积是k。这个Trick-1并不像原来的方法那样简单(即BF.Test)，但在使用一些特殊的概率函数加密时，它对于评估加密数据上的元素的成员关系非常有用，特别是对于SSW[30]，它可以处理密文上的内积。

正如我们在第二节中提到的。这个按位组合的Bloom滤波器$B{F}_{x\cap S}^{\wedge }$与Bloom滤波器$B{F}_{x\cap S}$大致相同，这是从头开始计算出来的。由于这个原因，Trick-1在测试x是否在S的集合中时引入了假阳性。

FastGeo: Efficient Geometric Range Queries on Encrypted Spatial Data

在本文中，我们形式化了几何可搜索加密的概念，并提出了一个有效的方案，名为FastGeo，以保护在公共服务器上存储和查询的客户端空间数据集的隐私…FastGeo是一种新颖的加密空间数据的两级搜索，一个诚实但好奇的服务器可以有效地执行几何范围查询，并正确地将几何范围内的数据点返回给客户端，而不学习敏感数据点或此私有查询。FastGeo支持任意几何区域，实现次线性搜索时间，并允许在加密的空间数据集上进行动态更新。我们的方案被证明是安全的，我们在云平台上的真实空间数据集上的实验结果表明，FastGeo可以将搜索时间提高100倍以上

introduction

然而，如何使用亚线性搜索时间启用任意几何范围查询，同时支持对加密的空间数据的有效更新仍然是开放的。

与依赖于等式检查的关键字搜索和依赖于比较的范围搜索不同，在空间数据集上的几何范围查询基本上需要计算然后比较操作[11]。例如，为了确定一个点是否在一个圆内，我们计算从这个点到圆心的距离，然后将这个距离与这个圆的半径进行比较；为了验证一个点是否在一个多边形内，我们计算这个点与这个多边形的每个顶点的交叉积，并将每个交叉积与零（即正或负）[13]进行比较。

不幸的是，这种有效比较运算的要求使得支持几何范围查询的SE方案的设计更加具有挑战性，因为当前有效的密码原语不适合在密文中计算计算比较运算。更具体地说，伪随机函数(PRF)只能支持等式检查；保留顺序的加密[15]只支持比较；部分同态加密只能计算加法（或乘法）。BGN[17]计算加密数据的添加和最多一次乘法。另一方面，完全同态加密(FHE)[18]原则上可以安全地评估计算然后比较操作。然而，使用FHE的评估并不能直接揭示对加密数据的搜索决策（如内部或外部），这限制了它在搜索中的使用。

在本文中，我们形式化了几何可搜索加密(GSE)的概念，它是由SE方案的定义演变而来的，但侧重于几何查询。我们提出了一种名为FastGeo的GSE方案，它可以有效地检索几何区域内的点，而无需向诚实但好奇的服务器揭示私有数据点或敏感的几何范围查询。而不是直接评估计算比较操作，我们的主要思想是将空间数据和几何范围查询转换为一个新的形式，表示为平等向量形式，并利用两级搜索作为我们的关键解决方案来验证一个点是否在几何范围内， where the first level
securely operates equality checking with PRF and the second level privately evaluates inner products with Shen-ShiWaters encryption (SSW)。本文的主要贡献总结如下：

• 通过在我们的两级搜索中嵌入一个哈希表和一组链接列表作为空间数据的新结构，FastGeo可以实现次线性搜索，并支持任意几何范围（如圆和多边形）。与最近的解决方案相比，FastGeo不仅提供了对加密空间数据的高效更新，而且还提高了超过100倍的搜索性能。
• 我们形式化了GSE及其泄漏函数的定义，并严格证明了在选择性选择明文攻击(IND-SCPA)下的数据隐私和查询隐私具有不可区分性。
• 我们在云平台(AmazonEC2)中实现并评估了FastGeo，并证明了FastGeo在真实世界的空间数据集上是高效的。例如，一个超过49,870个加密元组的几何范围查询可以在15秒内执行，而一个更新平均只需要少于1秒。

RELATED WORK

OPE和一些支持比较的SE方案可以通过应用多个维度来执行矩形范围查询。然而，这些扩展不能用于其他几何范围区域，例如，一般的圆和多边形。Wang等人[9]提出了一种方案，特别是通过使用一组同心圆在加密数据上检索圆内的点。Zhu等人[10]还建立了一个加密空间数据的循环范围搜索方案。不幸的是，这两种方案只适用于圆，而不适用于其他几何区域。

日本田和Rughinis[8]设计了一个方案，通过使用隐藏向量加密[21]支持几何范围查询。它没有用$T^2$位的二进制向量编码一个点，其中T是维数大小，而是利用了一个分层编码，它将向量长度减少到2log2T位。然而，它的搜索时间仍然与数据集中的元组数量有关是线性的，这不仅在大规模数据集上运行缓慢，而且禁用了有效的更新。

我们最近的工作提出了一个可以操作任意几何范围查询的方案。它利用布鲁姆过滤器[23]及其属性，数据点表示为一个布鲁姆过滤器，几何范围查询也形成一个布鲁姆过滤器，和这两个布鲁姆过滤器的结果正确指示点是否在一个几何区域。它的高级版本与r-trees[24]平均可以实现对数搜索。虽然它也利用SSW作为构建块之一，但其基于树的索引和独特的Bloom过滤器的设计与本文介绍的新型两级索引完全不同，这些显著的差异阻止了之前的方案支持有效的更新和实际的搜索时间。

其他一些作品研究双方(如Alice和Bob)之间的安全几何运算，其中爱丽丝持有一个秘密点，Bob保持一个私有的几何范围。通过安全多方计算(SMC)，Alice和Bob可以决定一个点是否在几何范围内，而不向彼此透露秘密。然而，这些研究的模型与我们的模型不同(即，Alice和Bob都提供单独的私有输入，而我们模型中的客户机拥有所有的私有输入，但服务器没有私有输入)。此外，SMC还引入了广泛的交互作用。

PROBLEM STATEMENT

系统模型
在我们的模型中，有两个实体，包括一个客户端和一个服务器（在图1中）。客户端是一个将其空间数据集存储在服务器上的公司或组织。空间数据集中的每个元组本质上都是一个点。此外，它还希望对其外包的空间数据集执行几何范围查询。几何范围查询的目的是检索此几何范围内的点。该服务器由云服务提供商操作，并提供数据存储和查询处理服务。通过利用这些数据服务，客户机可以降低其本地成本。

服务器是诚实但很好奇的，它提供数据服务，但它很好奇，并试图揭示客户机的空间数据（即存储了哪些点）或几何范围查询（即搜索了哪些查询）。因此，客户端在将其空间数据集和几何范围查询处理到服务器之前，会对它们进行加密。只有客户端本身具有用于加密/解密的秘密密钥。同时，服务器需要对加密的空间数据正确地执行几何范围搜索而不进行解密，并将搜索结果（即几何范围查询内的点的密文）返回给客户端

定义1（GSE的定义）。一种几何可搜索的加密包括五种多项式时间算法：

In the above definition, each tuple $D_i$, for $i\in [1,n]$, in a spatial dataset $\mathbf{D}$ is a point of a data space ${\Delta }_T^{\alpha }$, where $\alpha$ denotes the number of dimensions and $T$ is the size of each dimension. We assume each dimension has the same size, and its range is from $[0,T-1]$. Without loss of generality, we also assume $\alpha =2$, then each point can be described as $D_i=\left(d_{i,1},d_{i,2}\right)$, where $d_{i,1}$ and $d_{i,2}$ are the values of this point in $\mathrm{x}$-dimension and $\mathrm{y}$-dimension respectively, and $d_{i,1},d_{i,2}\in [0,T-1]$. A geometric range query $Q$ is a range within the data space, which can be represented as $Q\subseteq {\Delta }_T^{\alpha }$. If a point $D_i$ is inside a query $Q$, we denote it as $D_i\in Q$; otherwise, we have $D_i\notin Q$.

这个定义是一个对称密钥GSE，因为索引的加密和搜索令牌的生成都使用相同的密钥。GSE方案的目标是构建空间数据集的加密索引，以便启用密文中的搜索功能，并最终输出一组标识符，指示与查询关联的加密点。有了这些标识符，服务器可以返回相应的加密点，客户端可以通过在本地解密加密的点来学习明文搜索结果。每个元组本身的加密和解密可以通过另一层额外的标准cpa安全加密(例如，AES-CBC-256)来传递，这在可搜索的加密中可以被忽略。GSE方案的正确性如下所示：

Definition 2 (Correctness of GSE). We say a GSE scheme $\Pi$ is correct if for all $\lambda \in \mathbb{N}$, all sk output by $\mathrm{GenKey}\left(1^{\lambda }\right)$, all $D_i\in {\Delta }_T^{\alpha }$, all $\Gamma$ output by Buildlndex $(\mathbf{D},\sigma )$, all ${\Gamma }^{\ast }$ output by $\mathrm{Enc}(\Gamma ,sk)$, all $Q\subseteq {\Delta }_T^{\alpha }$, and all tk output by GenToken $(Q,sk,\sigma )$, we have

• If $D_i\in Q:$ Query $\left({\Gamma }^{\ast },t{k}_Q\right)={\mathbf{I}}_Q$, where $I_i\in {\mathbf{I}}_Q$;
• If $D_i\notin Q:\mathrm{Pr}[\mathbf{Query}\left({\Gamma }^{\ast },t{k}_Q\right)={\mathbf{I}}_Q$, where $I_i\notin {\mathbf{I}}_Q]\ge$ $1-\mathrm{negl}(\lambda )$
  where $\mathrm{negl}(\lambda )$ is a negligible function [14] in terms of $\lambda$.

这种正确性意味着，该方案肯定会返回一个元组Di的密文的标识符如果这个点在查询Q内；如果这个点在查询Q之外，则将返回一个可以忽略的概率（即一个非常小的概率，在实际中可以被摄取）

安全目标
GSE的安全性是防止服务器学习空间数据和几何查询，同时支持几何范围搜索。具体来说，服务器不应该学习数据点的内容，也不能显示多边形的顶点或客户端正在搜索的圆的中心和半径。另一方面，允许服务器获得关于空间数据集的某些信息，以便高效地和功能性地操作查询。例如，服务器学习空间数据集中的元组总数（即大小模式）；它揭示了哪些标识符被搜索令牌触摸或检索（即访问模式）。这些泄漏可以正式地包含在泄漏函数L[2]中。我们将首先用这个泄漏函数证明我们在选择性选择明文攻击下的安全性，然后通过考虑一个更强的进行统计攻击的攻击者来进一步分析我们的隐私。细节将在第6节中描述。

PRELIMINARIES

通过利用PRF，我们可以对加密的数据执行等式检查。具体来说，给定两个消息m0和m1，它们的输出[m0]=[m1]，是相同的，当且仅当m0=m1。我们使用Init表示在PRF中初始化随机密钥的算法，并利用GetBits表示算法得到伪随机输出。
Shen-Shi-Waters Encryption. SSW [19] can evaluate whether the inner product of two vectors is zero without leaking privacy. Concretely, given two vectors $u=\left(u_1,\dots ,u_m\right)$ and $v=\left(v_1,\dots ,v_m\right)$, SSW generates a ciphertext $[u]$ with vector $u$ and a token $[v]$ with vector $v$. The evaluation on $[u]$ and $[v]$ indicates whether the inner product of $u$ and $v$ is zero as
$$\{\begin{array}{l}\text{ if }<u,v>=0,\mathrm{SSW}\cdot \text{ Query }([u],[v])=1\\ \text{ otherwise, }\mathrm{Pr}[\mathrm{SSW}\text{ Query }([u],[v])=0]\ge 1-\mathrm{negl}(\lambda ),\end{array}$$
without revealing vector $u$ nor $v$, where $<u,v>={\sum }_{i=1}^m{u}_i\cdot v_i$ is the inner product of two vectors. Its security can be proved with indistinguishability under Selective ChosenPlaintext Attacks [19], and the algorithms of SSW are briefly presented as below:

• $\mathrm{Setup}\left(1^{\lambda }\right)$ : Given a security parameter $\lambda$, output a secret key sk.
• $\mathrm{Enc}(sk,u)$ : Given $sk$ and a vector $u$, where $u=\left(u_1,\dots ,u_m\right)$, output a ciphertext $[u]$.
• GenToken $(sk,v)$ : Given $sk$ and a vector $v$, where $v=\left(v_1,\dots ,v_m\right)$, output a token $[v]$.
• Query $([u],[v])$ : Given ciphertext $[u]$ and token $[v]$, output 1 if $⟨u,v⟩=0$ and output 0 otherwise.
  The encryption time and token generation time are both $O(m)$, and the size of a ciphertext and the size of a token are also both $O(m)$, where $m$ is the vector length.

FASTGEO: AN EFFICIENT GSE

一个简单的设计不是直接运行计算然后比较操作，而是将计算然后比较操作分为两个步骤，其中服务器使用BGN对加密的数据进行计算（例如，计算一个距离），然后客户端在本地以明文方式进行比较。然而，客户端的大量本地解密将严重限制搜索性能。此外，通信开销相当于下载整个数据集，这显然并不实用。
Overview of FastGeo Design。为了克服这些限制，我们将几何范围查询和数据点转换为不同的形式，表示为等式向量形式，这样一起执行等式检查和计算内积可以正确有效地回答任意几何范围查询。为了在实现高效评估的同时仍然保持强大的隐私保证，我们利用PRF安全地实现平等检查，并利用SSW私下验证内积是否为零。此外，我们还将一个字典（实现为一个哈希表）与使用PRF相结合来实现次线性搜索。从高级层次来看，我们的设计可以解释为两级搜索，其中第一级依赖于相等检查，第二级依赖于评估内部乘积。此外，链接列表被应用于第二级，以支持有效的更新。

Data and Queries in Equality-Vector Form

我们使用一组示例来展示如何将数据和查询转换为等式向量形式（明文形式），这样计算然后比较操作就可以用等式检查和内积的组合来替换。同时，我们还演示了如何嵌入一个字典和一组链接列表来索引一个空间数据集。
如下图，we have a spatial dataset with five data points and a triangular range query $Q$. We assume the data space in this example is ${\Delta }_{10}^2$, i.e., two dimensions and each has a size of $T=10$, where $x\in [0,9]$ and $y\in [0,9]$. Only integers are considered in this example. 在不失一般性的情况下，这里以一个三角形为例。其他的几何对象，如圆形和矩形，也可以兼容。

基于这些数据点在x维中的不同值，我们首先构建一个字典(如图3所示)，字典中的每个元素都包含一个不同的x值。对于每个元素，我们还创建一个链接列表来表示其相应的y值，链接列表中的每个节点存储一个y值。显然，每个链接列表的大小取决于给定x值的数据点数量。例如，给定x = 6，有两个数据点(6,2)和(6,4)，则其链表的大小为2。此外，我们还会使用置换函数来保证每个列表中的节点是随机排列的。然后，我们将每个链表中的每个y值表示为一个向量，其中每个向量的长度为10(因为T = 10)。具体来说，如果y = i，那么向量中第i个分量设为1，而其他分量都赋值为0。组件的索引从0开始，以9结束。例如，y = 3，它的向量是(0,0,0,1,0,0,0,0,0)，其中只有下标3处的分量是1。

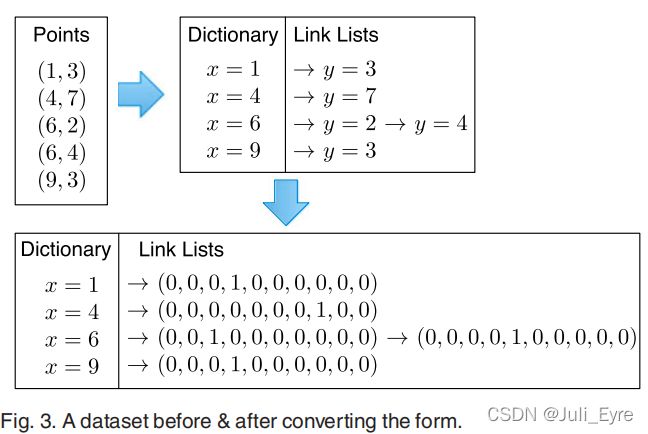
图2中给定一个几何范围查询Q，我们首先枚举这个几何范围查询内的所有可能的点（数据空间的）集合，并使用这个集合来表示几何范围查询。注意，这个枚举步骤对于明文[12]中的任何几何范围，都是简单的。接下来，我们根据这些可能点的x值生成一组x子查询，并为每个给定的x子查询计算一个y子查询，以覆盖所有这些可能的点（在图4中）。具体来说，每个x子查询仍然基于一个不同的x值，但我们使用一个向量来表示每个y子查询，其中向量中索引i处的分量被设置为0，如果

$y=i$ is covered by this geometric range query for a given $x$. For instance, when $x=6,y\in [1,2]$ is covered by $Q$, therefore, its corresponding $\mathrm{y}$-subquery in the vector format is $(1,0,0,1,1,1,1,1,1,1)$, where components from index 1 to index 2 are set as $0\mathrm{s}$ and others are $1\mathrm{s}$.

Search with Equality-Vector Form

使用这种等式向量形式，我们仍然可以正确地操作几何范围查询。具体来说，给定查询Q，我们首先在字典中搜索每个x子查询。一旦我们用x找到了一个匹配项，我们将继续计算它的y-子查询与对应的链接列表中的一个节点的内积。如果此内积为0，则表示数据点在几何范围查询内。例如，如图5所示，x=5和x=7作为x子查询通过等式检查不在字典内；一旦我们使用x=6在字典中找到匹配的项，我们继续使用它的y子查询来计算x=6链接列表中的每个节点的内积。本质上，我们也可以把我们的搜索过程看作是一个扫频算法，它一个接一个地扫频所有相关的x值（即垂直线）。扫频算法通常用于空间数据的计算几何中

Apply Encryption Primitives

通过这种等式向量形式的搜索，我们可以将PRF应用于等式部分（即第一级），并将SSW应用于数据和查询的向量部分（即第二级），以保护隐私，同时启用几何范围搜索的功能。此外，每个查询都应该实现一个具有新随机量的排列函数[14]，这样对每个查询中加密的一级值的扫描将遵循随机顺序。
The use of PRF, SSW and a permutation function with equality-vector form can fulfill search functionality and initial security, but another significant issue should still be solved. Specifically, the generation of a $x$-subquery and its corresponding $\mathrm{y}$-subquery are independent, where a curious server could freely change the search ability of a given query to another one by mismatching different encrypted $x$-subqueries with different encrypted y-subqueries (i.e., using an encrypted y-subquery $\left[v_i\right]$ for a different encrypted $\mathrm{x}$-subquery $\left[x_j\right]$, where $i\ne j)$. For instance, given a search token $t{k}_Q=\left\{\left\{\left[x_1\right],\left[v_1\right]\right\},\left\{\left[x_2\right],\left[v_2\right]\right\}\right\}$ of a geometric range query $Q$, the server could mismatch and query it as
$$t{k}_{Q^{\prime }}=\left\{\left\{\left[x_1\right],\left[v_2\right]\right\},\left\{\left[x_2\right],\left[v_1\right]\right\}\right\},$$
这可能泄漏不同的访问模式(例如，与使用原始搜索令牌$t{k}_Q$相比，可以检索不同的加密数据点)。这类问题在以前的一些SE方案中也被称为代牌勾结token collusion

为了防止令牌串通，我们提出了一种增强的向量形式，其中加密的y子查询只能用其加密的x子查询正确评估，而用其他x子查询不能。这种增强的思想是将一级值嵌入到第二级值的向量形式中。生成增强向量的算法如图6所示。例如，给定一个数据点(6,2)，其在增强向量形式下的y值为
$$u_e=(0,0,H(6),0,0,0,0,0,0,0,-1).$$
Correspondingly, given an $x$-subquery $x=6$ and its $y$-subquery $y\in [1,2]$, its $y$-subquery is
$$v_e=(0,1,1,0,0,0,0,0,0,0,H(6)).$$
It is obvious to see that the inner product of the two enhanced vectors $u_e$ and $v_e$ is zero if and only if the inner product of the two original vectors $u$ and $v$ is zero.