矩阵的ldu分解_【百川小课堂】第7课—详细图文讲解矩阵分解
点击“百川录”关注,获取更多精彩内容

最近百川在看SVD分解,找到一篇知乎推文介绍矩阵分解说的很棒的,特此分享给大家,相信大家看完都会有收获,文章来自知乎“史博”。
链接地址:https://zhuanlan.zhihu.com/p/52984150
百川修改了原文中关于SVD分解中两个正交矩阵的维度问题,原文此处有争议。
矩阵乘法分解
1. 基础知识点
对角和三角矩阵
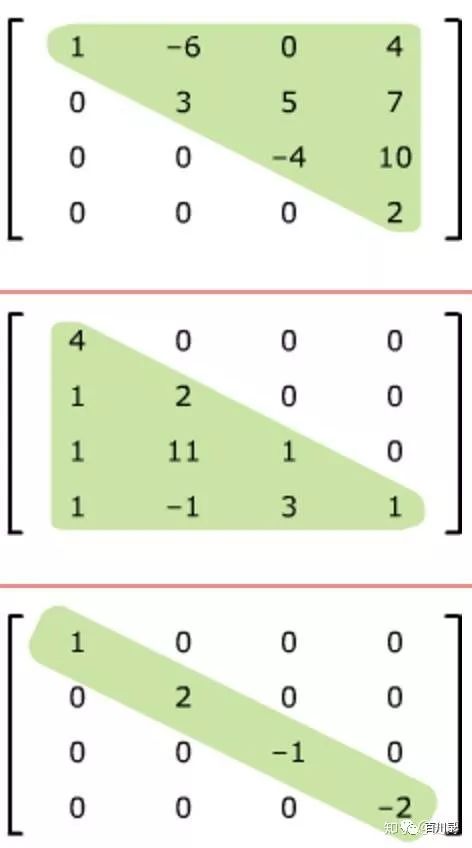
首先, 我们总结下, 在矩阵加法分解中出现了三种矩阵:上三角矩阵, 下三角矩阵 和 对角阵。这三种矩阵在乘法的分解中也会遇到。
正交矩阵
还有一种经典的矩阵, 叫正交矩阵, 什么叫正交矩阵呢?其实某种意义上, 正交矩阵也是通过矩阵乘法来定义的。如果一个矩阵和它的转置矩阵的乘积为单位矩阵, 那么这个矩阵就是正交矩阵。
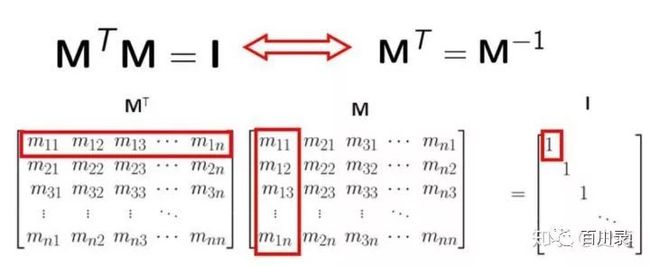
有了正交矩阵之后, 很容易得到一个结论就是正交矩阵的转置就是它的逆矩阵。
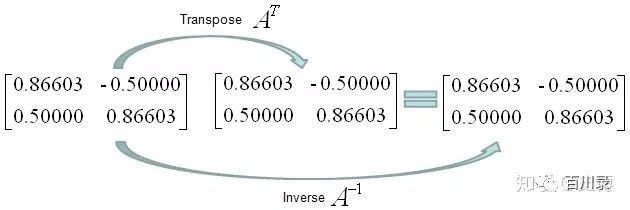
那么很容易就知道, 单位矩阵本身就是正交矩阵。

为什么叫正交矩阵呢?因为如果我们把这个矩阵写成向量的形式, 那么这些向量除了自己和自己的点积为1, 其他任意两个不同向量之间的点积全部为0. 而向量点积为0的情况叫正交。正交矩阵是因此得名的。
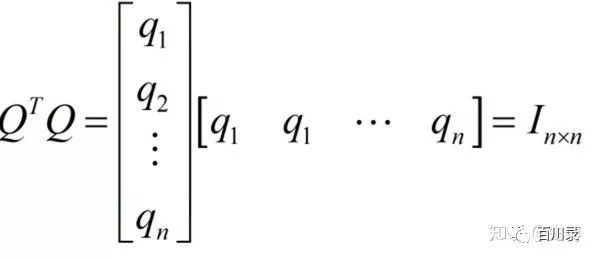
为什么要讲正交矩阵呢?还记得在矩阵的加法分解里面, 有求逆矩阵的情况么?试想一下,如果不要求逆矩阵了, 而是求解转置矩阵的话, 那是不是异常方便?对的, 这就是正交矩阵的强大的优势。
那么, 常见的LU, LDL, QR,SVD分解到底是什么?我们已经知道, 首先他们全是乘法分解。
2.常见乘法分解
LU分解
LU分解, 故名思议就是, 把矩阵分成下三角矩阵(Lower)和上三角矩阵(Upper)的一种分解。所以LU分解只用到了三角矩阵。
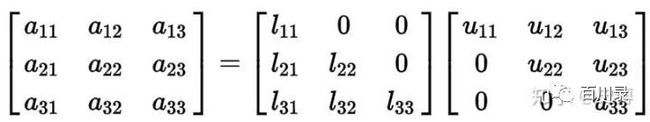
当然更进一步, 可以要求是一个稍微特殊点的三角矩阵, 就是下三角矩阵L对角线全1, 或者上三角矩阵U对角线元素全部为1.

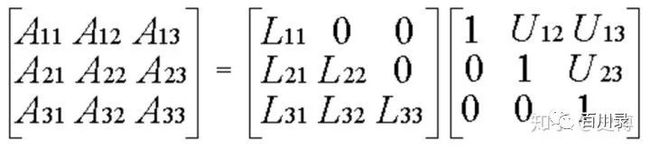
下面有个具体的例子, 大家可以试试:

LDU分解
在LU的基础上, 如果我们再进一步,引入对角矩阵(Diagonal)D, 那么LU分解就变成了LDU分解。是不是很直观?

而从LU分解到LDU分解是很容易做到的,只要把对角线的元素提取出来作为对角矩阵, 然后其他除以对角线元素进行等比例缩放。

这也很容易去解释, 为什么LU分解可以写成对角线全1的三角矩阵, 因为可以提取出一个对角矩阵, 然后乘到左边下三角矩阵或者右边上三角矩阵去。因此, 从本质上来说LDU分解和LU分解没有差别。所以常常把LDU分解忽略, 直接用LU分解来说明。
LDL分解
既然有了LDU分解, 那么LDL分解的字面上的意思就比较明确了, 就是下三角形L乘以对角矩阵, 再乘以下三角矩阵。对么?说对, 也对。说不对也不对。
我们来看一下, 其实最右边不是下三角矩阵,依然是上三角矩阵。但是这个上三角矩阵, 是最左边的下三角矩阵的转置, 所以依然是最左边的下三角矩阵。所以右边这个L的含义是左边的L的转置。

既然一个矩阵A能够这么分解, 那么我们知道A的转置和A是一样的, 因为LDL的转置刚好是它本身。

举个LDL的例子:

所以本质上来看, 对称矩阵的LDL分解就是LDU分解的一种特例。那么前面我们提到, LDU分解是LU分解的另外一种表达。那么, 对称矩阵也可以进行LL分解的。
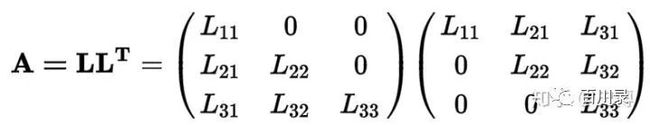
对应到上面的例子:
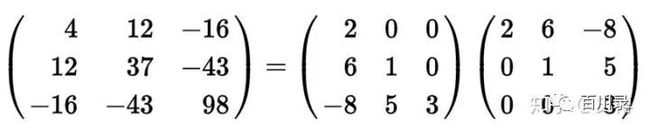
LDL 和LL分解合起来称为乔里斯基分解Cholesky decomposition。它是由法国数学家Cholesky发明的。
那么哪里去找到对称矩阵呢?其实很多时候, 是用来对(A^T)A进行分解的。

我们知道协方差矩阵就是经常写成(A^T)A这种形式,因此LDL和LL分解在相关性分析里面经常使用。
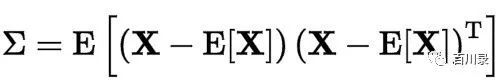
另外一个Cholesky分解的特点就是, 因为它的元素的对称性限制, 所以计算起来更快!
QR分解
前面的分解都没有用到正交矩阵, 而QR分解和SVD分解就要利用到正交矩阵。Q是一个正交矩阵, 而R是一个上三角矩阵。

前面我们提到单位矩阵也是正交矩阵, 所以正交矩阵可以看成是坐标系的转换。所以有时候, QR分解也可以表示成如下形式。

所以QR分解,是正交矩阵和三角矩阵的乘法分解。
SVD分解
SVD分解称为Singular value decomposition奇异值分解, 它是正交矩阵和对角矩阵的乘法分解。
所以, 从形式上, SVD可以表示成如下:
和 是单位正交阵

SVD与特征值分解联系参考:https://zhuanlan.zhihu.com/p/36538284 https://www.cnblogs.com/endlesscoding/p/10033527.html
乘法分解的形式小结
所以乘法分解就是把矩阵表示称为三角阵, 对角阵, 和正交矩阵的。
其中:
LU, LL是分解为三角矩阵的乘法
LDU, LDL 是分解为三角矩阵、和对角矩阵的乘法
QR 是分解为正交矩阵和三角矩阵的乘法
SVD 是分解为正交矩阵 和 对角矩阵的乘法
如果把三角矩阵、对角矩阵 和 正交矩阵称为因子矩阵, 为什么要分解成这些因子矩阵呢?
3.因子矩阵的几何含义
对角矩阵
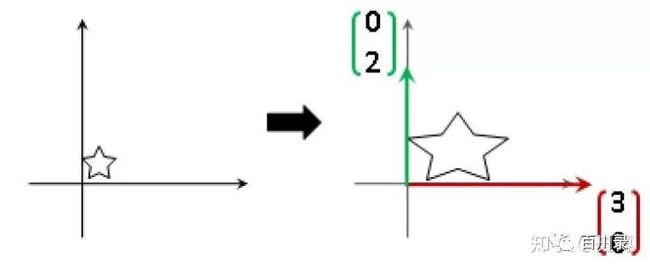
乘以一个对角矩阵,好比对每个坐标轴进行缩放!

正数的乘法:正数好比在原方向上的缩放, 大于1,表示伸长, 小于1,表示缩小。


负数的乘法:负数表示反反向。

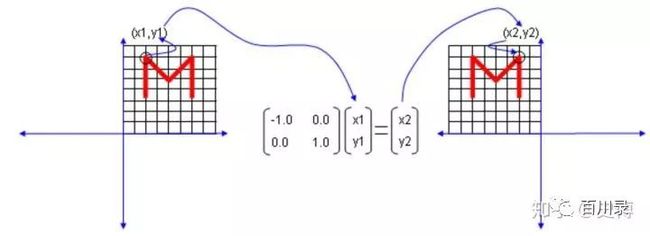


零的乘法:零表示空间压缩。

所以, 对角矩阵就是缩放,包括方向,和压缩。
三角矩阵
和对角矩阵相比, 三角矩阵要多一些角上的元素, 那么这些元素有什么作用呢?
上三角矩阵:上三角矩阵的作用好比进行右上的切变, 水平的斜拉。

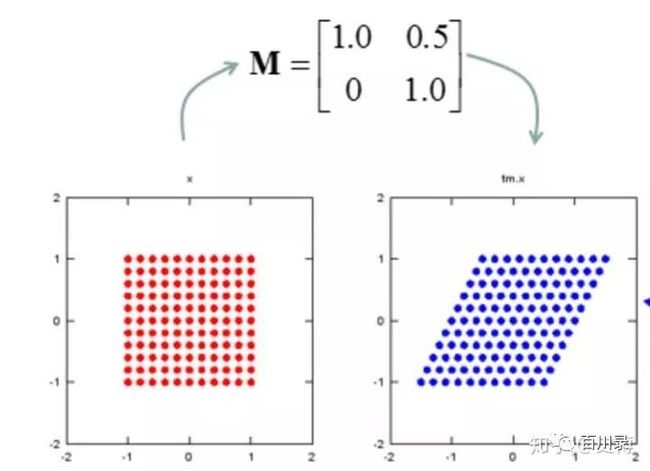


下三角矩阵:同样是切边, 不过是往左下切边, 垂直方向的下拉。
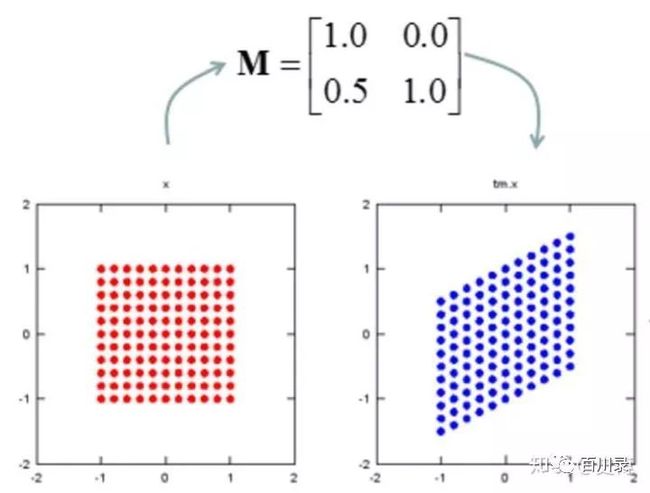


所以三角矩阵的作用就是切变。
正交矩阵
类似的, 我们可以看一下正交矩阵的作用, 我们可以利用一个正交矩阵, 找到对应乘法后的点的变化。
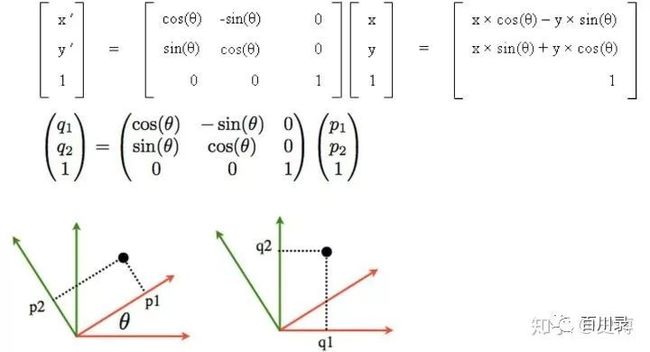
我们可以看到正交矩阵, 并不改变物体的形状, 但是进行了旋转。


4. 矩阵分解的几何意义
综上所述, 矩阵因子的作用就是要把缩放, 切边, 和旋转分解出来理解一个矩阵的作用。
在这种情况下, 矩阵乘法的分解就是连续进行几次变化的综合!

我们知道LU/LDU/LL/LDL分解和QR/SVD分解里面, 都有三角阵部分。那么三角阵到底有什么优势呢?
三角阵进行方程求解的优势
我们知道三角阵在进行高斯消元法的时候, 很容易进行化简, 逐层迭代进行计算求解。

所以三角阵除了有明确的几何含义,还有方程求解的极大便利性!这就是为什么三角阵这么受欢迎的原因!
LU分解的意义
LU分解使得矩阵AX=b的求解分成了LU两部分。

而三角矩阵的好处是可以很容易进行连续代入求解!这样可以先进行下三角矩阵的求解:

然后再进行上三角矩阵的求解。

这样能够快速进行求解。所以, LU分解把矩阵变成横向的切边和竖直方向的切变后, 能够带来计算上的极大的便利性。同时这种分解, 存储空间大小上几乎没有太多影响!

类似,我们可以理解LDU,LL, LDL的好处了。
QR分解的意义
从几何上QR分解,就是先进行旋转, 然后再进行切变的过程。

同时, 利用正交矩阵的旋转性, 可以同样很容易化解到三角矩阵乘法去求解。

这个过程中, 并不需要进行求逆运算, 只需要进行转置运算和乘法运算。然后就可以利用三角不等式逐层迭代求解的便利性。
SVD分解的意义
按照前面给出的几何含义, SVD 分解可以看成先旋转, 然后进行分别缩放, 然后再旋转的过程。

类似的, 同样计算上还带来了极大的便利性!
5.矩阵分解的应用
除了计算上带来的极大便利性, 分解因子的几何意义还使得矩阵乘法分解有其他很多应用。
相关性分析
LL相关的分析很容易就被用到相关性分析上去。

特征值和特征向量求解
SVD分解还可以用来做特征值和特征向量的求解。

-End-
分享人生,分享技术
我是百川,欢迎大家留言交流
觉得有收获,点个“在看”,转发到朋友圈
百川推荐
小课堂留言板