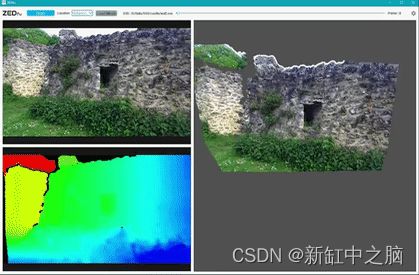
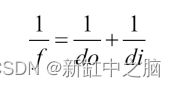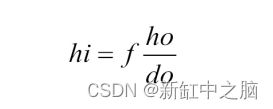基于双目视觉的三维重建C++实战

就在一年前，在我开始写这篇文章之前，我观看了特斯拉人工智能总监 Andrej Karapathy 的一次演讲，他向世界展示了特斯拉汽车如何使用连接到汽车上的摄像头感知深度、在 3D 中重建其周围环境并实时做出决策，一切（除了用于安全的前置雷达）都是通过视觉计算的。那个演讲让我大吃一惊！

当然，我知道可以通过摄像头对环境进行三维重建，但我的想法是，当我们拥有激光雷达、雷达等如此高精度的传感器时，为什么会有人冒险使用普通摄像头。用更少的计算量为我们提供准确的三维环境呈现？我开始研究（试图理解）与深度感知和视觉三维重建这一主题相关的论文，并得出结论，我们人类从来没有从我们的头脑中发出光线来感知我们周围的深度和环境，我们聪明，只用我们的两只眼睛就能感知周围环境，从开车或骑自行车从办公室到办公室，或者在世界上最危险的赛道上以 230 英里/小时的速度驾驶一级方程式赛车，我们从不需要激光来做出决定以微秒为单位。一旦我们解决了视觉问题，这些昂贵的传感器将变得毫无意义。

在视觉深度感知领域正在进行大量研究，特别是随着机器学习和深度学习的进步，我们现在能够仅从视觉以高精度计算深度。所以在我们开始学习概念和实现这些技术之前，让我们先看看这项技术目前处于什么阶段，以及它的应用是什么。

机器人视觉 - 使用 ZED 相机进行环境感知：

为自动驾驶创建高清地图 - 深度学习的深度感知：

SfM（基于运动的结构）和 SLAM（同时定位和映射）是我将在本教程中介绍的概念的主要技术之一，下图为LSD-SLAM 的演示。

现在我们已经有了足够的学习灵感，我将开始教程。因此，首先我将教你了解幕后发生的事情所需的基本概念，然后使用 C++ 中的 OpenCV 库应用它们。您可能会问的问题是，为什么我在 C++ 中实现这些概念，而在 python 中实现这些概念会容易得多，这背后是有原因的。第一个原因是 python 的速度不够快，无法实时实现这些概念，第二个原因是，与 python 不同，使用 C++ 会要求我们理解这些概念，否则无法实现。

在本教程中，我们将编写两个程序，一个是获取场景的深度图，另一个是获取场景的点云，均使用立体视觉。

在我们直接进入编码部分之前，了解相机几何的概念对我们来说很重要，我现在将教你。

1、相机模型

自摄影开始以来，用于生成图像的过程并没有改变。来自观察场景的光线由相机通过正面光圈（镜头）捕获，该光圈将光线射到位于相机镜头后部的图像平面上。该过程如下图所示：

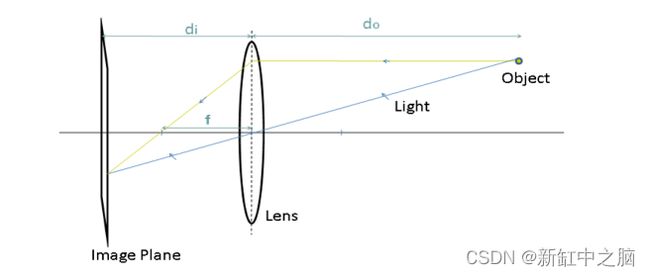
在上图中，do是镜头到被观察物体的距离，di是镜头到像平面的距离。f将因此成为镜头的焦距。这些描述的量之间存在所谓的“薄透镜方程”之间的关系，如下所示：

现在让我们看看现实世界中的 3 维对象如何投影到 2 维平面（照片）的过程。我们理解这一点的最好方法是看看相机是如何工作的。

相机可以被视为将 3-D 世界映射到 2-D 图像的功能。让我们以最简单的相机模型为例，即针孔相机模型，这是人类历史上较古老的摄影机制。下面是针孔摄像头的工作图：

从这张图我们可以得出：

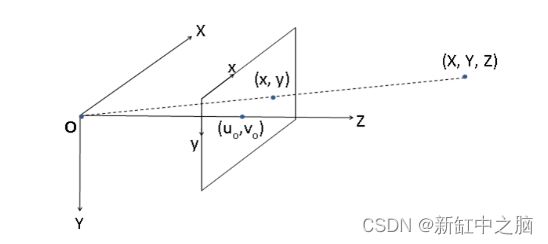
这里很自然地，由物体形成的图像的大小hi将与物体到相机的距离do成反比。此外，位于 (X, Y, Z) 位置的 3-D 场景点将投影到 (x,y) 处的图像平面上，其中 (x,y) = (fX/Z, fY/Z)。其中 Z 坐标是指点的深度，这在上一张图像中完成。整个相机配置和符号可以使用齐次坐标 系用一个简单的矩阵来描述。

当相机生成世界的投影图像时，投影几何被用作现实世界中物体几何、旋转和变换的代数表示。

齐次坐标是射影几何中使用的坐标系统。即使我们可以在欧几里得空间中表示现实世界中对象（或 3-D 空间中的任何点）的位置，但必须执行的任何变换或旋转都必须在齐次坐标空间中执行，然后再返回。让我们看看使用齐次坐标的优点：

• 涉及齐次坐标的公式通常比笛卡尔世界中的更简单。
• 无穷远处的点可以用有限坐标来表示。
• 单个矩阵可以代表相机和世界之间可能发生的所有可能的保护性转换。

在齐次坐标空间中，2-D点用3个向量表示，3-D点用4个向量表示：

在上述方程中，第一个带有f符号的矩阵称为内参矩阵（或俗称内参矩阵）。这里的内在矩阵现在只包含焦距（f），我们将在本教程之前研究这个矩阵的更多参数。

具有 r 和 t 符号的第二个矩阵称为外部参数矩阵（或通常称为外部矩阵）。该矩阵中的元素表示相机的旋转和平移参数（即相机在现实世界中的放置位置和方式）。

因此，这些内在和外在矩阵一起可以为我们提供图像中的 (x,y) 点和现实世界中的 (X, Y, Z) 点之间的关系。这就是根据给定相机的内在和外在参数将 3-D 场景点投影到 2-D 平面上的方式。

现在我们已经获得了关于射影几何和相机模型的足够知识，是时候介绍计算机视觉几何中最重要的元素之一——基本矩阵。

2、基础矩阵

现在我们知道了如何将 3-D 世界中的点投影到相机的图像平面上。我们将研究显示同一场景的两个图像之间存在的投影关系。当这两个相机被刚性基线分开时，我们使用术语立体视觉。考虑两个针孔相机观察一个给定的场景点共享相同的基线，如下图所示：

从上图中，世界点X的图像位于图像平面上的位置x，现在这个x可以位于 3-D 空间中这条线上的任何位置。这意味着如果我们想在另一幅图像中找到相同的点x，我们需要沿着这条线在第二幅图像上的投影进行搜索。

从x绘制的这条假想线称为x的极线。这条核线带来了一个基本的约束，即给定点的匹配在另一个视图中必须位于这条线上。这意味着如果你想从第二张图像中的第一张图像中找到x ，你必须沿着第二张图像上x的核线寻找它。这些极线可以表征两个视图之间的几何形状。这里要注意的重要一点是，所有核线总是通过一个点。该点对应于一个摄像机中心到另一台摄像机中心的投影，该点称为极点。

我们可以将基础矩阵F视为将一个视图中的二维图像点映射到另一个图像视图中的核线的矩阵。图像对之间的基本矩阵可以通过求解一组方程来估计，这些方程涉及两幅图像之间一定数量的已知匹配点。这种匹配的最小数量是七，最佳数量是八。然后对于一个图像中的一个点，基本矩阵给出了应该在另一个视图中找到其对应点的线的方程。

如果一个点(x,y)的一个点的对应点是(x’,y’)，并且两个图像平面之间的基本矩阵是F，那么我们在齐次坐标中一定有下面的方程：

这个方程表达了两个对应点之间的关系，称为对极约束。

3、使用 RANSAC 匹配图像点

当两个摄像机观察同一个场景时，它们看到的是相同的物体，但在不同的视点下。C++ 和 Python 中都有像 OpenCV 这样的库，它们为我们提供了特征检测器，它们可以在图像中找到带有描述符的某些点，他们认为这些点对图像来说是唯一的，如果给定同一场景的另一个图像，就可以找到这些点。然而，实际上并不能保证通过比较检测到的特征点的描述符（如 SIFT、ORB 等）在两幅图像之间获得的匹配集是准确和真实的。这就是为什么引入了基于RANSAC（随机采样共识）策略的基本矩阵估计方法。

RANSAC 背后的想法是从给定的一组数据点中随机选择一些数据点，并仅使用这些数据点进行估计。所选点的数量应该是估计数学实体所需的最小点数，在我们的基本矩阵的例子中是八个匹配。一旦从这八个随机匹配中估计出基本矩阵，匹配集中的所有其他匹配都将针对我们讨论的极线约束进行测试。这些匹配形成计算的基本矩阵的支持集。

支持集越大，计算出的矩阵是正确的概率就越高。如果随机选择的匹配之一是不正确的匹配，那么计算的基本矩阵也将是不正确的，并且其支持集预计会很小。这个过程重复多次，最后，具有最大支持集的矩阵将被保留为最可能的矩阵。

4、从立体图像计算深度图

人类进化成有两只眼睛的物种的原因是我们可以感知深度。当我们在机器中以类似的方式组织相机时，它被称为立体视觉。立体视觉系统通常由两个并排的摄像机组成，观察同一场景，下图显示了具有理想配置的立体设备的设置，完美对齐。

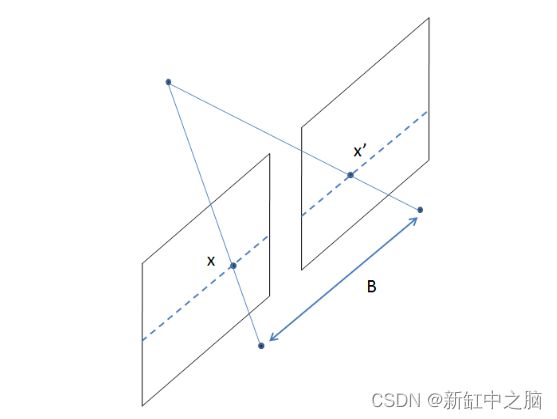
在如上图所示的相机理想配置下，相机仅通过水平平移分开，因此所有核线都是水平的。这意味着对应的点具有相同的y坐标，搜索减少到一维线。当相机被这样一个纯水平平移分开时，第二个相机的投影方程将变为：

通过查看下图，该等式会更有意义，这是数码相机的一般情况：

其中点(uo, vo)是通过镜头主点的线穿过像平面的像素位置。这里我们得到一个关系：

这里，术语(x-x’)称为视差，Z当然是深度。为了从立体对计算深度图，必须计算每个像素的视差。

但在现实世界中，获得这样一个理想的配置是非常困难的。即使我们准确地放置相机，它们也不可避免地会包含一些额外的过渡和旋转组件。

幸运的是，可以通过使用稳健的匹配算法来校正这些图像以生成所需的水平线，该算法利用基本矩阵来执行校正。

现在让我们从获得以下立体图像的基本矩阵开始：

可以通过单击此处从 GitHub 存储库下载上述图像。在开始编写本教程中的代码之前，请确保你的计算机上已构建 opencv 和 opencv-contrib 库。如果它们未构建，我建议你访问此链接以安装它们（ 仅针对Ubuntu ）。

5、编写实现代码

#include 
#include "opencv2/xfeatures2d.hpp"
using namespace std;
using namespace cv;
int main(){
cv::Mat img1, img2;
img1 = cv::imread("imR.png",cv::IMREAD_GRAYSCALE);
img2 = cv::imread("imL.png",cv::IMREAD_GRAYSCALE);

我们做的第一件事是包含来自 opencv 和 opencv-contrib 的所需库，我要求你在开始本节之前构建它们。在main()函数中，我们初始化了cv:Mat数据类型的两个变量，它是 opencv 库的成员函数，Mat数据类型可以通过动态分配内存来保存任意大小的向量，尤其是图像。然后使用cv::imread()我们将图像导入mat数据类型的img1和img2中。cv::IMREAD_GRAYSCALE参数将图像导入为灰度。

// Define keypoints vector
std::vector keypoints1, keypoints2;
// Define feature detector
cv::Ptr ptrFeature2D = cv::xfeatures2d::SIFT::create(74);
// Keypoint detection
ptrFeature2D->detect(img1,keypoints1);
ptrFeature2D->detect(img2,keypoints2);
// Extract the descriptor
cv::Mat descriptors1;
cv::Mat descriptors2;
ptrFeature2D->compute(img1,keypoints1,descriptors1);
ptrFeature2D->compute(img2,keypoints2,descriptors2);

在这里，我们使用 opencv 的 SIFT 特征检测器来从图像中提取所需的特征点。如果你想了解有关这些特征检测器如何工作的更多信息，请访问此链接。我们上面获得的描述符描述了提取的每个点，这个描述用于在另一个图像中找到它：

// Construction of the matcher
cv::BFMatcher matcher(cv::NORM_L2);
// Match the two image descriptors
std::vector outputMatches;
matcher.match(descriptors1,descriptors2, outputMatches);

BFMatcher获取第一组中一个特征的描述符，并使用一些阈值距离计算与第二组中的所有其他特征匹配，并返回最接近的一个。我们将 BFMatches 返回的所有匹配项存储在vectorcv::DMatch类型的输出匹配变量中。

// Convert keypoints into Point2f
std::vector points1, points2;
for (std::vector::const_iterator it=   outputMatches.begin(); it!= outputMatches.end(); ++it) {
    // Get the position of left keypoints
    points1.push_back(keypoints1[it->queryIdx].pt);
    // Get the position of right keypoints
    points2.push_back(keypoints2[it->trainIdx].pt);
     }

获取的关键点首先需要转换为cv::Point2f类型，以便与cv::findFundamentalMat一起使用，我们将使用该函数使用我们抽象的这些特征点来计算基本矩阵。两个结果向量Points1和Points2包含两个图像中的对应点坐标。

std::vector inliers(points1.size(),0);
cv::Mat fundamental= cv::findFundamentalMat(
  points1,points2, // matching points
     inliers,         // match status (inlier or outlier)  
     cv::FM_RANSAC,   // RANSAC method
     1.0,        // distance to epipolar line
     0.98);     // confidence probability
cout<

最后，我们调用了 cv::findFundamentalMat。

// Compute homographic rectification
cv::Mat h1, h2;
cv::stereoRectifyUncalibrated(points1, points2, fundamental,
 img1.size(), h1, h2);
// Rectify the images through warping
cv::Mat rectified1;
cv::warpPerspective(img1, rectified1, h1, img1.size());
cv::Mat rectified2;
cv::warpPerspective(img2, rectified2, h2, img1.size());

正如我之前在教程中解释的那样，在实际世界中，获得理想的相机配置而没有任何错误是非常困难的，因此 opencv 提供了一个校正功能，该功能应用单应变换将每个相机的图像平面投影到完美对齐的虚拟平面上. 这种变换是根据一组匹配点和基本矩阵计算得出的。

// Compute disparity
cv::Mat disparity;
cv::Ptr pStereo = cv::StereoSGBM::create(0,               32,5);
pStereo->compute(rectified1, rectified2, disparity);
cv::imwrite("disparity.jpg", disparity);

最后，我们计算了视差图。从下图中，较暗的像素代表离相机较近的物体，较亮的像素代表远离相机的物体。你在输出视差图中看到的白色像素噪声可以使用一些我不会在本教程中介绍的过滤器来去除。

现在我们已经成功地从给定的立体对中获得了深度图。现在让我们尝试使用 opencv 中名为 3D-Viz 的工具将获得的 2-D 图像点重新投影到 3-D 空间，该工具将帮助我们渲染 3-D 点云。

但是这一次，我们不是从给定的图像点估计一个基本矩阵，而是使用一个基本矩阵来投影这些点。

6、本质矩阵

本质矩阵可以看作是基础矩阵，但用于校准的相机。我们也可以将其称为对基础矩阵的专业化，其中矩阵是使用校准的相机计算的，这意味着我们必须首先获取有关我们在世界上的相机的知识。

因此，为了让我们估计本质矩阵，我们首先需要相机的内在矩阵（表示给定相机的光学中心和焦距的矩阵）。让我们看一下下面的等式：

这里，从第一个矩阵中，fx和fy代表相机的焦距，(uo, vo)是主点。这是内在矩阵，我们的目标是估计它。

这种寻找不同相机参数的过程称为相机校准。我们显然可以使用相机制造商提供的规格，但是对于我们将要做的 3-D 重建等任务，这些规格不够准确。因此，我们将执行我们自己的相机校准。

这个想法是向相机显示一组场景点，这些点我们知道它们在现实世界中的实际 3-D 位置，然后观察这些点在获得的图像平面上的投影位置。有了足够数量的 3-D 点和相关的 2-D 图像点，我们就可以从投影方程中抽象出精确的相机参数。

做到这一点的一种方法是从不同的视点拍摄一组世界的 3-D 点及其已知 3-D 位置的多张图像。我们将使用 opencv 的校准方法，其中一种方法将棋盘图像作为输入，并返回所有存在的角。我们可以自由假设板位于 Z=0，X 和 Y 轴与网格很好地对齐。我们将在下面的部分中了解 OpenCV 的这些校准功能是如何工作的。

7、三维场景重建

让我们首先创建三个函数，我们将在 main 函数中使用它们。这三个功能将

• addChessBoardPoints() //返回给定棋盘图像的角点
• calibrate() // 从提取的点返回内在矩阵
• triangulate() //返回重建点的 3-D 坐标

#include "CameraCalibrator.h"
#include 
#include "opencv2/xfeatures2d.hpp"
using namespace std;
using namespace cv;
std::vector rvecs, tvecs;
// Open chessboard images and extract corner points
int CameraCalibrator::addChessboardPoints(
         const std::vector& filelist, 
         cv::Size & boardSize) {
// the points on the chessboard
std::vector imageCorners;
std::vector objectCorners;
// 3D Scene Points:
// Initialize the chessboard corners 
// in the chessboard reference frame
// The corners are at 3D location (X,Y,Z)= (i,j,0)
for (int i=0; i

在上面的代码中，可以观察到我们包含了一个头文件“CameraCalibrator.h”，它将包含该文件的所有函数声明和变量初始化。可以通过访问此链接在我的 Github 上下载本教程中的标题以及所有其他文件。

我们的函数利用了 opencv 的findChessBoardCorners()函数，该函数将图像位置数组（数组必须包含每个棋盘图像的位置）和棋盘尺寸（你应该输入棋盘中水平和垂直角的数量）作为输入参数并返回给我们一个包含角点位置的向量。

double CameraCalibrator::calibrate(cv::Size &imageSize)
{
  // undistorter must be reinitialized
  mustInitUndistort= true;
// start calibration
  return 
     calibrateCamera(objectPoints, // the 3D points
          imagePoints,  // the image points
          imageSize,    // image size
          cameraMatrix, // output camera matrix
          distCoeffs,   // output distortion matrix
          rvecs, tvecs, // Rs, Ts 
          flag);        // set options
}

在这个函数中，我们使用了calibrateCamera()函数，它获取我们上面获得的 3-D 点和图像点，并返回给我们固有矩阵、旋转向量（描述相机相对于场景点的旋转）和平移矩阵（描述相机相对于场景点的位置）。

cv::Vec3d CameraCalibrator::triangulate(const cv::Mat &p1, const cv::Mat &p2, const cv::Vec2d &u1, const cv::Vec2d &u2) {
// system of equations assuming image=[u,v] and X=[x,y,z,1]
  // from u(p3.X)= p1.X and v(p3.X)=p2.X
  cv::Matx43d A(u1(0)*p1.at(2, 0) - p1.at(0, 0),
  u1(0)*p1.at(2, 1) - p1.at(0, 1),
  u1(0)*p1.at(2, 2) - p1.at(0, 2),
  u1(1)*p1.at(2, 0) - p1.at(1, 0),
  u1(1)*p1.at(2, 1) - p1.at(1, 1),
  u1(1)*p1.at(2, 2) - p1.at(1, 2),
  u2(0)*p2.at(2, 0) - p2.at(0, 0),
  u2(0)*p2.at(2, 1) - p2.at(0, 1),
  u2(0)*p2.at(2, 2) - p2.at(0, 2),
  u2(1)*p2.at(2, 0) - p2.at(1, 0),
  u2(1)*p2.at(2, 1) - p2.at(1, 1),
  u2(1)*p2.at(2, 2) - p2.at(1, 2));
cv::Matx41d B(p1.at(0, 3) - u1(0)*p1.at(2,3),
                p1.at(1, 3) - u1(1)*p1.at(2,3),
                p2.at(0, 3) - u2(0)*p2.at(2,3),
                p2.at(1, 3) - u2(1)*p2.at(2,3));
// X contains the 3D coordinate of the reconstructed point
  cv::Vec3d X;
  // solve AX=B
  cv::solve(A, B, X, cv::DECOMP_SVD);
  return X;
}

上述函数采用可以使用先前函数的固有矩阵获得的投影矩阵和归一化图像点，并返回上述点的 3-D 坐标。

下面是从立体对进行 3-D 重建的完整代码。此代码需要至少 25 到 30 张棋盘图像，这些图像来自你拍摄立体对图像的同一台相机。为了首先在你的 PC 中运行此代码，请克隆我的 GitHub 存储库，将双目对替换为自己的，并将棋盘图像位置数组替换为自己的数组，然后构建和编译。我正在将示例棋盘图像上传到我的 GitHub 以供你参考，你必须拍摄大约 30 张这样的图像并在代码中提及。

int main(){
cout<<"compiled"< files = {"boards/1.jpg"......};
  cv::Size board_size(7,7);
CameraCalibrator cal;
  cal.addChessboardPoints(files, board_size);
cv::Mat img = cv::imread("boards/1.jpg");
cv::Size img_size = img.size();
  cal.calibrate(img_size);
  cout< keypoints1;
  std::vector keypoints2;
  cv::Mat descriptors1, descriptors2;
// Construction of the SIFT feature detector
  cv::Ptr ptrFeature2D = cv::xfeatures2d::SIFT::create(10000);
// Detection of the SIFT features and associated descriptors
  ptrFeature2D->detectAndCompute(image1, cv::noArray(), keypoints1, descriptors1);
  ptrFeature2D->detectAndCompute(image2, cv::noArray(), keypoints2, descriptors2);
// Match the two image descriptors
  // Construction of the matcher with crosscheck
  cv::BFMatcher matcher(cv::NORM_L2, true);
  std::vector matches;
  matcher.match(descriptors1, descriptors2, matches);
cv::Mat matchImage;
cv::namedWindow("img1");
  cv::drawMatches(image1, keypoints1, image2, keypoints2, matches, matchImage, Scalar::all(-1), Scalar::all(-1), vector(), DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
  cv::imwrite("matches.jpg", matchImage);
// Convert keypoints into Point2f
  std::vector points1, points2;
for (std::vector::const_iterator it = matches.begin(); it != matches.end(); ++it) {
    // Get the position of left keypoints
    float x = keypoints1[it->queryIdx].pt.x;
    float y = keypoints1[it->queryIdx].pt.y;
    points1.push_back(cv::Point2f(x, y));
    // Get the position of right keypoints
    x = keypoints2[it->trainIdx].pt.x;
    y = keypoints2[it->trainIdx].pt.y;
    points2.push_back(cv::Point2f(x, y));
  }
// Find the essential between image 1 and image 2
  cv::Mat inliers;
  cv::Mat essential = cv::findEssentialMat(points1, points2, cameraMatrix, cv::RANSAC, 0.9, 1.0, inliers);
cout< inlierPts1;
  std::vector inlierPts2;
  // create inliers input point vector for triangulation
  int j(0);
  for (int i = 0; i < inliers.rows; i++) {
    if (inliers.at(i)) {
      inlierPts1.push_back(cv::Vec2d(points1[i].x, points1[i].y));
      inlierPts2.push_back(cv::Vec2d(points2[i].x, points2[i].y));
    }
  }
  // undistort and normalize the image points
  std::vector points1u;
  cv::undistortPoints(inlierPts1, points1u, cameraMatrix, distCoeffs);
  std::vector points2u;
  cv::undistortPoints(inlierPts2, points2u, cameraMatrix, distCoeffs);
// Triangulation
  std::vector points3D;
  cal.triangulate(projection1, projection2, points1u, points2u, points3D);
cout<<"3D points :"<

我知道 代码显示是一团糟，尤其是对于 C++，所以我建议你去我的GitHub并理解上面的代码。

对我来说，给定对的输出如下所示，可以通过调整特征检测器及其类型来改进。

任何有兴趣深入学习这些概念的人，我都会在下面推荐这本书，我认为这本书是计算机视觉几何的圣经。这也是本教程的参考书。

计算机视觉中的多视图几何第 2 版- Richard Hartley 和 Andrew Zisserman。

---

原文链接：三维重建C++实战 — BimAnt