门控循环单元（GRU）

入门小菜鸟，希望像做笔记记录自己学的东西，也希望能帮助到同样入门的人，更希望大佬们帮忙纠错啦~侵权立删。

✨完整代码在我的github上，有需要的朋友可以康康✨

​​​​​​https://github.com/tt-s-t/Deep-Learning.git

目录

一、背景

二、原理

1、前向传播

（1）重置门和更新门

（2）候选隐藏状态

（3）隐藏状态

（4）输出

2、反向传播

三、GRU的优缺点

1、优点

2、缺点

四、代码实现GRU

1、numpy实现GRU模型

（1）前期准备

（2）初始化参数

（3）前向传播

（4）后向传播

（5）预测

2、调用我们实现的GRU进行训练与预测

3、result

---

一、背景

       当时间步数(T)较大或时间步(t)较小的时候，RNN的梯度较容易出现衰减或爆炸。虽然裁剪梯度可以应对梯度爆炸，但是无法解决梯度衰减的问题。这个原因使得RNN在实际中难以捕捉时间序列中时间步(t)距离较大的依赖关系。因此LSTM应运而生，基于LSTM，改进出了GRU。

       RNN详解可以看看：RNN循环神经网络_tt丫的博客-CSDN博客_rnn应用领域

---

二、原理

1、前向传播

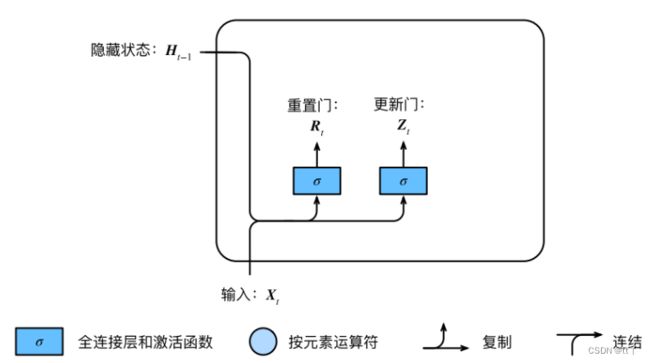
（1）重置门和更新门

两个门的输入都是当前时间步输入  与上一时间步的隐藏状态 。

（图片都来源于《动手学深度学习》）

 前向传播的计算为：

其中，

为激活函数（sigmoid函数），故取值范围为：[0,1]

n为样本数，d为输入的特征数，h为隐藏大小。

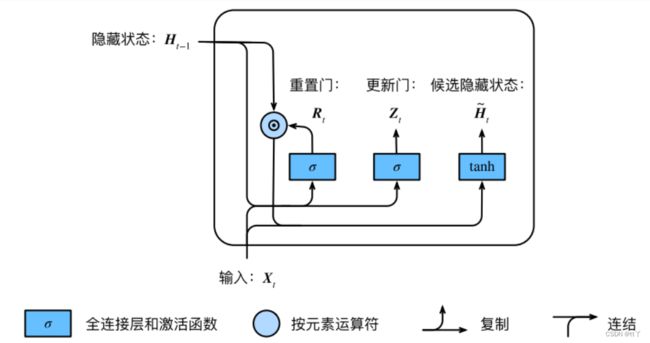
（2）候选隐藏状态

 对应计算：

以此可以看出，重置门控制了上一时间步的隐藏状态流入当前时间步的候选隐藏状态的“幅度”（如果重置门的输出接近0，则重置对应的隐藏状态元素接近0，即丢弃上一时间步的隐藏状态；如果重置门的输出接近1，则保留绝大部分上一时间步的隐藏状态）；

相对于RNN来说，他是由一个参数矩阵来控制上一时间步的隐藏状态流入当前时间步的候选隐藏状态的“幅度”，不像这边的重置门——它是由上一时间隐藏状态，当前时间输入和一些可供学习的参数共同决定；

同时，上一时间步的隐藏状态包含的可能不止是上一时刻的信息，而是可能包含所有之前的历史信息，这就可以推断出重置门可以用来丢弃和预测无关的历史信息，决定保留多少历史信息。

重置门有助于捕获序列中的短期依赖关系。

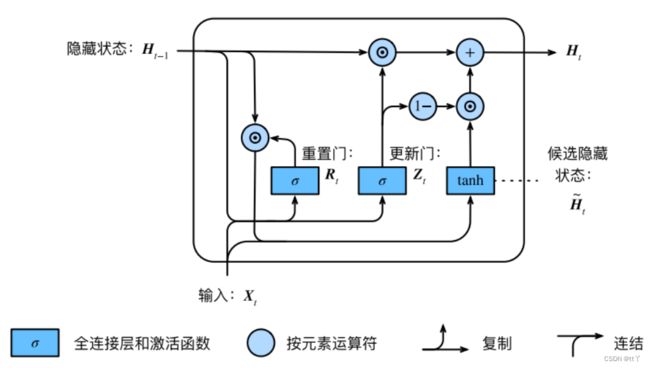
（3）隐藏状态

 对应计算：

以此可以看出更新门可以控制如何更新包含当前时间步信息的候选隐藏状态（若Z在 t' 到 t 间一直近似为1，那么在 t' 到 t 间的候选隐藏状态（含输入信息X）几乎没有流入，这也能看作是较早时刻的隐藏状态一直保留到了并传递到现在时刻（保留在中），相对于RNN与上面的分析类似。

因为它能长期保存以前的部分关键信息并进行传递，所以可以起到缓解梯度消失的问题。

 更新门有助于捕获序列中的长期依赖关系

总结：

       更新门用于控制前一时刻的状态信息被带入到当前状态中的程度，更新门的值越大说明前一时刻的状态信息带入越多；

       重置门用于控制忽略前一时刻的状态信息的程度，重置门的值越小说明忽略得越多。

（4）输出

2、反向传播

已知dY（注：*是矩阵乘法，•是矩阵上对应元素相乘）

；；

对于链式法则涉及到候选隐藏状态的，我们设为

对于链式法则涉及到更新门的，我们设为

对于链式法则涉及到重置门的，我们设为

对于候选隐藏状态中的参数：

；；

对于更新门中的参数：

；；

对于重置门中的参数：

；；

对于：

---

三、GRU的优缺点

1、优点

       GRU和LSTM作用相同，在捕捉长序列语义关联时，能有效抑制梯度消失或爆炸， 效果都优于传统RNN，但计算复杂度相比LSTM要小。

      GRU模型简单 ，参数量更少，训练速度更快，因此更适用于构建较大的网络。它只有两个门控，从计算角度看，效率更高，它的可扩展性有利于构筑较大的模型；但LSTM因为它具有三个门控，更加的强大和灵活，表达能力更强，同时训练速度会比GRU慢一些。

2、缺点

      GRU仍然不能完全解决梯度消失问题，同时其作为RNN的变体，有着RNN结构本身的一大弊端——不可并行计算，这在数据量和模型体量逐步增大的未来，是RNN发展的关键瓶颈。

---

四、代码实现GRU

这里只展示我用numpy搭建的GRU网络，并且实现对“abcdefg abcdefg abcdefg”序列数据的预测。详细地可以在我的github的GRU文件夹上看，包括用pytorch实现的GRU实现文本生成，以及这个numpy搭建的GRU实现对序列数据预测的完整版本。

http://​​​​​​https://github.com/tt-s-t/Deep-Learning.git

首先我们写一个类来实现前向传播，反向传播和最后预测。

1、numpy实现GRU模型

（1）前期准备

import numpy as np

def sigmoid(x):
    x_ravel = x.ravel()  # 将numpy数组展平
    length = len(x_ravel)
    y = []
    for index in range(length):
        if x_ravel[index] >= 0:
            y.append(1.0 / (1 + np.exp(-x_ravel[index])))
        else:
            y.append(np.exp(x_ravel[index]) / (np.exp(x_ravel[index]) + 1))
    return np.array(y).reshape(x.shape)

def tanh(x):
    result = (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
    return result

（2）初始化参数

class GRU(object):
    def __init__(self, input_size, hidden_size):
        self.input_size = input_size
        self.hidden_size = hidden_size
        #重置门
        self.Wxr = np.random.randn(input_size, hidden_size)
        self.Whr = np.random.randn(hidden_size, hidden_size)
        self.B_r  = np.zeros((1, hidden_size))
        #更新门
        self.Wxz = np.random.randn(input_size, hidden_size)
        self.Whz = np.random.randn(hidden_size, hidden_size)
        self.B_z = np.zeros((1, hidden_size))
        #候选隐藏状态
        self.Wxh = np.random.randn(input_size, hidden_size)
        self.Whh = np.random.randn(hidden_size, hidden_size)
        self.B_h = np.zeros((1, hidden_size))
        #输出
        self.W_o = np.random.randn(hidden_size, input_size)
        self.B_o = np.zeros((1, input_size))

（3）前向传播

    def forward(self,X,Ht_1): #前向传播
        #存储
        self.rt_stack = {} #重置门存储
        self.zt_stack = {} #更新门存储
        self.hht_stack = {} #候选隐藏状态存储
        self.X_stack = {} #X存储
        self.Ht_stack = {} #隐藏状态存储
        self.Y_stack = {} #输出存储

        self.Ht_stack[-1] = Ht_1
        self.T = X.shape[0]

        for t in range(self.T):
            self.X_stack[t] = X[t].reshape(-1,1).T
            #重置门
            net_r = np.matmul(self.X_stack[t], self.Wxr) + np.matmul(self.Ht_stack[t-1], self.Whr) + self.B_r
            rt = sigmoid(net_r)
            self.rt_stack[t] = rt
            #更新门
            net_z = np.matmul(self.X_stack[t], self.Wxz) + np.matmul(self.Ht_stack[t-1], self.Whz) + self.B_z
            zt = sigmoid(net_z)
            self.zt_stack[t] = zt
            #候选隐藏状态
            net_hh = np.matmul(self.X_stack[t], self.Wxh) + np.matmul(rt*self.Ht_stack[t-1], self.Whh) + self.B_h
            hht = tanh(net_hh)
            self.hht_stack[t] = hht
            #隐藏状态
            Ht = zt*self.Ht_stack[t-1] + (1-zt)*hht
            self.Ht_stack[t] = Ht
            #输出
            Ot = np.matmul(Ht, self.W_o) + self.B_o
            Yt = np.exp(Ot) / np.sum(np.exp(Ot)) #softmax
            self.Y_stack[t] = Yt

（4）后向传播

    def backward(self,target,lr):
        #初始化
        dW_o, dB_o, dH, dH_1 = np.zeros_like(self.W_o), np.zeros_like(self.B_o), np.zeros_like(self.Ht_stack[-1]), np.zeros_like(self.Ht_stack[-1])

        dWxh, dWhh, dBh = np.zeros_like(self.Wxh), np.zeros_like(self.Whh), np.zeros_like(self.B_h)
        dWxr, dWhr, dBr = np.zeros_like(self.Wxr), np.zeros_like(self.Whr), np.zeros_like(self.B_r)
        dWxz, dWhz, dBz = np.zeros_like(self.Wxz), np.zeros_like(self.Whz), np.zeros_like(self.B_z)

        self.loss = 0

        for t in reversed(range(self.T)): #反过来开始，因为像隐藏状态求偏导那样，越往前面分支越多       
            dY = self.Y_stack[t] - target[t].reshape(-1,1).T
            self.loss += -np.sum(np.log(self.Y_stack[t]) * target[t].reshape(-1,1).T)
            #对输出的参数
            dW_o += np.matmul(self.Ht_stack[t].T,dY)
            dB_o += dY

            dH = np.matmul(dY, self.W_o.T) + dH_1 #dH更新

            #对有关更新门，重置门，候选隐藏状态中参数的求导的共同点
            dnet_hht = dH * (1-self.zt_stack[t]) * (1-self.hht_stack[t] * self.hht_stack[t]) #候选隐藏状态
            dnet_Z = dH * (self.Ht_stack[t-1] - self.hht_stack[t]) * self.zt_stack[t] *(1 - self.zt_stack[t]) #更新门
            dnet_R = np.matmul(dnet_hht, self.Whh) * self.Ht_stack[t-1] * self.rt_stack[t] *(1 - self.rt_stack[t]) #重置门

            #候选隐藏状态中参数
            dWxh += np.matmul(self.X_stack[t].T, dnet_hht)
            dWhh += np.matmul((self.rt_stack[t]*self.Ht_stack[t-1]).T, dnet_hht)
            dBh += dnet_hht

            #更新门
            dWxz += np.matmul(self.X_stack[t].T, dnet_Z)
            dWhz += np.matmul(self.Ht_stack[t-1].T, dnet_Z)
            dBz += dnet_Z

            #重置门
            dWxr += np.matmul(self.X_stack[t].T, dnet_R)
            dWhr += np.matmul(self.Ht_stack[t-1].T, dnet_R)
            dBr += dnet_R

            #Ht-1
            dH_1 = dH * self.zt_stack[t] + np.matmul(dnet_hht, self.Whh) * self.rt_stack[t] + np.matmul(dnet_R, self.Whr) + np.matmul(dnet_Z, self.Whz)

        #候选隐藏状态
        self.Wxh += -lr * dWxh
        self.Whh += -lr * dWhh
        self.B_h += -lr * dBh
        #更新门
        self.Wxz += -lr * dWxz
        self.Whz += -lr * dWhz
        self.B_z += -lr * dBz
        #重置门
        self.Wxr += -lr * dWxr
        self.Whr += -lr * dWhr
        self.B_r += -lr * dBr

        return self.loss

（5）预测

    def pre(self,input_onehot,h_prev,next_len,vocab): #input_onehot为输入的一个词的onehot编码，next_len为需要生成的单词长度，vocab是"索引-词"的词典
        xs, hs = {}, {} #字典形式存储
        hs[-1] = np.copy(h_prev) #隐藏变量赋予
        xs[0] = input_onehot
        pre_vocab = []
        for t in range(next_len):
            #重置门
            net_r = np.matmul(xs[t], self.Wxr) + np.matmul(hs[t-1], self.Whr) + self.B_r
            rt = sigmoid(net_r)
            #更新门
            net_z = np.matmul(xs[t], self.Wxz) + np.matmul(hs[t-1], self.Whz) + self.B_z
            zt = sigmoid(net_z)
            #候选隐藏状态
            net_hh = np.matmul(xs[t], self.Wxh) + np.matmul(rt*hs[t-1], self.Whh) + self.B_h
            hht = tanh(net_hh)
            #隐藏状态
            hs[t] = zt*hs[t-1] + (1-zt)*hht
            #输出
            Ot = np.matmul(hs[t], self.W_o) + self.B_o
            Yt = np.exp(Ot) / np.sum(np.exp(Ot)) #softmax
            pre_vocab.append(vocab[np.argmax(Yt)])

            xs[t+1] = np.zeros((1, self.input_size)) # init
            xs[t+1][0,np.argmax(Yt)] = 1
        return pre_vocab

2、调用我们实现的GRU进行训练与预测

from gru_model import GRU
import numpy as np
import math

class Dataset(object):
    def __init__(self,txt_data, sequence_length):
        self.txt_len = len(txt_data) #文本长度
        vocab = list(set(txt_data)) #所有字符合集
        self.n_vocab = len(vocab) #字典长度
        self.sequence_length = sequence_length
        self.vocab_to_index = dict((c, i) for i, c in enumerate(vocab)) #词-索引字典
        self.index_to_vocab = dict((i, c) for i, c in enumerate(vocab)) #索引-词字典
        self.txt_index = [self.vocab_to_index[i] for i in txt_data] #输入文本的索引表示

    def one_hot(self,input):
        onehot_encoded = []
        for i in input:
            letter = [0 for _ in range(self.n_vocab)] 
            letter[i] = 1
            onehot_encoded.append(letter)
        onehot_encoded = np.array(onehot_encoded)
        return onehot_encoded
    
    def __getitem__(self, index):
        return (
            self.txt_index[index:index+self.sequence_length],
            self.txt_index[index+1:index+self.sequence_length+1]
        )

#输入的有规律的序列数据
txt_data = "abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg abcdefg"

#config
max_epoch = 5000
sequence_length = 6
dataset = Dataset(txt_data,sequence_length)
batch_num = math.ceil(dataset.txt_len /sequence_length) #向上取整
hidden_size = 16
lr = 1e-4

model = GRU(dataset.n_vocab,hidden_size)

#训练
for epoch in range(max_epoch):
    h_prev = np.zeros((1, hidden_size))
    loss = 0
    for b in range(batch_num):
        (x,y) = dataset[b]
        input = dataset.one_hot(x)
        target = dataset.one_hot(y)
        ps = model.forward(input,h_prev) #注意：每个batch的h都是从0初始化开始，batch与batch间的隐藏状态没有关系
        loss += model.backward(target,lr)
    print("epoch: ",epoch)
    print("loss: ",loss/batch_num)

#预测
input_txt = 'a'
input_onehot = dataset.one_hot([dataset.vocab_to_index[input_txt]])
next_len = 50 #预测后几个word
h_prev = np.zeros((1, hidden_size))
pre_vocab = ['a']
pre_vocab1 = model.pre(input_onehot,h_prev,next_len,dataset.index_to_vocab)
pre_vocab = pre_vocab + pre_vocab1
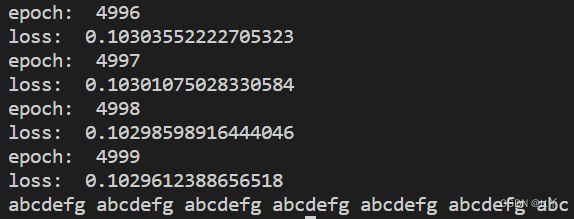
print(''.join(pre_vocab))

3、result

---

 欢迎大家在评论区批评指正，谢谢大家~