论文解读(NWR)《Graph Auto-Encoder via Neighborhood Wasserstein Reconstruction》
优质资源分享
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| Python实战微信订餐小程序 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| Python量化交易实战 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
论文信息
论文标题:Graph Auto-Encoder via Neighborhood Wasserstein Reconstruction论文作者:Shaked Brody, Uri Alon, Eran Yahav论文来源:2022,ICLR论文地址:download 论文代码:download
1 Abstract
图神经网络(GNNs)近年来引起了广泛的研究关注,主要是在半监督学习的背景下。当任务不可知的表示是首选或监督完全不可用时,自动编码器框架与无监督GNN训练的自然图重建目标一起使用。然而,现有的图自动编码器是通过设计来重建直接链路的,因此以这种方式训练的gnn只针对面向邻近的图挖掘任务进行优化,当拓扑结构很重要时就会失败。在本研究中,我们重新讨论了gnn的图编码过程,它本质上学习了将每个节点的邻域信息编码为一个嵌入向量,并提出了一种新的图解码器,通过邻域瓦瑟斯坦重建(NWR)来重建关于邻近性和结构的整个邻域信息。
具体来说,NWR从每个节点的GNN嵌入中,联合预测其节点度和邻居特征分布,其中分布预测采用了基于瓦瑟斯坦距离的最优传输损失。在合成网络数据集和真实网络数据集上的大量实验表明,使用NWR学习的无监督节点表示在面向结构的图挖掘任务中具有更大的优势,同时在面向接近的图挖掘任务中也具有竞争性能。
2 Introduction
现有的图自动编码:
-
- 例如 GAE(Kipf & Welling, 2016)学习的节点表示由于其优化简单的重建目标以至无法区分像 (2, 4) 和 (3, 5)这样的点;
- 例如 GraphWave (Donnat et al., 2018) 这样的面向结构的嵌入模型不考虑节点特征和空间接近度,无法区分像 (0, 1), (2, 4) 和 (3,5) 这样的节点对;
- 例如 GAE(Kipf & Welling, 2016)学习的节点表示由于其优化简单的重建目标以至无法区分像 (2, 4) 和 (3, 5)这样的点;
具体地说,本文将解码过程描述为从通过 GNN 编码器获得的多跳邻居表示上定义的一系列概率分布中进行迭代采样。然后,将重构损失分解为三个部分,即采样数(节点度)、邻居表示分布和节点特征。本文最重要的术语是“ 邻居表示分布重建”(neighborrepresentation distribution reconstruction),本文采用了基于 Wasserstein distance 的最优传输损失,因此将这个新的框架命名为 Neighborhood Wasserstein Reconstruction Graph Auto-Encoder (NWR-GAE).。如 Figure1 所示,NWR-GAE可以有效地在不同的角度区分所有不同的节点对,并简明地反映出它们在低维嵌入空间中的相似性。
为了更好地理解这一点,我们仔细分析了通过GNN在每个节点表示中编码的信息源。假设采用一个标准的消息传递 GNN (Gilmer等人,2017) 作为编码器,这是一个通用框架,包括 GCN 、GraphSAGE、GAT、GIN 等等。在 k-hop 消息传递后,在节点 vvv 的表示中编码的信息来源本质上来自于 vvv 的 k−hopk−hopk-hop 邻域(Fig.2)。因此,节点 vvv 的良好表示应该捕获其 kkk 跳邻域中所有节点的特征信息,这与下游任务是无关的。请注意,这可能不是理想的,因为 k−hopk−hopk-hop 邻域外的节点也可能提供有用的信息,但由于 GNN 编码器的架构,这是基于 GNN 的图自动编码器可以期望做的。这一观察结果促使我们研究了一种新的图解码器,该解码器可以更好地促进基于 GNN 的图自动编码器的目标。我们将在 Sec3 中正式确立这一原则。
Relation to the InfoMax principle
最近,DGI、EGI 在无监督GNN训练方法中使用了对比学习,并可能捕获定向链接之外的信息。它们采用了互信息最大化规则 (InfoMax),它本质上是为了最大化学习到的表示和原始数据之间的某些对应关系。例如,DGI 最大化了节点表示与节点所属的图之间的对应关系,但这并不能保证重建节点邻域的结构信息。最近的研究甚至表明,最大化这种对应关系可能只捕获与下行任务无关的噪声信息,因为噪声信息本身足以让模型实现 InfoMax,我们的实验再次证明了这一点。相反,我们的目标是让节点表示不仅捕获信息来区分节点,而且捕获尽可能多的信息来重建邻域的特征和结构。
Optimal-transport (OT) losses
许多机器学习问题依赖于两个概率测度量之间的距离的描述。当两个分布有非重叠的部分时,fff 散度存在非连续的问题。
Suppose we have two probability distributions, PPP and QQQ :
∀(x,y)∈P,x=0 and y∼U(0,1)∀(x,y)∈Q,x=θ,0≤θ≤1 and y∼U(0,1)∀(x,y)∈P,x=0 and y∼U(0,1)∀(x,y)∈Q,x=θ,0≤θ≤1 and y∼U(0,1)\forall(x, y) \in P, x=0 \text { and } y \sim U(0,1) \forall(x, y) \in Q, x=\theta, 0 \leq \theta \leq 1 \text { and } y \sim U(0,1)
When θ≠0θ≠0\theta \neq 0 :
DKL(P∥Q)=∑x=0,y∼U(0,1)1⋅log10=+∞DKL(P‖Q)=∑x=0,y∼U(0,1)1⋅log10=+∞D_{K L}(P | Q) =\sum\limits _{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty DKL(Q∥P)=∑x=0,y∼U(0,1)1⋅log10=+∞DKL(Q‖P)=∑x=0,y∼U(0,1)1⋅log10=+∞D_{K L}(Q | P) =\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{0}=+\infty DJS(P,Q)=12(∑x=0,y∼U(0,1)1⋅log11/2+∑x=0,y∼U(0,1)1⋅log11/2)=log2DJS(P,Q)=12(∑x=0,y∼U(0,1)1⋅log11/2+∑x=0,y∼U(0,1)1⋅log11/2)=log2D_{J S}(P, Q) =\frac{1}{2}\left(\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}+\sum\limits_{x=0, y \sim U(0,1)} 1 \cdot \log \frac{1}{1 / 2}\right)=\log 2 W(P,Q)=|θ|W(P,Q)=|θ|W(P, Q) =|\theta|
But when θ=0θ=0\theta = 0, two distributions are fully overlapped:
DKL(P∥Q)=DKL(Q∥P)=DJS(P,Q)=0DKL(P‖Q)=DKL(Q‖P)=DJS(P,Q)=0D_{K L}(P | Q) =D_{K L}(Q | P)=D_{J S}(P, Q)=0
W(P,Q)=0=|θ|W(P,Q)=0=|θ|W(P, Q) =0=|\theta|
因此,OT 损失经常被采用,并在生成模型和领域适应中取得了巨大的成功。OT 损失已被用于构建非图形数据的变分自动编码器。但应该注意的是,我们的工作并不是这些工作的面向图数据的泛化:他们使用 OT 损失来描述变分分布和数据经验分布之间的距离,而我们的模型甚至不使用变分分布。我们的模型可以进一步改进为一个变分自编码器,但我们把它作为一个未来的方向。
在这里,我们给出了一个基于 2-Wasserstein distance 的常用的 OT 损失,这将在稍后使用。
Definition 2.1. Let PP\mathcal{P}, QQ\mathcal{Q} denote two probability distributions with finite second moment defined on Z⊆RmZ⊆Rm\mathcal{Z} \subseteq \mathbb{R}^{m} . The 2-Wasserstein distance between PP\mathcal{P} and QQ\mathcal{Q} defined on ZZ\mathcal{Z}, Z′⊆RmZ′⊆Rm\mathcal{Z}^{\prime} \subseteq \mathbb{R}^{m} is the solution to the optimal mass transportation problem with ℓ2ℓ2\ell_{2} transport cost (Villani, 2008):
W2(P,Q)=(infγ∈Γ(P,Q)∫Z×Z′∥Z−Z′∥22dγ(Z,Z′))1/2W2(P,Q)=(infγ∈Γ(P,Q)∫Z×Z′‖Z−Z′‖22dγ(Z,Z′))1/2\mathcal{W}_{2}(\mathcal{P}, \mathcal{Q})=\left(\inf _{\gamma \in \Gamma(\mathcal{P}, \mathcal{Q})} \int_{\mathcal{Z} \times \mathcal{Z}{\prime}}\left|Z-Z{\prime}\right|_{2}^{2} d \gamma\left(Z, Z{\prime}\right)\right){1 / 2}
where Γ(P,Q)Γ(P,Q)\Gamma(\mathcal{P}, \mathcal{Q}) contains all joint distributions of (Z,Z′)(Z,Z′)\left(Z, Z^{\prime}\right) with marginals PP\mathcal{P} and QQ\mathcal{Q} respectively.
3 Methods
预先定义 :
-
- Encoder:ϕϕ\phi
- Decoder:ψψ\psi
- Encoder:ϕϕ\phi
Encoder 可以是任何基于消息传递的 GNNs,Decoder 可以分成三部分:ψ=(ψs,ψp,ψd)ψ=(ψs,ψp,ψd)\psi=\left(\psi_{s}, \psi_{p}, \psi_{d}\right)
3.1 Neighborhood peconstruction principle
为了简化阐述,我们从 1 跳邻域重建开始。我们基于 XXX 用 H(0)H(0)H^{(0)} 初始化节点表示。对于每个节点 v∈Vv∈Vv \in V,在被一个GNN层编码后,其节点表示h h(1)vhv(1)h_{v}^{(1)} 从 h(0)vhv(0)h_{v}^{(0)} 及其邻居的表示 H(0)Nv={h(0)u∣u∈Nv}HNv(0)={hu(0)∣u∈Nv}H_{\mathcal{N}_{v}}{(0)}=\left{h_{u}{(0)} \mid u \in \mathcal{N}_{v}\right} 中收集信息。因此,我们考虑以下原则,即重构来自 h(0)vhv(0)h_{v}^{(0)} 和 H(0)NvHNv(0)H_{\mathcal{N}_{v}}^{(0)} 的信息。因此,我们有了
minϕ,ψ s.t. ∑v∈VM((h(0)v,H(0)Nv),ψ(h(1)v))h(1)v=ϕ(h(0)v,H(0)Nv),∀v∈V(2)minϕ,ψ∑v∈VM((hv(0),HNv(0)),ψ(hv(1))) s.t. hv(1)=ϕ(hv(0),HNv(0)),∀v∈V(2)\begin{array} {l}\underset{\phi, \psi}{\text{min}} & \sum\limits _{v \in V} \mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}^{(1)}\right)\right)\\text { s.t. } & h_{v}{(1)}=\phi\left(h_{v}{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \forall v \in V\end{array} \quad\quad\quad(2)
式中,M(⋅,⋅)M(⋅,⋅)\mathcal{M}(\cdot, \cdot) 定义了重建损失。MMM 可以分为两部分,分别测量自特征重建和邻域重建:
M((h(0)v,H(0)Nv),ψ(h(1)v))=Ms(h(0)v,ψ(h(1)v))+Mn(H(0)Nv,ψ(h(1)v))(3)M((hv(0),HNv(0)),ψ(hv(1)))=Ms(hv(0),ψ(hv(1)))+Mn(HNv(0),ψ(hv(1)))(3)\mathcal{M}\left(\left(h_{v}^{(0)}, H_{\mathcal{N}_{v}}^{(0)}\right), \psi\left(h_{v}{(1)}\right)\right)=\mathcal{M}_{s}\left(h_{v}{(0)}, \psi\left(h_{v}{(1)}\right)\right)+\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}{(0)}, \psi\left(h_{v}^{(1)}\right)\right)\quad\quad\quad(3)
请注意,MsMs\mathcal{M}_{s} 的工作原理就像一个基于标准的前馈神经网络(FNN)的自动编码器的重建损失一样,所以我们采用了
Ms(h(0)v,ψ(h(1)v))=∥∥h(0)v−ψs(h(1)v)∥∥2(4)Ms(hv(0),ψ(hv(1)))=‖hv(0)−ψs(hv(1))‖2(4)\mathcal{M}_{s}\left(h_{v}^{(0)}, \psi\left(h_{v}{(1)}\right)\right)=\left|h_{v}{(0)}-\psi_{s}\left(h_{v}{(1)}\right)\right|{2}\quad\quad\quad(4)
MnMn\mathcal{M}_{n} 很难被描述,因为它测量的是重建一组特征 H(0)NvHNv(0)H_{\mathcal{N}_{v}}^{(0)} 的损失。有两个基本的挑战:首先,在现实网络中,节点度的分布通常是长尾的,节点邻居的集合可能有非常不同的大小。其次,为了比较甚至两个大小相等的集合,也必须解决一个匹配问题,因为可以假定集合中没有固定的元素顺序。如果集合的大小较大,则解决匹配问题的复杂性很高。我们通过将邻域信息解耦为概率分布和采样数来解决上述挑战。具体来说,对于节点 vvv,邻域信息被表示为 i.i.d .的经验实现从 P(0)vPv(0)\mathcal{P}_{v}^{(0)} 中采样 dvdvd_{v} 元素,其中 P(0)v≜1dv∑u∈Nvδh(0)uPv(0)≜1dv∑u∈Nvδhu(0)\mathcal{P}_{v}^{(0)} \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(0)}}。基于这一观点,我们可以将重建分别分解为节点度和分布的部分,其中不同大小的节点邻域得到了正确的处理。具体来说,我们采用
Mn(H(0)Nv,ψ(h(1)v))=(dv−ψd(h(1)v))2+W22(P(0)v,ψ(1)p(h(1)v))(5)Mn(HNv(0),ψ(hv(1)))=(dv−ψd(hv(1)))2+W22(Pv(0),ψp(1)(hv(1)))(5)\mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(0)}, \psi\left(h_{v}{(1)}\right)\right)=\left(d_{v}-\psi_{d}\left(h_{v}{(1)}\right)\right){2}+\mathcal{W}_{2}{2}\left(\mathcal{P}_{v}^{(0)}, \psi_{p}{(1)}\left(h_{v}{(1)}\right)\right)\quad\quad\quad(5)
Generalizing to k-hop neighborhood reconstruction
根据上述对第一个情况的推导,我们可以类似地推广基于 h(i)vhv(i)h_{v}^{(i)} 的重构 (h(i−1)v,H(i−1)Nv)(hv(i−1),HNv(i−1))\left(h_{v}^{(i-1)}, H_{\mathcal{N}_{v}}^{(i-1)}\right) 的损失。然后,如果我们将所有节点 v∈Vv∈Vv \in V 和所有跳 1≤i≤k1≤i≤k1 \leq i \leq k 的损失相加,我们可以实现 kkk 跳邻域重建的目标。我们可以进一步简化这一目标。通常,只有最终的层表示 H(k)H(k)H^{(k)} 被用作输出降维表示。过多的中间跳使模型难以训练,收敛速度慢。因此,我们采用了一种更经济的方式,合并了多步重建:
也就是说,我们期望 h(k)vhv(k)h_{v}^{(k)} 直接重构 H(i)NvHNv(i)H_{\mathcal{N}_{v}}^{(i)},即使 i M′((h(0)v,{H(i)Nv∣0≤i≤k−1}),ψ(h(k)v))=Ms(h(0)v,ψ(h(k)v))+∑i=0k−1Mn(H(i)Nv,ψ(h(k)v))=λs∥∥h(0)v−ψs(h(k)v)∥∥2+λd(dv−ψd(h(k)v))2+∑i=0k−1W22(P(i)v,ψ(i)p(h(k)v))(6)M′((hv(0),{HNv(i)∣0≤i≤k−1}),ψ(hv(k)))=Ms(hv(0),ψ(hv(k)))+∑i=0k−1Mn(HNv(i),ψ(hv(k)))=λs‖hv(0)−ψs(hv(k))‖2+λd(dv−ψd(hv(k)))2+∑i=0k−1W22(Pv(i),ψp(i)(hv(k)))(6)\begin{array}{l}&\mathcal{M}{\prime}\left(\left(h_{v}{(0)},\left{H_{\mathcal{N}_{v}}^{(i)} \mid 0 \leq i \leq k-1\right}\right), \psi\left(h_{v}{(k)}\right)\right)=\mathcal{M}_{s}\left(h_{v}{(0)}, \psi\left(h_{v}{(k)}\right)\right)+\sum\limits_{i=0}{k-1} \mathcal{M}_{n}\left(H_{\mathcal{N}_{v}}^{(i)}, \psi\left(h_{v}^{(k)}\right)\right) \&=\lambda_{s}\left|h_{v}{(0)}-\psi_{s}\left(h_{v}{(k)}\right)\right|{2}+\lambda_{d}\left(d_{v}-\psi_{d}\left(h_{v}{(k)}\right)\right){2}+\sum\limits_{i=0}{k-1} \mathcal{W}_{2}{2}\left(\mathcal{P}_{v}{(i)}, \psi_{p}{(i)}\left(h_{v}{(k)}\right)\right)\end{array}\quad(6) 其中 ψsψs\psi_{s} 是解码初始特征,ψdψd\psi_{d} 是度解码,ψ(i)pψp(i)\psi_{p}^{(i)},0≤i≤k−10≤i≤k−10 \leq i \leq k-1 是解码 iii 层邻域表示分布 P(i)v(:≜1dv∑u∈Nvδh(i)u)Pv(i)(:≜1dv∑u∈Nvδhu(i))\mathcal{P}_{v}^{(i)}\left(: \triangleq \frac{1}{d_{v}} \sum\limits _{u \in \mathcal{N}_{v}} \delta_{h_{u}^{(i)}}\right)。λsλs\lambda_{s} 和 λdλd\lambda_{d} 为非负性超参数。因此,kkk 跳邻域重建的全部目标是 minϕ,ψ∑v∈VM′((h(0)v,{H(i−1)Nv∣1≤i≤k}),ψ(h(k)v)) s.t. H(i)=ϕ(i)(H(i−1)),1≤i≤kminϕ,ψ∑v∈VM′((hv(0),{HNv(i−1)∣1≤i≤k}),ψ(hv(k))) s.t. H(i)=ϕ(i)(H(i−1)),1≤i≤k\begin{array}{l} \underset{\phi, \psi}{\text{min}}\quad \sum\limits _{v \in V} \mathcal{M}{\prime}\left(\left(h_{v}{(0)},\left{H_{\mathcal{N}_{v}}^{(i-1)} \mid 1 \leq i \leq k\right}\right), \psi\left(h_{v}^{(k)}\right)\right)\ \text { s.t. }\quad H{(i)}=\phi{(i)}\left(H^{(i-1)}\right), \quad1 \leq i \leq k\end{array} 其中,ϕ={ϕ(i)∣1≤i≤k}ϕ={ϕ(i)∣1≤i≤k}\phi=\left{\phi^{(i)} \mid 1 \leq i \leq k\right} 包括 kkk 个GNN层,M′M′\mathcal{M}^{\prime} 在 Eq.6Eq.6\text{Eq.6} 中定义。 Remark 3.1 我们的 NRP 本质上是将节点邻域 H(i)NvHNv(i)H_{\mathcal{N}_{v}}^{(i)} 表示为一个采样数(节点度 dvdvd_v )加上一个邻居表示 P(i)vPv(i)\mathcal{P}_{v}^{(i)} 的分布(Eq.5.6Eq.5.6\text{Eq.5.6})。我们采用 Wasserstein distance 来表征分布重构损失,因为 P(i)vPv(i)\mathcal{P}_{v}^{(i)} 在连续空间中具有原子非零测度支持,在连续空间中不能应用 fff 散度族的分布重构损失。可以应用最大平均差异,但它需要指定一个核函数。 ψ(i)p(h(k)v)=FNN(i)p(ξ),ξ∼N(μv,Σv) where μv=FNNμ(h(k)v),Σv=diag(exp(FNNσ(h(k)v)))ψp(i)(hv(k))=FNNp(i)(ξ),ξ∼N(μv,Σv) where μv=FNNμ(hv(k)),Σv=diag(exp(FNNσ(hv(k))))\begin{array}{l}\psi_{p}{(i)}\left(h_{v}{(k)}\right)=\operatorname{FNN}_{p}^{(i)}(\xi),\quad \xi \sim \mathcal{N}\left(\mu_{v}, \Sigma_{v}\right)\\text { where }\quad \mu_{v}=\operatorname{FNN}_{\mu}\left(h_{v}^{(k)}\right), \quad\Sigma_{v}=\operatorname{diag}\left(\exp \left(\operatorname{FNN}_{\sigma}\left(h_{v}^{(k)}\right)\right)\right)\end{array} Theorem 3.1. For any ϵ>0ϵ>0\epsilon>0 , if the support of the distribution P(i)vPv(i)\mathcal{P}_{v}^{(i)} lies in a bounded space of RmRm\mathbb{R}^{m} , there exists a FNNu(⋅):Rm→RFNNu(⋅):Rm→RFNN u(\cdot): \mathbb{R}^{m} \rightarrow \mathbb{R} (and thus its gradient ∇u(⋅):Rm→Rm∇u(⋅):Rm→Rm\nabla u(\cdot): \mathbb{R}^{m} \rightarrow \mathbb{R}^{m} ) with large enough width and depth (depending on ϵϵ\epsilon ) such that W22(P(i)v,∇u(G))<ϵW22(Pv(i),∇u(G))<ϵ\mathcal{W}_{2}{2}\left(\mathcal{P}_{v}{(i)}, \nabla u(\mathcal{G})\right)<\epsilon where ∇u(G)∇u(G)\nabla u(\mathcal{G}) is the distribution generated via the mapping ∇u(ξ)∇u(ξ)\nabla u(\xi), ξ∼aξ∼a\xi \sim a mmm-dim non-degenerate Gaussian distribution. 另一个挑战是,P(i)vPv(i)\mathcal{P}_{v}^{(i)} 和 ψ(i)p(h(k)v)ψp(i)(hv(k))\psi_{p}{(i)}\left(h_{v}{(k)}\right) 之间的 Wasserstein distance 没有一个封闭的形式。因此,我们采用 empirical Wasserstein distance。对于每一次正向传递,模型将得到 qqq 个采样节点 NvNv\mathcal{N}_{v},记为 v1,v2,…,vqv1,v2,…,vqv_{1}, v_{2}, \ldots, v_{q} 因此,{h(i)vj∣1≤j≤q}{hvj(i)∣1≤j≤q}\left{h_{v_{j}}^{(i)} \mid 1 \leq j \leq q\right} 是来自 P(i)vPv(i)\mathcal{P}_{v}^{(i)} 的 qqq 个样本;接下来,从 N(μv,Σv)N(μv,Σv)\mathcal{N}\left(\mu_{v}, \Sigma_{v}\right) 采样的 qqq 个样本定义为 ξ1,ξ2,…,ξqξ1,ξ2,…,ξq\xi_{1}, \xi_{2}, \ldots, \xi_{q},因此 {h(i,j)v=FNN(i)p(ξj)∣1≤j≤q}{hv(i,j)=FNNp(i)(ξj)∣1≤j≤q}\left{\hat{h}_{v}^{(i, j)}=\operatorname{FNN}_{p}^{(i)}\left(\xi_{j}\right) \mid 1 \leq j \leq q\right} 是从 ψ(i)p(h(k)v)ψp(i)(hv(k))\psi_{p}{(i)}\left(h_{v}{(k)}\right) 中采样的 qqq 个样本;在 Eq.6Eq.6\text{Eq.6} 采用以下经验抵消损失 ∑i=0k−1W22(P(i)v,ψ(i)p(h(k)v))∑i=0k−1W22(Pv(i),ψp(i)(hv(k)))\sum\limits _{i=0}^{k-1} \mathcal{W}_{2}{2}\left(\mathcal{P}_{v}{(i)}, \psi_{p}{(i)}\left(h_{v}{(k)}\right)\right) 上述损失的计算是基于求解一个匹配问题,需要具有 O(q3)O(q3)O(q^3) 复杂度的匈牙利算法。可以采用更有效的替代损失类型,如基于贪婪近似的倒角损失(Fanetal.,2017)或基于连续松弛的辛角损失(Cuturi,2013),其复杂性为 O(q2)O(q2)O(q^2)。在我们的实验中,由于 qqq 是固定为一个小常数,比如5,我们使用等式8基于匈牙利匹配,不引入太多的计算开销。虽然没有直接相关,但我们想强调一些最近的工作,即使用 OT 损失作为两个图之间的距离,其中采用了这两个图的两组节点嵌入之间的瓦瑟斯坦距离(Xuetal.,2019a;b)。借用这样一个概念,我们可以查看我们的 OT 损失也来测量原始图和解码图之间的距离。 重构初始特征 h(0)vhv(0)h_{v}^{(0)} 的解码器 ψsψs\psi_{s} 是一个 FNN。重构节点度的解码器 ψdψd\psi_{d} 是一个 FNN+指数神经元,使其值非负。 ψs(h(k)v)ψd(h(k)v)==FNNs(h(k)v)exp(FNNd(h(k)v))(9)ψs(hv(k))=FNNs(hv(k))ψd(hv(k))=exp(FNNd(hv(k)))(9)\begin{array}{l}\psi_{s}\left(h_{v}{(k)}\right)&=&\mathrm{FNN}_{s}\left(h_{v}{(k)}\right)\\psi_{d}\left(h_{v}^{(k)}\right)&=&\exp \left(\mathrm{FNN}_{d}\left(h_{v}^{(k)}\right)\right)\end{array}\quad\quad\quad(9) 在实际应用中,原始的节点特征 XXX 可以是非常高维的,直接重构它们可能会在节点表示中引入大量的噪声。相反,我们可以首先将 XXX 映射到一个潜在的空间来初始化 H0H0H^{0}。然而,如果 H0H0H^{0} 同时用于表示学习和重建,它就有崩溃到平凡点的风险。因此,我们通过对范数对 H0H0H^{0} 进行适当的归一化,以避免以下陷阱 {h(0)v∣v∈V}= pair-norm ({xvW∣v∈V})where W is a learnable parameter matrix. (10){hv(0)∣v∈V}= pair-norm ({xvW∣v∈V})where W is a learnable parameter matrix. (10)\begin{array}{l}\left{h_{v}^{(0)} \mid v \in V\right}=\text { pair-norm }\left(\left{x_{v} W \mid v \in V\right}\right) \ \text {where } W \text { is a learnable parameter matrix. }\end{array}\quad\quad\quad(10) 我们设计实验来评估 NWR-GAE,重点关注以下研究问题:RQ1:与最先进的无监督图嵌入基线相比,NWR-GAE在基于结构角色的合成数据集上表现如何?RQ2:NWR-GAE及其消融如何与不同类型的真实世界图形数据集上的基线进行比较?RQ3:嵌入尺寸 ddd 和采样尺寸 qqq 等主要模型参数对NWR-GAE的影响是什么? Synthetic datasets Real-world graph Datasets 1) Random walk based (DeepWalk, node2vec) 2) Structural role based (RoleX, struc2vec, GraphWave) 3) Graph auto-encoder based (GAE, VGAE, ARGVA) 4) Contrastive learning based (DGI, GraphCL, MVGRL) 在这项工作中,我们解决了现有的无监督图表示方法的局限性,并提出了第一个能够正确地捕获图中节点的接近性、结构和特征信息的模型,并在低维嵌入空间中对其进行区分编码的模型。该模型在合成和真实基准数据集上进行了广泛的测试,结果有力地支持了其声称的优势。由于它是通用的,有效的,而且在概念上也很容易理解,我们相信它有潜力作为无监督图表示学习的实际方法。在未来,它将有望看到其在不同领域的应用研究,以及仔细分析其鲁棒性和隐私性等潜在问题。 论文信息 1 Abstract 2 Introduction 3 Methods 3.1 Neighborhood peconstruction principle 3.2 Decoding distributions——Decoders \psi_{p}^{(i)}, 0 \leq i \leq k-1\psi_{p}^{(i)}, 0 \leq i \leq k-1 3.3 Further discussion-Decoders \psi_{s}\psi_{s} and \psi_{d}\psi_{d} 4 Experiments 4.1 Experimental setup 4.1.1 Datasets 4.1.2 Baselines 4.1.3 Evaluation metrics 4.2 Performance on synthetic datasets(RQ1) 4.3 Performance on real-world datasets(RQ2) 4.4 In-depth analysis of NWR-GAE 5 Conclusion __EOF__ [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F6kf0ELi-1660970375383)(https://blog.csdn.net/BlairGrowing)]Blair - 本文链接: https://blog.csdn.net/BlairGrowing/p/16599030.html
在 Eq.6Eq.6\text{Eq.6} 中的损失并不直接推动 kkk 层表示 h(k)vhv(k)h_{v}^{(k)} 来重建所有直接邻居节点的特征,但它们位于 vvv 的 kkk 跳邻域。但是,根据定义,在这个 kkk 跳邻域中存在一条长度不大于 kkk 的最短路径。因为沿路径的每两个相邻节点将引入至少一项等式之和的重建损失。这就保证了在 Eq.7Eq.7\text{Eq.7} 中的优化推动 h(k)vhv(k)h_{v}^{(k)} 来重建 vvv 的整个 k−hopk−hopk-hop 邻域。3.2 Decoding distributions——Decoders ψ(i)p,0≤i≤k−1ψp(i),0≤i≤k−1\psi_{p}^{(i)}, 0 \leq i \leq k-1
3.3 Further discussion-Decoders ψsψs\psi_{s} and ψdψd\psi_{d}
4 Experiments
4.1 Experimental setup
4.1.1 Datasets
4.1.2 Baselines
4.1.3 Evaluation metrics
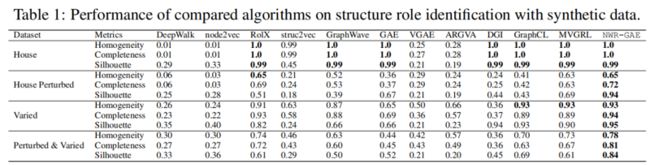
4.2 Performance on synthetic datasets(RQ1)
4.3 Performance on real-world datasets(RQ2)
4.4 In-depth analysis of NWR-GAE
5 Conclusion