特征衍生与特征筛选
Part 3.特征衍生与特征筛选
本阶开始我们将重点讨论特征工程中的特征衍生与特征筛选方法，并借此进一步提升模型效果。首先需要将此前的操作中涉及到的第三方库进行统一的导入：
# 基础数据科学运算库
import numpy as np
import pandas as pd
# 可视化库
import seaborn as sns
import matplotlib.pyplot as plt
# 时间模块
import time
# sklearn库
# 数据预处理
from sklearn import preprocessing
from sklearn.compose import ColumnTransformer
# 实用函数
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score, roc_auc_score
from sklearn.model_selection import train_test_split
# 常用评估器
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
# 网格搜索
from sklearn.model_selection import GridSearchCV
# 自定义评估器支持模块
from sklearn.base import BaseEstimator, TransformerMixin
# 自定义模块
from telcoFunc import *
# re模块相关
import inspect, re
其中telcoFunc是自定义的模块，其内保存了此前自定义的函数和类，后续新增的函数和类也将逐步写入其中，telcoFunc.py文件随课件提供，需要将其放置于当前ipy文件同一文件夹内才能正常导入。
接下来导入数据并执行Part 1中的数据清洗步骤。
# 读取数据
tcc = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
# 标注连续/离散字段
# 离散字段
category_cols = ['gender', 'SeniorCitizen', 'Partner', 'Dependents',
'PhoneService', 'MultipleLines', 'InternetService', 'OnlineSecurity', 'OnlineBackup',
'DeviceProtection', 'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 'PaperlessBilling',
'PaymentMethod']
# 连续字段
numeric_cols = ['tenure', 'MonthlyCharges', 'TotalCharges']
# 标签
target = 'Churn'
# ID列
ID_col = 'customerID'
# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 2 == tcc.shape[1]
# 连续字段转化
tcc['TotalCharges']= tcc['TotalCharges'].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
tcc['MonthlyCharges'] = tcc['MonthlyCharges'].astype(float)
# 缺失值填补
tcc['TotalCharges'] = tcc['TotalCharges'].fillna(0)
# 标签值手动转化
tcc['Churn'].replace(to_replace='Yes', value=1, inplace=True)
tcc['Churn'].replace(to_replace='No', value=0, inplace=True)
features = tcc.drop(columns=[ID_col, target]).copy()
labels = tcc['Churn'].copy()
接下来即可直接带入数据进行特征衍生。
- 特征衍生基本概念与分类
所谓特征衍生，指的是通过既有数据进行新特征的创建，特征衍生有时也被称为特征创建、特征提取等。总体来看，特征衍生有两类方法，其一是依据数据集特征进行新特征的创建，此时的特征衍生其实是一类无监督的特征衍生，例如把月度费用（‘MonthlyCharges’）和总费用（‘TotalCharges’）两列相加，创建新的一列；而另外一种情况是将数据集标签情况也纳入进行考虑来创建新的特征，此时特征衍生其实是有监督的特征衍生，如上一小节中介绍的通过决策树的建模结果对连续变量进行分箱（分箱后的列也是创建的新的一列，只是有时我们会将其替换原始列）。在大多数时候特征衍生特指无监督特征衍生，而有监督的特征衍生我们会称其为目标编码。
而无论是特征衍生还是目标编码，实现的途径都可以分为两种，其一是通过深入的数据背景和业务背景分析，进行人工字段合成，这种方法创建的字段往往具有较强的业务背景与可解释性，同时也会更加精准、有效的提升模型效果，但缺点是效率较慢，需要人工进行分析和筛选，其二则是抛开业务背景，直接通过一些简单暴力的工程化手段批量创建特征，然后从海量特征池中挑选有用的特征带入进行建模，这种方法简单高效，但工程化方法同质化严重，在竞赛时虽是必备手段，但却难以和其他同样采用工程化手段批量创建特征的竞争者拉开差距。因此，在实际应用时，往往是先通过工程化方法批量创建特征提升模型效果，然后再围绕当前建模需求具体问题具体分析，尝试人工创建一些字段来进一步提升模型效果。
当然，由于我们此前已经进行了一定程度的业务背景分析和数据探索，外加考虑到代码实现难度由易到难的讲解顺序，我们将先讨论关于人工字段合成的方法，然后再介绍工程化批量创建字段的方法。
Part 3.2 批量自动化特征衍生
在介绍完手动特征衍生方法后，接下来我们来讨论如何通过一些自动化的方法、批量创建海量特征。在正式讨论这部分内容之前，我们需要回顾和总结此前手动特征衍生过程中的部分要点，通过对这些内容的回顾，我们能快速构建对批量特征衍生方法的整体认知：
- 特征衍生的本质
所谓特征衍生，其本质指的是对既有数据信息的重新排布。需要知道的是，特征衍生本生并不是去创造更多的信息，而仅仅是借助现有的数据去组合出一些新的数据，其本质属于信息重排。当然，尽管只是信息重排，但对于建模结果的提升效果却是显而易见的。
- 特征衍生的过程
通过上面手动特征衍生的过程，不难发现，特征衍生的“信息重排”的过程就是简单的围绕单个列进行变换或者围绕多个列进行组合。例如，new_customer字段的创建，其本质上就是围绕tenure字段进行的变换，即把所有tenure取值为1的用户都标记为1，其他用户标记为0，当然，如果我们更进一步来进行思考，这其实就是tenure字段进行独热编码后的某一列；再比如，service_num字段其本质就是所有记录各项服务购买情况的字段（先转化为数值型变量再）进行求和汇总的结果，即多列进行组合变换。
- 手动特征衍生与批量特征衍生
当然，无论是从特征衍生的本质、还是从特征衍生的过程上来看，接下来将要介绍的批量自动化特征衍生，并没有超出上述介绍的范畴，即批量特征衍生同样也是数据信息的重排过程，并且执行过程上，同样也是借助单独的列进行变换或者是多个列进行组合变换。只不过不同的是，批量特征衍生并不会像手动特征衍生一样，先从思路出发、再分析数据集当前的业务背景或数据分布规律、最后再进行特征衍生，而是优先考虑从方法出发，直接考虑单个列、不同的列之间有哪些可以衍生出新特征的方法，然后尽可能去衍生出更多的特征。
例如，我们只需要对tenure字段进行独热编码就可以一次性衍生出73个列，甚至，我们还可以随机选取tenure字段的两个不同值（例如tenure=15、17），并把这两个时间点入网的用户标记为1、其他用户标记为0，而在随机选取的情况下，这里就有 C 73 2 = 73 ∗ 72 2 = 2628 C^2_{73}=\frac{73*72}{2}=2628 C732=273∗72=2628种特征衍生的方法。
- 特征衍生、海量特征与特征筛选
关于有哪些可以用于特征衍生的方法，我们稍后会详细介绍。但这里需要注意的是，在这种尽可能衍生更多特征的的基本指导思想下，自动化批量特征衍生往往会创造出非常多的特征，而这些特征并不是每个都能帮助模型训练的出更好的结果，并且特征列本身过多也会极大程度上影响建模效率。例如，继续上面的例子，我们只需要对tenure字段进行独热编码就可以一次性衍生出73个列，而在随机选取tenure字段的两个不同值（例如tenure=15、17组合出的 C 73 2 = 73 ∗ 72 2 = 2628 C^2_{73}=\frac{73*72}{2}=2628 C732=273∗72=2628种特征中，大多数特征也属于无用特征。
因此若要进行自动批量特征衍生，往往是一定需要搭配特征筛选方法的，也就是需要借助一些策略，来对批量创建的海量特征进行筛选，“去粗取精”，选出最能提升模型效果的特征，在提高模型效果的同时提升建模效率。例如此前的IV值筛选特征就是一种特征筛选的方法，当然本小节我们先介绍关于自动化批量特征衍生的方法，下一小节我们再重点介绍更多特征筛选策略。
此外，批量特征衍生还将造成另外的一个问题，那就是很多衍生出来的特征并不具备业务层面的可解释性，例如tenure=15、17组合衍生出来的特征，我们就无法从业务的角度解释为何需要这么做，但是，这并不代表该特征就一定无法帮助模型训练得出一个更好的结果。在机器学习整体都是后验思想为主导的情况下，我们往往不会过于关注批量衍生的特征具体的业务含义，而只考虑最终的建模效果，也就是说，批量特征衍生+特征筛选的策略，完全是一个“依据建模结果说话”的策略。
- 特征衍生方法汇总
接下来我们将首先全面详细的介绍常用特征衍生方法，并重点讨论相关方法的实现代码，这里我们先考虑如何把特征“做多”，然后再考虑如何把特征“做精”。总的来说，批量特征衍生有如下方法划分：
- 本节学习过程注意事项
相比有严谨理论体系的机器学习算法，特征衍生的相关方法更像是人们在长期实践过程中总结出来的方法论，这些方法切实有效，但（暂时）却没有一套能够完整统一的理论体系来“框住”这些方法。因此特征衍生的方法很多时候都是“就方法讨论方法”，很多方法使用的技巧和注意事项也都是经验之谈。此外，由于特征衍生应用场景复杂多变，需要综合数据体量、数据规律、现有算力等因素进行考虑，截至目前也并没有统一的第三方库能够提供完整特征衍生的方法实现，因此本节每个特征衍生的方法介绍，我们都将从三个角度入手来进行讨论，分别是该方法的执行过程、使用时的注意事项以及实现代码。尤其需要注意的是，本节会提供所有常用特征衍生方法封装的函数，这些函数或简单或复杂，但都将被后续案例课长期反复复用，当然也可作为实际工作或参与竞赛时的有力工具，因此需要在学习时额外注重对本节代码的学习与掌握。
一、单变量特征衍生方法
正如此前在手动特征衍生过程中看到的那样，一般来说，我们可以借助单个变量进行特征衍生，也可以组合多个变量进行特征衍生，我们先看相对更简单的单变量特征衍生方法。
1.数据重编码特征衍生
首先需要知道的是，此前我们所介绍的所有数据重编码的过程，新创建的列都可以作为一个额外的独立特征，即我们在实际建模过程中，不一定是用重编码后新的列替换掉原始列，而是考虑同时保留新的特征和旧的特征，带入到下一个环节、即特征筛选来进行特征筛选，如果数据重编码后的特征是有效的，则自然会被保留，否则则会被剔除。
这么一来，我们或许就不用考虑在当前模型下是否需要进行数据重编码，而是无论是否需要，都先进行重编码、并同时保留原特征和衍生出来的新的特征。此处我们简单回顾此前所介绍的一系列数据重编码的方法：
- 连续变量数据重编码方法
- 标准化：0-1标准化/Z-Score标准化
- 离散化：等距分箱/等频分箱/聚类分箱
- 离散变量数据重编码方法
- 自然数编码/字典编码
- 独热编码/哑变量变换
当然，在同时保留原始列和重编码的列时，极有可能出现原始列和重编码的列都是有效特征的情况，例如此前我们看到的tenure独热编码后的某列（tenure=1）和原始列同时带入模型的情况。
2.高阶多项式特征衍生
对于单独的变量来说，除了可以通过重编码进行特征衍生外，还可以通过多项式进行特征衍生，即创建一些自身数据的二次方、三次方数据等。该方法我们曾在逻辑回归一节中重点介绍过，此处进行简单回顾。
- 多项式处理结果
假设 X 1 X1 X1是某原始特征，单独特征进行高阶多项式衍生过程如下：
- 多项式衍生实现方法
上述过程较为简单，直接利用数组广播特性，手动实现过程也较为简单。当然我们更推荐使用sklearn中的PolynomialFeatures评估器来实现该过程。该评估器不仅能够非常便捷的实现单变量的多项式衍生，也能够快速实现多变量组合多项式衍生，且能够与机器学习流集成，也便于后续的超参数搜索方法的使用。
from sklearn.preprocessing import PolynomialFeatures
x1 = np.array([1, 2, 4, 1, 3])
PolynomialFeatures(degree=5).fit_transform(x1.reshape(-1, 1))
#array([[1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00],
# [1.000e+00, 2.000e+00, 4.000e+00, 8.000e+00, 1.600e+01, 3.200e+01],
# [1.000e+00, 4.000e+00, 1.600e+01, 6.400e+01, 2.560e+02, 1.024e+03],
# [1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 1.000e+00],
# [1.000e+00, 3.000e+00, 9.000e+00, 2.700e+01, 8.100e+01, 2.430e+02]])
尽管过程简单，但多项式特征衍生也是极为常见且效果出色的特征衍生方法，在此前的逻辑回归建模实验中，简单的多项式衍生，就能够将逻辑回归的决策边界由线性改善至不规则边界，从而极大提升模型建模效果：
当然，一般来说单特征的多项式往往是针对连续变量会更有效，但再某些情况下也可以将其用于离散型随机变量。
3.特征衍生准则
- 无限特征
在上述过程的基础上，我们将这些方法稍作组合、或者是进行深入拓展，则会发现，就单独一个特征而言，我们都可以衍生出无限个特征。例如我们可以将某连续变量先进行N阶多项式衍生，然后再进行分箱，然后再进行独热编码；或者就是单纯的进行非常高阶的多项式衍生；再或者，我们看随机修改下归一化的规则（以0-1标准化为例），不再是减去最小值除以极值，而是减去次小的值、或者第三小的值等等。你会发现，哪怕是单独针对某个变量，我们都可以衍生出近乎无穷个特征。
但需要知道的是，尽管特征可以无限衍生，但因为算力有限、时间有限，我们不可能进行无止尽的尝试。因此，在实际模型训练过程中，也并非无节制的朝向无限特征的方向进行特征衍生，往往我们需要有些判断，即哪些情况下朝什么方向进行特征衍生是最有效的。当然，同时我们需要知道的是，特征衍生的方法极少有理论依据、或者只有零散的理论依据，例如多项式衍生其实是借助了核函数的思想，但就特征衍生的技术整体而言，并没有一个完整系统的理论体系，作为何时选择何种方法的参考依据。因此不难看出，特征衍生其实是一个极其考验建模工作者的建模经验、数据敏感度甚至是建模灵感的工作事项，而在很多实际工作和竞赛中，我们也确实会发现特征工程方法选择的不同，往往是建模结果拉开差距的关键。
随着课程的深入，我们还会发现，无限衍生特征的方向会有非常多，并且我们也会发现，随着特征衍生进行的深入，新特征的有效性也是在快速递减的。
而在茫茫多特征衍生方向中如何选择当前数据集特征衍生的方向，首先，课上会在每套特征衍生方法的后面附上这些方法的选择依据，这些依据大都源自实践经验，可以普遍适用于一般情况，并作为特征衍生的基本依据；其次，在后续的案例课中，我们也将结合具体的数据来讨论不同情况下最适用的特征衍生方法，在实践中快速积累特征衍生方法的使用经验。
- 特征衍生选择依据
这里我们先给出上述单变量特征衍生方法在使用过程中的选取依据，此处我们假设实际构建的模型以集成学习为主：
- 优先考虑分类变量的独热编码，并同时保留原始变量与独热编码衍生后的变量。独热编码能够丰富树模型生长过程中备选的数据集切分点，因此能够进一步丰富集成学习中不同树模型可能的差异性。但同时也需要注意的是有两种情况不适用于使用独热编码，其一是分类变量取值水平较多（例如超过10个取值），此时独热编码会造成特征矩阵过于稀疏，从而影响最终建模效果；其二则是如果该离散变量参与后续多变量的交叉衍生（稍后会介绍），则一般需再对单独单个变量进行独热编码；
- 优先考虑连续变量的数据归一化，尽管归一化不会改变数据集分布，即无法通过形式上的变换增加树生长的多样性，但归一化能够加快梯度下降的执行速度，加快迭代收敛的过程；
- 在连续变量较多的情况下，可以考虑对连续变量进行分箱，原因同第一点。具体分享方法优先考虑聚类分箱，若数据量过大，可以使用MiniBatch K-Means提高效率，或者也可以简化为等频率/等宽分箱；
- 不建议对单变量使用多项式衍生方法，相比单变量的多项式衍生，带有交叉项的多变量的多项式衍生往往效果会更好。
二、双变量特征衍生方法
接下来我们进一步介绍涉及多个变量的特征衍生方法。在大多数情况下，多个变量的交叉组合往往都比单变量特征衍生更有价值。而该过程我们在手动特征衍生时也见到了多次，例如我们创建的老年且经济不独立的标识字段、按月付费且无纸质合约类账户等，都是两个变量的交叉组合结果；而每位用户购买服务总数字段，则更是十个购买服务记录的字段求和之后的结果。一般来说如果具体细分的化，两个特征组合成新的字段我们会称其为双变量（或者双特征）交叉衍生，而如果涉及到多个字段组合，则会称其为多变量交叉衍生。一般来说，双变量特征衍生是目前常见特征衍生方法中最常见、同样也是效果最好的一类方法，这也是我们接下来要重点介绍的方法。而多变量特征衍生，除了四则运算（尤其以加法居多）的组合方法外，其他衍生方法随着组合的字段增加往往会伴随非常严重的信息衰减，因此该类方法除特定场合外一般不会优先考虑使用。我们会在介绍完双变量衍生方法后再介绍多变量衍生。
接下来开始介绍双变量特征衍生方法，本部分我们会以各个不同的方法作为主线进行介绍，并在每个方法后介绍该方法的使用场景。
1.四则运算特征衍生
先从简单的方法开始讨论——四则运算特征衍生。该过程非常简单，就是单纯的选取两列进行四则运算，基本过程如下：
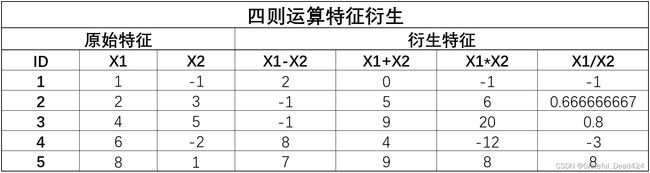
该过程并不复杂，实际代码执行过程也只需要单独索引出两列然后进行四则运算即可。一般来说，四则运算特征衍生的使用场景较为固定，主要有以下三个：
- 其一是用于创建业务补充字段：在某些数据集中，我们需要通过四则运算来创建具有明显业务含义的补充字段，例如在上述电信用户流失数据集中，我们可以通过将总消费金额除以用户入网时间，即可算出用户平均每月的消费金额，或者使用用户每月消费金额除以购买服务总数，则可算出每项服务的平均价格，这些字段有明确的业务含义，我们甚至可以将其视作原始字段；
- 其二，往往在特征衍生的所有工作结束后，我们会就这一系列衍生出来的新字段进行四则运算特征衍生，作为数据信息的一种补充；
- 其三，在某些极为特殊的字段创建过程中使用，例如竞赛中常用的黄金组合特征、流量平滑特征（稍后会重点讨论）等，需要使用四则运算进行特征衍生。
2.交叉组合特征衍生
- 方法介绍
所谓交叉组合特征衍生，指的是不同分类变量不同取值水平之间进行交叉组合，从而创建新字段的过程。例如此前我们创建的老年且经济不独立的标识字段，实际上就是是否是老年人字段（SeniorCitizen）和是否经济独立字段（Dependents）两个字段交叉组合衍生过程中的一个：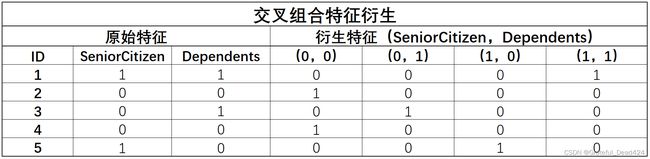
不难看出，该计算流程并不复杂，需要注意的是，交叉组合后衍生的特征个数是参数交叉组合的特征的取值水平之积，因此交叉组合特征衍生一般只适用于取值水平较少的分类变量之间进行，若是分类变量或者取值水平较多的离散变量彼此之间进行交叉组合，则会导致衍生特征矩阵过于稀疏，从而无法为模型提供有效的训练信息。
- 手动实现
我们仍然以telco数据集为例，尝试围绕’SeniorCitizen’、‘Partner’、'Dependents’字段进行两两交叉组合衍生，当然该流程也可以顺利推广至任意多个任意取值个数的分类变量两两交叉组合衍生过程。
# 数据集中离散变量
category_cols
#['gender',
# 'SeniorCitizen',
# 'Partner',
# 'Dependents',
# 'PhoneService',
# 'MultipleLines',
# 'InternetService',
# 'OnlineSecurity',
# 'OnlineBackup',
# 'DeviceProtection',
# 'TechSupport',
# 'StreamingTV',
# 'StreamingMovies',
# 'Contract',
# 'PaperlessBilling',
# 'PaymentMethod']
# 提取目标字段
colNames = ['SeniorCitizen', 'Partner', 'Dependents']
# 单独提取目标字段的数据集
features_temp = features[colNames]
features_temp.head(5)
# 创建空列表用于存储衍生后的特征名称和特征
colNames_new_l = []
features_new_l = []
# enumerate过程
for col_index, col_name in enumerate(colNames):
print(col_index, col_name)
#0 SeniorCitizen
#1 Partner
#2 Dependents
# 衍生特征列名称
for col_index, col_name in enumerate(colNames):
for col_sub_index in range(col_index+1, len(colNames)):
newNames = col_name + '&' + colNames[col_sub_index]
print(newNames)
#SeniorCitizen&Partner
#SeniorCitizen&Dependents
#Partner&Dependents
# 创建衍生特征列名称及特征本身
for col_index, col_name in enumerate(colNames):
for col_sub_index in range(col_index+1, len(colNames)):
newNames = col_name + '&' + colNames[col_sub_index]
colNames_new_l.append(newNames)
newDF = pd.Series(features[col_name].astype('str')
+ '&'
+ features[colNames[col_sub_index]].astype('str'),
name=col_name)
features_new_l.append(newDF)
features_new = pd.concat(features_new_l, axis=1)
features_new.columns = colNames_new_l
features_new
colNames_new_l
#['SeniorCitizen&Partner', 'SeniorCitizen&Dependents', 'Partner&Dependents']
截至目前，我们创建了3个4分类的变量，我们可以直接将其带入进行建模，但需要知道的是这些四分类变量并不是有序变量，因此往往我们需要进一步将这些衍生的变量进行独热编码，然后再带入模型：
enc = preprocessing.OneHotEncoder()
enc.fit_transform(features_new)
def cate_colName(Transformer, category_cols, drop='if_binary'):
"""
离散字段独热编码后字段名创建函数
:param Transformer: 独热编码转化器
:param category_cols: 输入转化器的离散变量
:param drop: 独热编码转化器的drop参数
"""
cate_cols_new = []
col_value = Transformer.categories_
for i, j in enumerate(category_cols):
if (drop == 'if_binary') & (len(col_value[i]) == 2):
cate_cols_new.append(j)
else:
for f in col_value[i]:
feature_name = j + '_' + f
cate_cols_new.append(feature_name)
return(cate_cols_new)
# 借助此前定义的列名称提取器进行列名称提取
cate_colName(enc, colNames_new_l, drop=None)
#['SeniorCitizen&Partner_0&No',
# 'SeniorCitizen&Partner_0&Yes',
# 'SeniorCitizen&Partner_1&No',
# 'SeniorCitizen&Partner_1&Yes',
# 'SeniorCitizen&Dependents_0&No',
# 'SeniorCitizen&Dependents_0&Yes',
# 'SeniorCitizen&Dependents_1&No',
# 'SeniorCitizen&Dependents_1&Yes',
# 'Partner&Dependents_No&No',
# 'Partner&Dependents_No&Yes',
# 'Partner&Dependents_Yes&No',
# 'Partner&Dependents_Yes&Yes']
# 最后创建一个完整的衍生后的特征矩阵
features_new_af = pd.DataFrame(enc.fit_transform(features_new).toarray(),
columns = cate_colName(enc, colNames_new_l, drop=None))
features_new_af.head(5)
features_new_af.shape
#(7043, 12)
3*4=12
至此，我们就完整的完成了既定变量的两两交叉衍生过程，我们可以将上述过程封装为如下函数：
- 函数封装
def Binary_Cross_Combination(colNames, features, OneHot=True):
"""
分类变量两两组合交叉衍生函数
:param colNames: 参与交叉衍生的列名称
:param features: 原始数据集
:param OneHot: 是否进行独热编码
:return：交叉衍生后的新特征和新列名称
"""
# 创建空列表存储器
colNames_new_l = []
features_new_l = []
# 提取需要进行交叉组合的特征
features = features[colNames]
# 逐个创造新特征名称、新特征
for col_index, col_name in enumerate(colNames):
for col_sub_index in range(col_index+1, len(colNames)):
newNames = col_name + '&' + colNames[col_sub_index]
colNames_new_l.append(newNames)
newDF = pd.Series(features[col_name].astype('str')
+ '&'
+ features[colNames[col_sub_index]].astype('str'),
name=col_name)
features_new_l.append(newDF)
# 拼接新特征矩阵
features_new = pd.concat(features_new_l, axis=1)
features_new.columns = colNames_new_l
colNames_new = colNames_new_l
# 对新特征矩阵进行独热编码
if OneHot == True:
enc = preprocessing.OneHotEncoder()
enc.fit_transform(features_new)
colNames_new = cate_colName(enc, colNames_new_l, drop=None)
features_new = pd.DataFrame(enc.fit_transform(features_new).toarray(), columns=colNames_new)
return features_new, colNames_new
这里需要注意，本节定义的特征衍生函数都将创建衍生列的特征名称，同时输出的数据也是衍生后的新的特征矩阵，而非和原数据拼接后的结果，这也将为后续使用多种方法、创建多个衍生特征矩阵、再进行统一拼接提供便捷。
简单验证上述函数执行过程：
features_new, colNames_new = Binary_Cross_Combination(colNames, features)
features_new.shape
#(7043, 12)
features_new.head(5)
colNames_new
#['SeniorCitizen&Partner_0&No',
# 'SeniorCitizen&Partner_0&Yes',
# 'SeniorCitizen&Partner_1&No',
# 'SeniorCitizen&Partner_1&Yes',
# 'SeniorCitizen&Dependents_0&No',
# 'SeniorCitizen&Dependents_0&Yes',
# 'SeniorCitizen&Dependents_1&No',
# 'SeniorCitizen&Dependents_1&Yes',
# 'Partner&Dependents_No&No',
# 'Partner&Dependents_No&Yes',
# 'Partner&Dependents_Yes&No',
# 'Partner&Dependents_Yes&Yes']
当然，完成衍生特征矩阵创建后，还需要和原始数据集进行拼接，此处拼接过程较为简单，直接使用concat函数即可：
df_temp = pd.concat([features, features_new], axis=1)
df_temp.head(5)
至此，我们就完成了双变量交叉组合衍生的全过程。这里我们不着急带入新的特征进入模型进行效果测试，对于大多数批量创建特征的方法来说，创建的海量特征往往无效特征占绝大多数，例如此前我们曾手动验证过老年无伴侣字段就是无效字段。因此，如果不配合特征筛选方法、盲目带入大量无用特征进入模型，不仅不会起到正向的提升效果，往往可能还会适得其反。待后续介绍特征筛选方法后，我们再来看这些衍生出来的特征效用如何。
- 使用时注意事项
在实际使用过程中，双变量的交叉衍生是最常见的特征衍生方法，也是第一梯队优先考虑的特征衍生的策略。通过不同分类水平的交叉衍生，能够极大程度丰富数据集信息呈现形式，同时也为有效信息的精细化筛选提供了更多可能。
但同时也需要注意，越多的分类特征进行交叉组合、或者参与交叉组合的特征本身分类水平更多，衍生的特征数量也将指数级上涨，例如有10个二分类变量参与交叉衍生，则最终将衍生出 2 10 = 1024 2^{10}=1024 210=1024个新特征，而如果是10个三分类变量参与交叉衍生，则最终将衍生出 3 10 = 29049 3^{10}=29049 310=29049个新特征。无论如何进行衍生，首先我们需要对衍生后的特征规模有基本判断。
3.分组统计特征衍生
- 方法介绍
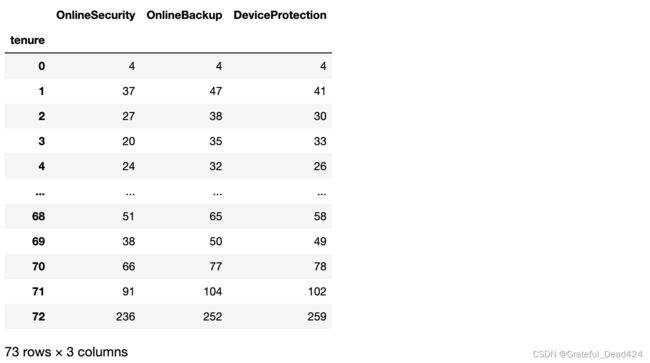
接下来，我们继续讨论另一种同样非常常用的特征衍生方法：分组统计特征衍生方法。所谓分组统计，顾名思义，就是A特征根据B特征的不同取值进行分组统计，统计量可以是均值、方差等针对连续变量的统计指标，也可以是众数、分位数等针对离散变量的统计指标，例如我们可以计算不同入网时间用户的平均月消费金额、消费金额最大值、消费金额最小值等，基本过程如下：
同样，该过程也并不复杂，在实际执行分组统计特征衍生的过程中（假设是A特征根据B特征的不同取值进行分组统计），有以下几点需要注意：
-
首先，一般来说A特征可以是离散变量也可以是连续变量，而B特征必须是离散变量，且最好是一些取值较多的离散变量（或者固定取值的连续变量），例如本数据集中的tenure字段，总共有73个取值。主要原因是如果B特征取值较少，则在衍生的特征矩阵中会出现大量的重复的行；
-
其次，在实际计算A的分组统计量时，可以不局限于连续特征只用连续变量的统计量、离散特征只用离散的统计量，完全可以交叉使用，例如A是离散变量，我们也可以分组统计其均值、方差、偏度、峰度等，连续变量也可以统计众数、分位数等。很多时候，更多的信息组合有可能会带来更多的可能性；
-
其三，有的时候分组统计还可以用于多表连接的场景，例如假设现在给出的数据集不是每个用户的汇总统计结果，而是每个用户在过去的一段时间内的行为记录，则我们可以根据用户ID对其进行分组统计汇总：
-
其四，很多时候我们还会考虑进一步围绕特征A和分组统计结果进行再一次的四则运算特征衍生，例如用月度消费金额减去分组均值，则可以比较每一位用户与相同时间入网用户的消费平均水平的差异，围绕衍生特征再次进行衍生，我们将其称为统计演变特征，也是分组汇总衍生特征的重要应用场景：
-
手动实现
接下来我们考虑分组汇总特征如何实现。这里我们可以优先考虑借助Pandas中的groupby方法来实现，首先简单回归groupby方法的基本使用，这里我们提取’tenure’、‘SeniorCitizen’、'MonthlyCharges’三列来尝试进行单列聚合和多列聚合：
# 提取目标字段
colNames = ['tenure', 'SeniorCitizen', 'MonthlyCharges']
# 单独提取目标字段的数据集
features_temp = features[colNames]
features_temp
# 在不同tenure取值下计算其他变量分组均值的结果
features_temp.groupby('tenure').mean()
# 在不同tenure取值下计算其他变量分组标准差的结果
features_temp.groupby('tenure').std()
此外，我们还可以尝试多列聚合
# 在'tenure'、'SeniorCitizen'交叉取值分组下，计算组内月度消费金额均值
features_temp.groupby(['tenure', 'SeniorCitizen']).mean()
当然，groupby也支持同时输入多个统计量进行汇总计算，此时推荐使用agg方法来进行相关操作:
colNames
#['tenure', 'SeniorCitizen', 'MonthlyCharges']
# 分组汇总字段
colNames_sub = ['SeniorCitizen', 'MonthlyCharges']
# 创建空字典
aggs = {}
# 字段汇总统计量设置
for col in colNames_sub:
aggs[col] = ['mean', 'min', 'max']
# 每个字段汇总统计信息
aggs
#{'SeniorCitizen': ['mean', 'min', 'max'],
# 'MonthlyCharges': ['mean', 'min', 'max']}
# 创建新的列名称
cols = ['tenure']
for key in aggs.keys():
cols.extend([key+'_'+'tenure'+'_'+stat for stat in aggs[key]])
cols
#['tenure',
# 'SeniorCitizen_tenure_mean',
# 'SeniorCitizen_tenure_min',
# 'SeniorCitizen_tenure_max',
# 'MonthlyCharges_tenure_mean',
# 'MonthlyCharges_tenure_min',
# 'MonthlyCharges_tenure_max']
而这里的列表表达式，返回结果如下：
[key+'_'+'tenure'+'_'+stat for stat in aggs[key]]
#['MonthlyCharges_tenure_mean',
# 'MonthlyCharges_tenure_min',
# 'MonthlyCharges_tenure_max']
这也是为何使用extend方法的原因。接下来我们创建新特征：
features_new = features_temp.groupby('tenure').agg(aggs).reset_index()
features_new.head(5)
features_new = features_temp.groupby('tenure').agg(aggs).reset_index()
features_new.head(5)
# 重新设置列名称
features_new.columns = cols
features_new
当然，在创建完统计汇总信息后，还需要以tenure为主键和原始数据集进行拼接，此时需要使用merge函数进行操作：
df_temp = pd.merge(features, features_new, how='left',on='tenure')
df_temp.head()
len(df_temp.SeniorCitizen_tenure_mean.unique())
#69
- 常用统计量补充
这里我们对所有分组统计过程中可能用到的统计量进行汇总，需要注意的是，在进行分组汇总统计时，我们往往会无差别的进行尽可能多的统计量进行计算，只在针对离散或连续变量时进行统计量设置的些许调整。可用于连续性变量的统计量如下：
- mean/var：均值、方差；
- max/min：最大值、最小值；
- skew：数据分布偏度，小于零时左偏，大于零时右偏；
a = np.array([[1, 2, 3, 2, 5, 1], [0, 0, 0, 1, 1, 1]])
df = pd.DataFrame(a.T, columns=['x1', 'x2'])
df
aggs = {'x1': ['mean', 'var', 'max', 'min', 'skew']}
df.groupby('x2').agg(aggs).reset_index()
常用的分类变量的统计量如下，当然除了偏度外，其他连续变量的统计量也是可用于分类变量的：
- median：中位数；
- count：个数统计；
- nunique：类别数；
- quantile：分位数
df = pd.DataFrame({'x1':[1, 3, 4, 2, 1], 'x2':[0, 0, 1, 1, 1]})
df
aggs = {'x1': ['median', 'count', 'nunique']}
df.groupby('x2').agg(aggs).reset_index()
而对于分位数的计算，则需要借助自定义函数来完成计算：
def q1(x):
"""
下四分位数
"""
return x.quantile(0.25)
def q2(x):
"""
上四分位数
"""
return x.quantile(0.75)
d1 = pd.DataFrame({'x1':[3, 2, 4, 4, 2, 2], 'x2':[0, 1, 1, 0, 0, 0]})
d1
aggs = {'x1': [q1, q2]}
d2 = d1.groupby('x2').agg(aggs).reset_index()
d2
d2.columns = ['x2', 'x1_x2_q1', 'x1_x2_q2']
d2
当然，分位数也是可以应用于连续变量的。
最后，让我们来汇总各种不同类型的变量可以使用的统计量。正如此前讨论的，分位数可以用于连续变量，而连续变量的统计指标中只有偏度不适用于离散变量。据此我们在划分连续变量和分类变量后，可以设置如下基本统计衍生指标：
aggs_num = {'num': ['mean', 'var', 'max', 'min', 'skew', 'median', 'q1', 'q2']}
aggs_cat = {'cat': ['mean', 'var', 'max', 'min', 'median', 'count', 'nunique', 'q1', 'q2']}
需要注意的是，上面的统计指标设置只适用于一般情况，在某些情况下，如连续变量取值个数较少（只有十几个或者几十个不同取值）时，该连续变量也可以使用’count’、'nunique’等指标，而如果分类变量取值个数较多（如超过5个），则也可以使用偏度计算公式，具体如何选择还需要视具体情况而定。
- 函数封装
针对此一般情况，我们可以将分组统计特征衍生过程封装为如下函数。在实际封装时需要注意，若是使用自定义的q1、q2函数，则aggs字典在辅助定义列名称时value需要以字符串形式出现，而在作为参数带入到agg方法中时则需要以函数名称出现，因此需要重复定义两次aggs：
# x2在x1上分组汇总
colNames = ['x2']
keyCol = 'x1'
接下来是第一次定义aggs，用于辅助定义列名称：
aggs = {}
for col in colNames:
aggs[col] = ['q1', 'q2']
aggs
#{'x2': ['q1', 'q2']}
# 新增列的列名称
cols = [keyCol]
for key in aggs.keys():
cols.extend([key+'_'+keyCol+'_'+stat for stat in aggs[key]])
cols
#['x1', 'x2_x1_q1', 'x2_x1_q2']
第二次定义aggs，用于配合groupby过程进行分组计算：
aggs = {}
for col in colNames:
aggs[col] = [q1, q2]
aggs
#{'x2': [, ]}
aggs = {}
for col in colNames:
aggs[col] = [ q1, q2]
d2 = d1.groupby(keyCol).agg(aggs).reset_index()
d2
d2.columns = cols
d2
接下来，我们进行函数封装。为了能够更好的适用于不同情况，该函数需要单独输入连续变量和离散变量，同时也可以自定义不同类别变量分组统计的统计量：
def Binary_Group_Statistics(keyCol,
features,
col_num=None,
col_cat=None,
num_stat=['mean', 'var', 'max', 'min', 'skew', 'median'],
cat_stat=['mean', 'var', 'max', 'min', 'median', 'count', 'nunique'],
quant=True):
"""
双变量分组统计特征衍生函数
:param keyCol: 分组参考的关键变量
:param features: 原始数据集
:param col_num: 参与衍生的连续型变量
:param col_cat: 参与衍生的离散型变量
:param num_stat: 连续变量分组统计量
:param cat_num: 离散变量分组统计量
:param quant: 是否计算分位数
:return：交叉衍生后的新特征和新特征的名称
"""
# 当输入的特征有连续型特征时
if col_num != None:
aggs_num = {}
colNames = col_num
# 创建agg方法所需字典
for col in col_num:
aggs_num[col] = num_stat
# 创建衍生特征名称列表
cols_num = [keyCol]
for key in aggs_num.keys():
cols_num.extend([key+'_'+keyCol+'_'+stat for stat in aggs_num[key]])
# 创建衍生特征df
features_num_new = features[col_num+[keyCol]].groupby(keyCol).agg(aggs_num).reset_index()
features_num_new.columns = cols_num
# 当输入的特征有连续型也有离散型特征时
if col_cat != None:
aggs_cat = {}
colNames = col_num + col_cat
# 创建agg方法所需字典
for col in col_cat:
aggs_cat[col] = cat_stat
# 创建衍生特征名称列表
cols_cat = [keyCol]
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+keyCol+'_'+stat for stat in aggs_cat[key]])
# 创建衍生特征df
features_cat_new = features[col_cat+[keyCol]].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
# 合并连续变量衍生结果与离散变量衍生结果
df_temp = pd.merge(features_num_new, features_cat_new, how='left',on=keyCol)
features_new = pd.merge(features[keyCol], df_temp, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_num + cols_cat
colNames_new.remove(keyCol)
colNames_new.remove(keyCol)
# 当只有连续变量时
else:
# merge连续变量衍生结果与原始数据，然后删除重复列
features_new = pd.merge(features[keyCol], features_num_new, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_num
colNames_new.remove(keyCol)
# 当没有输入连续变量时
else:
# 但存在分类变量时，即只有分类变量时
if col_cat != None:
aggs_cat = {}
colNames = col_cat
for col in col_cat:
aggs_cat[col] = cat_stat
cols_cat = [keyCol]
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+keyCol+'_'+stat for stat in aggs_cat[key]])
features_cat_new = features[col_cat+[keyCol]].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
features_new = pd.merge(features[keyCol], features_cat_new, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols_cat
colNames_new.remove(keyCol)
if quant:
# 定义四分位计算函数
def q1(x):
"""
下四分位数
"""
return x.quantile(0.25)
def q2(x):
"""
上四分位数
"""
return x.quantile(0.75)
aggs = {}
for col in colNames:
aggs[col] = ['q1', 'q2']
cols = [keyCol]
for key in aggs.keys():
cols.extend([key+'_'+keyCol+'_'+stat for stat in aggs[key]])
aggs = {}
for col in colNames:
aggs[col] = [q1, q2]
features_temp = features[colNames+[keyCol]].groupby(keyCol).agg(aggs).reset_index()
features_temp.columns = cols
features_new = pd.merge(features_new, features_temp, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = colNames_new + cols
colNames_new.remove(keyCol)
features_new.drop([keyCol], axis=1, inplace=True)
return features_new, colNames_new
这里需要注意merge过程的一个小技巧，如果我们希望函数创建的衍生特征矩阵不包含原始特征列的话，可以在merge的过程中主表只保留主键的那一列：
d1 = pd.DataFrame({'tenure':[1, 2, 1, 3, 2, 3], 'x1':[2, 5, 1, 2, 6, 1]})
d1
d2 = pd.DataFrame({'tenure':[1, 2, 3], 'stat':[1, 7, 4]})
d2
pd.merge(d1['tenure'], d2, how='left',on='tenure')
接下来在完整数据集上测试效果：
col_num = ['MonthlyCharges']
col_cat = ['SeniorCitizen']
keyCol = 'tenure'
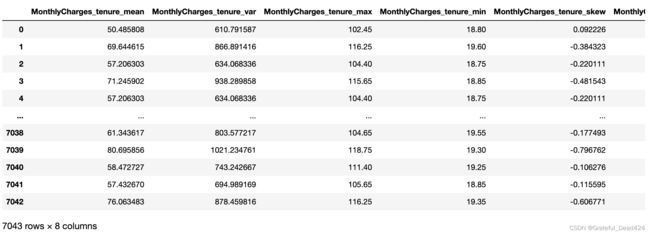
df, col = Binary_Group_Statistics(keyCol, features, col_num, col_cat)
df.head(5)
col
#['MonthlyCharges_tenure_mean',
# 'MonthlyCharges_tenure_var',
# 'MonthlyCharges_tenure_max',
# 'MonthlyCharges_tenure_min',
# 'MonthlyCharges_tenure_skew',
# 'MonthlyCharges_tenure_median',
# 'SeniorCitizen_tenure_mean',
# 'SeniorCitizen_tenure_var',
# 'SeniorCitizen_tenure_max',
# 'SeniorCitizen_tenure_min',
# 'SeniorCitizen_tenure_median',
# 'SeniorCitizen_tenure_count',
# 'SeniorCitizen_tenure_nunique',
# 'MonthlyCharges_tenure_q1',
# 'MonthlyCharges_tenure_q2',
# 'SeniorCitizen_tenure_q1',
# 'SeniorCitizen_tenure_q2']
df.columns
#Index(['MonthlyCharges_tenure_mean', 'MonthlyCharges_tenure_var',
# 'MonthlyCharges_tenure_max', 'MonthlyCharges_tenure_min',
# 'MonthlyCharges_tenure_skew', 'MonthlyCharges_tenure_median',
# 'SeniorCitizen_tenure_mean', 'SeniorCitizen_tenure_var',
# 'SeniorCitizen_tenure_max', 'SeniorCitizen_tenure_min',
# 'SeniorCitizen_tenure_median', 'SeniorCitizen_tenure_count',
# 'SeniorCitizen_tenure_nunique', 'MonthlyCharges_tenure_q1',
# 'MonthlyCharges_tenure_q2', 'SeniorCitizen_tenure_q1',
# 'SeniorCitizen_tenure_q2'],
# dtype='object')
一般来说在进行分组统计时，需要注意某些统计指标在计算过程中可能造成缺失值，需要在执行完特征衍生后再进行缺失值查找：
df.isnull().sum()
#MonthlyCharges_tenure_mean 0
#MonthlyCharges_tenure_var 0
#MonthlyCharges_tenure_max 0
#MonthlyCharges_tenure_min 0
#MonthlyCharges_tenure_skew 0
#MonthlyCharges_tenure_median 0
#SeniorCitizen_tenure_mean 0
#SeniorCitizen_tenure_var 0
#SeniorCitizen_tenure_max 0
#SeniorCitizen_tenure_min 0
#SeniorCitizen_tenure_median 0
#SeniorCitizen_tenure_count 0
#SeniorCitizen_tenure_nunique 0
#MonthlyCharges_tenure_q1 0
#MonthlyCharges_tenure_q2 0
#SeniorCitizen_tenure_q1 0
#SeniorCitizen_tenure_q2 0
#dtype: int64
当然，我们可以进一步测试，如果只输入一个连续字段进行分组统计衍生时函数效果：
col_num = ['MonthlyCharges']
df, col = Binary_Group_Statistics(keyCol, features, col_num)
df.head(5)
至此，我们就完整讨论了分组统计特征衍生的相关方法。
4.多项式特征衍生
- 方法介绍
当然，双变量的多项式衍生会比单变量多项式衍生更有效果，该过程并不复杂，只是在单变量多项式衍生基础上增加了交叉项的计算，例如X1和X2都是某连续变量，在进行双变量二阶多项式衍生时计算过程如下：
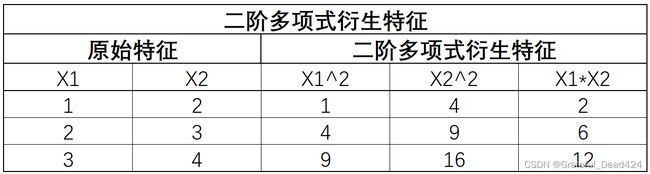
更高阶的多项式衍生过程也依此类推。在实际使用过程中，有以下几点注意事项：
-
一般来说双变量多项式衍生只适用于两个连续变量之间，一个连续变量一个离散变量或者两个离散变量进行多项式衍生意义不大（除非类似tenure字段，离散字段带有非常多不同的取值）；
-
在选取特征进行多项式衍生的过程中，往往我们不会随意组合连续变量来进行多项式衍生，而是只针对我们判断非常重要的特征来进行多项式衍生。就这点而言，多项式衍生和四则运算衍生非常类似，其使用场景背后的基本思路也完全一致：强化重要特征的表现形式；
-
关于衍生多少阶，一般来说伴随着多项式阶数的增加，各列数值也会呈现指数级递增（或递减），因此往往我们只会衍生3阶左右，极少数情况会衍生5-10阶。而伴随着多项式阶数的增加，也需要配合一些手段来消除数值绝对值爆炸或者衰减所造成的影响，例如对数据进行归一化处理等；
-
实现过程
而多项式衍生的实现过程也并不复杂，我们可以直接调用sklearn中的PolynomialFeatures来执行相关操作：
from sklearn.preprocessing import PolynomialFeatures
df = pd.DataFrame({'X1':[1, 2, 3], 'X2':[2, 3, 4]})
df
PolynomialFeatures(degree=2, include_bias=False).fit_transform(df)
#array([[ 1., 2., 1., 2., 4.],
# [ 2., 3., 4., 6., 9.],
# [ 3., 4., 9., 12., 16.]])
PolynomialFeatures评估器的使用并不复杂，重点需要关注以下两个参数：
- interaction_only：默认False，如果选择为True，则表示只创建交叉项；
- include_bias：默认为True，即考虑计算特征的0次方，除了需要人工捕捉截距，否则建议修改为False。全是1的列不包含任何有效信息；
而如果进一步考虑衍生特征的排列顺序，在默认情况下PolynomialFeatures，二阶多项式衍生后的特征排布如下：
即按照第一个变量阶数依次递减、第二个变量阶数依次递增来进行排布，首先是 X 1 2 ∗ X 2 0 X_1^2 * X_2^0 X12∗X20，然后是 X 1 1 ∗ X 2 1 X_1^1*X_2^1 X11∗X21，然后是 X 1 0 ∗ X 2 2 X_1^0*X_2^2 X10∗X22。如果是三阶多项式衍生也是类似
PolynomialFeatures(degree=3, include_bias=False).fit_transform(df)
#array([[ 1., 2., 1., 2., 4., 1., 2., 4., 8.],
# [ 2., 3., 4., 6., 9., 8., 12., 18., 27.],
# [ 3., 4., 9., 12., 16., 27., 36., 48., 64.]])
据此，我们可以在PolynomialFeatures过程外再嵌套一个函数，使得能够在创建新的特征的同时，创建新的列的名称。该函数最重要同时也是较为复杂的部分就是根据上述规则创建各衍生特征的名称，其基本过程如下：
# 创建数据集
df = pd.DataFrame({'X1':[1, 2, 3], 'X2':[2, 3, 4], 'X3':[1, 0, 0]})
df
# 选取X1、X2进行三阶衍生
colNames = ['X1', 'X2']
degree = 3
colNames_l = []
可以通过如下循环创建三阶多项式衍生时各衍生特征的列名称，当然，该循环也同样适用于更高阶的多项式衍生结果：
for deg in range(2, degree+1):
for i in range(deg+1):
col_temp = colNames[0] + '**' + str(deg-i) + '*'+ colNames[1] + '**' + str(i)
colNames_l.append(col_temp)
colNames_l
#['X1**2*X2**0',
# 'X1**1*X2**1',
# 'X1**0*X2**2',
# 'X1**3*X2**0',
# 'X1**2*X2**1',
# 'X1**1*X2**2',
# 'X1**0*X2**3']
上述过程可以封装为如下函数：
def Binary_PolynomialFeatures(colNames, degree, features):
"""
连续变量两变量多项式衍生函数
:param colNames: 参与交叉衍生的列名称
:param degree: 多项式最高阶
:param features: 原始数据集
:return：交叉衍生后的新特征和新列名称
"""
# 创建空列表存储器
colNames_new_l = []
features_new_l = []
# 提取需要进行多项式衍生的特征
features = features[colNames]
# 逐个进行多项式特征组合
for col_index, col_name in enumerate(colNames):
for col_sub_index in range(col_index+1, len(colNames)):
col_temp = [col_name] + [colNames[col_sub_index]]
array_new_temp = PolynomialFeatures(degree=degree, include_bias=False).fit_transform(features[col_temp])
features_new_l.append(pd.DataFrame(array_new_temp[:, 2:]))
# 逐个创建衍生多项式特征的名称
for deg in range(2, degree+1):
for i in range(deg+1):
col_name_temp = col_temp[0] + '**' + str(deg-i) + '*'+ col_temp[1] + '**' + str(i)
colNames_new_l.append(col_name_temp)
# 拼接新特征矩阵
features_new = pd.concat(features_new_l, axis=1)
features_new.columns = colNames_new_l
colNames_new = colNames_new_l
return features_new, colNames_new
简单检测函数效果，我们先带入两个特征进行计算：
features_new, colNames_new = Binary_PolynomialFeatures(colNames=colNames, degree=degree, features=df)
features_new
colNames_new
#['X1**2*X2**0',
# 'X1**1*X2**1',
# 'X1**0*X2**2',
# 'X1**3*X2**0',
# 'X1**2*X2**1',
# 'X1**1*X2**2',
# 'X1**0*X2**3']
然后再测试输入多个特征进行两两组合多项式计算：
colNames = ['X1', 'X2', 'X3']
features_new, colNames_new = Binary_PolynomialFeatures(colNames=colNames, degree=degree, features=df)
features_new
colNames_new
#['X1**2*X2**0',
# 'X1**1*X2**1',
# 'X1**0*X2**2',
# 'X1**3*X2**0',
# 'X1**2*X2**1',
# 'X1**1*X2**2',
# 'X1**0*X2**3',
# 'X1**2*X3**0',
# 'X1**1*X3**1',
# 'X1**0*X3**2',
# 'X1**3*X3**0',
# 'X1**2*X3**1',
# 'X1**1*X3**2',
# 'X1**0*X3**3',
# 'X2**2*X3**0',
# 'X2**1*X3**1',
# 'X2**0*X3**2',
# 'X2**3*X3**0',
# 'X2**2*X3**1',
# 'X2**1*X3**2',
# 'X2**0*X3**3']
至此，我们就完成了双变量的多项式特征衍生方法梳理。
5.统计演变特征
- 二阶特征衍生
一种很自然的联想，是当我们已经完成了一些特征衍生后，还会考虑以衍生特征为基础，进一步进行特征衍生，这也就是所谓的二阶特征衍生（注意区分二阶多项式衍生）。当然这个过程可以无限重复，这也是此前讨论为何会出现无限特征的根本原因之一。不过，在大多数情况下，二阶甚至是更高阶的特征衍生（以下简称高阶特征衍生）往往伴随着严重的信息衰减，大多数高阶衍生出来的特征其本身的有效性也将急剧下降，外加高阶特征衍生是在已有的大量衍生出来的一阶特征基础上再进行衍生，其计算过程往往需要消耗巨大的计算量，外加需要从一系列高阶衍生特征中挑选出极个别有用的特征也较为繁琐，因此，高阶衍生往往性价比较低，除非特殊情况，否则并不建议在广泛特征基础上进行大量高阶特征衍生的尝试。
- 统计演变特征
当然，尽管并不建议手动进行尝试，但在长期的实践过程中，人们还是总结出某些高阶衍生特征（主要是二阶衍生特征）在很多情况下都能起到很好的效果。需要注意的是，这里的着重指的是一些特征，而不是特征衍生的策略。在这些普遍有效的高阶特征中，最著名的就是所谓的统计演变特征，这些特征由原始特征和分组统计特征、或分组统计特征彼此之间交叉衍生而来，在很多算法竞赛和企业应用中，都被证明了有较高的尝试价值。
接下来我们就对这些统计演变特征进行逐一介绍。
5.1 原始特征与分组汇总特征交叉衍生
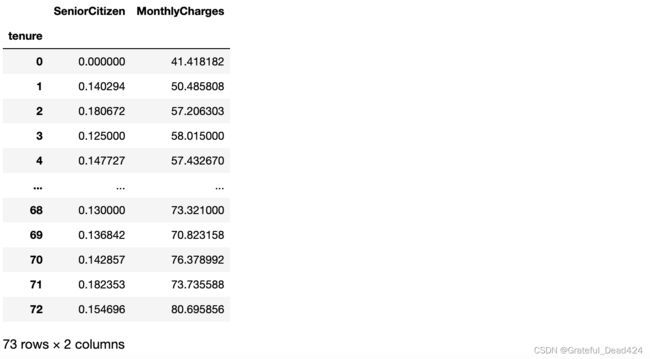
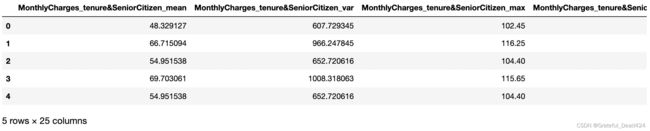
在统计演变特征中，最常用的特征衍生方法就是利用KeyCol和分组统计衍生特征进行交叉衍生，例如此前数据集分组统计汇总衍生为例，此处我们以tenure作为分组依据，对月均消费金额进行分组汇总统计，有计算结果如下：
col_num = ['MonthlyCharges']
df, col = Binary_Group_Statistics(keyCol, features, col_num)
df
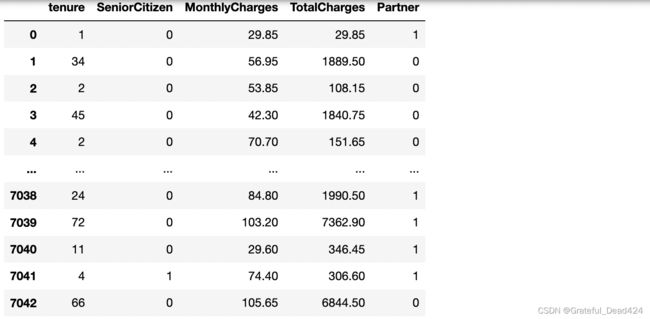
a = features.groupby("tenure").mean()
a
pd.merge(features,a,on="tenure",how="left")
我们依此为依据，可以进一步构建下列统计演变特征：
- 流量平滑特征
该特征通过KeyCol除以分组汇总均值后的特征计算而来，也就是利用tenure除以MonthlyCharges_tenure_mean计算得出。当然因为是进行除法运算，为了避免分母为零的情况，我们可以在分母位上加上一个很小的数，具体计算过程如下：
df['tenure'] / (df['MonthlyCharges_tenure_mean'] + 1e-5)
#0 0.019808
#1 0.488193
#2 0.034961
#3 0.631615
#4 0.034961
# ...
#7038 0.391239
#7039 0.892239
#7040 0.188122
#7041 0.069647
#7042 0.867696
#Length: 7043, dtype: float64
- 黄金组合特征
所谓黄金组合特征，就是简单的利用tenure减去MonthlyCharges_tenure_mean计算得出：
df['tenure'] - df['MonthlyCharges_tenure_mean']
#0 -49.485808
#1 -35.644615
#2 -55.206303
#3 -26.245902
#4 -55.206303
# ...
#7038 -37.343617
#7039 -8.695856
#7040 -47.472727
#7041 -53.432670
#7042 -10.063483
#Length: 7043, dtype: float64
- 组内归一化特征
所谓组内归一化特征，指的是用tenure减去MonthlyCharges_tenure_mean，再除以MonthlyCharges_tenure_std，其计算过程非常类似于归一化过程，即某列数据减去该列的均值再除以该列的标准差，这也是组内归一化名称的由来。具体计算过程如下：
(df['tenure'] - df['MonthlyCharges_tenure_mean']) / (np.sqrt(df['MonthlyCharges_tenure_var']) + 1e-5)
#0 -2.002322
#1 -1.210630
#2 -2.192403
#3 -0.856826
#4 -2.192403
# ...
#7038 -1.317354
#7039 -0.272113
#7040 -1.741320
#7041 -2.026832
#7042 -0.339537
#Length: 7043, dtype: float64
不难看出这些衍生过程仍然还是主要用到四则运算衍生方法，其计算过程并不复杂，而在实际操作过程中需要注意的是，往往需要同时带入基础的分组汇总衍生的特征和上述二阶衍生特征，才能起到更好的效果。
5.2 分组汇总特征彼此交叉衍生
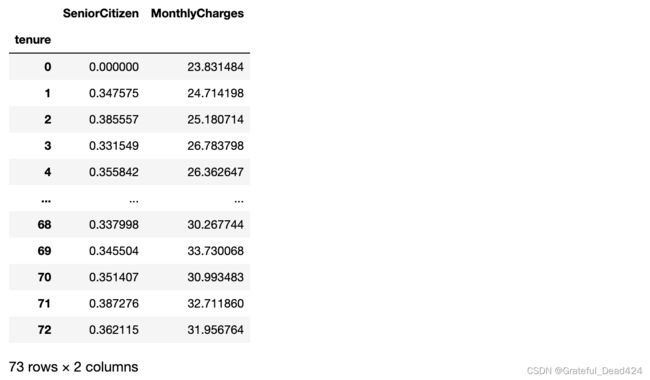
另外一类常用的二阶衍生特征，就是一系列基于分组汇总统计后的信息再次进行交叉衍生得到的新特征。这类特征往往具有较强的统计背景，能够更好的衡量原始特征的基本分布情况，还是在上述数据集中，以tenure作为分组依据，对月均消费金额进行分组汇总统计后，我们可以围绕这些统计指标进行二阶衍生：
col_num = ['MonthlyCharges']
df, col = Binary_Group_Statistics(keyCol, features, col_num)
df.head(5)
- Gap特征
Gap特征通过分组汇总后的上四分位数-下四分位数计算得出。在此前使用groupby进行分组统计的过程中我们并未使用分位数作为统计指标，具体分组分位数的计算过程需要借助，然后再带入groupby的过程：
当然，相同的计算过程也可应用于此前数据集中MonthlyCharges在不同tenure取值下的计算：
aggs = {'MonthlyCharges': [q1, q2]}
features_temp = features.groupby('tenure').agg(aggs).reset_index()
features_temp
features_temp.columns = ['tenure', 'MonthlyCharges_tenure_q1', 'MonthlyCharges_tenure_q2']
features_temp
features_temp['MonthlyCharges_tenure_q2-q1'] = features_temp['MonthlyCharges_tenure_q2'] - features_temp['MonthlyCharges_tenure_q1']
features_temp
- 数据倾斜
此外，我们还可以通过中位数和均值的比较来计算组内的数据倾斜情况：当均值大于中位数时，数据呈现正倾斜，均值小于中位数时，数据正弦负倾斜。当然衡量倾斜的方法有两种，其一是计算差值，其二则是计算比值：
col_num = ['MonthlyCharges']
df, col = Binary_Group_Statistics(keyCol, features, col_num)
df
df['MonthlyCharges_tenure_mean'] - df['MonthlyCharges_tenure_median']
#0 0.735808
#1 -4.305385
#2 -3.868697
#3 -9.754098
#4 -3.868697
# ...
#7038 1.943617
#7039 -8.379144
#7040 -2.777273
#7041 0.457670
#7042 -4.486517
#Length: 7043, dtype: float64
df['MonthlyCharges_tenure_mean'] / (df['MonthlyCharges_tenure_median'] + 1e-5)
#0 1.014790
#1 0.941780
#2 0.936656
#3 0.879579
#4 0.936656
# ...
#7038 1.032721
#7039 0.905931
#7040 0.954657
#7041 1.008033
#7042 0.944301
#Length: 7043, dtype: float64
- 变异系数
变异系数是通过分组统计的标准差除以均值，变异系数计算的是离中趋势，变异系数越大、说明数据离散程度越高，相关计算过程如下：
np.sqrt(df['MonthlyCharges_tenure_var']) / (df['MonthlyCharges_tenure_mean'] + 1e-10)
#0 0.489528
#1 0.422761
#2 0.440174
#3 0.429941
#4 0.440174
# ...
#7038 0.462109
#7039 0.396015
#7040 0.466243
#7041 0.459018
#7042 0.389659
#Length: 7043, dtype: float64
5.3 二阶特征衍生方法汇总
接下来我们通过一个函数封装上述所有常用的二阶衍生方法，同时，需要注意的是，该函数和此前定义的分组统计特征衍生函数彼此独立，进而方便在调用过程中可以针对不同的特征来进行不同阶数的衍生，当然也间接避免了重复讨论关于不同类别变量的不同统计指标的问题，唯一需要注意的是如果相同的特征同时带入一阶组内统计衍生和二阶衍生，则可能创造相同的特征，此时就需要在合并阶段进行列的去重处理。
def Group_Statistics_Extension(colNames, keyCol, features):
"""
双变量分组统计二阶特征衍生函数
:param colNames: 参与衍生的特征
:param keyCol: 分组参考的关键变量
:param features: 原始数据集
:return：交叉衍生后的新特征和新列名称
"""
# 定义四分位计算函数
def q1(x):
"""
下四分位数
"""
return x.quantile(0.25)
def q2(x):
"""
上四分位数
"""
return x.quantile(0.75)
# 一阶特征衍生
# 先定义用于生成列名称的aggs
aggs = {}
for col in colNames:
aggs[col] = ['mean', 'var', 'median', 'q1', 'q2']
cols = [keyCol]
for key in aggs.keys():
cols.extend([key+'_'+keyCol+'_'+stat for stat in aggs[key]])
# 再定义用于进行分组汇总的aggs
aggs = {}
for col in colNames:
aggs[col] = ['mean', 'var', 'median', q1, q2]
features_new = features[colNames+[keyCol]].groupby(keyCol).agg(aggs).reset_index()
features_new.columns = cols
features_new = pd.merge(features[keyCol], features_new, how='left',on=keyCol)
features_new.loc[:, ~features_new.columns.duplicated()]
colNames_new = cols
colNames_new.remove(keyCol)
# 二阶特征衍生
# 流量平滑特征
for col_temp in colNames:
col = col_temp+'_'+keyCol+'_'+'mean'
features_new[col_temp+'_dive1_'+col] = features_new[keyCol] / (features_new[col] + 1e-5)
colNames_new.append(col_temp+'_dive1_'+col)
col = col_temp+'_'+keyCol+'_'+'median'
features_new[col_temp+'_dive2_'+col] = features_new[keyCol] / (features_new[col] + 1e-5)
colNames_new.append(col_temp+'_dive2_'+col)
# 黄金组合特征
for col_temp in colNames:
col = col_temp+'_'+keyCol+'_'+'mean'
features_new[col_temp+'_minus1_'+col] = features_new[keyCol] - features_new[col]
colNames_new.append(col_temp+'_minus1_'+col)
col = col_temp+'_'+keyCol+'_'+'median'
features_new[col_temp+'_minus2_'+col] = features_new[keyCol] - features_new[col]
colNames_new.append(col_temp+'_minus2_'+col)
# 组内归一化特征
for col_temp in colNames:
col_mean = col_temp+'_'+keyCol+'_'+'mean'
col_var = col_temp+'_'+keyCol+'_'+'var'
features_new[col_temp+'_norm_'+keyCol] = (features_new[keyCol] - features_new[col_mean]) / (np.sqrt(features_new[col_var]) + 1e-5)
colNames_new.append(col_temp+'_norm_'+keyCol)
# Gap特征
for col_temp in colNames:
col_q1 = col_temp+'_'+keyCol+'_'+'q1'
col_q2 = col_temp+'_'+keyCol+'_'+'q2'
features_new[col_temp+'_gap_'+keyCol] = features_new[col_q2] - features_new[col_q1]
colNames_new.append(col_temp+'_gap_'+keyCol)
# 数据倾斜特征
for col_temp in colNames:
col_mean = col_temp+'_'+keyCol+'_'+'mean'
col_median = col_temp+'_'+keyCol+'_'+'median'
features_new[col_temp+'_mag1_'+keyCol] = features_new[col_median] - features_new[col_mean]
colNames_new.append(col_temp+'_mag1_'+keyCol)
features_new[col_temp+'_mag2_'+keyCol] = features_new[col_median] / (features_new[col_mean] + 1e-5)
colNames_new.append(col_temp+'_mag2_'+keyCol)
# 变异系数
for col_temp in colNames:
col_mean = col_temp+'_'+keyCol+'_'+'mean'
col_var = col_temp+'_'+keyCol+'_'+'var'
features_new[col_temp+'_cv_'+keyCol] = np.sqrt(features_new[col_var]) / (features_new[col_mean] + 1e-5)
colNames_new.append(col_temp+'_cv_'+keyCol)
features_new.drop([keyCol], axis=1, inplace=True)
return features_new, colNames_new
接下来测试函数效果：
keyCol = 'tenure'
colNames = ['MonthlyCharges', 'SeniorCitizen'] #一个连续变量，一个离散变量
features_new, colNames_new = Group_Statistics_Extension(colNames, keyCol, features)
features_new.head(5)
colNames_new
#['MonthlyCharges_tenure_mean',
# 'MonthlyCharges_tenure_var',
# 'MonthlyCharges_tenure_median',
# 'MonthlyCharges_tenure_q1',
# 'MonthlyCharges_tenure_q2',
# 'SeniorCitizen_tenure_mean',
# 'SeniorCitizen_tenure_var',
# 'SeniorCitizen_tenure_median',
# 'SeniorCitizen_tenure_q1',
# 'SeniorCitizen_tenure_q2',
# 'MonthlyCharges_dive1_MonthlyCharges_tenure_mean', # 流量平滑特征
# 'MonthlyCharges_dive2_MonthlyCharges_tenure_median',
# 'SeniorCitizen_dive1_SeniorCitizen_tenure_mean',
# 'SeniorCitizen_dive2_SeniorCitizen_tenure_median',
# 'MonthlyCharges_minus1_MonthlyCharges_tenure_mean', #黄金组合
# 'MonthlyCharges_minus2_MonthlyCharges_tenure_median',
# 'SeniorCitizen_minus1_SeniorCitizen_tenure_mean',
# 'SeniorCitizen_minus2_SeniorCitizen_tenure_median',
# 'MonthlyCharges_norm_tenure', # 组内归一化特征
# 'SeniorCitizen_norm_tenure',
# 'MonthlyCharges_gap_tenure', #gap
# 'SeniorCitizen_gap_tenure',
# 'MonthlyCharges_mag1_tenure', #数据倾斜
# 'MonthlyCharges_mag2_tenure',
# 'SeniorCitizen_mag1_tenure',
# 'SeniorCitizen_mag2_tenure',
# 'MonthlyCharges_cv_tenure', #变异系数
# 'SeniorCitizen_cv_tenure']
当然，至此我就完整讨论了关于双变量的组合衍生方法，接下来我们将进一步讨论多变量特征衍生方法。
三、多变量特征衍生方法
接下来，我们进一步介绍多变量衍生方法，不同于双变量衍生，多变量衍生由于一些原因（稍后会解释），导致其实际应用场景并不是很多，因此本部分内容以方法介绍为主，并针对重要的方法进行代码实现方面的介绍。
相比双变量衍生，多变量衍生并没有“额外的方法”，只是将双变量衍生的方法应用到多个变量上，从而实现多变量协同衍生。例如，当我们同时针对多个列进行加合运算，就相当于是多个特征的四则运算衍生（例如此前进行购买服务项的求和运算），该过程可以通过下述示例说明：
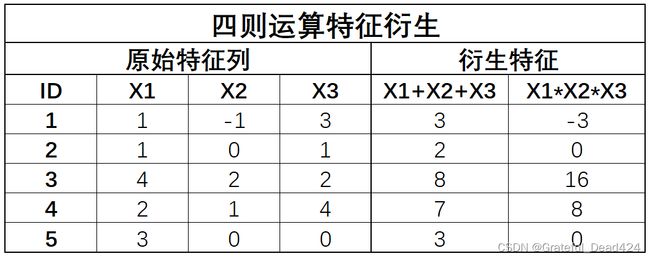
和双变量四则运算过程相同，在数据保存为DataFrame格式情况下，我们直接提取列进行四则运算即可。同样，多变量四则运算特征衍生的主要使用场景有两个，其一是需要补充一些特定业务字段时（例如统计每位用户购买服务项目总数），其二则是需要进行衍生字段的二阶段衍生时。
1.多变量的交叉组合特征衍生
- 原理介绍
接下来进一步讨论多变量的交叉组合特征衍生。同样，所谓多变量的交叉组合，就是将多个特征的不同取值水平进行组合，基本过程如下所示：
该过程并不复杂，但需要注意的是，伴随着交叉组合特征数量的增加、以及每个特征取值水平增加，衍生出来的特征数量将呈指数级上涨趋势，例如3个包含两个分类水平的离散变量进行交叉组合时，将衍生出 2 3 = 8 2^3=8 23=8个特征，而如果是10个包含三个分类水平的离散变量进行交叉组合，则将衍生出 3 10 = 59049 3^{10}=59049 310=59049个特征。当然，特征数量的多并没有太大影响，但如果同时特征矩阵过于稀疏（有较多零值），则表示相同规模数据情况下包含了较少信息，而这也将极大程度影响后续建模过程。
通过上述极简示例不难看出，通过交叉组合衍生出来的新特征矩阵是极度稀疏的（即0值占绝大多数），并且不难发现，每一行在衍生的特征矩阵中其实只有一个值是1，其余值都是0（只有组合出了一种取值）。可以证明，在m个n分类特征的交叉组合过程中，假设总共有k条数据，则0值的占比为：
n m ∗ k − k n m ∗ k = 1 − 1 n m \frac{n^m*k-k}{n^m*k}=1-\frac{1}{n^m} nm∗knm∗k−k=1−nm1即如果是3个2分类水平的特征进行交叉组合衍生，则新的特征矩阵中0值占比为 1 − 1 8 = 7 8 = 87.5 1-\frac{1}{8}=\frac{7}{8}=87.5 1−81=87=87.5%；而如果是10个三分类变量进行交叉组合衍生，则新特征矩阵中0值占比为 1 − 1 3 10 = 99.99831 1-\frac{1}{3^{10}}=99.99831 1−3101=99.99831%。尽管后续我们将介绍在海量特征中筛选有效特征的方法，但是在如此稀疏的矩阵中提取信息仍然还是一件非常困难的事情，因此往往我们并不会带入过多的特征进行交叉组合特征衍生。一般来说，如果有多个特征要进行交叉组合衍生，我们往往优先考虑两两组合进行交叉组合衍生，只有在人工判断是极为重要的特征情况下，才会考虑对其进行三个甚至更多的特征进行交叉组合衍生。
- 代码实现
多变量交叉组合具体的实现过程则与双变量交叉组合过程类似，同样我们以’SeniorCitizen’、‘Partner’、'Dependents’三个变量的交叉组合过程为例进行说明：
colNames = ['SeniorCitizen', 'Partner', 'Dependents']
# 单独提取目标字段的数据集
features_temp = features[colNames]
features_temp
接下来将这三列先“合并”成一列，该列名称为：
colNames_new = colNames[0] + '&' + colNames[1] + '&' + colNames[2]
colNames_new
#'SeniorCitizen&Partner&Dependents'
当然也可以通过join方法直接生成：
'&'.join(colNames)
#'SeniorCitizen&Partner&Dependents'
具体列数据为：
features_new = features['SeniorCitizen'].astype('str') + '&' + features['Partner'].astype('str') + '&' + features['Dependents'].astype('str')
features_new = pd.DataFrame(features_new)
features_new.columns = [colNames_new]
features_new.head(5)
当然，为了考虑到更为普适的情况，为了确保输入任意多个特征时都能完成上述过程，我们需要通过循环来执行：
colNames
#['SeniorCitizen', 'Partner', 'Dependents']
colNames[0]
#'SeniorCitizen'
colNames_new = '&'.join([str(i) for i in colNames])
features_new = features[colNames[0]].astype('str')
for col in colNames[1:]:
features_new = features_new + '&' + features[col].astype('str')
colNames_new
#'SeniorCitizen&Partner&Dependents'
features_new = pd.DataFrame(features_new)
features_new.columns = [colNames_new]
features_new
然后执行one-hot过程：
enc = preprocessing.OneHotEncoder()
enc.fit_transform(features_new)
#<7043x8 sparse matrix of type ''
# with 7043 stored elements in Compressed Sparse Row format>
colNames_new
#'SeniorCitizen&Partner&Dependents'
# 借助此前定义的列名称提取器进行列名称提取
cate_colName(enc, [colNames_new], drop=None)
#['SeniorCitizen&Partner&Dependents_0&No&No',
# 'SeniorCitizen&Partner&Dependents_0&No&Yes',
# 'SeniorCitizen&Partner&Dependents_0&Yes&No',
# 'SeniorCitizen&Partner&Dependents_0&Yes&Yes',
# 'SeniorCitizen&Partner&Dependents_1&No&No',
# 'SeniorCitizen&Partner&Dependents_1&No&Yes',
# 'SeniorCitizen&Partner&Dependents_1&Yes&No',
# 'SeniorCitizen&Partner&Dependents_1&Yes&Yes']
features_new_af = pd.DataFrame(enc.fit_transform(features_new).toarray(),
columns = cate_colName(enc, [colNames_new], drop=None))
features_new_af
features_new_af.shape
#(7043, 8)
接下来，考虑将上述过程封装为一个函数：
def Multi_Cross_Combination(colNames, features, OneHot=True):
"""
多变量组合交叉衍生
:param colNames: 参与交叉衍生的列名称
:param features: 原始数据集
:param OneHot: 是否进行独热编码
:return：交叉衍生后的新特征和新列名称
"""
# 创建组合特征
colNames_new = '&'.join([str(i) for i in colNames])
features_new = features[colNames[0]].astype('str')
for col in colNames[1:]:
features_new = features_new + '&' + features[col].astype('str')
# 将组合特征转化为DataFrame
features_new = pd.DataFrame(features_new, columns=[colNames_new])
# 对新的特征列进行独热编码
if OneHot == True:
enc = preprocessing.OneHotEncoder()
enc.fit_transform(features_new)
colNames_new = cate_colName(enc, [colNames_new], drop=None)
features_new = pd.DataFrame(enc.fit_transform(features_new).toarray(), columns=colNames_new)
return features_new, colNames_new
features_new, colNames_new = Multi_Cross_Combination(colNames, features)
features_new.head(5)
features_new.shape
#(7043, 8)
对比原始数据验证衍生过程是否正确：
features.head(5)
colNames_new
#['SeniorCitizen&Partner&Dependents_0&No&No',
# 'SeniorCitizen&Partner&Dependents_0&No&Yes',
# 'SeniorCitizen&Partner&Dependents_0&Yes&No',
# 'SeniorCitizen&Partner&Dependents_0&Yes&Yes',
# 'SeniorCitizen&Partner&Dependents_1&No&No',
# 'SeniorCitizen&Partner&Dependents_1&No&Yes',
# 'SeniorCitizen&Partner&Dependents_1&Yes&No',
# 'SeniorCitizen&Partner&Dependents_1&Yes&Yes']
至此我们就完成了多变量交叉特征衍生的全部过程。
2.多变量的分组统计特征衍生
- 方法介绍
接下来，进一步考虑多变量分组特征衍生的方法。在双变量分组特征衍生时，我们是选择某个特征为KeyCol（关键特征），然后以KeyCol的不同取值为作为分组依据，计算其他特征的统计量。而在多变量分组特征衍生的过程中，我们将考虑采用不同离散变量的交叉组合后的取值分组依据，再进行分组统计量的计算。在双变量分组统计汇总下，基本计算过程如下：
而多变量分组统计汇总基本过程如下：
此处是以tenure和SeniorCitizen交叉组合后的结果作为分组依据，对Monthly Charges进行分组汇总。除了分组的依据发生了变化外，分组统计过程和此前介绍的双变量分组统计特征衍生过程并没有任何差异。当然，从直观的结果上来看，多变量分组统计特征衍生能够更细粒度的呈现数据集信息，例如在以tenure作为分组依据统计Monthly Charges时相当于计算不同入网时间用户的平均月消费金额（以mean为例），而如果是以tenure与SeniorCitizen交叉组合结果作为分组依据统计Monthly Charges时，则相当于是计算不同入网时间、不同年龄段用户的平均消费金额，而往往更细粒度的信息展示就能够帮助模型达到更好的效果，因此，有限范围内的多变量分组统计特征衍生，是能达到更好的效果的。但同时需要注意的是，这种“细粒度”的呈现并不是越细粒度越好，我们知道，参与分组的交叉特征越多、分组也就越多，而在相同数据集下，分组越多、每一组的组内样本数量就越少，而在进行组内统计量计算时，如果组内样本数量太少，统计量往往就不具备代表性了，例如上述极简示例中ID为1的样本，在tenure和SeniorCitizen交叉分组后该样本所属分组只有一条样本，后续计算的统计量也没有任何“统计”方面的价值了。因此，多变量交叉分组也并不是越多变量越细粒度越好。一般来说，对于人工判断极重要的特征，可以考虑两个或三个特征进行交叉组合后分组。
- 代码实现
和双变量的分组统计类似，多变量分组统计也可以借助group过程来实现，首先简单回顾双变量的分组统计过程，然后在此基础上进一步考虑如何实现多变量的分组统计：
numeric_cols
#['tenure', 'MonthlyCharges', 'TotalCharges']
# 提取目标字段
colNames = ['tenure', 'SeniorCitizen', 'MonthlyCharges', 'TotalCharges']
# 单独提取目标字段的数据集
features_temp = features[colNames]
features_temp
# 在不同tenure取值下计算其他变量分组均值的结果
features_temp.groupby('tenure').mean()
# 使用agg方法同时统计多个统计指标
# 分组汇总字段
colNames_sub = ['SeniorCitizen', 'MonthlyCharges', 'TotalCharges']
# 创建空字典
aggs = {}
# 字段汇总统计量设置
for col in colNames_sub:
aggs[col] = ['mean', 'min', 'max']
aggs
#{'SeniorCitizen': ['mean', 'min', 'max'],
# 'MonthlyCharges': ['mean', 'min', 'max'],
# 'TotalCharges': ['mean', 'min', 'max']}
features_temp.groupby('tenure').agg(aggs).reset_index().head(5)
如果我们在groupby方法的参数中输入包含多个列的列名称的列表，则可以实现多列的交叉组合聚合：
features_temp.groupby(['tenure', 'SeniorCitizen']).mean().head(5)
当然，我们也可以配合agg过程，实现多统计量的多变量交叉聚合计算：
# 分组汇总字段
colNames_sub = ['MonthlyCharges', 'TotalCharges']
# 创建空字典
aggs = {}
# 字段汇总统计量设置
for col in colNames_sub:
aggs[col] = ['mean', 'min', 'max']
aggs
#{'MonthlyCharges': ['mean', 'min', 'max'],
# 'TotalCharges': ['mean', 'min', 'max']}
keycol = ['tenure', 'SeniorCitizen']
features_temp.groupby(keycol).agg(aggs).reset_index()
接下来生成列名称：
# 交叉组合列
keycol
#['tenure', 'SeniorCitizen']
# 创建包含交叉组合列及所有组合列名称组合的列表
cols = keycol.copy()
col_temp = cols[0]
for i in keycol[1: ]:
col_temp = col_temp + '&' + i
col_temp, cols
#('tenure&SeniorCitizen', ['tenure', 'SeniorCitizen'])
aggs.keys()
#dict_keys(['MonthlyCharges', 'TotalCharges'])
# 创建衍生列的列名称
for key in aggs.keys():
cols.extend([key+'_'+col_temp+'_'+stat for stat in aggs[key]])
cols
#['tenure',
# 'SeniorCitizen',
# 'MonthlyCharges_tenure&SeniorCitizen_mean',
# 'MonthlyCharges_tenure&SeniorCitizen_min',
# 'MonthlyCharges_tenure&SeniorCitizen_max',
# 'TotalCharges_tenure&SeniorCitizen_mean',
# 'TotalCharges_tenure&SeniorCitizen_min',
# 'TotalCharges_tenure&SeniorCitizen_max']
至此，我们即可完整创建新的特征矩阵：
features_new = features_temp.groupby(keycol).agg(aggs).reset_index()
features_new.columns = cols
features_new
接下来需要进一步考虑将衍生的特征矩阵拼接到原数据集上。这里需要注意的是，拼接过程中的主键其实是tenure和SeniorCitizen交叉组合的结果，所以这里我们需要现在原始数据集上创建一个tenure和SeniorCitizen交叉组合特征，然后再进行拼接，这里需要巧妙的借助此前定义的交叉组合函数来实现该过程：
keycol
#['tenure', 'SeniorCitizen']
# 原数据集进行关键列的交叉组合
features_key1, col1 = Multi_Cross_Combination(keycol, features, OneHot=False)
col1
#'tenure&SeniorCitizen'
list(features.columns)
#['gender',
# 'SeniorCitizen',
# 'Partner',
# 'Dependents',
# 'tenure',
# 'PhoneService',
# 'MultipleLines',
# 'InternetService',
# 'OnlineSecurity',
# 'OnlineBackup',
# 'DeviceProtection',
# 'TechSupport',
# 'StreamingTV',
# 'StreamingMovies',
# 'Contract',
# 'PaperlessBilling',
# 'PaymentMethod',
# 'MonthlyCharges',
# 'TotalCharges']
# 原数据集拼接时的主键
features_key1
pd.concat
# 新特征矩阵进行交叉组合
features_key2, col2 = Multi_Cross_Combination(keycol, features_new, OneHot=False)
features_key2
接下来进行数据集的拼接：
features_new_af = pd.concat([features_key2, features_new], axis=1)
features_new_af
features_new_m = pd.merge(features_key1, features_new_af, how='left',on='tenure&SeniorCitizen')
features_new_m
提取新特征的特征矩阵：
features_new_m.iloc[:, len(keycol)+1:] # +1是因为有一列交叉合成列
至此，我们即完成了多变量分组汇总统计特征衍生的全过程。接下来我们将上述过程封装为一个函数，同样，该函数是在双变量分组汇总函数基础上进行的修改：
def Multi_Group_Statistics(keyCol,
features,
col_num=None,
col_cat=None,
num_stat=['mean', 'var', 'max', 'min', 'skew', 'median'],
cat_stat=['mean', 'var', 'max', 'min', 'median', 'count', 'nunique'],
quant=True):
"""
多变量分组统计特征衍生函数
:param keyCol: 分组参考的关键变量
:param features: 原始数据集
:param col_num: 参与衍生的连续型变量
:param col_cat: 参与衍生的离散型变量
:param num_stat: 连续变量分组统计量
:param cat_num: 离散变量分组统计量
:param quant: 是否计算分位数
:return：交叉衍生后的新特征和新特征的名称
"""
# 生成原数据合并的主键
features_key1, col1 = Multi_Cross_Combination(keyCol, features, OneHot=False)
# 当输入的特征有连续型特征时
if col_num != None:
aggs_num = {}
colNames = col_num
# 创建agg方法所需字典
for col in col_num:
aggs_num[col] = num_stat
# 创建衍生特征名称列表
cols_num = keyCol.copy()
for key in aggs_num.keys():
cols_num.extend([key+'_'+col1+'_'+stat for stat in aggs_num[key]])
# 创建衍生特征df
features_num_new = features[col_num+keyCol].groupby(keyCol).agg(aggs_num).reset_index()
features_num_new.columns = cols_num
# 生成主键
features_key2, col2 = Multi_Cross_Combination(keyCol, features_num_new, OneHot=False)
# 创建包含合并主键的数据集
features_num_new = pd.concat([features_key2, features_num_new], axis=1)
# 当输入的特征有连续型也有离散型特征时
if col_cat != None:
aggs_cat = {}
colNames = col_num + col_cat
# 创建agg方法所需字典
for col in col_cat:
aggs_cat[col] = cat_stat
# 创建衍生特征名称列表
cols_cat = keyCol.copy()
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+col1+'_'+stat for stat in aggs_cat[key]])
# 创建衍生特征df
features_cat_new = features[col_cat+keyCol].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
# 生成主键
features_key3, col3 = Multi_Cross_Combination(keyCol, features_cat_new, OneHot=False)
# 创建包含合并主键的数据集
features_cat_new = pd.concat([features_key3, features_cat_new], axis=1)
# 合并连续变量衍生结果与离散变量衍生结果
# 合并新的特征矩阵
df_temp = pd.concat([features_num_new, features_cat_new], axis=1)
df_temp = df_temp.loc[:, ~df_temp.columns.duplicated()]
# 将新的特征矩阵与原始数据集合并
features_new = pd.merge(features_key1, df_temp, how='left',on=col1)
# 当只有连续变量时
else:
# merge连续变量衍生结果与原始数据，然后删除重复列
features_new = pd.merge(features_key1, features_num_new, how='left',on=col1)
features_new = features_new.loc[:, ~features_new.columns.duplicated()]
# 当没有输入连续变量时
else:
# 但存在分类变量时，即只有分类变量时
if col_cat != None:
aggs_cat = {}
colNames = col_cat
for col in col_cat:
aggs_cat[col] = cat_stat
cols_cat = keyCol.copy()
for key in aggs_cat.keys():
cols_cat.extend([key+'_'+col1+'_'+stat for stat in aggs_cat[key]])
features_cat_new = features[col_cat+keyCol].groupby(keyCol).agg(aggs_cat).reset_index()
features_cat_new.columns = cols_cat
features_new = pd.merge(features_key1, features_cat_new, how='left',on=col1)
features_new = features_new.loc[:, ~features_new.columns.duplicated()]
if quant:
# 定义四分位计算函数
def q1(x):
"""
下四分位数
"""
return x.quantile(0.25)
def q2(x):
"""
上四分位数
"""
return x.quantile(0.75)
aggs = {}
for col in colNames:
aggs[col] = ['q1', 'q2']
cols = keyCol.copy()
for key in aggs.keys():
cols.extend([key+'_'+col1+'_'+stat for stat in aggs[key]])
aggs = {}
for col in colNames:
aggs[col] = [q1, q2]
features_temp = features[colNames+keyCol].groupby(keyCol).agg(aggs).reset_index()
features_temp.columns = cols
features_new.drop(keyCol, axis=1, inplace=True)
# 生成主键
features_key4, col4 = Multi_Cross_Combination(keyCol, features_temp, OneHot=False)
# 创建包含合并主键的数据集
features_temp = pd.concat([features_key4, features_temp], axis=1)
# 合并新特征矩阵
features_new = pd.merge(features_new, features_temp, how='left',on=col1)
features_new = features_new.loc[:, ~features_new.columns.duplicated()]
features_new.drop(keyCol+[col1], axis=1, inplace=True)
colNames_new = list(features_new.columns)
return features_new, colNames_new
然后，我们尝试同时带入连续型特征和离散型特征进行函数效果验证，此处我们以’tenure’、'SeniorCitizen’的交叉组合结果作为分组依据，‘MonthlyCharges’、'TotalCharges’作为连续变量进行统计，'Partner’作为离散变量进行统计，基本过程如下：
numeric_cols
#['tenure', 'MonthlyCharges', 'TotalCharges']
cols = ['tenure', 'SeniorCitizen', 'MonthlyCharges', 'TotalCharges' , 'Partner']
keyCol = ['tenure', 'SeniorCitizen']
col_num = ['MonthlyCharges', 'TotalCharges']
col_cat = ['Partner']
features_OE = features[cols]
features_OE
考虑到数据集中存在Object对象类型，在进行分组统计前需要对其进行自然数转化：
enc = preprocessing.OrdinalEncoder(dtype=int)
features_OE['Partner'] = enc.fit_transform(pd.DataFrame(features_OE['Partner']))
features_OE
然后即可带入函数进行验证：
features_new, colNames_new = Multi_Group_Statistics(keyCol, features_OE, col_num, col_cat)
features_new.head(5)
colNames_new
#['MonthlyCharges_tenure&SeniorCitizen_mean',
# 'MonthlyCharges_tenure&SeniorCitizen_var',
# 'MonthlyCharges_tenure&SeniorCitizen_max',
# 'MonthlyCharges_tenure&SeniorCitizen_min',
# 'MonthlyCharges_tenure&SeniorCitizen_skew',
# 'MonthlyCharges_tenure&SeniorCitizen_median',
# 'TotalCharges_tenure&SeniorCitizen_mean',
# 'TotalCharges_tenure&SeniorCitizen_var',
# 'TotalCharges_tenure&SeniorCitizen_max',
# 'TotalCharges_tenure&SeniorCitizen_min',
# 'TotalCharges_tenure&SeniorCitizen_skew',
# 'TotalCharges_tenure&SeniorCitizen_median',
# 'Partner_tenure&SeniorCitizen_mean',
# 'Partner_tenure&SeniorCitizen_var',
# 'Partner_tenure&SeniorCitizen_max',
# 'Partner_tenure&SeniorCitizen_min',
# 'Partner_tenure&SeniorCitizen_median',
# 'Partner_tenure&SeniorCitizen_count',
# 'Partner_tenure&SeniorCitizen_nunique',
# 'MonthlyCharges_tenure&SeniorCitizen_q1',
# 'MonthlyCharges_tenure&SeniorCitizen_q2',
# 'TotalCharges_tenure&SeniorCitizen_q1',
# 'TotalCharges_tenure&SeniorCitizen_q2',
# 'Partner_tenure&SeniorCitizen_q1',
# 'Partner_tenure&SeniorCitizen_q2']
能够看到函数能够完整执行多变量交叉组合分组统计。
3.多变量的多项式特征衍生
- 方法介绍
接下来进一步介绍多变量的多项式衍生，多变量的多项式衍生过程并不复杂，无非就是在多项式计算时带入更多特征进行计算，而在进行多项式计算时并无本质区别，都是进行幂运算和交叉项计算。首先回顾双变量二阶多项式衍生过程：
此时如果我们增加参与多项式计算的特征，则有如下多变量多项式衍生过程：
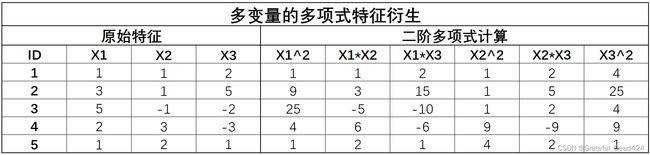
当然，对于二阶多项式衍生，多变量的计算过程其实等价于多个双变量组合衍生的结果，例如上述X1、X2、X3三个变量的二阶多项式衍生，其实就等价于X1和X2、X1和X3（或X2、X3）两组二阶多项式衍生后去重的结果，因此如果是二阶多项式衍生的话，多变量的交叉组合结果完全等价于多变量中两两变量的二阶多项式衍生结果。但如果是三阶甚至是更高阶的多项式衍生，结果就会有所不同：
不难发现，多变量的多项式衍生和多变量两两交叉多项式衍生的差异主要体现在多个变量的交叉项上，当然伴随着多项式阶数增加，多变量交叉项本身也会更多更复杂，二者差异也会更加明显。当然，多个特征的交叉组合乘积也同样会增加特征的表现，但同时也会增加伴随着多变量多项式衍生的变量数量增加以及阶数的增加，特征数量也会呈指数级增加趋势，并且衍生特征的取值也将变得非常不稳定，会伴随着阶数增加绝对值快速趋近于0或者一个非常大的数。因此，和此前的多变量特征衍生方法的使用场景类似，一般是针对人工判断的非常重要的特征可以考虑进行多变量的三阶甚至四阶多项式衍生。
- 代码实现
多变量的高阶多项式衍生也可以通过PolynomialFeatures快速实现：
from sklearn.preprocessing import PolynomialFeatures
df = pd.DataFrame({'X1':[1, 3, 5], 'X2':[1, 1, -1], 'X3':[2, 5, -2]})
df
PolynomialFeatures(degree=2, include_bias=False).fit_transform(df)
#array([[ 1., 1., 2., 1., 1., 2., 1., 2., 4.],
# [ 3., 1., 5., 9., 3., 15., 1., 5., 25.],
# [ 5., -1., -2., 25., -5., -10., 1., 2., 4.]])
和双变量的多项式特征衍生规律类似，多变量的多项式衍生特征的列排布顺序规律如下所示：
即首先是各特征的1次方（也就是原始特征本身），然后按照X1、X2、X3依次降序顺序进行组合。当然，如果是三次方多项式衍生，结果如下：
PolynomialFeatures(degree=3, include_bias=False).fit_transform(df)
#array([[ 1., 1., 2., 1., 1., 2., 1., 2., 4., 1., 1.,
# 2., 1., 2., 4., 1., 2., 4., 8.],
# [ 3., 1., 5., 9., 3., 15., 1., 5., 25., 27., 9.,
# 45., 3., 15., 75., 1., 5., 25., 125.],
# [ 5., -1., -2., 25., -5., -10., 1., 2., 4., 125., -25.,
# -50., 5., 10., 20., -1., -2., -4., -8.]])
上述结果包含了二阶和三阶多项式衍生结果，此处单独提取三阶多项式衍生结果：
PolynomialFeatures(degree=3, include_bias=False).fit_transform(df)[:, 9:]
#array([[ 1., 1., 2., 1., 2., 4., 1., 2., 4., 8.],
# [ 27., 9., 45., 3., 15., 75., 1., 5., 25., 125.],
# [125., -25., -50., 5., 10., 20., -1., -2., -4., -8.]])
从该结果中能看出三阶衍生特征排布规律，仍然是按照X1、X2、X3依次降序顺序进行组合排列，衍生列的顺序为： X 1 3 ∗ X 2 0 ∗ X 3 0 X_1^3*X_2^0*X_3^0 X13∗X20∗X30、 X 1 2 ∗ X 2 1 ∗ X 3 0 X_1^2*X_2^1*X_3^0 X12∗X21∗X30、 X 1 2 ∗ X 2 0 ∗ X 3 1 X_1^2*X_2^0*X_3^1 X12∗X20∗X31、 X 1 1 ∗ X 2 2 ∗ X 3 0 X_1^1*X_2^2*X_3^0 X11∗X22∗X30、 X 1 1 ∗ X 2 1 ∗ X 3 1 X_1^1*X_2^1*X_3^1 X11∗X21∗X31、 X 1 1 ∗ X 2 0 ∗ X 3 2 X_1^1*X_2^0*X_3^2 X11∗X20∗X32、 X 1 0 ∗ X 2 3 ∗ X 3 0 X_1^0*X_2^3*X_3^0 X10∗X23∗X30、 X 1 0 ∗ X 2 2 ∗ X 3 1 X_1^0*X_2^2*X_3^1 X10∗X22∗X31、 X 1 0 ∗ X 2 1 ∗ X 3 2 X_1^0*X_2^1*X_3^2 X10∗X21∗X32、 X 1 0 ∗ X 2 0 ∗ X 3 3 X_1^0*X_2^0*X_3^3 X10∗X20∗X33:
尽管看起来列名称的规律非常明显，但要通过代码实现却并不简单，首先我们采用下述格式进行更加简洁的列名称的展示：
# X1的三次方项
'X1&X2&X3_(3, 0, 0)'
#'X1&X2&X3_(3, 0, 0)'
# X1的二次方*X2的一次方项
'X1&X2&X3_(2, 1, 0)'
#'X1&X2&X3_(2, 1, 0)'
此处X1&X2&X3项的名称可以通过join方法生成:
'&'.join(cols)
#'X1&X2&X3'
接下来就是创建代表阶数的数值项。首先我们知道，最终目标是创建如下顺序的数值列表：
tar = [[3, 0, 0],
[2, 1, 0],
[2, 0, 1],
[1, 2, 0],
[1, 1, 1],
[1, 0, 2],
[0, 3, 0],
[0, 2, 1],
[0, 1, 2],
[0, 0, 3]]
tar
#[[3, 0, 0],
# [2, 1, 0],
# [2, 0, 1],
# [1, 2, 0],
# [1, 1, 1],
# [1, 0, 2],
# [0, 3, 0],
# [0, 2, 1],
# [0, 1, 2],
# [0, 0, 3]]
我们可以通过一些类似递归的方法来创建该数组，当然也可以采用一种更加巧妙的方法、通过笛卡尔积的计算过程来进行创建。笛卡尔积的计算函数在itertools库内，该库是python自带的库，直接通过下述方法导入即可：
from itertools import product
其中product函数就是笛卡尔积计算函数。我们先通过一个简单示例看下笛卡尔积的计算过程：
list(product([1, 2], ['a', 'b']))
#[(1, 'a'), (1, 'b'), (2, 'a'), (2, 'b')]
不难发现，笛卡尔积的计算过程就是不同对象的不同位置元素依次排列组合后的结果。这里我们尝试通过笛卡尔积创建这样的一个序列的集合，该序列包含三个元素，每个元素都在[0,3]范围内取值，并且按照前后顺序进行降序排列，即类似如下情况：
[ [ 3 , 3 , 3 ] , [ 3 , 3 , 2 ] , [ 3 , 3 , 1 ] , [ 3 , 3 , 0 ] , . . . [ 0 , 0 , 2 ] , [ 0 , 0 , 1 ] ] [[3, 3, 3], [3, 3, 2], [3, 3, 1], [3, 3, 0], ... [0, 0, 2], [0, 0, 1]] [[3,3,3],[3,3,2],[3,3,1],[3,3,0],...[0,0,2],[0,0,1]]
然后我们从该数组中挑选每个序列三个元素之和等于3的序列，这些序列构成的数组便是我们需要寻找的目标数组。我们可以通过如下代码完成该过程：
for x, y, z in product(range(3, -1, -1), range(3, -1, -1), range(3, -1, -1)):
print(x, y, z)
#3 3 3
#3 3 2
#3 3 1
#3 3 0
#3 2 3
#3 2 2
#3 2 1
#3 2 0
#3 1 3
#3 1 2
#3 1 1
#3 1 0
#3 0 3
#3 0 2
#3 0 1
#3 0 0
#2 3 3
#2 3 2
#2 3 1
#2 3 0
#...
#0 0 3
#0 0 2
#0 0 1
#0 0 0
尽管上述过程能够创建我们所需要的数组，但是需要注意的是，由于后续我们需要将该过程封装为一个函数，因此创建数组的关键参数：如每个序列每个元素的取值范围、多少元素参与笛卡尔积运算等，均不能在流程上“写死”。我们需要重写一个看起来略显复杂，但是更具有可拓展性的流程：
deg = 3
n = len(cols)
l = []
deg, n
#(3, 3)
a1 = range(3, -1, -1)
a1 = list(product(a1, range(3, -1, -1)))
a1[:5]
#[(3, 3), (3, 2), (3, 1), (3, 0), (2, 3)]
a1 = list(product(a1, range(3, -1, -1)))
a1[:5]
#[((3, 3), 3), ((3, 3), 2), ((3, 3), 1), ((3, 3), 0), ((3, 2), 3)]
接下来我们通过如下过程将带有元组的列表转化成包含元组元素的列表：
a2 = []
for i in a1:
i_temp = list(i[0])
i_temp.append(i[1])
a2.append(i_temp)
a2[:5]
#[[3, 3, 3], [3, 3, 2], [3, 3, 1], [3, 3, 0], [3, 2, 3]]
上述过程可以封装如下，其中n代表参与参与交叉组合的特征个数，同时也是控制外层循环次数的参数，deg代表多项式计算的最高阶数，同时也是控制数组中最大数的参数：
m = 1
a1 = range(deg, -1, -1)
a2 = []
while m < n:
a1 = list(product(a1, range(deg, -1, -1)))
if m > 1:
for i in a1:
i_temp = list(i[0])
i_temp.append(i[1])
a2.append(i_temp)
m += 1
a2[:5]
#[[3, 3, 3], [3, 3, 2], [3, 3, 1], [3, 3, 0], [3, 2, 3]]
接下来，我们需要在a2中提取出按行求和等于3的元素，为了便于统计运算，我们需要将a2转化为array：
a2 = np.array(a2)
# 按行求和
a2.sum(1)
#array([9, 8, 7, 6, 8, 7, 6, 5, 7, 6, 5, 4, 6, 5, 4, 3, 8, 7, 6, 5, 7, 6,
# 5, 4, 6, 5, 4, 3, 5, 4, 3, 2, 7, 6, 5, 4, 6, 5, 4, 3, 5, 4, 3, 2,
# 4, 3, 2, 1, 6, 5, 4, 3, 5, 4, 3, 2, 4, 3, 2, 1, 3, 2, 1, 0])
# 挑选和为3的行
a3 = a2[a2.sum(1) == 3]
a3
#array([[3, 0, 0],
# [2, 1, 0],
# [2, 0, 1],
# [1, 2, 0],
# [1, 1, 1],
# [1, 0, 2],
# [0, 3, 0],
# [0, 2, 1],
# [0, 1, 2],
# [0, 0, 3]])
而a3就是我们的目标数组：
tar
#[[3, 0, 0],
# [2, 1, 0],
# [2, 0, 1],
# [1, 2, 0],
# [1, 1, 1],
# [1, 0, 2],
# [0, 3, 0],
# [0, 2, 1],
# [0, 1, 2],
# [0, 0, 3]]
a3.tolist() == tar
#True
接下来，在a3的基础上，创建新的列名称，其中，每一个新特征的名称可以通过如下方式进行创建：
cols
#['X1', 'X2', 'X3']
''.join([str(i) for i in a3[0]])
#'300'
'&'.join(cols) + '_' + ''.join([str(i) for i in a3[0]])
#'X1&X2&X3_300'
然后我们可以通过循环来创建并保存所有新列的名称：
colNames = []
for i in a3:
colNames.append('&'.join(cols) + '_' + ''.join([str(i) for i in i]))
colNames
#['X1&X2&X3_300',
# 'X1&X2&X3_210',
# 'X1&X2&X3_201',
# 'X1&X2&X3_120',
# 'X1&X2&X3_111',
# 'X1&X2&X3_102',
# 'X1&X2&X3_030',
# 'X1&X2&X3_021',
# 'X1&X2&X3_012',
# 'X1&X2&X3_003']
df_p3 = PolynomialFeatures(degree=3, include_bias=False).fit_transform(df)[:, 9:]
df_p3
#array([[ 1., 1., 2., 1., 2., 4., 1., 2., 4., 8.],
# [ 27., 9., 45., 3., 15., 75., 1., 5., 25., 125.],
# [125., -25., -50., 5., 10., 20., -1., -2., -4., -8.]])
然后，我们将其合并为一个三阶多项式衍生的最终结果：
df_p3 = pd.DataFrame(df_p3, columns=colNames)
df_p3
当然，我们也可以验证二阶多项式衍生的结果：
deg = 2
n = len(cols)
l = []
deg, n
#(2, 3)
m = 1
a1 = range(deg, -1, -1)
a2 = []
while m < n:
a1 = list(product(a1, range(deg, -1, -1)))
if m > 1:
for i in a1:
i_temp = list(i[0])
i_temp.append(i[1])
a2.append(i_temp)
m += 1
a2 = np.array(a2)
# 挑选和为3的行
a3 = a2[a2.sum(1) == deg]
a3
#array([[2, 0, 0],
# [1, 1, 0],
# [1, 0, 1],
# [0, 2, 0],
# [0, 1, 1],
# [0, 0, 2]])
接下来，我们将上述过程封装为一个完整的函数:
def Muti_PolynomialFeatures(colNames, degree, features):
"""
连续变量多变量多项式衍生函数
:param colNames: 参与交叉衍生的列名称
:param degree: 多项式最高阶
:param features: 原始数据集
:return：交叉衍生后的新特征和新列名称
"""
# 创建空列表容器
colNames_new_l = []
# 计算带入多项式计算的特征数
n = len(colNames)
# 提取需要进行多项式衍生的特征
features = features[colNames]
# 进行多项式特征组合
array_new_temp = PolynomialFeatures(degree=degree, include_bias=False).fit_transform(features)
# 选取衍生的特征
array_new_temp = array_new_temp[:, n:]
# 创建列名称列表
deg = 2
while deg <= degree:
m = 1
a1 = range(deg, -1, -1)
a2 = []
while m < n:
a1 = list(product(a1, range(deg, -1, -1)))
if m > 1:
for i in a1:
i_temp = list(i[0])
i_temp.append(i[1])
a2.append(i_temp)
m += 1
a2 = np.array(a2)
a3 = a2[a2.sum(1) == deg]
for i in a3:
colNames_new_l.append('&'.join(colNames) + '_' + ''.join([str(i) for i in i]))
deg += 1
# 拼接新特征矩阵
features_new = pd.DataFrame(array_new_temp, columns=colNames_new_l)
colNames_new = colNames_new_l
return features_new, colNames_new
接下来，验证函数效果：
df[cols]
df
cols
#['X1', 'X2', 'X3']
features_new, colNames_new = Muti_PolynomialFeatures(cols, 4, df)
features_new
至此，我们即完成了多变量的多项式特征衍生的代码实现。
四、关键特征衍生策略
在大多数情况下，我们只需要合理使用上述双变量和多变量特征衍生方法，就能快速构建海量新特征，并且通过上述方法构建的特征池往往也都包含了绝大多数的潜在有效特征。当然，上述方法的具体使用经验还有待在后续案例中逐渐积累，但需要注意的是，对于某些“特殊”的特征，是无法通过上述自动化特征衍生方法进行更深入的有效信息挖掘的，在机器学习领域中，这些“特殊”的特征就是时序特征和文本特征，例如此前数据集中的tenure字段就属于时序字段，文本类型字段目前暂未遇到，留与后续内容进行介绍。
而对于时序特征，往往都包含更多更复杂的信息，例如tenure字段，截至目前我们只知道tenure字段代表用户入网时间，并且数值越大表示用户入网时间越早，并且tenure字段和标签呈现负相关，即入网时间越早的用户（tenure字段取值越大）越不容易流失：
# 剔除ID列
df3 = tcc.iloc[:,1:].copy()
# 将标签Yes/No转化为1/0
df3['Churn'].replace(to_replace='Yes', value=1, inplace=True)
df3['Churn'].replace(to_replace='No', value=0, inplace=True)
# 将其他所有分类变量转化为哑变量，连续变量保留不变
df_dummies = pd.get_dummies(df3)
# 绘制柱状图
sns.set()
plt.figure(figsize=(15,8), dpi=200)
df_dummies.corr()['Churn'].sort_values(ascending = False).plot(kind='bar')
但除此以外，是否还会有其他的“隐藏规律”呢？例如用户的流失是否会和季节相关、或者和每年的月份相关呢？很明显，若想围绕时序字段进一步深挖这些规律，仅仅凭借此前介绍的特征衍生方法是无法做到的。
为了更深入的挖掘时许字段的隐藏信息，我们需要补充一些专门用于围绕时序进行特征衍生和规律挖掘的方法。接下来我们将先以tenure字段为例来进行分析。
1.时序特征衍生方法
1.1 tenure时序字段分析
所谓的时序特征，其实就是指记录了时间的特征，例如交易发生时间、用户入网时间等，在Telco数据集中，tenure字段就是时序字段。而对于时序字段来说，也绝不仅仅是一串记录了事件发生时间的数字或者字符串这么简单，其背后往往可能隐藏着非常多极有价值的信息，例如在很多场景下数据集的标签都会具有季节性波动规律，对应到上述数据集就是用户流失很有可能与季节、月份相关。而要围绕这点进行分析，我们首先就需要将tenure数值型字段转化为年-月-季度的基本格式。
- 时间信息的更细粒度周期划分
假设tenure是以月为时间跨度进行的记录，则tenure的取值范围[0, 72]就表示过去6年（也就是72个月）的时间记录结果。并且我们知道，tenure取值越大代表的记录的时间越久远。假设tenure=0表示的是2020年1月，则tenure=1则代表2019年12月，则tenure=2代表2019年11月依此类推。那么据此，我们可以根据tenure字段衍生出更多的、用于呈现更细粒度时间信息的字段，即衍生出某个用户入网时间所属年、月、季度等，基本过程如下所示：
由于数据集解释中并未给出实际统计时间跨度，因此此处的2014-2020也仅作示例使用，若统计时间区间为其他时间跨度，也可参照该方法进行计算。
而实际代码实现过程也较为简单，只需要借助numpy的广播特性，围绕tenure列进行除法和取余计算即可。首先我们需要先将tenure字段进行倒序处理，即数值越大代表距离开始统计的时间越远，即tenure=0表示开始统计的第一个月、即2014年1月，而tenure=72则表示结束统计的最后一个月，即2020年1月：
features['tenure'].head()
#0 1
#1 34
#2 2
#3 45
#4 2
#Name: tenure, dtype: int64
(72 - features['tenure']).head()
#0 71
#1 38
#2 70
#3 27
#4 70
#Name: tenure, dtype: int64
在倒序处理后，我们通过取余的运算就能够算出用户入网所属月，此处我们先创建一个[0,72]的数组用于举例，然后再回归到原始数据集上进行计算：
a1 = np.arange(73)
a1
#array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
# 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
# 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
# 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
# 68, 69, 70, 71, 72])
a1 % 12
#array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 4,
# 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
# 10, 11, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2,
# 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 4, 5, 6, 7,
# 8, 9, 10, 11, 0])
# 计算所属月份
a1_month = a1 % 12 + 1
a1_month
#array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5,
# 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
# 11, 12, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3,
# 4, 5, 6, 7, 8, 9, 10, 11, 12, 1, 2, 3, 4, 5, 6, 7, 8,
# 9, 10, 11, 12, 1], dtype=int32)
这里需要注意，因为月份是从1-12进行排布，而任意一个数除以12的余数则是0到11，因此需要在余数基础上进一步加1。并且，在此结果基础上，进一步进行取整运算（相除之后的结果取下整数），即可算出每个月份所属季度：
# 计算所属季度
((a1_month-1) // 3) + 1
#array([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4,
# 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3,
# 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2,
# 3, 3, 3, 4, 4, 4, 1], dtype=int32)
a1_quarter = ((a1_month-1) // 3) + 1
a1_quarter
#array([1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4,
# 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3,
# 3, 4, 4, 4, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 1, 1, 1, 2, 2, 2,
# 3, 3, 3, 4, 4, 4, 1], dtype=int32)
然后我们再通过取整运算，则可以算出每位用户入网所属年：
(a1 // 12) + 2014
#array([2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014,
# 2014, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015,
# 2015, 2015, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016,
# 2016, 2016, 2016, 2017, 2017, 2017, 2017, 2017, 2017, 2017, 2017,
# 2017, 2017, 2017, 2017, 2018, 2018, 2018, 2018, 2018, 2018, 2018,
# 2018, 2018, 2018, 2018, 2018, 2019, 2019, 2019, 2019, 2019, 2019,
# 2019, 2019, 2019, 2019, 2019, 2019, 2020], dtype=int32)
a1_year = (a1 // 12) + 2014
a1_year
#array([2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014, 2014,
# 2014, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015, 2015,
# 2015, 2015, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016, 2016,
# 2016, 2016, 2016, 2017, 2017, 2017, 2017, 2017, 2017, 2017, 2017,
# 2017, 2017, 2017, 2017, 2018, 2018, 2018, 2018, 2018, 2018, 2018,
# 2018, 2018, 2018, 2018, 2018, 2019, 2019, 2019, 2019, 2019, 2019,
# 2019, 2019, 2019, 2019, 2019, 2019, 2020], dtype=int32)
当然，年份的转化也可以借助等频分箱完成（需要先把tenure=0进行单独提取）。
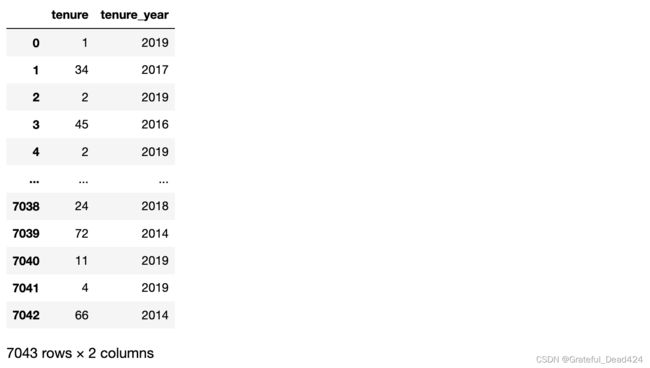
接下来，我们在原始数据集的tenure列上进行年、月、季度的特征衍生：
feature_seq = pd.DataFrame()
feature_seq['tenure'] = features['tenure']
# 年份衍生
feature_seq['tenure_year'] = ((72 - features['tenure']) // 12) + 2014
feature_seq.head()
# 月份衍生
feature_seq['tenure_month'] = (72 - features['tenure']) % 12 + 1
# 季度衍生
feature_seq['tenure_quarter'] = ((feature_seq['tenure_month']-1) // 3) + 1
feature_seq
至此，我们就根据tenure字段完成了更细粒度的时间划分。接下来我们就从这些更细粒度刻画时间的字段入手进行分析。
- 时间衍生字段分析
根据此前的分析我们知道，tenure和用户流失呈现明显的负相关，即tenure取值越大（越是老用户），用户流失的概率就越小，接下来我们进一步分析用户流失是否和入网年份、月份和季度有关：
feature_seq['Churn'] = labels
feature_seq
当然，我们可以首先简单尝试计算相关系数，这里需要注意的是，在未进行独热编码之前，相关系数的计算实际上会将拥有多个取值水平的分类变量视作连续变量来进行计算。例如quarter取值为[1,4]，则相关系数的计算过程是quarter取值越大、流失概率如何变化：
feature_seq.corr()
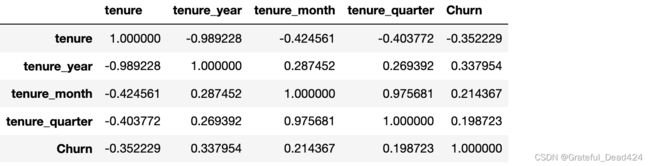
出于更严谨的角度考虑，我们还是需要将年、月、季度等字段进行独热编码，毕竟类似“所在季度越靠后（quarter取值越大）流失概率越大的规律可能并不能完整的表示季度与用户流失率之间的关系。
seq_new = ['tenure_year', 'tenure_month', 'tenure_quarter']
feature_seq_new = feature_seq[seq_new]
feature_seq_new
feature_seq_new.tenure_year=feature_seq_new.tenure_year.astype("str")
feature_seq_new.tenure_month=feature_seq_new.tenure_month.astype("str")
feature_seq_new.tenure_quarter=feature_seq_new.tenure_quarter.astype("str")
enc = preprocessing.OneHotEncoder()
enc.fit_transform(feature_seq_new)
seq_new
#['tenure_year', 'tenure_month', 'tenure_quarter']
# 借助此前定义的列名称提取器进行列名称提取
cate_colName(enc, seq_new, drop=None)
#['tenure_year_2014',
# 'tenure_year_2015',
# 'tenure_year_2016',
# 'tenure_year_2017',
# 'tenure_year_2018',
# 'tenure_year_2019',
# 'tenure_year_2020',
# 'tenure_month_1',
# 'tenure_month_10',
# 'tenure_month_11',
# 'tenure_month_12',
# 'tenure_month_2',
# 'tenure_month_3',
# 'tenure_month_4',
# 'tenure_month_5',
# 'tenure_month_6',
# 'tenure_month_7',
# 'tenure_month_8',
# 'tenure_month_9',
# 'tenure_quarter_1',
# 'tenure_quarter_2',
# 'tenure_quarter_3',
# 'tenure_quarter_4']
# 创建带有列名称的独热编码之后的df
features_seq_new = pd.DataFrame(enc.fit_transform(feature_seq_new).toarray(),
columns = cate_colName(enc, seq_new, drop=None))
features_seq_new
# 添加标签列
features_seq_new['Churn'] = labels
features_seq_new
接下来即可通过柱状图来观察用户不同入网时间与流失率之间的相关关系
sns.set()
plt.figure(figsize=(15,8), dpi=200)
features_seq_new.corr()['Churn'].sort_values(ascending = False).plot(kind='bar')
能够看出，2019年入网用户普遍流失率更大、而2014年入网用户普遍流失率更小，当然这个和tenure字段与标签的相关性表现出来的规律是一致的，即越是新入网的用户、流失概率越大，尽管该规律真实有效，但在实际使用过程中还是要注意区分场景，如果是针对既有用户（例如过去6年积累下来的所有用户）进行流失率预测，则入网时长就将是重要特征，但如果是要针对每个月入网的新用户进行流失率的实时预测，则入网年份可能就不是那么重要了，此时我们则需要更关注例如12月和第四季度入网用户普遍容易流失、而1月和第一季度入网用户流失率相对较低这类规律。
但不管怎样，我们都可以将这些相关性较强的字段带入模型进行建模，测试新特征是否会带来模型效果上的提升：
abs(features_seq_new.corr()['Churn']).sort_values(ascending = False)
#Churn 1.000000
#tenure_year_2019 0.320054
#tenure_year_2014 0.225500
#tenure_month_12 0.194221
#tenure_quarter_4 0.184320
#tenure_quarter_1 0.145929
#tenure_month_1 0.116592
#tenure_year_2015 0.100416
#tenure_month_2 0.075770
#tenure_year_2016 0.059229
#tenure_quarter_2 0.050526
#tenure_year_2017 0.040637
#tenure_month_11 0.038805
#tenure_month_5 0.034115
#tenure_month_4 0.032217
#tenure_month_3 0.027905
#tenure_year_2020 0.023771
#tenure_month_10 0.023090
#tenure_year_2018 0.020308
#tenure_month_7 0.016201
#tenure_month_6 0.014609
#tenure_month_8 0.008940
#tenure_month_9 0.006660
#tenure_quarter_3 0.000203
#Name: Churn, dtype: float64
首先我们带入2014年和2019年两个关键年份字段进行建模：
abs(features_seq_new.corr()['Churn']).sort_values(ascending = False)[1: 3].index
#Index(['tenure_year_2019', 'tenure_year_2014'], dtype='object')
features_new_cols1 = list(abs(features_seq_new.corr()['Churn']).sort_values(ascending = False)[1: 3].index)
features_new_cols1
#['tenure_year_2019', 'tenure_year_2014']
features_new1 = features_seq_new[features_new_cols1]
features_new1
这里我们尝试使用此前定义的features_test函数，用逻辑回归模型对比测试带入新特征之后的模型效果：
features_test(features_new1,
features = features,
labels = labels,
category_cols = category_cols,
numeric_cols = numeric_cols)
#46.48468613624573 s
#(0.8073022312373226,
# {'columntransformer__num': StandardScaler(),
# 'logit_threshold__C': 0.1,
# 'logit_threshold__penalty': 'l1',
# 'logit_threshold__solver': 'saga'},
# accuracy_score recall_score precision_score f1_score \
# train_eval 0.808519 0.681159 0.534496 0.59898
# test_eval 0.797444 0.635556 0.520000 0.57200
#
# roc_auc_score
# train_eval 0.761761
# test_eval 0.738403 )
能够看出，模型效果有了非常显著的提升（原数据集情况下交叉验证的平均准确率为0.8042）。当然，这里我们进一步来进行分析，其实这两个年份字段的根本作用就是给了新入网和最早入网的用户一个标识，本质上也是强化了越早入网越不容易流失这一规律的外在表现。需要注意的是，这种标识其实也是极大的补充了tenure字段在表现“越早入网越不容易流失”这一规律的不足：对于tenure字段来说，尽管数值越大越不容易流失，但tenure字段取值为0时因为统计周期的原因，并没有用户流失：
tcc[['tenure', 'Churn']][tcc['tenure'] == 0]
从这个角度来说，因此2014和2019年份字段从某些角度而言能更好的体现越早入网越不容易流失的规律。
接下来进一步测试第四季度、第一季度以及1月入网这三个新字段对模型效果的影响，在实时预测场景下，相比年份、我们可能更需要关注同一年中的不同月份、不同季节对标签取值的影响：
abs(features_seq_new.corr()['Churn']).sort_values(ascending = False)[4: 7].index
#Index(['tenure_quarter_4', 'tenure_quarter_1', 'tenure_month_1'], dtype='object')
features_new_cols2 = list(abs(features_seq_new.corr()['Churn']).sort_values(ascending = False)[4: 7].index)
features_new_cols2
#['tenure_quarter_4', 'tenure_quarter_1', 'tenure_month_1']
features_new2 = features_seq_new[features_new_cols2]
features_new2
features_test(features_new2,
features = features,
labels = labels,
category_cols = category_cols,
numeric_cols = numeric_cols)
#44.94172239303589 s
#(0.8060851926977689,
# {'columntransformer__num': 'passthrough',
# 'logit_threshold__C': 0.1,
# 'logit_threshold__penalty': 'l2',
# 'logit_threshold__solver': 'newton-cg'},
# accuracy_score recall_score precision_score f1_score \
# train_eval 0.810548 0.675159 0.562547 0.61373
# test_eval 0.794132 0.619543 0.541818 0.57808
#
# roc_auc_score
# train_eval 0.762273
# test_eval 0.732565 )
能看出，这三个新的特征对模型效果提升也是非常明显的，至于为何12月、第四季度入网用户容易流失，而1月、第一季度入网用户更不容易流失，可能和实际营销策略有关，同时我们也可以将该规律反馈给前端运营人员，或据此提出更进一步优化营销策略，但从最终建模效果来看，更细粒度的时间周期划分衍生出来的新特征，确实能够起到一定的作用。同时这也反映出时序字段确实有很多隐藏信息，而更细粒度的时间周期的划分，能够对这些隐藏信息进行有效挖掘。
- 时序字段的二阶特征衍生
当我们更细粒度的对时序特征进行划分后，接下来我们也可以进一步围绕衍生时序特征和原始特征进行双变量或多变量特征衍生，这也是所谓的时序字段的二阶特征衍生。例如在上述例子中，我们已经发现在时序字段衍生字段中，季度是相对重要的特征，那么接下来我们接下来我们可以进一步将季度字段与其他原始字段进行交叉组合、分组统计汇总等，去进行进一步的特征衍生。
1.2 更通用的时序字段基本特征衍生方法
在本案例中，由于时序字段并没有包含更多细节的信息，因此分析过程并不复杂，但在其他很多场景下时序字段的特征衍生与分析可能会非常复杂。因此，为了应对更加复杂场景，我们需要进一步补充一些时序字段的处理方法与特征衍生策略，同时，在对某些包含时序特征的回归问题中，我们还会使用一类仅仅通过时序特征就能够对标签进行预测的模型——时间序列模型，尽管本案例中并不涉及时间序列模型建模，但简单了解其背后的核心思想却是非常有助于我们理解时序特征的重要性，也能够更进一步指导我们进行时序特征的特征衍生。
- Pandas中的时间记录格式
首先是关于时序字段的展示形式，本案例中tenure字段是经过自然数编码后的字段，时间是以整数形式进行呈现，而对于其他很多数据集，时序字段往往记录的就是时间是真实时间，并且是精确到年-月-日、甚至是小时-分钟-秒的字段，例如"2022-07-01;14:22:01"，此时拿到数据后，首先需要考虑的是如何对这类字段进行处理。
t = pd.DataFrame()
t['time'] = ['2022-01-03;02:31:52',
'2022-07-01;14:22:01',
'2022-08-22;08:02:31',
'2022-04-30;11:41:31',
'2022-05-02;22:01:27']
t
当然，对于这类object对象，我们可以字符串分割的方式对其进行处理，此外还有一种更简单通用同时也更有效的方法：将其转化为datetime64格式，这也是pandas中专门用于记录时间对象的格式。对于datetime64来说有两种子类型，分别是datetime64[ns]毫秒格式与datetime64[D]日期格式。无论是哪种格式，我们可以通过pd.to_datetime函数对其进行转化，基本过程如下：
pd.to_datetime?
pd.to_datetime(t['time'])
#0 2022-01-03 02:31:52
#1 2022-07-01 14:22:01
#2 2022-08-22 08:02:31
#3 2022-04-30 11:41:31
#4 2022-05-02 22:01:27
#Name: time, dtype: datetime64[ns]
t['time'] = pd.to_datetime(t['time'])
t['time']
#0 2022-01-03 02:31:52
#1 2022-07-01 14:22:01
#2 2022-08-22 08:02:31
#3 2022-04-30 11:41:31
#4 2022-05-02 22:01:27
#Name: time, dtype: datetime64[ns]
这里需要注意，一般来说时间字段的记录格式都是用’-‘来划分年月日，用’:'来分割时分秒，用空格、分号或者换行来分割年月日与时分秒，这是一种通用的记录方法，如果是手动输入时间，也尽可能按照上述格式进行记录。
同时我们发现，该函数会自动将目标对象转化为datetime64[ns]类型，该对象类型是一种高精度、精确到纳秒（10的负九次方秒）的时间记录格式，后面在进行时间差计算时会看到纳秒级运算的结果。当然，如果我们的时间记录格式本身只精确到日期、并没有时分秒，通过pd.to_datetime函数仍然会转化为datetime64[ns]类型，只是此时显示的时间中就没有时分秒：
t1 = pd.DataFrame()
t1['time'] = ['2022-01-03', '2022-07-01',]
t1
t1['time'] = pd.to_datetime(t1['time'])
t1['time']
#0 2022-01-03
#1 2022-07-01
#Name: time, dtype: datetime64[ns]
就类似于浮点数与整数，更高的精度往往会导致更大的计算量，对于本身只是精确到日期的时间记录格式，我们其实可以用另一种只能精确到天的时间数据格式进行记录，也就是datetime64[D]类型。当然在pd.to_datetime函数使用过程中是无法直接创建datetime64[D]类型对象的，我们需要使用.value.astype(‘datetime64[D]’)的方法对其进行转，但是需要注意，这个过程最终创建的对象类型是array，而不再是Series了：
t1['time'].values
#array(['2022-01-03T00:00:00.000000000', '2022-07-01T00:00:00.000000000'],
# dtype='datetime64[ns]')
t1['time'].values.astype('datetime64[D]')
#array(['2022-01-03', '2022-07-01'], dtype='datetime64[D]')
能够看出，array是支持datetime64[ns]和datetime64[D]等多种类型存储的，但对于pandas来说，只支持以datetime64[ns]类型进行存储，哪怕输入的对象类型是datetime64[D]，在转化为Series时仍然会被转化为datetime64[ns]：
t1['time'] = pd.Series(t1['time'].values.astype('datetime64[D]'), dtype='datetime64[D]')
t1['time']
#0 2022-01-03
#1 2022-07-01
#Name: time, dtype: datetime64[ns]
尽管我们无法使用.values.astype(‘datetime64[D]’)方法将Series对象类型进行’datetime64[D]'类型转化，但不同时间格式的转化有的时候有助于我们控制时间记录本身的精度，例如对于t中的time列，如果对其进行精确到天的’datetime64[D]'类型转化，则会自动删除时分秒的数据记录结果：
t['time'].values.astype('datetime64[D]')
#array(['2022-01-03', '2022-07-01', '2022-08-22', '2022-04-30',
# '2022-05-02'], dtype='datetime64[D]')
t['time-D'] = t['time'].values.astype('datetime64[D]')
t
有的时候我们无需考虑时分秒的时间时，可以通过上述方法进行精确到天的时间格式转化。当然，此外还有’datetime64[h]'类型可精确到小时、'datetime64[s]'精确到、'datetime64[ms]'精确到毫秒等：
t['time'].values.astype('datetime64[h]')
#array(['2022-01-03T02', '2022-07-01T14', '2022-08-22T08', '2022-04-30T11',
# '2022-05-02T22'], dtype='datetime64[h]')
t['time'].values.astype('datetime64[s]')
#array(['2022-01-03T02:31:52', '2022-07-01T14:22:01',
# '2022-08-22T08:02:31', '2022-04-30T11:41:31',
# '2022-05-02T22:01:27'], dtype='datetime64[s]')
在绝大多数情况下，我们都建议采用pandas中datetime类型记录时间（尽管从表面上来看也可以用字符串来表示时间），这也将极大程度方便我们后续对关键时间信息的提取。
- 时序字段的通用信息提取方式
在转化为datetime64格式之后，我们就可以通过一些dt.func方式来提取时间中的关键信息，如年、月、日、小时、季节、一年的第几周等，常用方法如下所示：
t = pd.DataFrame()
t['time'] = ['2022-01-03;02:31:52',
'2022-07-01;14:22:01',
'2022-08-22;08:02:31',
'2022-04-30;11:41:31',
'2022-05-02;22:01:27']
t
t['time']
#0 2022-01-03;02:31:52
#1 2022-07-01;14:22:01
#2 2022-08-22;08:02:31
#3 2022-04-30;11:41:31
#4 2022-05-02;22:01:27
#Name: time, dtype: object
t['time']=pd.to_datetime(t['time'])
t['time']
#0 2022-01-03 02:31:52
#1 2022-07-01 14:22:01
#2 2022-08-22 08:02:31
#3 2022-04-30 11:41:31
#4 2022-05-02 22:01:27
#Name: time, dtype: datetime64[ns]
t['time'].dt.year
#0 2022
#1 2022
#2 2022
#3 2022
#4 2022
#Name: time, dtype: int64
t['time'].dt.second
#0 52
#1 1
#2 31
#3 31
#4 27
#Name: time, dtype: int64
接下来我们用不同的列记录这些具体时间信息：
t['year'] = t['time'].dt.year
t['month'] = t['time'].dt.month
t['day'] = t['time'].dt.day
t['hour'] = t['time'].dt.hour
t['minute'] = t['time'].dt.minute
t['second'] = t['time'].dt.second
t
- 时序字段的其他自然周期提取方式
当然，除了用不同的列记录时序字段的年月日、时分秒之外，我们知道，还有一些自然周期也会对结果预测有较大影响，如日期所在季度。这里需要注意的是，对于时序字段，往往我们会尽可能的对其进行自然周期的划分，然后在后续进行特征筛选时再对这些衍生字段进行筛选，对于此前的数据集，我们能够清晰的看到季度特征对标签的影响，而很多时候，除了季度，诸如全年的第几周、一周的第几天，甚至是日期是否在周末，具体事件的时间是在上午、下午还是在晚上等，都会对预测造成影响。对于这些自然周期提取方法，有些自然周期可以通过dt的方法自动计算，另外则需要手动进行计算。首先我们先看能够自动完成计算的自然周期：
t
t['time'].dt.weekofyear
#0 1
#1 26
#2 34
#3 17
#4 18
#Name: time, dtype: int64
t['time'].dt.quarter
#0 1
#1 3
#2 3
#3 2
#4 2
#Name: time, dtype: int64
t['time'].dt.dayofweek
#0 0
#1 4
#2 0
#3 5
#4 0
#Name: time, dtype: int64
这里需要注意，每周一是从0开始计数，这里我们可以手动+1，对其进行数值上的修改：
t['time'].dt.dayofweek + 1
#0 1
#1 5
#2 1
#3 6
#4 1
#Name: time, dtype: int64
接下来我们将其拼接到原始数据集中：
t['quarter'] = t['time'].dt.quarter
t['weekofyear'] = t['time'].dt.weekofyear
t['dayofweek'] = t['time'].dt.dayofweek + 1
t
接下来继续创建是否是周末的标识字段：
(t['dayofweek'] > 5).astype(int)
#0 0
#1 0
#2 0
#3 1
#4 0
#Name: dayofweek, dtype: int32
t['weekend'] = (t['dayofweek'] > 5).astype(int)
进一步创建小时所属每一天的周期，凌晨、上午、下午、晚上，周期以6小时为划分依据：
(t['hour'] // 6).astype(int)
#0 0
#1 2
#2 1
#3 1
#4 3
#Name: hour, dtype: int32
t['hour_section'] = (t['hour'] // 6).astype(int)
其中，0代表凌晨、1代表上午、2代表下午、3代表晚上。接下来查看时间信息衍生后的数据表：
t
至此，我们就完成了围绕时序字段的详细信息衍生（年月日、时分秒单独提取一列），以及基于自然周期划分的时序特征衍生（第几周、周几、是否是周末、一天中的时间段）。
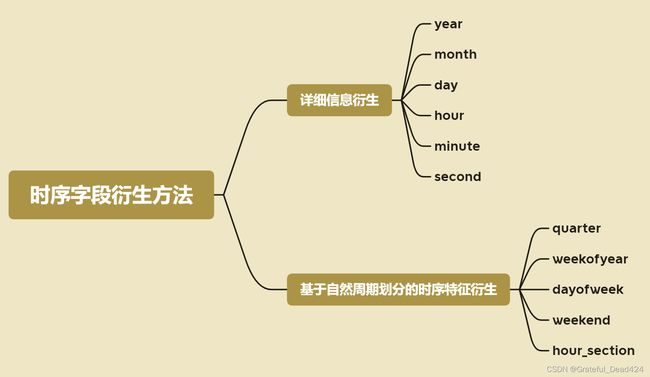
当然整个时序字段的特征衍生过程并不复杂，接下来我们重点探讨为何我们需要对时序特征进行周期性划分，或者说，为何对时序特征进行有效的周期性划分是我们进一步挖掘时序特征背后有效信息的必要手段。
1.3 时序字段特征衍生的本质与核心思路
- 时序字段衍生的本质：增加分组
首先，通过观察我们不难发现，时序特征的衍生其本质上就是对用户进行了更多不同维度的分组，该过程可以通过下图进行解释，在tenure时序特征进行特征衍生后，ID1-6号用户在所属年份列中就被划分到了2019年组中，即他们同为2019年入网的用户，而根据入网的季节进行划分，则ID为0、4、5的三个用户会被划归到第一季度入网用户组中，并且时序特征衍生的字段越多、对用户分组的维度也就越多：
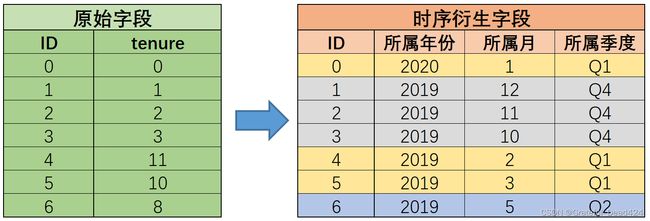
而对用户进行分组之所以能够帮助模型进行建模与训练，其根本原因也是因为有的时候，同一组内（或者是多组交叉）的用户会表现出相类似的特性（或者规律），从而能够让模型更快速的对标签进行更准确的预测，例如假设数据集如下所示，在原始数据集看来，标签取值毫无规律可言，但当我们对其进行时序特征的特征衍生后，立刻能发掘很多规律，例如第四季度用户都流失了、其二是2019年第一季度用户流失都流失了等等，同样，这些通过观察就能看到的规律，也很快会被模型捕捉到，而这也是时序字段衍生能够帮助模型进行更好更快的预测的直观体现：
当然，很多时候也是因为我们不知道什么样的分组能够有效的帮助到模型进行建模，因此往往需要衍生尽可能多的字段，来进行尽可能多的分组，而这些时序字段的衍生字段，也会在后续的建模过程中接受特征筛选的检验。
- 时序字段衍生的核心思路：自然周期和业务周期
而如何才能尽可能的进行更多的时序字段衍生呢？在进行了细节时间特征的衍生之后（划分了年月日、时分秒之后），接下来的时序特征衍生就需要同时结合自然周期和业务周期两个方面进行考虑。所谓自然周期，指的是对于时间大家普遍遵照或者约定俗成的一些规定，例如工作日周末、一周七天、一年四个季度等，这也就是此前我们进行的一系列特征衍生工作，此外其实还可以根据一些业务周期来进行时序特征的划分，例如对于部分旅游景点来说，暑假是旅游旺季，并且很多是以家庭为单位进行出游（学生暑假），因此可以考虑单独将8、9月进行标记，期间记录的用户会有许多共性，而组内用户的共性就将成为后续建模效果的保障；再比如6月、11月是打折季，也可以类似的单独设一列对6月、11月进行标记等等，这些需要特征的衍生，则需要结合具体业务情况来进行判断。
但是，有的时候如果我们能提前判断衍生特征对用户的分组无效，换个更严谨的说法就是，如果我们判断新衍生的特征在对数据分组的过程中，不同组的数据在标签分布上并没有差别，则分组无效，我们大可不必进行如此特征衍生。例如，对于一家普通电商平台用户交易时间的秒和分，从业务角度出发，我们很难说每分钟第一秒交易的用户有哪些共同的特点，或者每小时第二分钟交易的用户有哪些共同的特点，甚至是每分钟的前30秒用户有哪些共同特点、每小时的前半个小时用户呈现出哪些共同的特点等，而这类特征就不必在衍生过程中进行创建了。但是，在另外一些场景下，例如某线下超市的周五，可能就是一个需要重点关注的时间，不仅是因为临近周末很多客户会在下班后进行集中采购、而且很多超市有“黑五”打折的习惯，如果是进行超市销售额预测，是否是周五可能就需要单独标注出来，形成独立的一列（该列被包含在dayofweek的衍生列中）。
大多数情况下关注分和秒都是毫无意义的，某些量化交易场景除外。
总结来看，一方面，我们需要从自然周期和业务周期两个角度进行尽可能多的特征衍生，来提供更多的备选数据分组依据来辅助模型建模，而另一方当面，我们有需要结合当前实际业务情况来判断哪些时序特征的衍生特征是有效的，提前规避掉一些可能并无太大用处的衍生特征。
- 时序字段的补充衍生方法：关键时间点的时间差值衍生
对于时序字段的特征衍生来说，除了自然周期和业务周期衍生外，近些年在竞赛中还涌现了一类时序字段的衍生方法：关键时间点的时间差值特征衍衍生。该方法并不复杂，实际操作过程中需要首先人工设置关键时间点，然后计算每条记录和关键时间点之间的时间差，具体时间差的衡量以天和月为主，当然也可以根据数据集整体的时间跨度为前提进行考虑（例如数据集整体时间记录都是一天当中的不同时间，则时间差的计算可以是小时甚至是分钟）。其中，关键时间点一般来说可以是数据集记录的起始时间、结束时间、距今时间，也可以是根据是根据业务或者数据集本身的数据规律，推导出来的关键时间点。
当然，此前的tenure字段就是距离统计日期截止前的时间差值按月计算的结果
在pandas中我们也可以非常快捷的进行时间差值的计算，我们可以直接将datetime64类型的两列进行相减：
t['time'] - t['time']
#0 0 days
#1 0 days
#2 0 days
#3 0 days
#4 0 days
#Name: time, dtype: timedelta64[ns]
当然，如果是用一列时间减去某个时间的话，我们需要先将这个单独的时间转化为时间戳，然后再进行相减。所谓时间戳，可以简单理解为单个时间的记录格式，在pandas中可以借助pd.Timestamp完成时间戳的创建：
p1 = '2022-01-03;02:31:52'
p1
#'2022-01-03;02:31:52'
pd.Timestamp(p1)
#Timestamp('2022-01-03 02:31:52')
t['time'] - pd.Timestamp(p1)
#0 0 days 00:00:00
#1 179 days 11:50:09
#2 231 days 05:30:39
#3 117 days 09:09:39
#4 119 days 19:29:35
#Name: time, dtype: timedelta64[ns]
其实一个在一个datetime64[ns]类型的Series中，每个元素都是一个时间戳：
t['time']
#0 2022-01-03 02:31:52
#1 2022-07-01 14:22:01
#2 2022-08-22 08:02:31
#3 2022-04-30 11:41:31
#4 2022-05-02 22:01:27
#Name: time, dtype: datetime64[ns]]
t['time'][0]
#Timestamp('2022-01-03 02:31:52')
因此我们也可以将一个datetime64[ns]类型的Series理解成是若干个时间戳组成的Series。
此外，对于Timestamp对象类型，我们同样也可以用year、month、second等时间信息：
pd.Timestamp(p1).year, pd.Timestamp(p1).second
#(2022, 52)
接下来，我们重点讨论时间相减之后的结果。能够发现，上述时间差分的计算结果中，最后返回结果的对象类型是timedelta64[ns]，其中timedelta表示时间差值计算结果（delta往往也见于时间序列的时间差分计算结果的表示中），ns则表示计算结果的精度仍然是纳秒。而具体的差值计算结果也并不难理解，分别表示相差的天数以及时分秒。
td = t['time'] - pd.Timestamp(p1)
td
#0 0 days 00:00:00
#1 179 days 11:50:09
#2 231 days 05:30:39
#3 117 days 09:09:39
#4 119 days 19:29:35
#Name: time, dtype: timedelta64[ns]
接下来，我们可以进一步调用timedelta64[ns]的一些属性，来单独提取相差的天数和相差的秒数：
t['time_diff'] = td
t['time_diff']
#0 0 days 00:00:00
#1 179 days 11:50:09
#2 231 days 05:30:39
#3 117 days 09:09:39
#4 119 days 19:29:35
#Name: time_diff, dtype: timedelta64[ns]
td.dt.days
#0 0
#1 179
#2 231
#3 117
#4 119
#Name: time, dtype: int64
td.dt.seconds
#0 0
#1 42609
#2 19839
#3 32979
#4 70175
#Name: time, dtype: int64
据此我们可以借助相差的天数进一步计算相差的月数:
td.dt.days / 30
#0 0.000000
#1 5.966667
#2 7.700000
#3 3.900000
#4 3.966667
#Name: time, dtype: float64
np.round(td.dt.days / 30).astype('int')
#0 0
#1 6
#2 8
#3 4
#4 4
#Name: time, dtype: int32
这里需要注意，相差的天数是完全忽略时分秒的结果，而相差的秒数则是完全忽略了天数的计算结果，即42609秒代表的是11小时50分9秒的差值，而不包括179天：
11 * 60 * 60 + 50 * 60 + 9
#42609
然后我们将这两列作为新增列拼接到原始特征矩阵中：
t['time_diff_days'] = td.dt.days
t['time_diff_seconds'] = td.dt.seconds
t
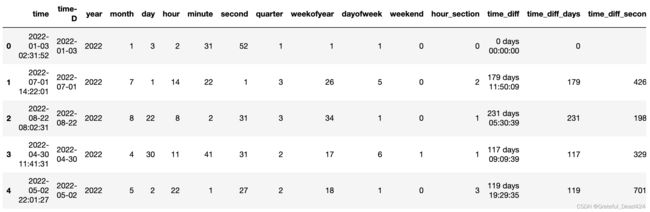
当然，在某些情况下，我们可能会希望计算真实时间差的秒数以及小时数，此时应该怎么做呢？
和datetime类似，timedelta64同样也有timedelta64[h]、timedelta64[s]等对象类型，但pandas中只支持timedelta64[ns]对象类型，我们仍然可以通过.values.astype的方法将时间运算差值转化为timedelta64[h]或timedelta64[s]的array，但再次转化成Series时又会变为timedelta64[ns]：
# 返回纳秒计算结果
td.values
#array([ 0, 15508209000000000, 19978239000000000,
# 10141779000000000, 10351775000000000], dtype='timedelta64[ns]')
td.values.astype('timedelta64[h]')
#array([ 0, 4307, 5549, 2817, 2875], dtype='timedelta64[h]')
td.values.astype('timedelta64[s]')
#array([ 0, 15508209, 19978239, 10141779, 10351775],
# dtype='timedelta64[s]')
注意，这里计算的是真实的时间差：
179 * 24 * 60 * 60 + 11 * 60 * 60 + 50 * 60 + 9
#15508209
但无法保存为Series
pd.Series(td.values.astype('timedelta64[s]'), dtype='timedelta64[s]')
#0 0 days 00:00:00
#1 179 days 11:50:09
#2 231 days 05:30:39
#3 117 days 09:09:39
#4 119 days 19:29:35
#dtype: timedelta64[ns]
当然，我们可以将这些结果保存为整数，然后再作为差值衍生的衍生特征并入原始特征矩阵：
td.values.astype('timedelta64[h]').astype('int')
#array([ 0, 4307, 5549, 2817, 2875])
t['time_diff_h'] = td.values.astype('timedelta64[h]').astype('int')
t['time_diff_s'] = td.values.astype('timedelta64[s]').astype('int')
t
当然，这些已经转化为整数类型的对象是无法（当然也没有必要）进行任何时序方面的操作、如进行自然周期划分、进行时间差值计算等。
而对于关键时间点的时间戳的提取，如数据集起止时间的计算，可以通过min/max方法实现：
t['time'].max()
#Timestamp('2022-08-22 08:02:31')
t['time'].min()
#Timestamp('2022-01-03 02:31:52')
同时，我们可以通过如下方式获取当前时间：
import datetime
datetime.datetime.now()
#datetime.datetime(2022, 2, 18, 16, 52, 31, 407217)
在默认情况下，获得的是精确到毫秒的结果：
pd.Timestamp(datetime.datetime.now())
#Timestamp('2022-02-18 16:53:09.087168')
当然，我们也可以通过如下方式自定义时间输出格式，并借此输出指定精度的时间：
print(datetime.datetime.now().strftime('%Y-%m-%d'))
print(pd.Timestamp(datetime.datetime.now().strftime('%Y-%m-%d')))
#2022-02-18
#2022-02-18 00:00:00
print(datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
print(pd.Timestamp(datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')))
#2022-02-18 20:41:26
#2022-02-18 20:41:26
有了自动获取这些关键时间戳的方法，我们就可以进一步带入进行时间差值的计算了。至此，我们就完成了所有时间特征衍生的简单实践。
1.4 时序字段特征衍生方法汇总
接下来，我们将上述提到的所有方法封装到一个函数中，方便我们后续围绕时序字段进行快速的特征衍生：
def timeSeriesCreation(timeSeries, timeStamp=None, precision_high=False):
"""
时序字段的特征衍生
:param timeSeries：时序特征，需要是一个Series
:param timeStamp：手动输入的关键时间节点的时间戳，需要组成字典形式，字典的key、value分别是时间戳的名字与字符串
:param precision_high：是否精确到时、分、秒
:return features_new, colNames_new：返回创建的新特征矩阵和特征名称
"""
# 创建衍生特征df
features_new = pd.DataFrame()
# 提取时间字段及时间字段的名称
timeSeries = pd.to_datetime(timeSeries)
colNames = timeSeries.name
# 年月日信息提取
features_new[colNames+'_year'] = timeSeries.dt.year
features_new[colNames+'_month'] = timeSeries.dt.month
features_new[colNames+'_day'] = timeSeries.dt.day
if precision_high != False:
features_new[colNames+'_hour'] = timeSeries.dt.hour
features_new[colNames+'_minute'] = timeSeries.dt.minute
features_new[colNames+'_second'] = timeSeries.dt.second
# 自然周期提取
features_new[colNames+'_quarter'] = timeSeries.dt.quarter
features_new[colNames+'_weekofyear'] = timeSeries.dt.weekofyear
features_new[colNames+'_dayofweek'] = timeSeries.dt.dayofweek + 1
features_new[colNames+'_weekend'] = (features_new[colNames+'_dayofweek'] > 5).astype(int)
if precision_high != False:
features_new['hour_section'] = (features_new[colNames+'_hour'] // 6).astype(int)
# 关键时间点时间差计算
# 创建关键时间戳名称的列表和时间戳列表
timeStamp_name_l = []
timeStamp_l = []
if timeStamp != None:
timeStamp_name_l = list(timeStamp.keys())
timeStamp_l = [pd.Timestamp(x) for x in list(timeStamp.values())]
# 准备通用关键时间点时间戳
time_max = timeSeries.max()
time_min = timeSeries.min()
time_now = pd.to_datetime(datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
timeStamp_name_l.extend(['time_max', 'time_min', 'time_now'])
timeStamp_l.extend([time_max, time_min, time_now])
# 时间差特征衍生
for timeStamp, timeStampName in zip(timeStamp_l, timeStamp_name_l):
time_diff = timeSeries - timeStamp
features_new['time_diff_days'+'_'+timeStampName] = time_diff.dt.days
features_new['time_diff_months'+'_'+timeStampName] = np.round(features_new['time_diff_days'+'_'+timeStampName] / 30).astype('int')
if precision_high != False:
features_new['time_diff_seconds'+'_'+timeStampName] = time_diff.dt.seconds
features_new['time_diff_h'+'_'+timeStampName] = time_diff.values.astype('timedelta64[h]').astype('int')
features_new['time_diff_s'+'_'+timeStampName] = time_diff.values.astype('timedelta64[s]').astype('int')
colNames_new = list(features_new.columns)
return features_new, colNames_new
datetime.datetime.now()
#datetime.datetime(2022, 2, 18, 20, 53, 57, 115467)
datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S')
#'2022-02-18 20:53:57'
pd.to_datetime(datetime.datetime.now().strftime('%Y-%m-%d %H:%M:%S'))
#Timestamp('2022-02-18 20:53:57')
其中需要注意，timeStamp时间戳需要以字典形式进行参数传入，字典的key是时间戳的名字/解释，value则是具体表示时间的字符串：
timeStamp = {'p1':'2022-03-25 23:21:52', 'p2':'2022-02-15 08:51:02'}
timeStamp.keys()
#dict_keys(['p1', 'p2'])
timeStamp.values()
#dict_values(['2022-03-25 23:21:52', '2022-02-15 08:51:02'])
则可通过如下表达式创建一个包含了values转换成Timestamp后所组成的list：
[pd.Timestamp(x) for x in list(timeStamp.values())]
#[Timestamp('2022-03-25 23:21:52'), Timestamp('2022-02-15 08:51:02')]
同时，函数定义中用到的zip方法进行的双序列循环，基本过程如下：
a = [1, 2]
b = [3, 4]
for i, j in zip(a, b):
print(i, j)
#1 3
#2 4
list(zip(a, b))
#[(1, 3), (2, 4)]
接下来测试函数效果：
t = pd.DataFrame()
t['time'] = ['2022-01-03;02:31:52',
'2022-07-01;14:22:01',
'2022-08-22;08:02:31',
'2022-04-30;11:41:31',
'2022-05-02;22:01:27']
t
timeStamp = {'p1':'2022-03-25 23:21:52', 'p2':'2022-02-15 08:51:02'}
features_new, colNames_new = timeSeriesCreation(timeSeries=t['time'], timeStamp=timeStamp, precision_high=True)
colNames_new
#['time_year',
# 'time_month',
# 'time_day',
# 'time_hour',
# 'time_minute',
# 'time_second',
# 'time_quarter',
# 'time_weekofyear',
# 'time_dayofweek',
# 'time_weekend',
# 'hour_section', #其中，0代表凌晨、1代表上午、2代表下午、3代表晚上。
# 'time_diff_days_p1', #减了以后.dt.days
# 'time_diff_months_p1',
# 'time_diff_seconds_p1',
# 'time_diff_h_p1', #减了以后.values.astype("timedelta64[h]").astype("int")
# 'time_diff_s_p1',
# 'time_diff_days_p2',
# 'time_diff_months_p2',
# 'time_diff_seconds_p2',
# 'time_diff_h_p2',
# 'time_diff_s_p2',
# 'time_diff_days_time_max', #(t['time']-t["time"].max()).dt.days
# 'time_diff_months_time_max',
# 'time_diff_seconds_time_max',
# 'time_diff_h_time_max',
# 'time_diff_s_time_max',
# 'time_diff_days_time_min',
# 'time_diff_months_time_min',
# 'time_diff_seconds_time_min',
# 'time_diff_h_time_min',
# 'time_diff_s_time_min',
# 'time_diff_days_time_now',
# 'time_diff_months_time_now',
# 'time_diff_seconds_time_now',
# 'time_diff_h_time_now',
# 'time_diff_s_time_now']
features_new
当然，我们也可以进行时间精度更低一级的时序特征衍生：
features_new, colNames_new = timeSeriesCreation(timeSeries=t['time'], timeStamp=timeStamp, precision_high=False)
colNames_new
#['time_year',
# 'time_month',
# 'time_day',
# 'time_quarter',
# 'time_weekofyear',
# 'time_dayofweek',
# 'time_weekend',
# 'time_diff_days_p1',
# 'time_diff_months_p1',
# 'time_diff_days_p2',
# 'time_diff_months_p2',
# 'time_diff_days_time_max',
# 'time_diff_months_time_max',
# 'time_diff_days_time_min',
# 'time_diff_months_time_min',
# 'time_diff_days_time_now',
# 'time_diff_months_time_now']
features_new
至此，我们就完整执行了关于时序特征衍生的全过程。
1.5 时序字段特征的二阶段衍生
所谓时序字段的二阶段衍生，指的是在衍生的时序字段基础上，再次进行特征衍生。不过一般来说，衍生时序字段彼此之间的交叉衍生往往意义不大，例如月份和时间交叉组合衍生，其效果就和以起止日期作为关键时间点计算月份差值效果相同。因此，时序衍生字段的二阶衍生，往往是结合其他字段共同进行，并且，由于时序衍生字段往往变量取值较多，因此往往以分组统计汇总为主，即以时序衍生字段为keycol，对其他字段进行分组汇总统计，往往能起到较好的效果。
更多的时序字段和其他字段的交叉衍生，我们将在后续实践过程中逐步介绍。
2.文本特征衍生方法
接下来，我们进一步讨论关于文本字段的特征衍生方法，也被称为NLP（自然语言处理）特征衍生。当然这里所谓的NLP特征衍生并不是真的去处理文本字段，而是借助文本字段的处理方法与思想，来处理数值型的字段，来衍生出更多有效特征。
关于文本数据的处理技术，我们会在深度学习领域内进行重点探讨。
2.1 语义分析简例
- 词向量转化
在NLP领域中，有一个极为普遍的建模分析场景——语言分析，例如分析一条评论的情感倾向，有文本数据如下：
当然，要让计算机来进行情感倾向的识别，我们就需要考虑把这些文本用数值进行表示，例如我们可以用1表示正面情感、0表示负面情感，也就是说数据集标签是一个二分类的离散变量。那么数据集的特征，也就是一条条文本评论，应该如何表示成一串数字呢？或者换而言之，就是我们如何通过一串数字来描述一段文字呢？最常见的方法就是词袋法，用一个词向量来表示一条文本。
我们都知道，构成一句话语义的基本单位就是单词，而词袋法的基本思想是通过对每段文本进行不同单词的计数，然后用这些计数的结果来构成一个词向量，并借此来表示一个文本。这个过程其实并不复杂，其基本流程是先对原始文本进行分词，找出每段文本或者每句文本都包含哪些单词，然后将这些单词构成语料库，并根据这些计数结果来构建词向量。例如对于上述简短的文本，词向量转化过程如下：
有了这个转化我们就将原来的文本语义识别变成了一个二分类问题，而数据集也转化为了结构化数据，其中特征就是每个出现在文本中的单词，而特征的取值就是单词出现的频率。而后我们即可带该数据集进入模型进行训练与预测。
实际在进行词向量转化的过程中，还会遇到例如文本如何读取、语句应该如何分词等具体技术问题，这些内容并不是本节讨论的重点。
- CountVectorizer与词向量转化
上述词向量的转化方式，也被称为CountVectorizer，词频词向量转化方法。而在NLP领域中，所有依据分词结果转化为向量的过程都被称为词向量转化，因此CountVectorizer也可以理解为词向量转化方式的一种。同时，我们通过观察不难发现，词向量的转化过程其本质就是一个对序列进行有效信息提取的过程，这里指的有效信息实际上就是指对后续建模有帮助的信息。在很多NLP的情境下下，词频其实就代表着语义的倾向，例如出现了“很好”时（“很好”词频为1）时则表示用户对产品的正面肯定，而出现了“一般”时则表示用户对产品并不满意。此外，如果一句话（也就是一段文本）中重复出现了某些单词，则很有可能表示强调的含义。不管怎样，我们对不同单词的词频的统计，其实是希望从一段文本中提取有效信息，或者说提取有效信息，是所有词向量化共同的目标。
- CountVectorizer的sklearn实现
当然，CountVectorizer的过程也可以在sklearn中快速实现：
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
vectorizer
#CountVectorizer()
CountVectorizer?
corpus = ['This is the first document.',
'This is the second second document.',
'And the third one.',
'Is this the first document?']
直接调用fit_transform方法即可对输入的序列进行词频统计
X = vectorizer.fit_transform(corpus)
X.toarray()
#array([[0, 1, 1, 1, 0, 0, 1, 0, 1],
# [0, 1, 0, 1, 0, 2, 1, 0, 1],
# [1, 0, 0, 0, 1, 0, 1, 1, 0],
# [0, 1, 1, 1, 0, 0, 1, 0, 1]])
当然，我们还可以调用vectorizer评估器的get_feature_names属性来查看每一列统计的是哪个单词：
vectorizer.get_feature_names()
#['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third', 'this']
最终，我们可以将其转化为一个列名称为单词名称、数字为单词出现的次数、行数代表每个文本的DataFrame:
c1 = pd.DataFrame(X.toarray(), columns=vectorizer.get_feature_names())
c1
- TF-IDF：词频-逆向词频统计
除了CountVectorizer外，词向量化的常用方法还有TF-IDF，也就是所谓的词频-逆向词频统计。我们知道，CountVectorizer是简单的单词计数，单词出现的次数越高、我们往往就认为该单词对文本的表意就起到了越关键的作用。但有的时候情况恰好相反，例如一些语气助词，“啊、呀”等，再比如中文里面的“的”，这些在文本经常出现的单词，可能恰好对文本表意的识别起不到任何有效作用，也就是说，有的时候简单的词频统计结果无法体现单词对文本表意的重要性。若要降低这些出现频率很高但又没什么用的单词的数值权重，就需要使用另一种词向量转化方法——TF-IDF。
在很多时候，我们都会用term代表分词的结果（即一个个单词），用document代表一段文本
TF-IDF也同样是基于单词的词向量转化，同样也需要对文本进行分词，所不同的是分词后的计算过程。我们通过如下示例来介绍TF-IDF的计算过程。同样还是基于此前定义的文本：
corpus = ['This is the first document.',
'This is the second second document.',
'And the third one.',
'Is this the first document?']
corpus
#['This is the first document.',
# 'This is the second second document.',
# 'And the third one.',
# 'Is this the first document?']
通过调用sklearn中的TfidfTransformer评估器来完成TF-IDF的计算。sklearn中TF-IDF计算过程和CountVectorizer计算过程完全一致，我们先看下计算结果，然后再来介绍计算公式：
from sklearn.feature_extraction.text import TfidfTransformer
TfidfTransformer?
transformer = TfidfTransformer(smooth_idf=False)
tfidf = transformer.fit_transform(c1)
tfidf.toarray()
#array([[0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685],
# [0. , 0.24014568, 0. , 0.24014568, 0. ,
# 0.89006176, 0.18649454, 0. , 0.24014568],
# [0.56115953, 0. , 0. , 0. , 0.56115953,
# 0. , 0.23515939, 0.56115953, 0. ],
# [0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685]])
tfidf.toarray()[0]
#array([0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685])
能够看出，TF-IDF同样也是针对每个单词进行的某种统计量的计算，也就是说tfidf.toarray()[0]同样也是针对第一条文本、总共九个不同单词的某种统计量的计算，只不过此时计算的不再是单词出现的次数。TF-IDF的计算总共分为两部分，其一是TF（term frequency），也就是每个单词出现的次数，和vectorizer结果一致，这里用 t f ( d , t ) tf(d,t) tf(d,t)表示；第二部分是IDF（inverse document frequency），也就是所谓的逆向文件频率，指的是包含该单词的文本占总文本的比例的倒数，用 i d f ( t ) idf(t) idf(t)表示。而TF-IDF就是二者的乘积：
T F − I D F = t f ( d , t ) ∗ i d f ( t ) TF-IDF=tf(d,t)*idf(t) TF−IDF=tf(d,t)∗idf(t) t f ( d , t ) tf(d,t) tf(d,t)的计算过程无需多言，我们重点看下 i d f ( t ) idf(t) idf(t)的计算过程：
i d f ( t ) = l o g [ n d f ( t ) ] idf(t) = log[\frac{n}{df(t)}] idf(t)=log[df(t)n]其中n表示文本总数（也就是总行数）， () 表示单词t出现的次数， ()/ 表示的是包含t单词的文本出现的频率，反过来则是逆向频率，而外面嵌套log则是为了一定程度上进行数值压缩。这是一般情况下的 () 计算过程，但需要注意的是，sklearn中 () 过程会在log结果后加1，过程如下：
i d f ( t ) = l o g [ n d f ( t ) ] + 1 idf(t) = log [ \frac{n}{df(t)} ] + 1 idf(t)=log[df(t)n]+1此时，若 () 趋近n，即 () 趋近1时， [()]+1 仍然可以输出一个大于1的值。
据此，我们手动复现上述TF-IDF计算过程。其中c1就是原文本 t f ( d , t ) tf(d,t) tf(d,t)的计算结果：
c1
而 i d f ( t ) idf(t) idf(t)可以通过如下方式进行计算。首先，c1中总共是n行m个特征，即n个文本、m个单词：
n, m = c1.shape
n, m
#(4, 9)
然后我们可以通过如下方式计算每个单词所在文本出现的次数：
(c1.values[:, 0] != 0).sum()
#1
[(c1.values[:, i] != 0).sum() for i in range(m)]
#[1, 3, 2, 3, 1, 1, 4, 1, 3]
df = np.array([(c1.values[:, i] != 0).sum() for i in range(m)])
则idf计算结果如下：
idf = (np.log(n / df)) + 1
idf
#array([2.38629436, 1.28768207, 1.69314718, 1.28768207, 2.38629436,
# 2.38629436, 1. , 2.38629436, 1.28768207])
TF-IDF计算结果如下：
tfidf1 = c1 * idf
tfidf1
注意这里用到了一个广播运算，即c1是(4,9)的二维数组，而idf是(9,)的一维数组，在进行计算时，会自动将c1中的每一行与idf相乘。
但通过观察我们发现，手动计算的tfidf1与sklearn此前的tfidf略有差异：
tfidf.toarray()
#array([[0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685],
# [0. , 0.24014568, 0. , 0.24014568, 0. ,
# 0.89006176, 0.18649454, 0. , 0.24014568],
# [0.56115953, 0. , 0. , 0. , 0.56115953,
# 0. , 0.23515939, 0.56115953, 0. ],
# [0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685]])
原因是在sklearn中TF-IDF的计算过程还需对最后的计算结果进行归一化操作，也就是normalize处理。注意这里的归一化并不是此前所说的标准化，而是按行进行l1正则化或者l2正则化，默认情况下是进行l2正则化：
from sklearn.preprocessing import normalize
normalize(tfidf1)
#array([[0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685],
# [0. , 0.24014568, 0. , 0.24014568, 0. ,
# 0.89006176, 0.18649454, 0. , 0.24014568],
# [0.56115953, 0. , 0. , 0. , 0.56115953,
# 0. , 0.23515939, 0.56115953, 0. ],
# [0. , 0.43306685, 0.56943086, 0.43306685, 0. ,
# 0. , 0.33631504, 0. , 0.43306685]])
能够看到，处理后的结果即和评估器输出结果一致了。这里需要注意，所谓的按行进行l2正则化，实际计算过程如下：
v n o r m = v ∣ ∣ v ∣ ∣ 2 = v v 1 2 + v 2 2 + ⋯ + v n 2 v_{norm} = \frac{v}{||v||_2} = \frac{v}{\sqrt{v{_1}^2 + v{_2}^2 + \dots + v{_n}^2}} vnorm=∣∣v∣∣2v=v12+v22+⋯+vn2v
这里之所以需要按行进行归一化处理，表面上来看是为了进一步控制每一行数据的取值，实际上是对每个词向量的长度转化为单位范数，方便后续进行词向量的相似度衡量等计算。
此外，sklearn的TF-IDF的计算过程中还有额外的平滑性选项，即可以在实例化评估器时选择smooth_idf为True：
transformer = TfidfTransformer(smooth_idf=True)
此时idf计算过程如下：
i d f ( t ) = l o g [ n + 1 d f ( t ) + 1 ] + 1 idf(t) = log [ \frac{n+1}{df(t)+1} ] + 1 idf(t)=log[df(t)+1n+1]+1其目的是一定程度上削弱分子分母的数值差异，从而让idf整体输出的数值结果更加平稳：
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(c1)
tfidf.toarray()
#array([[0. , 0.43877674, 0.54197657, 0.43877674, 0. ,
# 0. , 0.35872874, 0. , 0.43877674],
# [0. , 0.27230147, 0. , 0.27230147, 0. ,
# 0.85322574, 0.22262429, 0. , 0.27230147],
# [0.55280532, 0. , 0. , 0. , 0.55280532,
# 0. , 0.28847675, 0.55280532, 0. ],
# [0. , 0.43877674, 0.54197657, 0.43877674, 0. ,
# 0. , 0.35872874, 0. , 0.43877674]])
pd.DataFrame(tfidf.toarray(), columns=vectorizer.get_feature_names())
c1
接下来我们简单对比原始文本在CountVectorizer和TF-IDF下的计算结果：
corpus
#['This is the first document.',
# 'This is the second second document.',
# 'And the third one.',
# 'Is this the first document?']
c1
pd.DataFrame(tfidf.toarray(), columns=c1.columns)
能够发现，经过TF-IDF处理之后，某些高频词汇在每一行文本中的相对权重确实有所降低。
此外，我们也可以直接针对原始文本进行TF-IDF进行计算，此时需要使用TfidfVectorizer评估器：
from sklearn.feature_extraction.text import TfidfVectorizer
TfidfVectorizer?
transformer = TfidfVectorizer()
tfidf = transformer.fit_transform(corpus)
tfidf.toarray()
#array([[0. , 0.43877674, 0.54197657, 0.43877674, 0. ,
# 0. , 0.35872874, 0. , 0.43877674],
# [0. , 0.27230147, 0. , 0.27230147, 0. ,
# 0.85322574, 0.22262429, 0. , 0.27230147],
# [0.55280532, 0. , 0. , 0. , 0.55280532,
# 0. , 0.28847675, 0.55280532, 0. ],
# [0. , 0.43877674, 0.54197657, 0.43877674, 0. ,
# 0. , 0.35872874, 0. , 0.43877674]])
transformer.get_feature_names()
#['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third', 'this']
pd.DataFrame(tfidf.toarray(), columns=transformer.get_feature_names())
2.2 NLP特征衍生的简单应用
正所谓“他山之石、可以攻玉”，很多时候NLP特征衍生能够在结构化数据处理中起到意想不到的效果。在了解了NLP中基本的CountVectorizer和TF-IDF方法之后，接下来进一步考虑如何将这些方法应用到结构化数据的特征衍生中。
2.2.1 CountVectorizer与分组统计特征衍生
- 基本原理
先看一个最简单的应用场景，即CountVectorizer在分组统计特征衍生中的应用。我们先从一个例子入手进行观察特征衍生的过程，然后再讨论其背后的本质及原理。当然，在这个例子中，与其说是借助了CountVectorizer进行了特征衍生，不如说CountVectorizer和我们此前介绍的方法殊途同归。
在电信用户数据集中，存在一些彼此“类似”但又相互补充的离散字段，即用户购买服务字段，这些字段记录了用户此前购买的一系列服务，包括是否开通网络安全服务（OnlineSecurity）、是否开通在线备份服务（OnlineBackup）、是否开通设备安全服务（DeviceProtection）等，这些字段都是二分类字段，假设有如下极简数据集：
接下来，我们将上述数据集类比于一个文本。这里首先将OnlineSecurity、OnlineBackup和DeviceProtection视作文本中的不同单词（Term），并根据tenure不同取值对用户进行分组，每个分组视作一个Document，则可将原数据集转化为文本数据，然后再使用CountVectorizer进行计算，该过程也非常简单，就是对每个文件进行词频的汇总，也就是分成两组后进行OnlineSecurity、OnlineBackup和DeviceProtection三个字段的汇总，基本过程如下：
最终，即可衍生出分组统计量OnlineSecurity_count、OnlineBackup_count和DeviceProtection_count。当然，这只是一个非常见的示例，并且如果从最后的结果上来看，其实就是分组求和的结果，但我们仍然需要熟悉这个先把结构化数据转化为文本数据、然后再使用NLP方法进行统计量计算的过程，以便于我们后续在这个过程中引入其他NLP方法以及进行其他形式的分组。
- 代码实现
具体的代码实现过程也非常简单，我们只需要对其进行分组求和集合，可以通过group过程快速实现。
首先先进行数据集的准备工作：
tar_col = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection']
keycol = 'tenure'
features[tar_col].head(5)
但根据此前介绍，这些特征其实都有三个取值：
features[tar_col].nunique()
#OnlineSecurity 3
#OnlineBackup 3
#DeviceProtection 3
#dtype: int64
features['OnlineSecurity'].explode().value_counts().to_dict()
#{'No': 3498, 'Yes': 2019, 'No internet service': 1526}
我们需要将购买了服务标记为1，其他标记为0，可以通过如下操作实现：
(features['OnlineSecurity'] == 'Yes') * 1
#0 0
#1 1
#2 1
#3 1
#4 0
# ..
#7038 1
#7039 0
#7040 1
#7041 0
#7042 1
#Name: OnlineSecurity, Length: 7043, dtype: int64
然后需要将这些列放到一个df中：
features_OE = pd.DataFrame()
features_OE[keycol] = features[keycol]
for col in tar_col:
features_OE[col] = (features[col] == 'Yes') * 1
features_OE.head(5)
在准备好数据集之后，接下来使用groupby的方法、通过sum的方式计算组内求和结果：
count = features_OE.groupby(keycol).sum()
count
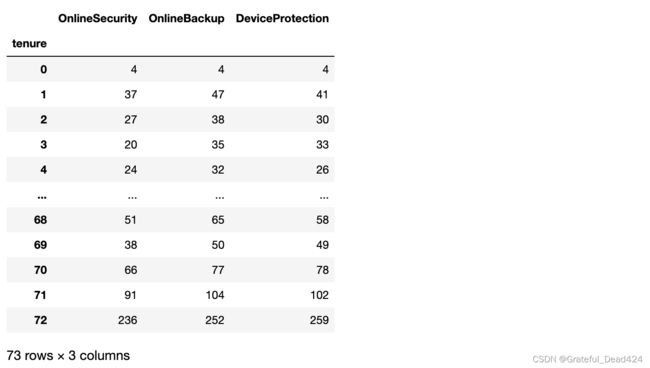
整体过程并不复杂，和分组汇总统计特征一样，稍后我们将这些特征以tenure为主键拼接回原特征矩阵即可形成衍生特征。
2.2.2 T-IDF与分组统计特征衍生
- 特征衍生过程
既然有CountVectorizer计算结果，自然而然我们就会联想到，接下来可以继续进行TF-IDF计算。该计算过程也并不复杂，直接在CountVectorizer结果上进行计算即可。对于上述极简示例，计算结果如下：
c2 = np.array([[1, 2, 2], [2, 1, 0]])
c2
#array([[1, 2, 2],
# [2, 1, 0]])
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(c2)
tfidf.toarray()
#array([[0.27840869, 0.55681737, 0.78258739],
# [0.89442719, 0.4472136 , 0. ]])
据此又可以衍生出新的特征。当然，上述基于原数据集的count结果也可以进行TF-IDF计算：
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(count)
tfidf.toarray()[:5]
#array([[0.57735027, 0.57735027, 0.57735027],
# [0.51021138, 0.64810634, 0.56536936],
# [0.48706002, 0.68549188, 0.5411778 ],
# [0.38390615, 0.67183577, 0.63344515],
# [0.50306617, 0.67075489, 0.54498835]])
据此，我们就又完成了基于TF-IDF的特征衍生。
2.3 NLP特征衍生的本质及方法有效性讨论
NLP特征衍生过程并不复杂，接下来我们进一步在理论层面进行NLP特征有效性的探讨。尽管在特征衍生阶段，我们可以遵照“多多益善”的原则尽创建尽可能多的特征，但一定程度的预判特征是否有效，则可大幅缩短不断尝试创建与筛选特征所耗费的时间。同时对于NLP特征衍生本质的理解，也将有助于实现对这一高级方法的活学活用。
- 序列对象的信息提取
通过观察此前的计算过程我们不难发现，其实无论是CountVectorizer和TF-IDF，归根结底都是对某个序列进行某种层面的信息提取，在文本情况下，就是对分词的结果进行某种层面的统计计算、如果是针对数值变量，则是针对数值变量本身进行某种统计，这两种过程并无本质的区别，这也是CountVectorizer和TF-IDF方法能够迁移的根本原因。
- CountVectorizer特征衍生
那么具体到CountVectorizer方法，我们知道，CountVectorizer的提取的是单词的频次信息，对应到此前举例的数值型离散变量时，CountVectorizer提取的就是组内离散变量取值为1时的累加结果。对于文本对象来说，单词出现的频率越高则很有可能代表该单词对文本的表意越重要，这也是CountVectorizer经常被使用的最根本原因。但需要注意的是，这一点在数值型对象上不一定成立。从最终结果上来看，分组统计CountVectorizer其本质就是进行分组sum计算（前提是原特征必须是二分类变量），而sum指标会极大程度收到本组样本数量影响，在很多情况下统计结果的数值分布并不规律。因此，此前介绍分组特征统计衍生时，尽管sum也是一个统计量，但我们并未将其列为通用的统计指标。
例如，我们在原始数据集的count结果上就能发现这一现象，tenure越大组内样本数量越多、三个特征的sum统计结果也越大:
features_OE.groupby(keycol).sum()
features_OE
而特征本身数值分布较大是会很大程度影响模型效果的，正因如此，sum指标并不是一个常见指标。
此处需要注意，有同学可能会觉得如果每一组的样本数量接近，就可以解决sum统计指标的这一缺陷，实际上如果分组的不同组样本数量接近，则均值统计量的效果就和sum效果类似（二者统计量只相差固定倍数）。
此外，count和sum并不是相同的统计量，count是出现总数的计数，相当于是分组样本总数，而sum则是值的累计。
不过，这也并非绝对，有的时候，如果我们希望分组统计的统计量能够一定程度上体现出分组的样本数量大小，则受到样本数量大小影响的统计量，就是值得考虑的分组汇总统计量。例如还是在电信用户数据集中，如果给出的数据不再是一个用户ID对应一行数据，而是一个用户ID对应着多条历史消费记录数据，则在特征工程环节，我们需要对同一个用户的多条记录进行汇总，此时该用户的消费次数本身就变成了一个值得被统计的信息，此时sum指标就应该在考虑范畴内。
- TF-IDF特征衍生
相比CountVectorizer，基于TF-IDF的特征衍生就要常见很多。从该方法原生的NLP环境中来看，TF-IDF本质上也是对一段文本的单词的重要性进行评估，只不过方法不再是只进行简单的计数，而是同时兼顾单词计数结果和单词所在文本出现频率，这种计算方法其实会“科学”很多，例如，如果某单词出现频率很高、并且大多数文本都出现了该单词，则该单词对文本表意的重要性应该也不是很重要。类似的情况也完全适用于表格数据中。还是以上述数据集为例，当我们在进行分组汇总统计时，其实是希望分组的统计量能够更好的表现出本组数据的特点，因此才有类似均值、方差等统计量的计算，同样，TF-IDF也能很好的计算出每一组数据每个二分类离散特征对本组的重要性，例如，OnlineBackup和DeviceProtection对于组1（黄色组）的计数结果都是2，但相比组2（绿色组），很明显DeviceProtection的计数结果更能作为两组的区分（组2的DeviceProtection计数结果为0，换而言之，DeviceProtection是组1独有的），因此最终TF-IDF的计算结果中DeviceProtection的得分比OnlineBackup更高。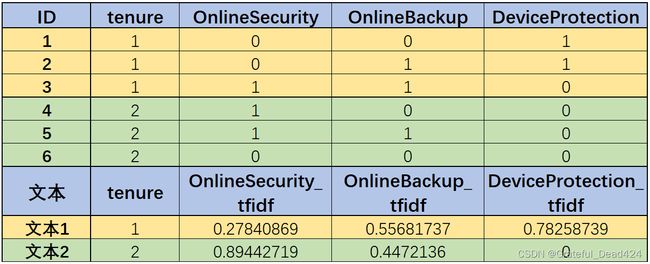
也正因如此，TF-IDF的特征衍生应该是优先考虑的特征衍生方法。
2.4 NLP特征衍生使用场景汇总
接下来我们对分组NLP特征衍生的使用场景进行汇总。当然，这就需要我们首先简单总结NLP特征衍生过程的关键环节。参照此前的极简示例，我们知道，在将NLP方法作用于结构化数据的过程中，我们需要考虑两个关键环节，其一是选择单词（Term）所对应的特征，其二则是划分这些特征的统计范畴，也就是找出单词所在的文本的范畴。例如，在上述极简示例中，我们选择的单词就是’OnlineSecurity’、'OnlineBackup’和’DeviceProtection’这三个字段，而文本划分则是根据tenure的不同取值进行的划分：
这其实是一种非常典型的NLP特征衍生的使用场景，即针对分组后的二分类变量进行统计特征衍生。不过这里有两点需要注意，其一是对变量的选择，如果所选择的变量是二分类变量（或者可以转化为二分类变量的变量），那么这些变量最好是一个事件的不同角度的统计结果，例如上述三个字段其实都是用户某次购买行为在三项不同服务上的记录结果，三个字段相互补充、共同记录了用户购买行为的最终结果（当然，如果是原始数据集，则是要带入所有记录了用户购买服务的字段），这就类似一段文本的不同单词，其出现的频次、相互组合的方式，最终都是为了达到某种表意的效果。此外，有时我们也可以选择多分类的名义变量进行分组统计计算，例如购买商品的品类，可以进行如下类型特征衍生：
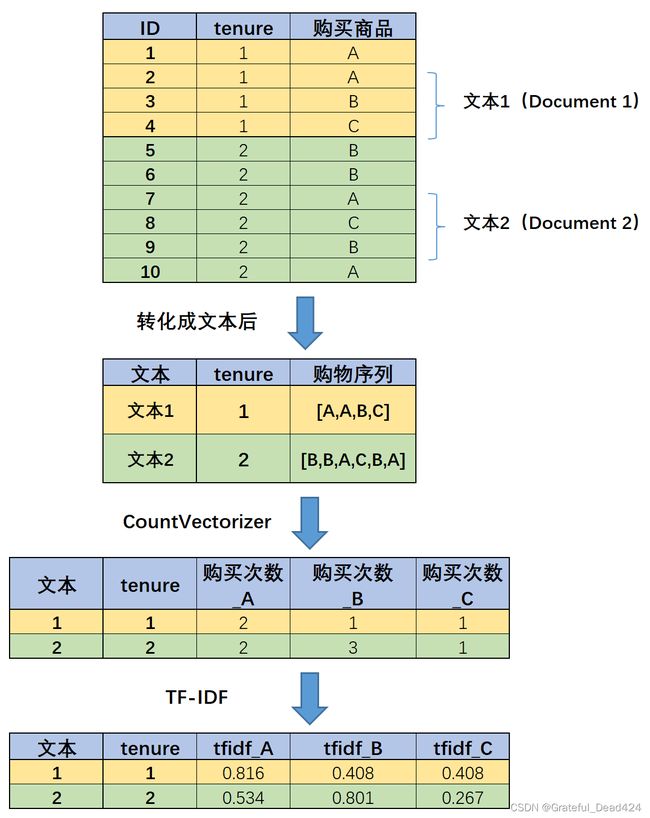
cc = np.array([[2, 1, 1],
[2, 3, 1]])
cc
#array([[2, 1, 1],
# [2, 3, 1]])
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(cc)
tfidf.toarray()
#array([[0.81649658, 0.40824829, 0.40824829],
# [0.53452248, 0.80178373, 0.26726124]])
此时，CountVectorizer的特征衍生结果记录着不同时间段用户对于不同类型商品的喜好程度，而TF-IDF的计算结果则是不同时间段用户独特品味（只有某商品在该时间段频繁出现、而别的时间段没出现，才能在TF-IDF的计算结果中获得高分），当然这肯定也是一个值得统计的特征。
需要注意的是，由于NLP特征衍生都是基于计数的结果，因此如果带入的是有序分类变量，则也会将其视作离散变量进行处理。
第二点需要注意的就是文本划分，不同于其他分组汇总统计特征衍生需要控制分组的数量，NLP特征衍生其实会更适用于分组更多的情况，或者说在单词数量（划分的特征数量）有限的情况下，较短的文本相比较长的文本，更适合使用NLP方法进行处理。（试想一下使用NLP方法对总共只有三个单词、但每个单词都重复出现上百次的文本进行分类。）这也就是说，NLP特征衍生比较适合配合多变量分组特征衍生（或者分组较多的双变量特征衍生）共同进行。这里需要注意一种极端情况，即所有单词在所有文本中都出现，此时TF-IDF的计算结果就是count后normalize的结果，例如此前的例子中，其实就因为分组较少、所有的特征在个分组内的取值都不为0，因此TF-IDF的计算结果和count后normalize的结果一致，该情况下并不能体现TF-IDF的核心优势：
cc
#array([[2, 1, 1],
# [2, 3, 1]])
tfidf.toarray()
#array([[0.81649658, 0.40824829, 0.40824829],
# [0.53452248, 0.80178373, 0.26726124]])
normalize(cc)
#array([[0.81649658, 0.40824829, 0.40824829],
# [0.53452248, 0.80178373, 0.26726124]])
此外对于TF-IDF来说，除了可以进行分组统计，也可以直接对单行数据进行统计和计算，不过此时CountVectorizer过程返回的结果就是原始数据，该部分无需重复计算。
cc = np.array([[0, 0, 1],
[0, 1, 1],
[1, 1, 0],
[1, 0, 1],
[1, 1, 0],
[0, 1, 1]])
cc
#array([[0, 0, 1],
# [0, 1, 1],
# [1, 1, 0],
# [1, 0, 1],
# [1, 1, 0],
# [0, 1, 1]])
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(cc)
tfidf.toarray()
#array([[0. , 0. , 1. ],
# [0. , 0.70710678, 0.70710678],
# [0.7593387 , 0.65069558, 0. ],
# [0.7593387 , 0. , 0.65069558],
# [0.7593387 , 0.65069558, 0. ],
# [0. , 0.70710678, 0.70710678]])
最后，需要注意的是，对单独的列进行TF-IDF计算也是毫无意义的，最终的计算结果是0值归0，其他所有取值都归为1：
cc = np.array([0, 1, 5000]).reshape(-1, 1)
cc
#array([[ 0],
# [ 1],
# [5000]])
transformer = TfidfTransformer(smooth_idf=True)
tfidf = transformer.fit_transform(cc)
tfidf.toarray()
#array([[0.],
# [1.],
# [1.]])
2.5 NLP特征衍生函数编写
接下来考虑通过函数编写，封装整个NLP特征衍生过程。NLP特征衍生过程并不复杂，借助sklearn中相关评估器就能快速实现。定义函数如下：
from sklearn.preprocessing import normalize
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
def NLP_Group_Statistics(features,
col_cat,
keyCol=None,
tfidf=True,
countVec=True):
"""
多变量分组统计特征衍生函数
:param features: 原始数据集
:param col_cat: 参与衍生的离散型变量，只能带入多个列
:param keyCol: 分组参考的关键变量，输入字符串时代表按照单独列分组，输入list代表按照多个列进行分组
:param tfidf: 是否进行tfidf计算
:param countVec: 是否进行CountVectorizer计算
:return：NLP特征衍生后的新特征和新特征的名称
"""
# 提取所有需要带入计算的特征名称和特征
if keyCol != None:
if type(keyCol) == str:
keyCol = [keyCol]
colName_temp = keyCol.copy()
colName_temp.extend(col_cat)
features = features[colName_temp]
else:
features = features[col_cat]
# 定义CountVectorizer计算和TF-IDF计算过程
def NLP_Stat(features=features,
col_cat=col_cat,
keyCol=keyCol,
countVec=countVec,
tfidf=tfidf):
"""
CountVectorizer计算和TF-IDF计算函数
参数和外层函数参数完全一致
返回结果需要注意，此处返回带有keyCol的衍生特征矩阵及特征名称
"""
n = len(keyCol)
col_cat = [x +'_' + '&'.join(keyCol) for x in col_cat]
if tfidf == True:
# 计算CountVectorizer
features_new_cntv = features.groupby(keyCol).sum().reset_index()
colNames_new_cntv = keyCol.copy()
colNames_new_cntv.extend([x + '_cntv' for x in col_cat])
features_new_cntv.columns = colNames_new_cntv
# 计算TF-IDF
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(features_new_cntv.iloc[:, n: ]).toarray()
colNames_new_tfv = [x + '_tfidf' for x in col_cat]
features_new_tfv = pd.DataFrame(tfidf, columns=colNames_new_tfv)
if countVec == True:
features_new = pd.concat([features_new_cntv, features_new_tfv], axis=1)
colNames_new_cntv.extend(colNames_new_tfv)
colNames_new = colNames_new_cntv
else:
colNames_new = pd.concat([features_new_cntv[:, :n], features_new_tfv], axis=1)
features_new = keyCol + features_new_tfv
# 如果只计算CountVectorizer时
elif countVec == True:
features_new_cntv = features.groupby(keyCol).sum().reset_index()
colNames_new_cntv = keyCol.copy()
colNames_new_cntv.extend([x + '_cntv' for x in col_cat])
features_new_cntv.columns = colNames_new_cntv
colNames_new = colNames_new_cntv
features_new = features_new_cntv
return features_new, colNames_new
# keyCol==None时对原始数据进行NLP特征衍生
# 此时无需进行CountVectorizer计算
if keyCol == None:
if tfidf == True:
transformer = TfidfTransformer()
tfidf = transformer.fit_transform(features).toarray()
colNames_new = [x + '_tfidf' for x in col_cat]
features_new = pd.DataFrame(tfidf, columns=colNames_new)
# keyCol!=None时对分组汇总后的数据进行NLP特征衍生
else:
n = len(keyCol)
# 如果是依据单个特征取值进行分组
if n == 1:
features_new, colNames_new = NLP_Stat()
# 将分组统计结果拼接回原矩阵
features_new = pd.merge(features[keyCol[0]], features_new, how='left',on=keyCol[0])
features_new = features_new.iloc[:, n: ]
colNames_new = features_new.columns
# 如果是多特征交叉分组
else:
features_new, colNames_new = NLP_Stat()
# 在原数据集中生成合并主键
features_key1, col1 = Multi_Cross_Combination(keyCol, features, OneHot=False)
# 在衍生特征数据集中创建合并主键
features_key2, col2 = Multi_Cross_Combination(keyCol, features_new, OneHot=False)
features_key2 = pd.concat([features_key2, features_new], axis=1)
# 将分组统计结果拼接回原矩阵
features_new = pd.merge(features_key1, features_key2, how='left',on=col1)
features_new = features_new.iloc[:, n+1: ]
colNames_new = features_new.columns
return features_new, colNames_new
上述函数的列表推导式计算结果如下：
col_cat = ['OnlineBackup', 'DeviceProtection']
keycol = ['tenure', 'OnlineSecurity']
[x +'_' + '&'.join(keycol) for x in col_cat]
#['OnlineBackup_tenure&OnlineSecurity',
# 'DeviceProtection_tenure&OnlineSecurity']
而在使用Multi_Cross_Combination函数进行合并主键创建的过程如下所示
features_OE
接下来，验证该函数的实际使用效果，首先是同时使用’tenure’和’OnlineSecurity’进行多变量分组，对’OnlineBackup’、'DeviceProtection’进行NLP特征衍生过程，计算结果如下：
features_new, colNames_new = NLP_Group_Statistics(features_OE, col_cat, keycol)
features_new
colNames_new
#Index(['OnlineBackup_tenure&OnlineSecurity_cntv',
# 'DeviceProtection_tenure&OnlineSecurity_cntv',
# 'OnlineBackup_tenure&OnlineSecurity_tfidf',
# 'DeviceProtection_tenure&OnlineSecurity_tfidf'],
# dtype='object')
当然，我们也可以验证单变量的衍生效果：
col_cat = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection']
keycol = 'tenure'
features_new, colNames_new = NLP_Group_Statistics(features_OE, col_cat, keycol)
features_new.head()
colNames_new
#Index(['OnlineSecurity_tenure_cntv', 'OnlineBackup_tenure_cntv',
# 'DeviceProtection_tenure_cntv', 'OnlineSecurity_tenure_tfidf',
# 'OnlineBackup_tenure_tfidf', 'DeviceProtection_tenure_tfidf'],
# dtype='object')
以及如果不进行分组，只计算TF-IDF的话结果如下：
col_cat = ['OnlineSecurity', 'OnlineBackup', 'DeviceProtection']
features_new, colNames_new = NLP_Group_Statistics(features_OE, col_cat)
features_new.head()
colNames_new
#['OnlineSecurity_tfidf', 'OnlineBackup_tfidf', 'DeviceProtection_tfidf']
features_new
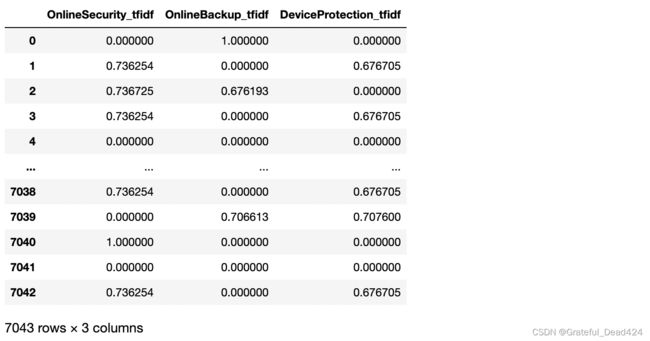
至此，我们即完成了所有NLP特征衍生的内容介绍。
当然，本部分的所有内容也就是目前常用的特征衍生方法的汇总，在本阶段我们介绍而来非常多的特征衍生的方法，其中也定义了非常多的函数。正如此前所说，截止目前，其实并没有非常完整详细的特征衍生的第三方库，因此用好上面定义的函数，后续的建模和实践环节也将如虎添翼。但由于此前定义的函数众多、彼此相互调用的关系也较为复杂，因此我们还将花点时间对上述函数的使用方法、使用过程中的注意事项进行说明，并且在适当的地方进行更高层次的封装，以方便后续调用，同时，我们也将汇总此前介绍的各类方法的使用场景，方便大家参照总结内容按图索骥、也帮助大家加深理解、以进一步做到活学活用。