5.时间序列分析

一.定义：
时间序列分析(Time-Series Analysis)是指将原来的数据分解为四部分来看——长期趋势（secular trend，T）、季节趋势（seasonal variation，S）、循环变动（cyclical variation，C）和不规则变动（irregular variation，I）， 然后综合这些因素， 提出预测。
（1）长期趋势（secular trend，T）：统计指标在长的一段时间内，表现出持续上升或下降的趋势。
（2）季节趋势（seasonal variation，S）：因为季节的转变使数值发生的周期性变动。一般以月、季、周为时间单位。如羽绒服销售情况。
（3）循环变动（cyclical variation，C）：循环变动通常以若干年为周期，在曲线图上表现为波浪式的周期变动。这种周期变动的特征变现为增加和减少交替出现，但是并不具严格规则的周期性连续变动。
（4）不规则变动（irregular variation，I）：由某些随机因素导致的数值变化，这些因素的作用是不可预知和没有规律性的，可以视为由于众多偶然因素对时间序列造成的影响（在回归中又被称为扰动项）。

二.时间序列分解：
1.叠加模型：以上四种变动的加和（波动较稳定）
2.乘积模型：四种变动的乘积（波动越来越大）

三.指数平滑模型
（1）简单指数平滑（不含趋势季节，只能预测一期，存在滞后性）
公式：

x（t+1）为第t+1期的预测值，α为平滑系数。（spss的专家建模器会自动选取）

注：
1.如果时间序列具有不规则的起伏变化，但长期趋势接近一个稳定常数，α值一般较小(取0.05‐0.2之间)
2.如果时间序列具有迅速明显的变化倾向，则α应该取较大值（取0.3‐0.5）
3.如果时间序列变化缓慢，亦应选较小的值（一般在0.1‐0.4之间）

（2）霍特线性趋势模型（线性趋势，不含季节成分）
公式：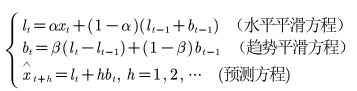
t为当前期，h为预测步长，x（t）为第t期实际观测值，α为水平的平滑参数，β为趋势的平滑参数。

（3）阻尼趋势模型（线性趋势减弱，不含季节成分；在霍特的模型上引入了阻尼效应）
公式：
φ为阻尼系数（取值在01之间）

（4）简单季节性（含稳定季节成分，无趋势）
公式：
m为周期长度（年12，季度4），γ是季节的平滑系数，h为预测步长。

（5）温特斯加法模型（含有稳定的线性趋势，含有稳定的季节成分）
公式：
（6）温特斯乘法模型（含有线性趋势，含有不稳定的季节成分）
公式：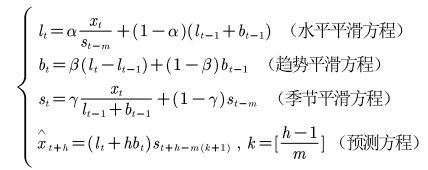

四.时间序列分析的模型（AR,MA,ARMA）：
（1）平稳性验证：若序列均值固定，方差为常数且协方差只与间隔s有关，与t无关，那么称序列弱平稳（一般将弱平稳默认为时间序列中的平稳），白噪声序列是平稳的一个特例，也可以说明平稳性。如下图：

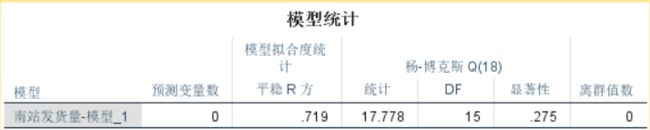
（关于残差与Q检验后面会详细说明）
从残差的ACF和PACF图形中可以看出，所有滞后阶数的ACF和PACF均和0没有显著的差异；对残差进行Q检验得到的p值为0.275>0.05，无法拒绝原假设，认为残差就是白噪声序列，因此此模型能够很好的识别本例中的销量数据。

（2）差分方程与滞后算子：

差分方程：

将某个时间序列变量表示为该变量的滞后项、时间和其他变量的函数，这样的一个函数方程被称为差分方程。
上面的公式均为差分方程。其中，红色部分为差分方程的齐次部分。对于ARMA模型来说，其其次部分组成的特征方程的p个解的模长决定了ARMA模型的y（t）是否平稳。

滞后算子：

用L表示滞后算子。
公式：
（L^i）*y（t）=y（t-i）
满足性质：
ARMA模型的滞后算子表示：

（3）AR（p）模型 （p阶自回归模型）

平稳性：
这里的AR模型是平稳的时间序列模型（不平稳则先转换为平稳）。
若齐次部分的p个解小于1，则为平稳；
若有k个解等于1，则需要经过k阶差分（即ARIMA模型，后文会说）；
若存在解>1，y（t）会爆炸增长。

（4）MA（q）模型 （q阶移动平均过程）

与AR的关系：一阶移动平均模型可以转换为无穷阶的自回归模型，这一性质称为移动平均模型的可逆性；类似的，我们在某些条件下（可逆性条件）也可以将MA(q)模型也转换为无穷阶的自回归过程。
平稳性：
q为常数，则MA（q）模型一定平稳。

（5）ARMA（p，q）模型：
ARMA（p，q）模型为两者的组合形式
因为MA一定平稳，所以我们只需要考虑AR模型的平稳性。（见上文）

（6）p，q的确定的准则，ACF与PACF：

ACF（自相关系数）：
首先假设序列平稳（详细见上文）
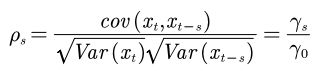视ρs为s的函数，该函数为自相关函数（间隔为s的两个时间点的相关系数）
对于样本来说，样本自相关系数：

PACF（偏自相关系数）：
PACF相当于在计算X(t)和X(t-h)的相关性的时候，挖空在(t-h,t)上所有数据点对X(t)的影响，去反映X(t-h)和X(t)之间真正的相关性。
由α（h）即x（t）与x（t-h）的偏自相关系数（类似回归）。
①对于AR（p）模型。ACF逐渐衰减（拖尾），PACF p阶后截尾。②对于MA（q）模型。ACF q阶后截尾，PACF拖尾。③对于ARMA（p，q）。ACF与PACF均拖尾。
（7）模型的确定，AIC和BIC准则（越小越好）
pq太大会出现过拟合，AIC与BIC本质是为了解决过拟合问题，模型需要在复杂度与易解释程度上寻求平衡。
AIC：赤池信息准则
公式： AIC=2*（参数个数）-2ln（模型的极大似然函数值）
BIC：贝叶斯信息准则
公式： n表示样本的个数；BIC=ln（n）（参数个数）-2*ln（模型的极大似然函数值）
注：AIC与BIC都是越小越好，BIC对于模型复杂程度的惩罚系数更大，因此BIC更简洁

（8）检验模型是否识别完全
估计完成时间序列模型后，我们需要对残差进行白噪声检验。若为白噪声，则模型可识别完全；若残差不是白噪声，则未识别完全，模型需要修正。可以通过Q检验进行上述过程（这里不在赘述，只要p>0.05就为白噪声）

五.时间序列分析的模型（ARIMA）：
ARIMA（p，d，q）模型，即差分自回归移动平均模型。若序列不是平稳的，可能是d阶单位根过程。我们就得先对其就行差分处理，转换为平稳时间序列后再建模。d表示差分的阶数。

联立后移项，得到

六.时间序列分析的模型（SARIMA）：
SARIMA模型，即季节性ARIMA模型。
表示为：（m为周期数，年12季4）
PDQ分别为季节性的AR，差分与MA部分