基于mujoco环境下的ant_v2 ppo算法训练

 一、项目简介

本项目采取action-critic算法与ppo算法相结合的方法对mujoco环境下的ant_v2智能体（对mujoco环境下的其它智能体也试用）进行强化学习训练。

 二、原理详解

 

 三、代码部分（pytorch）

import gym
import torch
import numpy as np
import argparse
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.optim as optim
from collections import deque
import sys

sys.argv = ['run.py']

parser = argparse.ArgumentParser()
parser.add_argument('--env_name', type=str, default="Humanoid-v2",
                    help='name of Mujoco environement')
args = parser.parse_args()

env = gym.make('Ant-v2')
N_S = env.observation_space.shape[0]
N_A = env.action_space.shape[0]
# 初始化随机种子
env.seed(500)
torch.manual_seed(100)
np.random.seed(500)
##状态的归一化

##parameters
lr_actor = 0.0003
lr_critic = 0.0003
Iter = 1500
MAX_STEP = 10000
gamma = 0.98
lambd = 0.98
batch_size = 64
epsilon = 0.2
l2_rate = 0.001


# Actor网络
class Actor(nn.Module):
    def __init__(self, N_S, N_A):
        super(Actor, self).__init__()
        self.fc1 = nn.Linear(N_S, 64)
        self.fc2 = nn.Linear(64, 64)
        self.sigma = nn.Linear(64, N_A)
        self.mu = nn.Linear(64, N_A)
        self.mu.weight.data.mul_(0.1)
        self.mu.bias.data.mul_(0.0)
        # self.set_init([self.fc1,self.fc2, self.mu, self.sigma])
        self.distribution = torch.distributions.Normal

    # 初始化网络参数
    def set_init(self, layers):
        for layer in layers:
            nn.init.normal_(layer.weight, mean=0., std=0.1)
            nn.init.constant_(layer.bias, 0.)

    def forward(self, s):
        x = torch.tanh(self.fc1(s))
        x = torch.tanh(self.fc2(x))

        mu = self.mu(x)
        log_sigma = self.sigma(x)
        # log_sigma = torch.zeros_like(mu)
        sigma = torch.exp(log_sigma)
        return mu, sigma

    def choose_action(self, s):
        mu, sigma = self.forward(s)
        Pi = self.distribution(mu, sigma)
        return Pi.sample().numpy()


# Critic网洛
class Critic(nn.Module):
    def __init__(self, N_S):
        super(Critic, self).__init__()
        self.fc1 = nn.Linear(N_S, 64)
        self.fc2 = nn.Linear(64, 64)
        self.fc3 = nn.Linear(64, 1)
        self.fc3.weight.data.mul_(0.1)
        self.fc3.bias.data.mul_(0.0)
        # self.set_init([self.fc1, self.fc2, self.fc2])

    def set_init(self, layers):
        for layer in layers:
            nn.init.normal_(layer.weight, mean=0., std=0.1)
            nn.init.constant_(layer.bias, 0.)

    def forward(self, s):
        x = torch.tanh(self.fc1(s))
        x = torch.tanh(self.fc2(x))
        values = self.fc3(x)
        return values


class Ppo:
    def __init__(self, N_S, N_A):
        self.actor_net = Actor(N_S, N_A)
        self.critic_net = Critic(N_S)
        self.actor_optim = optim.Adam(self.actor_net.parameters(), lr=lr_actor)
        self.critic_optim = optim.Adam(self.critic_net.parameters(), lr=lr_critic, weight_decay=l2_rate)
        self.critic_loss_func = torch.nn.MSELoss()

    def train(self, memory):
        memory = np.array(memory)
        states = torch.tensor(np.vstack(memory[:, 0]), dtype=torch.float32)

        actions = torch.tensor(list(memory[:, 1]), dtype=torch.float32)
        rewards = torch.tensor(list(memory[:, 2]), dtype=torch.float32)
        masks = torch.tensor(list(memory[:, 3]), dtype=torch.float32)

        values = self.critic_net(states)

        returns, advants = self.get_gae(rewards, masks, values)
        old_mu, old_std = self.actor_net(states)
        pi = self.actor_net.distribution(old_mu, old_std)

        old_log_prob = pi.log_prob(actions).sum(1, keepdim=True)

        n = len(states)
        arr = np.arange(n)
        for epoch in range(1):
            np.random.shuffle(arr)
            for i in range(n // batch_size):
                b_index = arr[batch_size * i:batch_size * (i + 1)]
                b_states = states[b_index]
                b_advants = advants[b_index].unsqueeze(1)
                b_actions = actions[b_index]
                b_returns = returns[b_index].unsqueeze(1)

                mu, std = self.actor_net(b_states)
                pi = self.actor_net.distribution(mu, std)
                new_prob = pi.log_prob(b_actions).sum(1, keepdim=True)
                old_prob = old_log_prob[b_index].detach()
                ratio = torch.exp(new_prob - old_prob)

                surrogate_loss = ratio * b_advants
                values = self.critic_net(b_states)

                critic_loss = self.critic_loss_func(values, b_returns)

                self.critic_optim.zero_grad()
                critic_loss.backward()
                self.critic_optim.step()

                ratio = torch.clamp(ratio, 1.0 - epsilon, 1.0 + epsilon)

                clipped_loss = ratio * b_advants

                actor_loss = -torch.min(surrogate_loss, clipped_loss).mean()

                self.actor_optim.zero_grad()
                actor_loss.backward()

                self.actor_optim.step()

    # 计算GAE
    def get_gae(self, rewards, masks, values):
        rewards = torch.Tensor(rewards)
        masks = torch.Tensor(masks)
        returns = torch.zeros_like(rewards)
        advants = torch.zeros_like(rewards)
        running_returns = 0
        previous_value = 0
        running_advants = 0

        for t in reversed(range(0, len(rewards))):
            # 计算A_t并进行加权求和
            running_returns = rewards[t] + gamma * running_returns * masks[t]
            running_tderror = rewards[t] + gamma * previous_value * masks[t] - \
                              values.data[t]
            running_advants = running_tderror + gamma * lambd * \
                              running_advants * masks[t]

            returns[t] = running_returns
            previous_value = values.data[t]
            advants[t] = running_advants
        # advants的归一化
        advants = (advants - advants.mean()) / advants.std()
        return returns, advants


class Nomalize:
    def __init__(self, N_S):
        self.mean = np.zeros((N_S,))
        self.std = np.zeros((N_S,))
        self.stdd = np.zeros((N_S,))
        self.n = 0

    def __call__(self, x):
        x = np.asarray(x)
        self.n += 1
        if self.n == 1:
            self.mean = x
        else:
            # 更新样本均值和方差
            old_mean = self.mean.copy()
            self.mean = old_mean + (x - old_mean) / self.n
            self.stdd = self.stdd + (x - old_mean) * (x - self.mean)
            # 状态归一化
        if self.n > 1:
            self.std = np.sqrt(self.stdd / (self.n - 1))
        else:
            self.std = self.mean
        x = x - self.mean
        x = x / (self.std + 1e-8)
        x = np.clip(x, -5, +5)
        return x


ppo = Ppo(N_S, N_A)
nomalize = Nomalize(N_S)
episodes = 0
eva_episodes = 0
avg_rewards = []
show_episodes = []
for iter in range(Iter):
    memory = deque()
    scores = []
    steps = 0
    while steps < 2048:  # Horizen
        episodes += 1
        s = nomalize(env.reset())
        score = 0
        for _ in range(MAX_STEP):
            steps += 1
            # 选择行为
            act = ppo.actor_net.choose_action(torch.from_numpy(np.array(s).astype(np.float32)).unsqueeze(0))[0]
            if episodes % 50 == 0:
                env.render()
            s_, r, done, info = env.step(act)
            s_ = nomalize(s_)

            mask = (1 - done) * 1
            memory.append([s, act, r, mask])

            score += r
            s = s_
            if done:
                break
        with open('log_' + args.env_name + '.txt', 'a') as outfile:
            outfile.write('\t' + str(episodes) + '\t' + str(score) + '\n')
        scores.append(score)
        if steps >= 2048:
            show_episodes.append(episodes)
            score_avg = np.mean(scores)
            avg_rewards.append(score_avg)
            plt.clf()
            plt.xlabel('Episodes')
            plt.ylabel('Rewards')
            plt.plot(show_episodes, avg_rewards, color='skyblue', label='Current')
            # plt.plot(self.avg_rewards, color='red', label='Average')
            plt.legend()
            # plt.savefig('Train.jpg')
            plt.show()
            plt.pause(0.001)
    # score_avg = np.mean(scores)
    print('{} episode avg_reward is {:.2f}'.format(episodes, score_avg))
    # 每隔一定的timesteps 进行参数更新
    ppo.train(memory)

三、结果展示

对本项目智能体的训练效果影响较大的超参数主要是action网络以及critic网络的优化器（作者采用的是Adam优化器，默认为0.001）的学习率设定。如下分别展示三种不同类型的超参数设置。

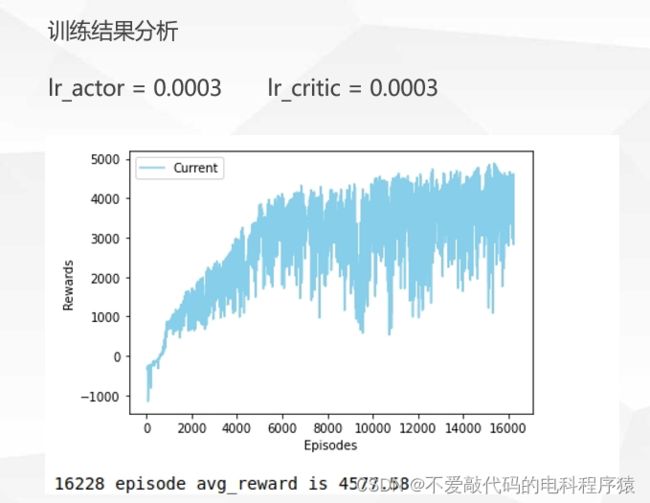
1.效率优先方案

考虑到对本环境下的智能体后期训练时间成本过高，因此综合训练效果和时间消耗考虑，如下的学习率设定较为合适（读者也可自行寻找最佳设定）。在此设定下，每次ant的运动得分已经稳定在三千分以上。

2.效果优先方案

从图上可以看出，优化器学习率达到一个较小值时，智能体的训练效果更加稳定，但随之付出的代价就是训练速度的下降，如果你有充足的时间，可以参考该类型进行设定。

 3.失败案例

如果过分采用greedy思想，过高的学习率往往会产生不可逆的权重设定（训练的神经网络非常垃圾）。在前期训练轮次中reward上涨速度很快，但上限低，且后期极有可能导致神经网络崩溃。