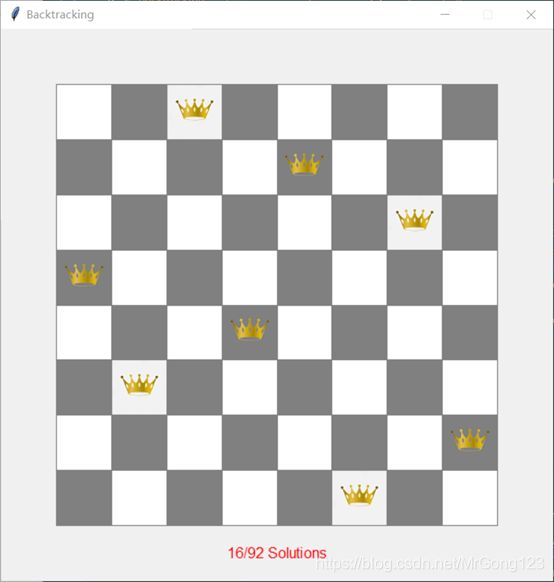
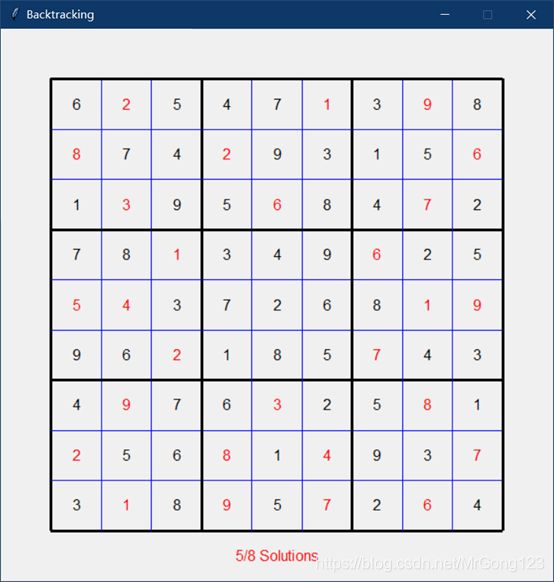
约束满足解决8皇后与数独

约束满足求解8皇后与数独游戏

一、 算法总结

与前面介绍的基于状态空间的搜索方法相比，CSP可以使用通用策略而不是问题特定的启发式方法来求解复杂问题的原因在于：CSP 将状态进行进一步细分，利用一组变量及其值来表示状态。当每个变量的值满足所有关于变量的约束时，问题就得到了求解。

二、求解 CSP 的通用方法

回溯法：

回溯 (Backtracking，BT) 法是一种直接在解空间中按照深度优先搜索策略执 行搜索的通用型算法，即它是一种求解问题的基本策略。为提高它的搜索效率，避免无效的搜索，通常可以采通常可以采取两种措施 1. 使用约束函数剪去不满足约束条件的子树； 2. 使用限界函数剪去得不到最优解的子树（α-β 博弈树搜索算法中就使用了限界函数）。这里讲的是措施一约束函数与回溯框架的结合。

约束传播：

约束传播指的是，使用约束减少变量的合法或有效的 取值范围，并将这种影响传播到与此变量存在约束关系的其它变量上，从而间接 地压缩了状态空间，提高了求解效率。
简单的说，回溯法针对于于全局，具有完备性，如果问题有解则一定能找到解，但其瓶颈在于效率低。而对于约束传播，主要针对于局部的，能够将状态空间进行压缩，提高效率。两者可以说是在某方面互补，将两者结合能够提高算法的准确率和效率。

###小结：

简单的说，回溯法针对于于全局，具有完备性，如果问题有解则一定能找到解，但其瓶颈在于效率低。而对于约束传播，主要针对于局部的，能够将状态空间进行压缩，提高效率。两者可以说是在某方面互补，将两者结合能够提高算法的准确率和效率。

三、针对八皇后算法伪代码分析：

def Consistent(Xi,vi,Solution):相容性判断
for x,v in Solution:
if Xix or viv or abs((Xi-x)/(vi-v))==1:#同一行或者同一列或 者同一对角线，都不符合。
return False
return True
def Backtracking(Vars,Solution):
x,vs=Vars[0]
for v in vs:对于变量的所有可能取值
if Consistent(x,v,Solution):满足相容性时，进一步进行审查，判断是否是问题的部分解
Solution.append((x,v))
if len(Vars)==1:当该变量为最后一个时
return True说明已经找到了问题的完整解。
else:
VarsC=copy.deepcopy(Vars)将当前状态进行保存，便于返回
VarsC.pop(0)
if Backtracking(VarsC,Solution):判断其余下的变量是否能找到相容性解
return True
else:当该变量满足相容性，但其余下的变量不满足时，该取值并不是问题的不分解，应剔除。
Solution.pop()
return False

四、算法源码

八皇后

"""
Created on Sun Aug  9 21:56:44 2020

@author: duxiaoqin
Functions:
    (1)Sudoku class;
"""
import copy
from time import *
from graphics import *
from board import *
from boarddraw import *

def Consistent(Xi, vi, Solution):
    for Xj, vj in Solution:
        if Xi == Xj or vi == vj or abs(Xi - Xj) == abs(vi - vj):
            return False
    return True

def Backtracking(Vars, Solution, Solutions):
    Xi, Vi = Vars[0]
    for vi in Vi:
        if Consistent(Xi, vi, Solution):
            Solution.append((Xi, vi))
            if len(Vars) == 1:
                Solutions.append(copy.deepcopy(Solution))
            else:
                VarsC = copy.deepcopy(Vars)
                VarsC.pop(0)
                Backtracking(VarsC, Solution, Solutions)
            Solution.pop()

def main():
    win = GraphWin('Backtracking', 600, 600, autoflush = False)
    board = Board(8)

    Vars = []
    for row in range(board.height):
        Vars.append((row, list(range(board.width))))
    Solutions = []
    Solution = []
    Backtracking(Vars, Solution, Solutions)
    
    boarddraw = BoardDraw(win, board, 'Queen8-1.png', 'Queen8-2.png')

    text = Text(Point(board.width/2+1, 0.5), '')
    text.setTextColor('red')
    text.draw(win)

    for index, Solution in enumerate(Solutions):
        text.setText('{}/{} Solutions'.format(index+1, len(Solutions)))
        board.board.clear(Board.EMPTY)
        for Xi, vi in Solution:
            board[Xi, vi] = Board.OCCUPIED
        boarddraw.draw(board)
        time.sleep(0.25)
        if win.checkKey() == 'Escape':
            win.close()
            exit()
    time.sleep(1.0)
    win.close()
    
if __name__ == '__main__':
    main()

数独：

"""
Created on Sun Aug  9 21:56:44 2020

@author: duxiaoqin
Functions:
    (1)Sudoku class;
"""
from myarray2d import Array2D

class Sudoku:
    EMPTY = 0
    def __init__(self, size):
        self.sudoku = Array2D(size, size)
        self.sudoku.clear(Sudoku.EMPTY)
        self.size = size
            
    def __getitem__(self, ndxTuple):
        return self.sudoku.__getitem__(ndxTuple)
    
    def __setitem__(self, ndxTuple, value):
        self.sudoku.__setitem__(ndxTuple, value)
        
    def print(self):
        for row in range(self.size):
            for col in range(self.size):
                if self.sudoku[row, col] == Sudoku.EMPTY:
                    print('-', end=' ')
                else:
                    print(self.sudoku[row, col], end=' ')
            print()
            
def main():
    sudoku = Sudoku(9)
    sudoku.print()
    
if __name__ == '__main__':
    main()

这是算法实现代码，要想跑起来还需要其他类的支持详情见链接：
武汉纺织大学杜老师的github

五、算法总结

约束满足与前面所讲搜索算法问题相比较，可以认为是识别问题，对于csp来说，重要的不是路径而是特定的状态。其最突出的就是CSP 将状态进行进一步细分，利用一组变量及其值来表示状态。而这样做的优点在于CSP可以使用通用策略，来替代状态空间搜索中特定的启发式方法来求解复杂问题。

引用：

武汉纺织大学杜老师的github
此文章在学完杜小勤的课程后所写，文章中部分内容是借鉴杜老师。