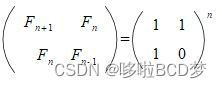具体实例的时间复杂度分析

一.快速排序

1.最坏情况时间复杂度：W(n)=W(n-1)+n-1,W(1)=0

即首元素将剩余元素划分为两个序列，其中一个序列为空，迭代计算得出W(n)=n(n-1)/2。

2.最好情况时间复杂度：W(n)=2W(n/2)+n-1,W(1)=0

运用主定理b=2,a=2,与n-1同阶,则W(n)=Θ(nlogn)

3.均衡划分情况的时间复杂度：W(n)=W(n/9)+W(8n/9)+n-1,W(1)=0

用递归树求解，树的深度较深的一端为W(8n/9)端，由于log函数阶与底数无关，那么深度就是logn

量级，每一层递归树节点的和最大为n-1，那么W(n)=Θ(nlogn)

4.平均情况的时间复杂度

将所有均衡划分的情况与最坏情况的时间按照等概率取平均

W(n)

=((W(1)+W(n-1))+n-1+(W(2)+W(n-2))+n-1+...(W(n-1)+W(1))+n-1)/n

=2(W(1)+W(2)+..W(n-1))/n+n-1

采用两边同乘以n然后错位相减得出递推公式的方法可以得出W(n)=Θ(nlogn)

二.幂乘算法

算某一个数的n次方可以将原问题化为子问题，子问题为算出一半次幂的结果，n为偶数时，一半次

幂的平方为原结果,n为奇数时，一半次幂平方再乘以n为原结果。

1.时间复杂度分析

W(n)=W(n/2)+O(1),W(1)=0

运用主定理，b=2,a=1,W(n)=Θ(logn)

2.运用于计算斐波那契数列

斐波那契数列：F(0)=0,F(1)=1,F(n+2)=F(n+1)+F(n),n>=0

矩阵表示：

代码计算：

#include 
#include 
#include 
#define OVERFLOW -2
#define OK 1
#define ERROR 0
typedef int Status;
//求菲波那切数列第n项
typedef int* Array;
//返回在压缩矩阵中的位置
int ElemPos(int row, int col)
{
	int max, min;
	if (row >= col)
	{
		max = row;
		min = col;
	}
	else
	{
		max = col;
		min = row;
	}
	int k = max * (max - 1) / 2 + min - 1;
	return k;
}
//二维矩阵相乘(这个例子中两个相乘矩阵可以交换，即AB=BA，结果矩阵为对称阵，采用压缩方式存于数组C
//中)
void MultiArray_twodi(Array A, Array B, Array* C)
{
	//采用一般压缩矩阵相乘的算法的来编程，过程繁琐，复杂度为矩阵阶的三次方
	*C = (int*)malloc(sizeof(int) * 3);
	if (!*C) exit(OVERFLOW);
	int buf[2];
	for (int arow = 1; arow <= 2; arow++)
	{
		for (int i = 0; i <= 1; i++)
			buf[i] = 0;
		for (int acol = 1; acol <= 2; acol++)
		{
			int k1 = ElemPos(arow, acol);
			for (int bcol = 1; bcol <= 2; bcol++)
			{
				int k2 = ElemPos(acol, bcol);
				buf[bcol - 1] += A[k1] * B[k2];
			}
		}
		for (int acol = 1; acol <= arow; acol++)
		{
			int k = ElemPos(arow, acol);
			(*C)[k] = buf[acol - 1];
		}
	}
}
Array Fibonacci(int n)
{
	if (n == 1)
	{
		Array A = (int*)malloc(sizeof(int) * 3);
		if (!A) exit(OVERFLOW);
		//一维数组存储矩阵下三角
		A[0] = 1;
		A[1] = 1;
		A[2] = 0;
		return A;
	}
	else
	{
		Array A = Fibonacci((int)floor((double)n / 2));
		Array C;
		MultiArray_twodi(A, A, &C);
		if (n % 2 == 1)
		{
			Array B = (int*)malloc(sizeof(int) * 3);
			if (!B) exit(OVERFLOW);
			//一维数组存储矩阵下三角
			B[0] = 1;
			B[1] = 1;
			B[2] = 0;
			MultiArray_twodi(C, B, &A);
			free(B);
			free(C);
			return A;
		}
		else
		{
			free(A);
			return C;
		}
	}
}
int main()
{
	Array A;
	printf("请输入要输出数列的第几号元素\n");
	int m;
	scanf("%d", &m);
	A = Fibonacci(m);
	printf("第%d号元素为：%d", m, A[1]);
	return 0;
}

 结果：