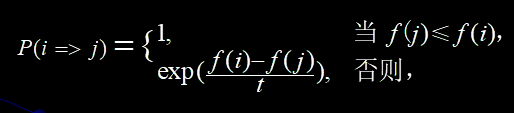用SA算法求解旅行商问题

以下是用模拟退火算法（SA）解决旅行商问题的实验报告

1.问题描述

旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[dij]，其中dij表示城市i到城市j的距离，i，j=1，2 … n，则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。

 

2.算法设计

旅行商问题是一个十分经典的NP难度问题，如果想找到真正的唯一最优的解复杂度是O(N!)的，所以求解这一类问题的策略就是找一个相对最优的解，也就是最优化问题。模拟退火算法就是一种启发式的组合优算法，通过不断迭代来寻找最优解。

旅行商问题最终是要找到一个循环路径，并且使得该路径最短。所以这里我们初始化一条循环路径，然后利用变换法产生新的路径，如果这条路径的长度小于当前路径侧用该路径取代当前路径，否则利用Metropolis准则判断是否接受新的路径。上述过程每次迭代Mapkob链长次，然后利用衰减函数降低温度继续迭代，直到在某一次迭代中循环路径不在变化。

算法流程图如下图所示。

其中

（1）Metropolis准则接受算法为：

 

确定是否接受从当前解 i 到 新解 j 的转移 。式中 t ∈ R+ 表示控制参数。

（2）温度衰减函数为：α(t)=0.9 * t

（3）产生新路径的变换法

         1.随机选择循环路径中的两个城市序号然后交换

         2.随机选择循环路径中的两个城市，然后把这两个城市之间的城市进行逆序

 

 

 

3.程序流程

1.初始化各个城市的坐标信息

2.生成初始路径Li并计算, 并且计算目标函数即路径长度f(Li)

3.利用变换法产生新路径Li+1, 并计算新的f(Li+1)

4.判断f(Li)与f(Li+1)的大小，如果后者小侧接受新的路径，否则用Metropolis准则判断是否接受新的路径

5.判断是否达到迭代次数，如果达到转到步骤6，否则转到步骤3

6.判断是否满足算法终止条件，没有达到的话用衰减函数降低温度然后转到步骤3，达到的话转到步骤7

7.输出找到的最后路径以及路径长度

 

4.核心代码

import math
import time
import random
import copy

class Path(object):
    def __init__(self, map, path, nums):
        self.map = map
        self.path = path
        self.nums = nums
        self.len = self.calLen()

    def calLen(self):
        self.len = 0
        for i in range(self.nums-1):
            self.len += self.Caldis(self.map[self.path[i]-1], self.map[self.path[i+1]-1])
        self.len += self.Caldis(self.map[self.path[nums-1]-1], self.map[self.path[0]-1])
        return self.len

    def Caldis(self, c1 ,c2):
        dis = 0
        for i, j in zip(c1, c2):
            dis += pow(math.fabs(i-j), 2)

        return math.sqrt(dis)

class SA(object):
    def __init__(self, L, T, solution, r=0.9):
        self.L = L
        self.T = T
        self.solution = solution
        self.r = 0.9

    def generate1(self): #随机选择循环路径中的两个城市序号然后交换
        nums = self.solution.nums
        c1, c2 = 0, 0
        while c1 == c2:
            c1 = random.randint(0, nums-1)
            c2 = random.randint(0, nums-1)
        new_path = copy.deepcopy(self.solution.path)
        new_path[c1], new_path[c2] = new_path[c2], new_path[c1]
        new_solution = Path(self.solution.map, new_path, nums)

        return new_solution

    def generate2(self): #随机选择循环路径中的两个城市，然后把这两个城市之间的城市进行逆序
        nums = self.solution.nums
        c1, c2 = 0, 0
        while c1 == c2:
            c1 = random.randint(0, nums - 1)
            c2 = random.randint(0, nums - 1)
        new_path = copy.deepcopy(self.solution.path)
        begin = min(c1, c2)
        end = max(c1, c2)
        while begin <= end:
            new_path[begin], new_path[end] = new_path[end], new_path[begin]
            begin += 1
            end -= 1
        new_solution = Path(self.solution.map, new_path, nums)

        return new_solution

    def generate(self): #产生新个体
        rate = random.random()
        if rate > 0.5:
            return self.generate1()
        else:
            return self.generate2()

    def accept(self, new_solution): #判断是否接收
        rate = random.random()
        r = math.exp((self.solution.len-new_solution.len)/self.T)
        if  r >= rate and r < 1:
            return True
        else:
            return False

    def process(self):
        flag = 0
        while(flag<2):
            bchange = 0
            for i in range(self.L):
                new_solution = self.generate() #产生新路径
                if new_solution.len < self.solution.len: #新的路径长度小直接接收
                    self.solution = copy.deepcopy(new_solution)
                    bchange += 1
                elif self.accept(new_solution): #否则按照Metropolis进行接收
                    self.solution = copy.deepcopy(new_solution)
                    bchange += 1

            self.T = self.r * self.T
            if bchange == 0:
                flag += 1
            else:
                flag = 0





ii = 0
L = 20000  # 设置Mapkob链长
T = 100  # 设置初始温度
r = 0.9  # 控制参数
while ii <= 3:
    #读取数据 第一行为城市的个数n，随后n行为每个城市的坐标(x,y)
    with open('path.txt', 'r') as f:
        lines = f.readlines()

    nums = int(lines[0].replace('\n', ""))
    map = []
    for i in range(1, len(lines)):
        city = [j for j in lines[i].replace('\n', "").split(' ')]
        while '' in city:
            city.remove('')
        city = [float(j) for j in city]
        map.append(city[1::])

    init_path = [i for i in range(1, nums+1)]
    path = Path(map, init_path, nums)
    sa = SA(L, T, path, r)
    t_b = time.time()
    sa.process()
    t_e = time.time()
    print("nums_city:{}, r:{}, path:{}, len:{}, time:{}".format(nums, r, sa.solution.path, sa.solution.len, (t_e-t_b)))
    ii += 1
    r = r-0.1

 

6.结论

旅行商问题属于NP难问题，无法在线性的复杂度中求解。利用模拟退火算法这种启发式的算法能够有效的找到相对的最优解，而且大大缩短了运行时间。不过模拟退火算法也存在偶然性，即可能陷入到某个局部最优值中，这个时候温度的初始值以及温度衰减函数的设置就显得尤为重要。这些都要根据实际情况再进行实际的实验以得到最好的结果

 

源码以及测试数据集：https://download.csdn.net/download/breeze_blows/11968387