聚类分析&主成分分析

样本的相似性度量

一、聚类分析

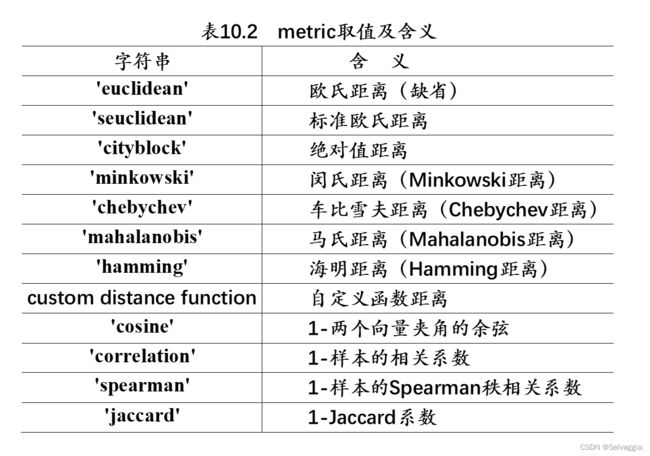
pdist

Y=pdist(X,metric)

linkage

cluster

demo1

clc,clear
a=[1,0;1,1;3,2;4,3;2,5];
z=linkage(a, 'single', 'cityblock')  %产生等级聚类树
dendrogram(z) %画聚类图
T=cluster(z,'maxclust',3)  %把对象划分成3类
for i=1:3
    tm=find(T==i);  %求第i类的对象
    fprintf('第%d类的有%s\n',i,int2str(tm')); %显示分类结果
end

分成3类，矩阵z的含义不必太纠结，T矩阵代表原先的指标所属的类，通过循环找出每一类包含的指标

z =

     1     2     1
     3     4     2
     6     7     3
     5     8     4


T =

     1
     1
     2
     2
     3

第1类的有1  2
第2类的有3  4
第3类的有5

demo2

linkage变量相当于pdist生成的行向量 （ 1，m*(m-1)/2 ）

clc, clear, close all
a=readmatrix('data10_2.txt');  a(isnan(a))=0;   
d=1-abs(a); %进行数据变换,把相关系数转化为距离
d=tril(d)  %提出d矩阵的下三角部分
b=nonzeros(d)%去掉d中的零元素，非零元素按列排列
b=b';  %化成行向量
z=linkage(b,'complete'); %按最长距离法聚类  
y=cluster(z,'maxclust',2)   %把变量划分成两类
ind1=find(y==1);ind1=ind1'  %显示第一类对应的变量标号
ind2=find(y==2);ind2=ind2'  %显示第二类对应的变量标号
h=dendrogram(z); %画聚类图
set(h,'Color','k','LineWidth',1.3)  %把聚类图线的颜色改成黑色，线宽加粗

demo3

clc, clear, close all
a=readmatrix('anli10_1.txt');
b=zscore(a); %数据标准化
r=corrcoef(b) %计算相关系数矩阵,这里只是通过相关系数初步大致观察分析并不使用数据
%d=tril(1-r); d=nonzeros(d)'; %另外一种计算距离方法
z=linkage(b','average','correlation');  %按类平均法聚类
h=dendrogram(z);  %画聚类图
set(h,'Color','k','LineWidth',1.3)  %把聚类图线的颜色改成黑色，线宽加粗
T=cluster(z,'maxclust',6)  %把变量划分成6类
for i=1:6
    tm=find(T==i);  %求第i类的对象
    fprintf('第%d类的有%s\n',i,int2str(tm')); %显示分类结果
end

二、主成分分析

clc,clear
a=readmatrix('data10_5.txt'); [m,n]=size(a);
x0=a(:,[1:n-1]); y0=a(:,n); 
hg1=[ones(m,1),x0]\y0;   %计算普通最小二乘法回归系数
hg1=hg1' %变成行向量显示回归系数,其中第1个分量是常数项，其它按x1,...,xn排序
fprintf('y=%f',hg1(1)); %开始显示普通最小二乘法回归结果
for i=2:n
    if hg1(i)>0  
       fprintf('+%f*x%d',hg1(i),i-1);
    else
       fprintf('%f*x%d',hg1(i),i-1)
    end
end
fprintf('\n')  

r=corrcoef(x0)  %计算相关系数矩阵
xd=zscore(x0)  %对设计矩阵进行标准化处理
yd=zscore(y0)  %对y0进行标准化处理
[vec1,lamda,rate]=pcacov(r) %vec1为r的特征向量，lamda为r的特征值，rate为各个主成分的贡献率

f=repmat(sign(sum(vec1)),size(vec1,1),1) %构造与vec1同维数的元素为±1的矩阵
vec2=vec1.*f %修改特征向量的正负号，使得特征向量的所有分量和为正
contr=cumsum(rate) %计算累积贡献率，第i个分量表示前i个主成分的贡献率

df=xd*vec2  %计算所有主成分的得分
% num=input('请选项主成分的个数:') %通过累积贡献率交互式选择主成分的个数
num=3;
% df1=xd*vec2(:,1:num)  %计算各个主成分的得分
hg21=df(:,[1:num])\yd  %主成分变量的回归系数,这里由于数据标准化，回归方程的常数项为0
hg22=vec2(:,1:num)*hg21  %标准化变量的回归方程系数
hg23=[mean(y0)-std(y0)*mean(x0)./std(x0)*hg22, std(y0)*hg22'./std(x0)]  %计算原始变量回归方程的系数
fprintf('y=%f',hg23(1)); %开始显示主成分回归结果
for i=2:n
    if hg23(i)>0
        fprintf('+%f*x%d',hg23(i),i-1);
    else
        fprintf('%f*x%d',hg23(i),i-1);
    end
end
fprintf('\n')
%下面计算两种回归分析的剩余标准差
rmse1=sqrt(sum((hg1(1)+x0*hg1(2:end)'-y0).^2)/(m-n))   %拟合了n个参数
rmse2=sqrt(sum((hg23(1)+x0*hg23(2:end)'-y0).^2)/(m-num)) %拟合了num个参数

% AA=[1,-2;3,4];
% sign(AA)

其中，hg21是主成分变量回归系数、hg22是标准化X的回归系数(没有常数项)，hg23是原始X的回归系数（第一个是常数项）