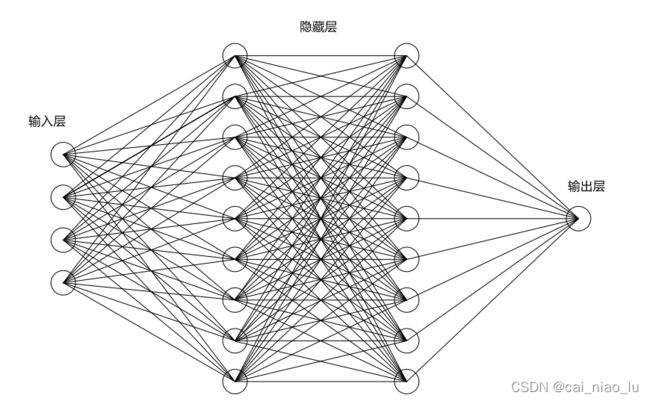
机器学习算法模型之神经网络

1. 神经网络是一个嵌套的过程，注意不是一个回归的过程。要搞清楚神经网络，主要是搞清楚神经网络是如何工作的。
    1. 权重w的求解
    2. 激活函数的选择
    3. 隐藏层的层数和每一层对应神经元的个数
    综合以上三个过程的结束，我们的神经网络的框架就算是搭建完成了。
2. 神经网络在sklearn中的API
    1. 分类器
        sklearn.neural_network.MLPClassifier(hidden_layer_sizes=(100,), activation='relu', *, solver='adam', alpha=0.0001, batch_size='auto', learning_rate='constant', learning_rate_init=0.001, power_t=0.5, max_iter=200, shuffle=True, random_state=None, tol=0.0001, verbose=False, warm_start=False, momentum=0.9, nesterovs_momentum=True, early_stopping=False, validation_fraction=0.1, beta_1=0.9, beta_2=0.999, epsilon=1e-08, n_iter_no_change=10, max_fun=15000)
            1. hidden_layer_sizes:传入一个元组， 例如（50，50），这表示第一层隐藏层和第二层隐藏层都有50个神经元。
            2. activation: 激活函数，{'identity','logistic','tanh','relu'}，默认是relu
            3. solver: 权重优化器，{'lbfgs','sgd','adam'}, 默认是adam
                lbfgs：quasi-Newton方法的优化器
                sgd：随机梯度下降
                adam：Kingma， Diederik和Jimmy Ba提出的机遇随机梯度的优化器
                注意，默认solver的adam在相对较大的数据集上效果较好（几千个或者几万个），对小数据集来讲，lbfgs收敛更快，效果更好。
            4. alpha: float，正则惩罚项
            5. batch_size: int， 默认auto， 随即优化的minibatches的大小
            6. learning_rate: 学习率，用于权重的更新，只有当solver为'sdg'时使用，{'constant','invscaling','adaptive'}，默认是'constant'
            7.shuffle: bool, 是否对每次嵌套时对样本进行清洗, 在solver为sgd和adam时候可以选用
            8.learning_rate_int: 默认0.001，初始学习率，solver随机梯度下降或者adam时候使用。
            
    2. 回归器
        sklearn.neural_network.MLPRegressor()
        回归器和分类器的参数相同
    3. API的属性说明：
        coefs_: 包含w的矩阵，可以通过迭代获得每一层神经网络的权重矩阵
        classes_: 每个输出的类标签
        loss_: 损失函数计算出来的当前损失值
        coefs_: 列表中的第i个元素表示i层的权重矩阵
        intercepts_: 列表中第i个元素代表i+1层的偏差向量
        n_iter_ ：迭代次数，注意这里的迭代次数是权重的迭代次数。
        n_layers_: 层数
        n_outputs_: 输出的个数
        out_activation_: 输出激活函数的名称
3. 神经网络使用的范围：
    数据量非常大的场景来进行。
4. 神经网络的优缺点：
    优点：预测非常的准确
    缺点：由于其过程非常复杂，因此不好说明。不容易表达出来。

 

由于回归器和分类器的参数相同，这里我们只仅仅对回归器进行代码演示

数据如下：我们的特征数据为‘拥堵延时指数、高延时运行时间占比、拥堵路段里程比、平均车速’，我们的目标集为‘交通健康指数’

城市名称	城市代码	交通健康指数	交通延时指数	高延时运行时间占比	拥堵路段里程比	平均车速
中山市	442000	0.743635484	1.595913978	53.13612903	1.679193548	28.26258065
临沂市	371300	0.759006452	1.568817204	48.29747312	1.571397849	29.85091398
兰州市	620100	0.740470968	1.508978495	37.99290323	1.838548387	27.91311828
南宁市	450100	0.757883871	1.478924731	30.01784946	1.26811828	28.51892473
南昌市	360100	0.760412903	1.499193548	36.55903226	1.618172043	30.64521505
南通市	320600	0.78006129	1.373225806	17.29397849	0.641290323	36.31129032
厦门市	350200	0.765535484	1.486290323	35.03580645	1.602096774	33.4133871
台州市	331000	0.7707	1.489193548	38.17193548	1.016774194	30.18037634
合肥市	340100	0.757322581	1.496451613	39.33693548	1.406505376	29.20225806
哈尔滨市	230100	0.753622581	1.565913978	48.02849462	1.943172043	28.65483871
嘉兴市	330400	0.778045161	1.384086022	21.68435484	0.524193548	30.47215054
大连市	210200	0.740941935	1.621451613	59.94623656	1.829623656	29.05290323
太原市	140100	0.751303226	1.55155914	39.24698925	2.113602151	31.8844086
常州市	320400	0.765151613	1.435107527	30.19688172	0.69311828	31.96709677
徐州市	320300	0.755609677	1.477150538	38.26166667	1.288817204	29.62478495
惠州市	441300	0.744277419	1.552365591	47.93887097	1.660053763	28.59102151
无锡市	320200	0.753158065	1.419032258	30.645	1.255806452	33.03451613
昆明市	530100	0.745764516	1.540537634	43.90688172	1.972311828	28.21462366
泉州市	350500	0.785393548	1.388602151	24.01424731	0.840483871	33.10064516
济南市	370100	0.744958065	1.68483871	60.75241935	2.133709677	28.18612903
温州市	330300	0.750845161	1.514569892	46.59478495	1.290322581	25.28204301
潍坊市	370700	0.778345161	1.538602151	49.19354839	0.705322581	28.54231183
烟台市	370600	0.767974194	1.528817204	47.67021505	0.73672043	30.69768817
珠海市	440400	0.753825806	1.534086022	42.47311828	1.471774194	34.25344086
石家庄市	130100	0.757196774	1.512365591	38.79924731	1.51311828	31.24752688
福州市	350100	0.750977419	1.59655914	50.62741935	1.679892473	28.88032258
绍兴市	330600	0.760645161	1.492311828	40.2327957	1.067311828	27.47043011
贵阳市	520100	0.736306452	1.561021505	43.6377957	3.067634409	31.57268817
金华市	330700	0.769812903	1.368602151	16.93553763	0.632473118	29.11575269
长春市	220100	0.737064516	1.667473118	65.68096774	2.363655914	27.95241935

创建的神经网络结果如图所示：

代码演示如下：

from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
import pandas as pd


# 数据集获取
path = "E:\Desktop\二线城市交通大数据(整理版本).xlsx"
data = pd.read_excel(path)
x = data.iloc[:, 3:]
y = data['交通健康指数']

# 拆分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22, test_size=0.2)

# 神经网络评估器的流程
# 实例化预估器
estimator = MLPRegressor(hidden_layer_sizes=(9, 9), activation='relu', solver='lbfgs',max_iter=10000)

# 模型训练
estimator.fit(x_train, y_train)

# 模型结果
print('权重为:\n', estimator.coefs_)
print('偏置为:\n', estimator.intercepts_)
print('迭代次数:\n', estimator.max_iter)

# 模型评估
print(mean_squared_error(y_true=y_test, y_pred=estimator.predict(x_test)))

# 画图分析
plt.plot([i for i in range(len(y_test))], y_test, label='true')
plt.plot([i for i in range(len(y_test))], estimator.predict(x_test), label='predict')
plt.legend()
plt.show()

 输出结果为：

权重为:
 [array([[ 0.42577168,  0.17666234,  0.19003966,  0.26250721,  0.3317495 ,
         0.08508971, -0.22039682, -0.35895583, -0.13872385],
       [-0.37564312, -0.59776873,  0.46398324, -0.20914132, -0.48539331,
         0.33594829,  0.22823493,  0.0282387 , -0.49696628],
       [-0.29733362,  0.1314713 ,  0.04251641, -0.53688462, -0.33659041,
         0.49136256,  0.32953032,  0.39113453, -0.26674058],
       [ 0.12170368, -0.3033268 , -0.46451011, -0.09668492,  0.23758192,
        -0.31235258, -0.58519066, -0.01642481,  0.07302027]]), array([[-3.87153101e-01, -4.41334063e-01,  2.05860764e-01,
        -5.71204328e-01,  2.86162288e-01, -3.47884587e-01,
         2.58576352e-01, -8.90988416e-02,  4.77097423e-01],
       [-8.41104197e-02,  4.91815922e-01, -4.45543029e-01,
         1.76201627e-01,  2.47454291e-01, -1.42124659e-01,
         3.05051279e-02, -2.04327463e-01, -1.22892624e-02],
       [ 8.52969740e-02,  1.81415220e-01,  4.49311909e-01,
        -3.33872078e-01,  1.58314641e-01, -3.56945623e-01,
         2.72664354e-01, -3.20190743e-02,  2.95226558e-01],
       [ 5.36893944e-01, -5.14863968e-01, -1.69998148e-01,
         5.73832139e-01,  3.27003319e-01,  1.12153740e-01,
         3.53775468e-01,  4.96910910e-02, -2.06986749e-01],
       [-2.51883778e-01,  1.64562422e-01,  6.20866569e-02,
         5.62702793e-01, -3.10472029e-01, -1.55396850e-01,
        -1.18747530e-01,  5.58967054e-01,  3.12433716e-01],
       [ 2.10134725e-01,  8.63839437e-02, -2.26089459e-01,
        -4.34510907e-01,  2.88601412e-01, -3.81954622e-01,
         3.49619056e-01,  4.09807358e-01,  4.69517473e-01],
       [-1.54442824e-04,  3.05257781e-01,  5.63687971e-01,
        -5.52803397e-01, -3.22323538e-01,  2.10270416e-01,
        -2.06400717e-01,  4.73932003e-01, -4.94360991e-01],
       [ 3.72320528e-01,  1.05820561e-01, -5.67804032e-01,
        -4.01005888e-01, -3.53290114e-02,  2.46396546e-01,
        -7.04286272e-02,  4.24332860e-01,  1.40415718e-01],
       [-2.42658334e-02, -4.06160053e-01, -4.42680874e-02,
        -3.98431087e-02,  2.70100216e-01, -3.00897123e-01,
        -2.83378521e-01, -1.03931077e-01,  2.49463069e-01]]), array([[-0.29808742],
       [-0.08643562],
       [-0.35921175],
       [-0.75997322],
       [ 0.32831232],
       [ 0.30329984],
       [ 0.50290044],
       [-0.35763353],
       [-0.14015589]])]
偏置为:
 [array([ 0.23508308, -0.30508132, -0.42374356,  0.08324226, -0.46454786,
       -0.31669358,  0.20434223, -0.43277333,  0.27982283]), array([ 0.03710788, -0.17710693,  0.19630572, -0.32625699, -0.45168697,
        0.08850363,  0.44465056,  0.0520729 , -0.3625317 ]), array([0.62700466])]
迭代次数:
 10000
均方误差
 3.710511288209076e-05