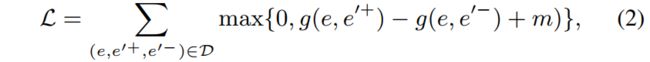论文简读-BERT-INT-《 A BERT-based Interaction Model For Knowledge Graph Alignment》
论文简读-BERT-INT-《 A BERT-based Interaction Model For Knowledge Graph Alignment》
会议：IJCAI 2020
源码：https://github.com/kosugi11037/bert-int
1. 动机
(1). 在实体对齐任务中，知识图谱的side information（边缘信息：包括名称、描述和属性）比structural information（结构信息：知识图谱的图结构）更有用。
(2). 由于知识图谱的异构性，对齐的实体往往不具有相同的邻域，使得知识图谱的结构信息难以利用，从而对齐的准确率较低。
2. 方法
\,\,\,\,\,\,\,\,\,\, 本文提出的方法仅仅使用知识图谱的边缘信息，其做法并非聚集邻居节点，而是计算邻居节点之间的相互作用（邻居节点name/description信息的相互作用），这种相互作用能够捕获邻居节点之间细粒度的匹配。相似地，还计算了节点本身属性的相互作用。
2.1. 符号定义
2.2. BERT-INT 模型
\,\,\,\,\,\,\,\,\,\, 模型的整体框架如图2所示，BERT-INT采用BERT模型作为基础单元处理实体的边缘信息。本文所提出的交互模型包含三个部分：①实体本身的name/description交互；②邻居视图name/description交互③实体本身的属性视图交互。三种交互的结果向量进行拼接操作形成交互结果向量，将该向量传入多层感知机MLP得到实体对的相似度。
2.2.1. BERT-Unit
\,\,\,\,\,\,\,\,\,\, 如图2所示，首先利用与训练的BERT模型对实体的name/description进行计算（优先采用description，当其缺失时，用name代替），取CLS标签对应值，然后使用MLP进行映射，得到的结果作为该实体的向量表示：
基于该向量表示和边缘损失来微调BERT模型参数，公式如下：
其中 g ( . ) g(.) g(.)表示向量 C ( e ) C(e) C(e)和 C ( e ′ ) C(e') C(e′)曼哈顿距离函数， m m m为边缘超参数。负样本的采样方法同BootEA中提出的方法。由于计算资源不足，Bert单元将采用以上方法微调，在后续的交互过程中，bert模型参数将会被固定。
2.2.2. name/description交互
\,\,\,\,\,\,\,\,\,\, 给定 K G KG KG和 K G ′ KG' KG′中的两个实体 e e e和 e ′ e' e′，使用上述BERT单元计算实体 e e e和 e ′ 的 e'的 e′的name/description向量表示 C ( e ) C(e) C(e)和 C ( e ′ ) C(e') C(e′)，然后计算 C ( e ) C(e) C(e)和 C ( e ′ ) C(e') C(e′)的余弦相似度，计算结果即为name/description交互。
2.2.3. 邻居视图交互
\,\,\,\,\,\,\,\,\,\, 给定 K G KG KG和 K G ′ KG' KG′中的两个实体 e e e和 e ′ e' e′，首先根据公式(1)计算 e e e和 e ′ e' e′的邻居节点的name/description的向量表示，得到两个向量集合 { C ( e i ) } i = 1 ∣ N ( e ) ∣ \{C(e_i)\}_{i=1}^{|N(e)|} {C(ei)}i=1∣N(e)∣和 { C ( e j ′ ) } j = 1 ∣ N ( e ′ ) ∣ \{C(e'_j)\}_{j=1}^{|N(e')|} {C(ej′)}j=1∣N(e′)∣，然后使用余弦相似度计算这两个向量集合的相似度矩阵 S S S，其元素计算公式为 s i j = C ( e i ) ⋅ C ( e j ′ ) ∣ ∣ C ( e i ) ∣ ∣ ⋅ ∣ ∣ C ( e j ′ ) ∣ ∣ s_{ij}=\frac{C(e_i)\cdot C(e'_j)}{||C(e_i)||\cdot||C(e'_j)||} sij=∣∣C(ei)∣∣⋅∣∣C(ej′)∣∣C(ei)⋅C(ej′)，最后使用双重聚合方法对 S S S进行计算，得到邻居视图交互向量。
\,\,\,\,\,\,\,\,\,\, 所谓双重聚合方法，就是分别从矩阵 S S S的行方向和列方向进行聚合，最终将两个方向的聚合结果向量进行拼接。其中行聚合步骤如下：
- 1). 对每行进行最大池化运算。对于第 i i i行向量 S i = { S i 0 , S i 1 , . . . , S i n } S_i=\{S_{i0}, S_{i1}, ...,S_{in} \} Si={Si0,Si1,...,Sin}，取其中的最大值 S i m a x S_i^{max} Simax。这么做的理由是：由于知识图谱的异构性，两个对齐实体 e e e和 e ′ e' e′的邻居实体并非完全相同，我们只关心 e e e的某个邻居实体与 e ′ e' e′的邻居实体中最相似的那个实体的相似度。
- 2). 使用高斯核函数对 S i m a x S_i^{max} Simax进行一对多映射，得到多个映射值，组成向量 K r ( S i ) K^r(S_i) Kr(Si)。作者给出的解释为一对多的映射可以提高
- 3). 最后在列方向上对 K r ( S ) K^r(S) Kr(S)矩阵求对数平均值，得到长度为 L L L的向量。
\,\,\,\,\,\,\,\,\,\, 行聚合的所有公式如公式(3)所示，列聚合步骤与其相似。
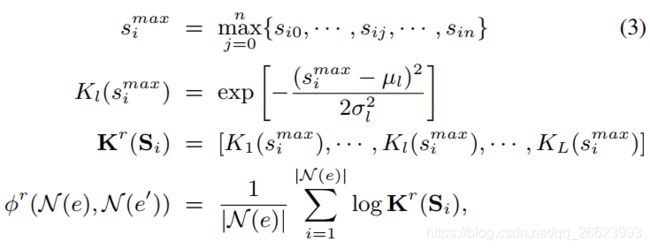
其中 n n n表示最大邻居数， L L L表示高斯核个数， r r r指示行聚合。
\,\,\,\,\,\,\,\,\,\, 将行聚合和列聚合的结果进行拼接，得到邻居视图交互相似度向量 ϕ ( N ( e ) , N ( e ′ ) ) \phi(N(e),N(e')) ϕ(N(e),N(e′))：
其中 ⨁ \bigoplus ⨁表示拼接运算。
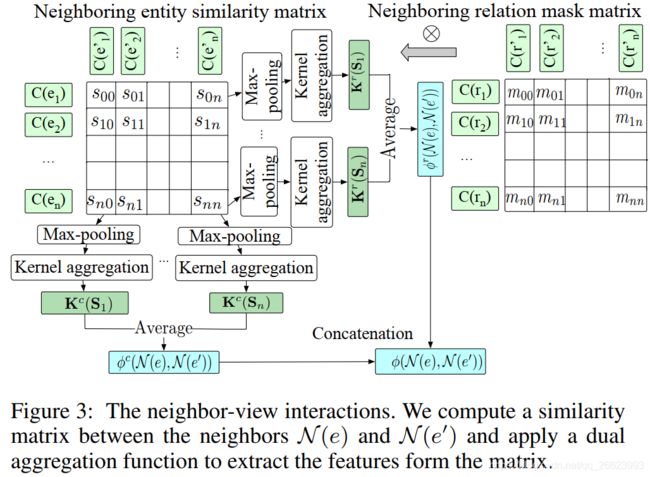
\,\,\,\,\,\,\,\,\,\, 对于对齐的实体 e e e与 e ′ e' e′，他们的某个邻居三元组分别为 ( e , r i , e i ) (e,r_i,e_i) (e,ri,ei)和 ( e ′ , r j ′ , e j ′ ) (e',r'_j,e'_j) (e′,rj′,ej′)，如果邻居实体 e i e_i ei与邻居实体 e j ′ e'_j ej′相似，则关系 r i r_i ri与关系 r j ′ r'_j rj′在于以上应该也是相似的。基于以上推断，作者不仅利用邻居计算相似度矩阵 S S S，还利用与邻居关系计算掩饰矩阵 M M M，对邻居实体相似度矩阵进行校正，处理步骤如下：
- 1). 首先对关系的头实体集合和尾实体集合分别求 C ( e ) C(e) C(e)向量平均，将求得的两个向量进行拼接操作，得到关系的向量表示。
- 2). 然后，根据实体 e e e、 e ′ e' e′的多个邻居关系向量求得相似度矩阵 M M M。 M i j = s i m ( C ( r i ) , C ( r j ′ ) ) M_{ij}= sim(C(r_i), C(r'_j)) Mij=sim(C(ri),C(rj′))， M i j M_{ij} Mij表示实体 e e e的第 i i i个邻居的关系 r i r_i ri与实体 e ′ e' e′的第 j j j个邻居的关系 r j ′ r'_j rj′的余弦相似度。
- 3). 最后使用 M M M校正 S S S，公式为 S = S ⨂ M S=S\bigotimes M S=S⨂M， 其中 ⨂ \bigotimes ⨂元素间乘法运算。
最终通过关系掩饰矩阵 M M M校正的邻居视图交互示意图如图3所示：
2.2.4. 属性视图交互
\,\,\,\,\,\,\,\,\,\, 实体 e e e和 e ′ e' e′的某个属性三元组分别为 ( e , a i , v i ) (e,a_i,v_i) (e,ai,vi)， ( e ′ , a j ′ , v j ′ ) (e',a'_j,v'_j) (e′,aj′,vj′)，与实体的邻居关系三元组相似，因此属性视图交互可以类比于邻居视图交互，相似度矩阵根据属性值计算： S i j = s i m ( C ( v i ) , C ( v j ′ ) ) S_{ij}=sim(C(v_i),C(v'_j)) Sij=sim(C(vi),C(vj′))，掩饰矩阵根据属性名称计算： M i j = s i m ( C ( a i ) , C ( a j ′ ) ) M_{ij}=sim(C(a_i),C(a'_j)) Mij=sim(C(ai),C(aj′))，其他步骤与邻居视图交互相同，最终得到属性视图交互相似度向量 ϕ ( A ( e ) , A ( e ′ ) ) \phi(A(e),A(e')) ϕ(A(e),A(e′))。
2.2.5. 交互聚合
\,\,\,\,\,\,\,\,\,\, 将①实体本身的name/description交互相似度值、②邻居视图name/description交互相似度向量和③实体本身的属性视图交互相似度向量进行聚合（也就是拼接操作），得到实体对 ( e , e ′ ) (e,e') (e,e′)的相似度向量 ϕ ( e , e ′ ) \phi(e,e') ϕ(e,e′)，然后使用MLP网络计算实体之间的相似度分数 g ( e , e ′ ) g(e,e') g(e,e′)，公式表示如下：
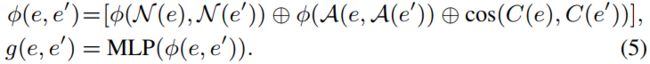
其中 ⨁ \bigoplus ⨁表示拼接运算。最终 ，将 g ( e , e ′ ) g(e,e') g(e,e′)带入到公式(2)边缘损失计算公式中，根据该损失微调公式(5)的MLP网络参数。
2.2.6. 实体对齐
\,\,\,\,\,\,\,\,\,\, 实体对齐过程中，先根据实体的 C ( e ) C(e) C(e)向量计算 k k k个余弦相似度最高的候选对齐实体，然后再使用以上方法分别计算 k k k个候选实体与 e e e间的相似度分数值 g ( e , e ′ ) g(e,e') g(e,e′)，最后对结果进行从大到小排列。
3. 实验
3.1. 数据集和参数设置
\,\,\,\,\,\,\,\,\,\, 数据集采用交叉语言的DBP15K和单语言的DWY100K，衡量指标为 H i t R a t i o @ K ( K = 1 , 10 ) HitRatio@K (K=1,10) HitRatio@K(K=1,10)和 M R R MRR MRR。
| 参数名 | 参数值 |
|---|---|
| CLS长度 | 768 |
| 公式(1)中MLP输出维度 | 300 |
| 公式(5)中MLP的维度 | 11->1 |
| n | 50 |
| 边缘参数m（微调bert时） | 3 |
| 边缘参数m（训练公式(5)中MLP时） | 1 |
| L L L | 20 |
| μ \mu μ | 0.025到0.975，间隔0.05，共20个 |
| σ \sigma σ | 0.1 |
3.2. 实验结果
3.2.1. DBP15K上的结果
3.2.2. DWY100K上的结果
\,\,\,\,\,\,\,\,\,\, 模型CEAFF在HR1指标上达到100%，本文的BERT-INT在DWY100K的两个子数据集上的HR1结果分别为99.2%和99.9%
3.2.3. 消融学习
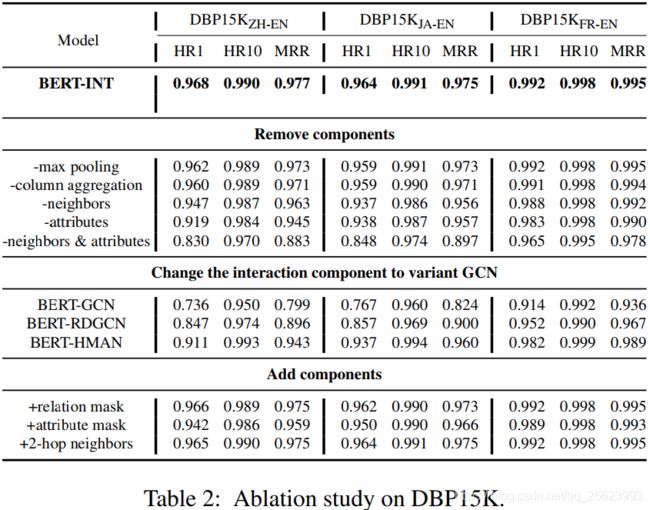
\,\,\,\,\,\,\,\,\,\, 从结果可以看出，最大池化操作、列聚合、邻居视图交互和自身属性交互为高准确率提供了积极作用；使用图网络模型替换多视图交互方法得到的结果不理想；掩饰矩阵对结果没有积极的贡献，甚至有消极作用；多跳邻居视图对结果几乎没有影响。
4. 结论
\,\,\,\,\,\,\,\,\,\, 本文通过构建基于BERT嵌入的邻域和属性之间的交互来解决知识图对齐问题，从而获得邻居和属性的细粒度匹配，与其他模型相比，该模型的性能最好。
文章为阅读随笔，如有错误之处请批评指正，感谢您的阅读！