基于sklearn的线性回归实现房价预测
线性回归介绍
经典的线性回归模型主要用来预测一些存在着线性关系的数据集。回归模型可以理解为:存在一个点集,用一条曲线去拟合它分布的过程。如果拟合曲线是一条直线,则称为线性回归。如果是一条二次曲线,则被称为二次回归。线性回归是回归模型中最简单的一种。 本教程使用PaddlePaddle建立起一个房价预测模型。
在线性回归中:
(1)假设函数是指,用数学的方法描述自变量和因变量之间的关系,它们之间可以是一个线性函数或非线性函数。 在本次线性回顾模型中,我们的假设函数为 Y’= wX+b ,其中,Y’表示模型的预测结果(预测房价),用来和真实的Y区分。模型要学习的参数即:w,b。
(2)损失函数是指,用数学的方法衡量假设函数预测结果与真实值之间的误差。这个差距越小预测越准确,而算法的任务就是使这个差距越来越小。 建立模型后,我们需要给模型一个优化目标,使得学到的参数能够让预测值Y’尽可能地接近真实值Y。这个实值通常用来反映模型误差的大小。不同问题场景下采用不同的损失函数。 对于线性模型来讲,最常用的损失函数就是均方误差(Mean Squared Error, MSE)。
(3)优化算法:神经网络的训练就是调整权重(参数)使得损失函数值尽可能得小,在训练过程中,将损失函数值逐渐收敛,得到一组使得神经网络拟合真实模型的权重(参数)。所以,优化算法的最终目标是找到损失函数的最小值。而这个寻找过程就是不断地微调变量w和b的值,一步一步地试出这个最小值。 常见的优化算法有随机梯度下降法(SGD)、Adam算法等等
准备数据
from sklearn.datasets import load_boston
boston = load_boston()
需要注意的是,在上述代码中,当我们要导入某个方法时,不需要添加方法后面的那对圆括号。变量名 boston 实际上是一个字典类型的对象,我们可以用它的 keys( ) 方法输出它所包含的属性值。
In [2]: boston.keys()
Out[2]:dict_keys(['data', 'target', 'feature_names', 'DESCR', 'filename'])
在 sklearn 框架中,所有内置的数据集(如表 1 所示)都有这 5 个属性值。它们所代表的含义分别如下:
- 首先,data 并不泛指数据,而是特指除标签之外的特征数据,针对波士顿房价数据集,它指的是前面的13个特征;
- 相对而言,target 的本意是“目标”,这里是指标签(label)数据。针对波士顿房价数据集,就是指房价;
- 属性值 feature_names 给出的实际上就是 data 对应的各个特征的名称。对于波士顿房价数据集而言,它指的就是影响房价的 13 个特征的名称;
- 属性值 DESCR 其实是英文单词“description”的简写。顾名思义,它是对当前数据集的详细描述,有点类似于数据集的说明文档。比如,这个数据从哪里来,它有什么特征,每个特征是什么数据类型,如果引用数据集该引用哪些论文,等等;
- 最后一个属性值就是 filename,它说明的是这个数据集的名称,以及在当前计算机中的存储路径。
boston中不仅包括 data 的 13 个特征描述,还包括第 14 个特征,即自住房屋的中位数房价,它作为目标变量(target)—我们使用前面的 13 个特征作为解释变量,建立一个回归模型,对其进行预测。
X = boston.data
y = boston.target
这样就完成了数据集的加载
网络配置
网络搭建:对于线性回归来讲,它就是一个从输入到输出的简单的全连接层。
对于波士顿房价数据集,假设属性和房价之间的关系可以被属性间的线性组合描述。
![]()
from sklearn.linear model import LinearRegression #导入模型
LR = LinearRegression() #生成模型
LR.fit(X_train, y_train) #训练模型
y_pred = LR.predict(X_test) #模型预测
在上述代码中,第 01 行的作用是导入线性回归模型,它是由 sklearn 提供的,无须我们自己编写。
第 02 行创建了一个线性回归模型实例 LR。
第 03 行用于在训练集上拟合数据,在 sklearn 中,训练模型的方法统称为 fit( )。由于回归分析属于监督学习,所以 fit( ) 函数提供两个参数,前者是特征数据,后者是标签数据。
第 04 行的作用就是在测试集上实施模型预测。
波士顿房价数据集中共计 13 个特征,所以至少有 13 个权值,外加一个截距,即应拟合出 14 个权值。从上面的代码输出结果可以看出,权值数量上符合预期。有了上述 14 个参数,利用之前讲过的公式,我们就很容易把线性回归模型建立起来。一旦模型建立好,用这个模型来预测新样本(如测试集数据)就水到渠成了。
np.set_printoptions(precision = 3, suppress = True)
print('w0 = {0:.3f}'.format(LR.intercept_))
print('W = {}'.format(LR.coef_))
输出
w0 = 37.937
W = [-0.121 0.044 0.011 2.511 -16.231 3.859 -0.01 -1.5 0.242 -0.011 -1.018 0.007 -0.487]
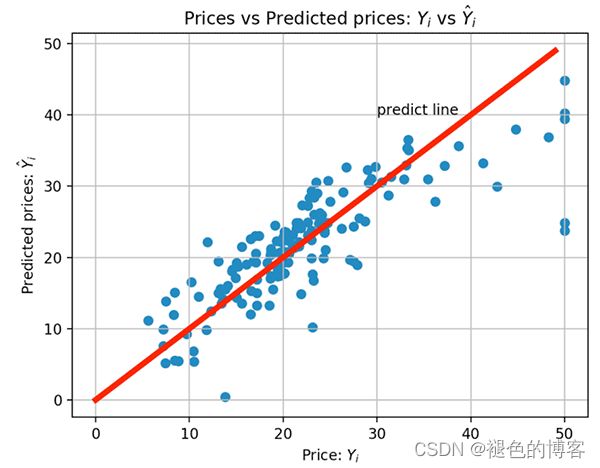
绘制预测结果
import matplotlib.pyplot as plt
import numpy as np
plt.scatter(y_test, y_pred)
plt.xlabel("Price: $Y_i$”)
plt.ylabel("Predicted prices: $\hat{Y}_i$")
plt.title("Prices vs Predicted prices: $Y_i$ vs $\hat{Y}_i$")
plt.grid()
x = np.arange(0, 50)
y = x
plt.plot(x, y, color = 'red', lw = 4)
plt.text(30,40, "predict line")