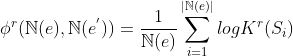bert-ini:一种基于bert的实体对齐交互模型

1 前言

---

知识图谱对齐的目标是链接不同知识库中的相等实体。为了更好的利用图结构信息和图元素信息（如名称、描述、属性），大多数工作都是通过实体间的连接关系进行图元素信息的传播。然而，由于图的异质性，对齐的实体精确度受不同邻居聚合影响较大。这篇工作提出了仅利用图元素信息的交互模型，该算法不是聚集邻居，而是计算邻居之间的交互，能够捕捉到邻居之间的细粒度匹配信息。类似地，属性之间的交互也被建模。实验结果表明，在DBP15K数据集上，对于HitRatio@1，作者的模型比最好的方法提高1.9-9.7%的性能。

2 相关背景

---

为了利用图元素信息，目前最可行的方式是采用图节点信息将节点初始化为embedding，再通过GCN的变种对邻居信息进行聚合更新其embedding。然而，不同的图谱结构高度异质，所以并不是相同的实体会有相似的邻居。例如，图1中矩形表示需要对齐的实体，圆形表示其邻居。从图中，可以看到对于G2中“english”实体在G1中找不到对应的实体。在这种情况下，使用GCN整合不同的邻居信息可能会将错误进行传播导致错误，关系数越多的节点中，这种现象就愈发明显。虽然有些工作区分了不同邻居的影响，但本质上，基于GCN的模型仍然混合了不同的图元素信息去表示一个实体。对于这个问题，HMAN将图结构信息和图元素信息分别进行模型处理，然而，这项工作忽略了邻居的图元素信息。更进一步的有，和大多数整合邻居信息的工作类似，这项工作也会导致错误信息在匹配实体之间进行传播。

图1 实体对齐

为了处理邻居或属性匹配导致的噪声信息，作者提出了一种只利用图元素信息的Bert交互模型，这种模型对实体和邻居的名称、描述、属性采用统一的处理方式。具体来说，作者模仿人类对比不同实体的处理方式，先比较实体后再比较是否具备相似的邻居。在此基础上，对于任何一段名称、描述和属性的向量嵌入，作者对每对邻居或属性采用交互的方式而不是通过聚合的方式进行处理。通过这种方式，作者可以在匹配的邻居之间获取细粒度精确的语义匹配信息以及消除不相似的邻居带来的负面影响，如图1所示。

3 问题定义

---

定义:    知识图谱：将记作为，这里属于，属于，属于 ，属于分别表示实体、关系、属性名和属性值。记做实体的跳邻居，其中第个邻居包含关系和对应的邻居实体。，记做实体的属性，这里第个属性包含一个属性名称和对应的属性值，表示不考虑跳数的实体的所有邻居。和分别表示和的元素个数。

问题 :   知识图谱对齐：给两个图谱、和一个已经对齐的实体对，作者的目标是对不同实体学习一个相似度排序函数 ，基于这个相似度函数，作者按相似度从高到低对进行排序。

4 BERT-INT模型

---

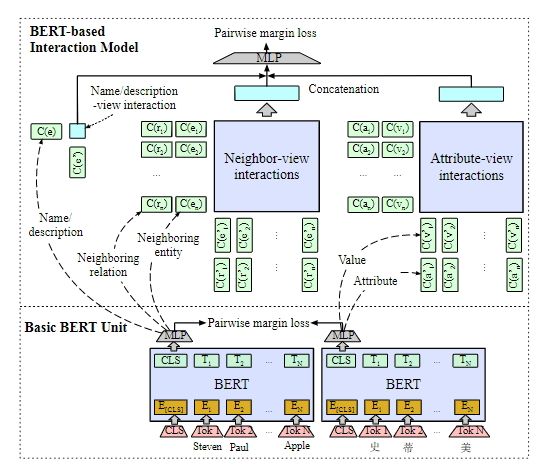
BERT-INT模型的整体框架如图2所示，它将BERT模型作为基础的表示单元对实体的名称、描述、属性和属性值进行嵌入，交互模型建立在由Bert产生的embedding之上。交互模型更进一步分为名称/描述交互视图、邻居交互视图和属性交互视图。之后采用统一的二元整合函数从邻居交互视图和属性交互视图抽取特征进一步评估实体匹配的得分。另外，为了理解邻居交互视图，作者对邻居实体之间的交互和对应的多跳的邻居关系也进行了建模。

图2 BERT-INT模型架构

4.1 bert编码器

---

作者将实体对齐作为预训练模型Bert的微调的下游任务。具体来讲，作者构建数据集，这里每个三元组包含一个查询实体，和正确的对齐实体以及从中随机选取的负样本实体。对于每一个实体数据集中的实体，作者将其实体名称/描述作为多语言Bert模型的输入，并取出CLS的embedding向量后应用ML层，如公式1所示，然后使用pairwise margin loss作为损失函数进行微调Bert，loss函数如公式2所示。

   

这里是triplet loss的距离超参，是测量和之间的距离函数。负样本由余弦相似度对两个实体进行负采样得到。

因为实体的描述具备更丰富的信息，作者优先考虑实体的描述信息，即，当实体的描述信息缺失时，才将实体名称作为实体的信息作为输入。和HMAN直接使用描述的embeddings进行实体对齐不同的是，作者在由Bert模型输出的嵌入向量之上建立交互模型进行实体对齐，这种做法可以利用下游端到端的任务对bert进行微调以及对交互模型进行训练。实际上，考虑GPU显存和训练效率，作者首先对bert进行微调压缩后再进行交互模型的最终训练。

4.2 视图交互模型

---

基于BERT单元，作者构建的交互模型包括名称/描述交互视图、邻居交互视图和属性交互视图三部分，下面分别对其进行介绍。

名称/描述交互视图

作者根据实体和的名称/描述利用bert得到其嵌入表示,并计算其余弦相似度作为名称/描述视图的交互表示。

邻居交互视图

作者在实体和实体的邻居（即和)之间构建交互模型。直观的做法是计算每个实体对的名称/描述而不是通过聚合实体或的所有邻居的名称/描述信息学习一个全局的表示，这种方法在信息抽取领域的文档搜索任务上捕捉软匹配信息和硬匹配信息时被广泛使用。具体来讲，作者基于实体和实体邻居的名称/描述利用bert获取其和，并在二者的嵌入集合基础上计算相似度矩阵，再通过一个聚合函数得到相似度特征。作者用表示实体和的邻居之间的交互矩阵，每一个元素表示为，其中和分别表示实体和的第和第个邻居，和通过公式1得到。

图3 邻居交互视图模型架构

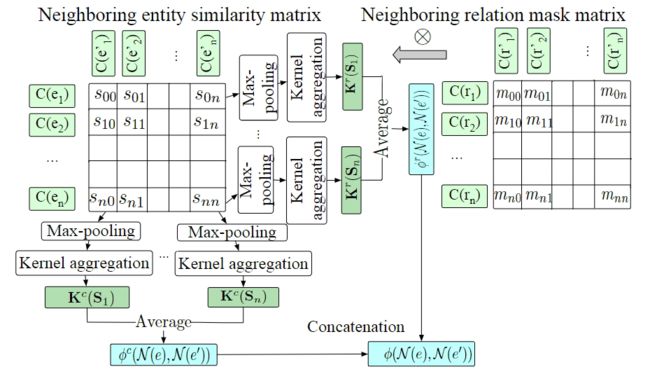
作者对相似度矩阵行和列应用成对聚合函数抽取相似度特征。CNN和RNN网络通常作为从两个句子的相似度矩阵抽取匹配模式的聚合函数，但和句子不同的是，实体的邻居彼此独立且无序，因此作者使用RBF聚合函数对于积累的相似度进行特征抽取。

在应用RBF核聚合函数之前，作者首先在每一行应用了最大池化操作得到，然后针对实体的第个邻居从实体的邻居中选择最可能的对齐部分。这样做的原因是，基于一一映射的假设，作者仅仅关心对于实体的第个邻居最可能的对齐实体部分对相似程度。或者说，实体的一个邻居不要求和实体的所有邻居都相似，因此除最相似的邻居之外，其它邻居将不进行考虑。所以，最大值被转移到基于行的特征向量，即，第个元素被传到第个以为平均值为方差的RBF核函数，然后所有行的进行平均后得到相似嵌入向量，具体如公式3所示：

这里n是所有实体中最多数量邻居的个数。如果当前实体的邻居数量少于n相似度矩阵对应的部分元素将被填充为0。核函数的使用是将一个维度的相似度扩展为L维度的相似度来加强消岐能力，这里这个和的核仅仅考虑邻居间的精确匹配，其余的则是捕捉不同邻居间的语义匹配。

上述的处理聚合行的特征的方式，影响着每一个e的邻居有多相似于实体e'的邻居。类似的，作者对于相似性矩阵S的列也进行了同样的操作从而来捕捉实体e'的每个邻居和实体e的邻居有多相似。最后行聚合向量和列聚合向量进行拼接作为最终的相似度嵌入向量，如公式4所示。

上述公式中表示从concat操作，邻居交互视图如图3所示。

邻居关系掩码矩阵

如果一对实体的关系是对齐的话，那么这对实体对齐的可信度更高。或者说，对于三元组和另一组三元组，如果和很相似，和也非常相似的话，那么和对齐的可能性更大。根据这个假设，作者不仅仅计算邻居实体的相似度矩阵，也会对对应邻居的关系计算其相似度矩阵。矩阵可以看做为一个掩码矩阵并且和矩阵的对应元素进行相乘，例如。为了计算矩阵，作者需要对每个邻居的关系进行嵌入。一种比较常用的做法基于的假设是，如果一对实体和另一对实体更相似的话，那么其对应的关系也更相似。具体来讲，作者对每个关系的头实体的嵌入向量和尾实体的嵌入向量取平均拼接后作为对应关系的嵌入表示。

多跳邻居之间的交互

直观来看，一跳邻居在判断实体对齐具备最重要的影响。但之前有工作提到，多跳邻居在一些场景下能够影响实体对齐的结果，由于两个KG的异质性，中一个实体的直接近邻可能会出现为中对应实体的远距离近邻。因此，作者仍然会考虑多跳邻居之间的交互。具体来讲，给定一跳邻居和以及多跳邻居、，作者在和之间、和之间、和之间以及和之间使用公式3建立交互矩阵，然后使用公式4抽取相似度向量，并拼接后作为最终的相似邻居嵌入。

属性交互视图

作者在属性和之间也建立了交互。和每个实体拥有唯一的名称或描述不同的是，属性是一个属性-值对集合，这种集合与关系-实体对集合类似。所以类似的，对于属性交互视图，作者仍然通过聚合实体和的属性获取其表示。具体来讲，如图3所示，作者使用属性值之间的相似计算作为矩阵，使用属性名之间的相似度作为矩阵。基于的假设是如果两个实体的属性值对比较相似的话，那么这两个实体相似的可能性更大。然后使用公式3和4进行相同的后续操作，得到。这里，作者会忽略邻居的属性，一方面合并邻居的属性会造成嵌套交互，造成效率低下。另一方面，对于需要对齐的实体和，他们自己的属性才是最重要的信息。

最终组合

作者将得到的，和相似度向量进行拼接后应用MLP得到最终和的相似度，如公式5所示。 

  

最终，作者基于得到的采用公式2得到损失函数值，并进一步优化MLP的参数。需要注意的是，BERT的参数已在第4.1节提到的工作中得到微调，所以在此阶段将进行冻结。

4.3 实体对齐

---

给出图G的实体e，作者在召回阶段从图谱G'中快速的召回前k个候选实体，之后从候选实体中再进行精确推断得到实体e的真正另一对齐实体。具体来讲，作者利用公式1获得所有实体的嵌入，并计算实体e和G'所有实体的余弦距离，并返回前K个相似的候选对齐实体。之后对于每个候选实体采用交互模型进一步推断匹配得分并进行排序评估。候选集的获取对于实体对齐任务能够大大提高对齐效率。

5 实验

---

5.1 实体对齐

---

作者使用交叉语言数据集DBP15K和单语言数据集 DWY100K并且使用HitRatio@K (K=1,10)和MRR指标进行模型性能评估。公式1中bert的维度为768,MLP的维度设置为300，公式5中的MLP维度设置为1，最多的邻居和属性超参设置为50。公式3中，作者使用20个语义匹配核，这里从0.025到0.975不等（使用0.05进行迭代）并且将所有的设置为0.1，精确匹配核则设置为和。召回集的数据量则设置为50（可以做到99%的召回率准确率）。公式2中的margin m在微调bert时设置为3，训练交互模型阶段则设置为1。

5.2 实验结果

---

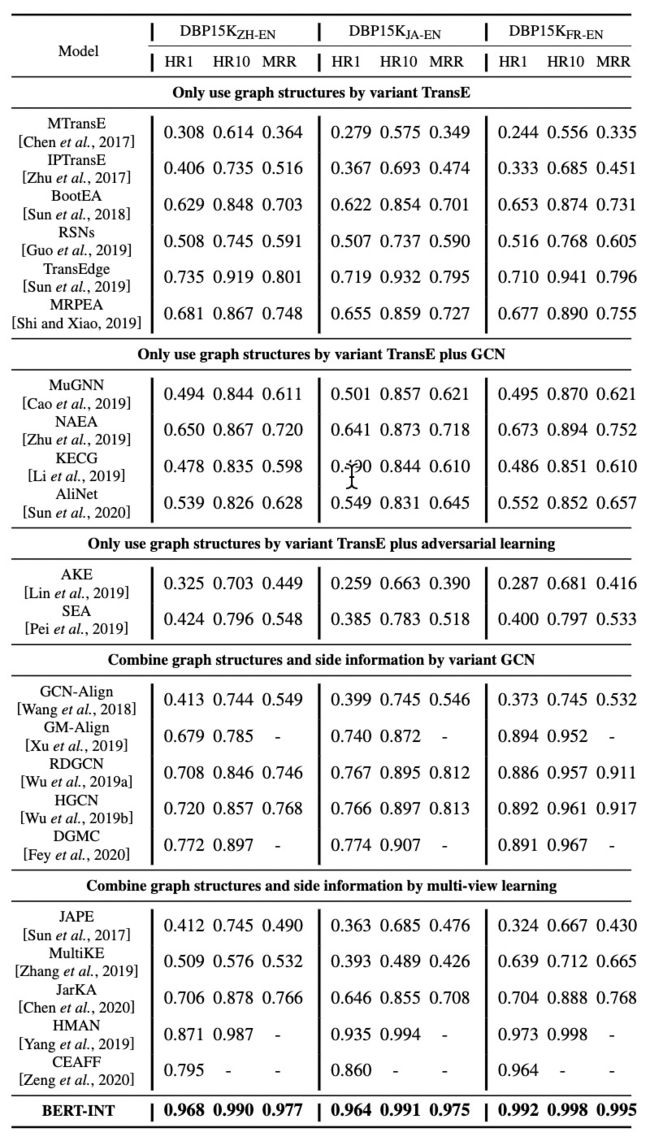
作者计算当前能够获取到代码或结果的最好模型，但一些方法由于代码实现问题没有被比较。实际操作中，作者将对比分为两类，一类是利用图结构信息，另一类是利用图元素信息。更近一步，作者将实验分为更细粒度的三类，分别为：TransE的变种、TransE和GCN结合的变种，TransE的变种和对抗学习的结合（更细粒度的分为GCN的变种与多视图学习）。表1展示了DBP15k数据集的整体表现，得到的结论是结合图元素信息时比仅仅考虑图结构信息能得到更好的表现。

消融实验

归纳学习

6 结论

---

这项工作基于BERT嵌入建立邻域或属性间的交互来解决知识图谱实体对齐问题，从而获得邻域或属性之间的细粒度匹配。与其他模型相比，提出的模型可以达到最好的性能，并且可以实现归纳学习。

BERT-INT:A BERT-based Interaction Model For Knowledge Graph Alignment

欢迎关注微信公众号，文章会同步更新在公众号,如需转载请标注来源

着眼未来科技，追踪研究传播最新思想、最新理论，打开最新世界。