第十五章 第十五章 异步A3C(Asynchronous Advantage Actor-Critic，A3C)-强化学习理论学习与代码实现（强化学习导论第二版）

获取更多资讯，赶快关注上面的公众号吧！

【强化学习系列】

• 第一章 强化学习及OpenAI Gym介绍-强化学习理论学习与代码实现（强化学习导论第二版）
• 第二章 马尔科夫决策过程和贝尔曼等式-强化学习理论学习与代码实现（强化学习导论第二版）
• 第三章 动态规划-基于模型的RL-强化学习理论学习与代码实现（强化学习导论第二版）
• 第四章 蒙特卡洛方法-强化学习理论学习与代码实现（强化学习导论第二版）
• 第五章 基于时序差分和Q学习的无模型预测与控制-强化学习理论学习与代码实现（强化学习导论第二版）
• 第六章 函数逼近-强化学习理论学习与代码实现（强化学习导论第二版）
• 第七章 深度强化学习-深度Q网络系列1（Deep Q-Networks，DQN）
• 第八章 深度强化学习-Nature深度Q网络(Nature DQN)
• 第九章 深度强化学习-Double DQN
• 第十章 深度强化学习-Prioritized Replay DQN
• 第十一章 策略梯度（Policy Gradient）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十二章 演员评论家（Actor-Critic）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十三章 确定性策略梯度（Deterministic Policy Gradient Algorithms，DPG）-强化学习理论学习与代码实现（强化学习导论第二版）
• 第十四章 深度确定性策略梯度（Deep Deterministic Policy Gradient Algorithms，DDPG）-强化学习理论学习与代码实现（强化学习导论第二版）
• (本文)第十五章 第十五章 异步A3C(Asynchronous Advantage Actor-Critic，A3C)-强化学习理论学习与代码实现（强化学习导论第二版）
  

Asynchronous Methods for Deep Reinforcement Learning

1 介绍

深度神经网络优越的表达能力可以使强化学习(RL)算法在大规模状态空间问题上有效地执行。然而，以往认为简单的在线RL算法与深度神经网络相结合从根本上是不稳定的，所有后来就有了经验回放（第七章 深度强化学习-深度Q网络系列1（Deep Q-Networks，DQN））和双网络结构（第九章 深度强化学习-Double DQN），就是为了消除样本间的相关性和稳定网络的训练过程。

基于经验回放的Deep RL虽然在Atari游戏上取得了空前的成功，但是经验回放也有明显的不足：交互过程中需要更大的内存和更多的计算量，而且还需要能够根据旧策略生成的数据进行更新的离策略学习算法。

Google DeepMind的Volodymyr Mnih提出了一种不同的深度强化学习范式，不再借助经验回放，而是在环境的多个实例上并行地异步执行多个代理，这种并行性还将代理数据分解为一个更稳定的过程，因为在任何给定的时间步上，并行代理都将经历各种不同的状态。这个简单的idea同样支持其他基本的在策略RL算法（如Sarsa, n-step方法，演员批评家方法），以及离策略RL算法（如Q-learning），能够鲁棒有效地应用深度神经网络。

并行强化学习地另一个实际的益处是不再过度依赖GPU或大规模分布式架构，仅仅使用标准的多核CPU就可以在更短的时间内，以更少的资源消耗获得更好的结果。

并行强化学习的代表asynchronous advantage actorcritic (A3C)还可以解决连续控制问题和3D迷宫问题，可以说A3C应该是目前为止最通用且最成功的强化学习了。

2 强化学习背景

在标准强化学习中，代理在多个离散时间步上与环境$\mathcal{E}$交互，在每一个时间步$t$,代理感知状态环境状态$s_t$并根据策略$\pi$从其可选动作集合$\mathcal{A}$中选择动作$a_t$，之后代理感知下一状态$s_{t+1}$并获得一个标量奖励$r_t$。不断重复该过程，直到代理到达终止状态。回报$R_t={\sum }_{k=0}^{\infty }{\gamma }^k{r}_{t+k}$为时间步$t$之后的总累积折扣（折扣因子$\gamma \in (0,1]$）奖励，代理的目标就是最大化每个状态$s_t$之后的期望回报。

动作值函数$Q^{\pi }(s,a)=\mathbb{E}\left[R_t|s_t=s,a\right]$为遵循策略$\pi$时在状态$s_t$下采取动作$a$的期望回报。最优值函数$Q^{\ast }(s,a)={\max }_{\pi }{Q}^{\pi }(s,a)$为任意策略下状态$s$和动作$a$的最大动作值。类似地，在策略$\pi$下状态$s$的价值定义为$V^{\pi }(s)=\mathbb{E}\left[R_t|s_t=s\right]$，即遵循策略$\pi$从状态$s$开始的期望回报。

在基于价值的无模型强化学习方法中，动作值函数是通过值函数近似器表达的，如神经网络。令$Q(s,a;\theta )$为带有参数$\theta$的近似动作值函数，其中$\theta$的更新可以根据各种强化学习算法，如$Q$学习算法的目的就是直接逼近最优动作值函数$Q^{\ast }(s,a)\approx Q(s,a;\theta )$。在单步$Q$学习中，动作值函数$Q(s,a;\theta )$的参数$\theta$可以通过迭代最小化一系列损失函数来学习，其中第$i$个损失函数可以定义为：

$$L_i\left({\theta }_i\right)=\mathbb{E}{\left(r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime };{\theta }_{i-1}\right)-Q\left(s,a;{\theta }_i\right)\right)}^2$$

其中$s^{\prime }$为状态$s$的下一状态。

上述方法称为单步$Q$学习，因为其将动作值$Q(s,a)$朝单步回报$r+\gamma {\max }_{a^{\prime }}Q\left(s^{\prime },a^{\prime };\theta \right)$进行更新，这种方法的缺点是获得的奖励$r$仅会直接影响导致该奖励的状态动作对$(s,a)$的价值，而其他状态只能间接地通过更新后的$Q(s,a)$进行影响，这就会导致学习过程缓慢，因为需要多次更新才能将奖励转播至之前的相关状态动作。

一种快速转播奖励的方式就是使用$n$步回报，其中，将$Q(s,a)$向$n$步回报$r_t+\gamma r_{t+1}+\cdots +{\gamma }^{n-1}{r}_{t+n-1}+{\max }_a{\gamma }^{n}Q\left(s_{t+n},a\right)$进行更新，将导致单个奖励$r$直接影响前$n$个状态动作对的值,从而使得将奖励传播到相关状态-动作对的过程可能更有效。

和基于值函数的方法不同，基于策略的无模型方法直接参数化策略$\pi (a|s;\theta )$,并通过对$\mathbb{E}[R_t]$进行梯度上升来更新参数$\theta$,Williams提出的REINFORCE算法族就是其中的一种方法，标准的REINFORCE沿着${\nabla }_{\theta }\log \pi \left(a_t|s_t;\theta \right)R_t$的方向更新策略参数$\theta$，其中${\nabla }_{\theta }\log \pi \left(a_t|s_t;\theta \right)R_t$为${\nabla }_{\theta }\mathbb{E}[R_t]$的无偏估计，还可以将回报减去一个学习到的状态值$b_t(s_t)$,即基准，在保持无偏的同时降低估计的方差，此时的梯度就是${\nabla }_{\theta }\log \pi \left(a_t|s_t;\theta \right)\left(R_t-b_t\left(s_t\right)\right)$。

通常将值函数的估计值当作基准$b_t\left(s_t\right)\approx V^{\pi }\left(s_t\right)$，进一步降低策略梯度估计的方差。当将近似值函数作为基准时，用于缩放策略梯度的$R_t-b_t$可以看成是在状态$s_t$下动作$a_t$的优势的估计，或者优势函数为$A\left(a_t,s_t\right)=Q\left(a_t,s_t\right)-V\left(s_t\right)$，因为$R_t$为$Q\left(a_t,s_t\right)$的估计，$b_t$为$V\left(s_t\right)$的估计。这个方法可以看成是一种演员-评论家架构，其中策略$\pi$为演员，而基准$b_t$为评论家。

3 异步强化学习框架

这里将介绍四种不同的多线程异步算法：单步Sarsa、单步Q学习、n步Q学习和优势演员评论家算法。设计这些方法的目的是找到能够可靠地训练深度神经网络策略且不需要大量资源的RL算法。虽然不同的RL方法差别很大，如演员评论家为在策略策略搜索方法，$Q$学习为离策略基于值的方法，但是可以通过两种思想使得这四种算法变得实用。

首先，在一台机器的不同CPU线程上使用异步演员学习器，在一台机器上学习可以消除发送梯度和参数的通讯成本。

其次，多个演员学习器并行运行可以探索环境的不同部分，而且还可以在不同的演员学习器上使用不同的探索策略以最大化多样性。通过在不同的线程中运行不同的探索策略，与应用在线更新的单个代理相比，多个参与者-学习者并行应用在线更新时对参数所做的总体更改在时间上的相关性可能更小，因此也就不再需要经验回放，仅仅依靠执行不同探索策略的并行演员就可以实现稳定训练。

除此之外，使用多个并行演员学习器还有诸多实际好处。

• 首先，训练时间的减少与并行的演员学习器的数量大致成线性；
• 其次，由于不再依赖经验回放，就可以使用在策略RL，如Sarsa和演员评论家，来稳定地训练神经网络。

3.1 异步单步$Q$学习

每个线程都与环境的副本进行交互，在每一步都使用一个共享的且延迟更新的目标网络来计算$Q$学习损失的梯度，在应用梯度之前，先累加一定时间步的梯度。

3.2 异步单步Sarsa不同的

该算法与算法1基本相同，除了$Q(s,a)$使用了一个不同的目标值，其使用的是$r+\gamma Q\left(s^{\prime },a^{\prime };{\theta }^{-}\right)$，$a^{\prime }$为在状态$s^{\prime }$.

3.3 异步n步$Q$学习

该算法采用了前向视角，原因是当使用基于动量的方法训练神经网络和通过时间反向传播时，使用前向视图更容易。在进行一次更新时，算法首先使用其探索策略选择$t_{max}$次动作，或到达终止状态，从而就得到了自上次更新后的$t_{max}$个奖励值，然后为自上次更新后的每一个状态-动作对的$n$步$Q$学习计算梯度。

3.4 异步优势演员评论家

该算法中，同时有策略$\pi \left(a_t|s_t;\theta \right)$和值函数$V\left(s_t;{\theta }_v\right)$的估计，策略和值函数每$t_{max}$个动作或到达终止状态后更新一次，算法更新可以看成是${\nabla }_{{\theta }^{\prime }}\log \pi \left(a_t|s_t;{\theta }^{\prime }\right)A\left(s_t,a_t;\theta ,{\theta }_v\right)$，其中$A\left(s_t,a_t;\theta ,{\theta }_v\right)$是优势函数${\sum }_{i=0}^{k-1}{\gamma }^i{r}_{t+i}+{\gamma }^{k}V\left(s_{t+k};{\theta }_v\right)-V\left(s_t;{\theta }_v\right)$的估计，$k$因状态不同而不同，最大为$t_{max}$。

相比Actor-Critic，A3C的优化主要有3点，分别是异步训练框架，网络结构优化，Critic评估点的优化。其中异步训练框架是最大的优化。

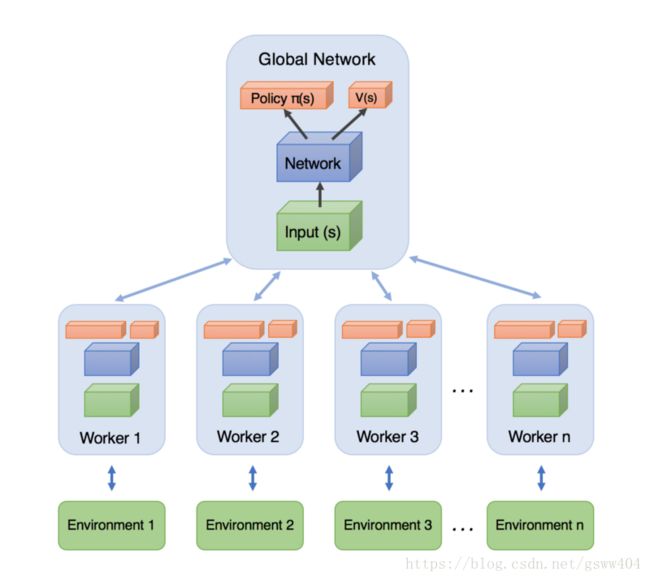
首先来看这个异步训练框架，如下图所示：

图中上面的Global Network就是共享的公共部分，主要是一个公共的神经网络模型，这个神经网络包括Actor网络和Critic网络两部分的功能。下面有n个worker线程，每个线程里有和公共的神经网络一样的网络结构，每个线程会独立的和环境进行交互得到经验数据，这些线程之间互不干扰，独立运行。

每个线程和环境交互到一定量的数据后，就计算在自己线程里的神经网络损失函数的梯度，但是这些梯度却并不更新自己线程里的神经网络，而是去更新公共的神经网络。也就是n个线程会独立的使用累积的梯度分别更新公共部分的神经网络模型参数。每隔一段时间，线程会将自己的神经网络的参数更新为公共神经网络的参数，进而指导后面的环境交互。

可见，公共部分的网络模型就是我们要学习的模型，而线程里的网络模型主要是用于和环境交互使用的，这些线程里的模型可以帮助线程更好的和环境交互，拿到高质量的数据帮助模型更快收敛。

4 代码练习

代码搭建部分参照了莫烦python，完整代码点击这里获取。

Actor Critic 网络

# 这个 class 可以被调用生成一个 global net.
# 也能被调用生成一个 worker 的 net, 因为他们的结构是一样的,
# 所以这个 class 可以被重复利用.
class ACNet(object):
    def __init__(self, globalAC=None):
        # 当创建 worker 网络的时候, 我们传入之前创建的 globalAC 给这个 worker
        if 这是 global:   # 判断当下建立的网络是 local 还是 global
            with tf.variable_scope('Global_Net'):
                self._build_net()
        else:
            with tf.variable_scope('worker'):
                self._build_net()

            # 接着计算 critic loss 和 actor loss
            # 用这两个 loss 计算要推送的 gradients

            with tf.name_scope('sync'):  # 同步
                with tf.name_scope('pull'):
                    # 更新去 global
                with tf.name_scope('push'):
                    # 获取 global 参数

    def _build_net(self):
        # 在这里搭建 Actor 和 Critic 的网络
        return 均值, 方差, state_value

    def update_global(self, feed_dict):
        # 进行 push 操作

    def pull_global(self):
        # 进行 pull 操作

    def choose_action(self, s):
        # 根据 s 选动作

Worker

每个 worker 有自己的 class, class 里面有他的工作内容 work。

class Worker(object):
    def __init__(self, name, globalAC):
        self.env = gym.make(GAME).unwrapped # 创建自己的环境
        self.name = name    # 自己的名字
        self.AC = ACNet(name, globalAC) # 自己的 local net, 并绑定上 globalAC

    def work(self):
        # s, a, r 的缓存, 用于 n_steps 更新
        buffer_s, buffer_a, buffer_r = [], [], []
        while not COORD.should_stop() and GLOBAL_EP < MAX_GLOBAL_EP:
            s = self.env.reset()

            for ep_t in range(MAX_EP_STEP):
                a = self.AC.choose_action(s)
                s_, r, done, info = self.env.step(a)

                buffer_s.append(s)  # 添加各种缓存
                buffer_a.append(a)
                buffer_r.append(r)

                # 每 UPDATE_GLOBAL_ITER 步 或者回合完了, 进行 sync 操作
                if total_step % UPDATE_GLOBAL_ITER == 0 or done:
                    # 获得用于计算 TD error 的 下一 state 的 value
                    if done:
                        v_s_ = 0   # terminal
                    else:
                        v_s_ = SESS.run(self.AC.v, {self.AC.s: s_[np.newaxis, :]})[0, 0]

                    buffer_v_target = []    # 下 state value 的缓存, 用于算 TD
                    for r in buffer_r[::-1]:    # 进行 n_steps forward view
                        v_s_ = r + GAMMA * v_s_
                        buffer_v_target.append(v_s_)
                    buffer_v_target.reverse()

                    buffer_s, buffer_a, buffer_v_target = np.vstack(buffer_s), np.vstack(buffer_a), np.vstack(buffer_v_target)

                    feed_dict = {
                        self.AC.s: buffer_s,
                        self.AC.a_his: buffer_a,
                        self.AC.v_target: buffer_v_target,
                    }

                    self.AC.update_global(feed_dict)    # 推送更新去 globalAC
                    buffer_s, buffer_a, buffer_r = [], [], []   # 清空缓存
                    self.AC.pull_global()   # 获取 globalAC 的最新参数

                s = s_
                if done:
                    GLOBAL_EP += 1  # 加一回合
                    break   # 结束这回合

Worker 并行工作

这里才是真正的重点! Worker 的并行计算。

with tf.device("/cpu:0"):
    GLOBAL_AC = ACNet(GLOBAL_NET_SCOPE)  # 建立 Global AC
    workers = []
    for i in range(N_WORKERS):  # 创建 worker, 之后在并行
        workers.append(Worker(GLOBAL_AC))   # 每个 worker 都有共享这个 global AC

COORD = tf.train.Coordinator()  # Tensorflow 用于并行的工具

worker_threads = []
for worker in workers:
    job = lambda: worker.work()
    t = threading.Thread(target=job)    # 添加一个工作线程
    t.start()
    worker_threads.append(t)
COORD.join(worker_threads)  # tf 的线程调度