一、时间和空间复杂度基本概念
1、影响系统性能的因素有哪些?
影响系统性能的因素有很多,把这些因素分为三大类
1、算法理论上的计算复杂度
2、开发实现的方案和硬件设备的规格
3、算法理论上的计算复杂度、开发实现的方案和硬件设备的规格
2、复杂度是什么?
算法复杂度是一个比较抽象的概念,通常只是一个估计值,它用于衡量程序在运行时所需要的资源用于比较不同算法的性能好坏
我们通常所说的时间复杂度是指渐进时间复杂度,标识程序运行时间随着问题复杂度增加而变化的规律
空间复杂度是指渐进空间复杂度,标识程所需要的存储的存储空间复杂度增加而变化的规律
二、复杂度分析的6个通用法则
1、四则运算法则
代码的添加,以为着计算机操作的增加,也就是时间复杂度的增加
如果代码是平行增加的,就是加法
如果是循环、嵌套或者函数的嵌套,那么就是乘法
加法
比如二分查找中
1、第一步是对长度为n的数组排序,时间复杂度是O(nlogn)
2、第二步是在这个已排序的数组中进行查找 时间复杂度是 O(logn)
这两部分是平行的,所以计算时间复杂度时可以使用加法,所以时间复杂度是:O(nlogn)+O(logn)。
你还记得在第3讲我讲的查字典的例子吗?
String[] dictionary = {"i", "am", "one", "of", "the", "authors", "in", "geekbang"};
Arrays.sort(dictionary); // 时间复杂度为 O(nlogn)
String wordToFind = "i";
boolean found = Lesson3_3.search(dictionary, wordToFind); // 时间复杂度 O(logn)
if (found) {
System.out.println(String.format(" 找到了单词 %s", wordToFind));
} else {
System.out.println(String.format(" 未能找到单词 %s", wordToFind));
}1、Arrays.sort(dictionary),我用了Java 自带的排序函数,时间复杂度为 O(nlogn),
2、而Lesson3_3.search 是我自己实现的二分查找,时间复杂度为 O(logn)
3、两者是并行的,并以此执行,因此总的时间复杂度是两者相加
对于空间复杂度,同样如此,
需要注意的是,空间复杂度看的是对内存空间的使用,而不是计算的次数,如果语句中没有新开辟空间,那么无论是平行增加还是嵌套增加代码,都不会增加空间复杂度
2、主次分明法则
这个法则主要是运用了数量级和运算法则优先级的概念,在刚刚介绍的第一个法则中,我们会对代码不同部分所产生的复杂度进行相加或相乘
使用加法或减法时,你可能会遇到不同数量级的复杂度,这个时候,我们只需要看最高数量级的,而忽略常量、系数和较低数量级的复杂度
这个法则对于空间复杂度,同样使用
注意,这个法则对于乘法或除法并不使用,因为乘法和除法会改变参与运算的复杂度的数量级
3、齐头并进法则
这个法则主要运用了多元变量的概念,其核心思想是复杂度可能受到多个因素的影响,在这种情况下,我们要同时考虑所有因素,并在复杂度公式中体现出来
使用动态规划解决编辑距离问题,从解决方案的推导和代码可以看出,这个问题设计两个因素
1、参与比较的第一个字符串的长度n和第二个字符串的长度m
2、代码使用了两次嵌套循环,第一层循环的长度是n,第二层循环的长度为m
3、根据乘法法则,时间复杂度为O(n*m)。而空间复杂度,很容易从推导结果的状态转移表得出,也是O(n*m)
4、排列组合法则
排列组合的思想不仅出现在数学模型的设计中,同样也会出现在复杂度分析中,它经常会用在最好、最坏和平均复杂度分析中
5、一图千言法则
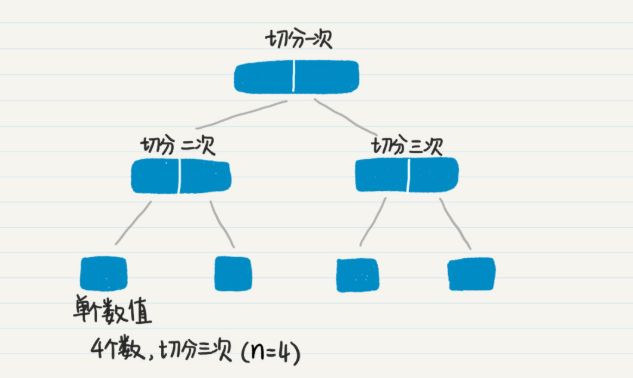
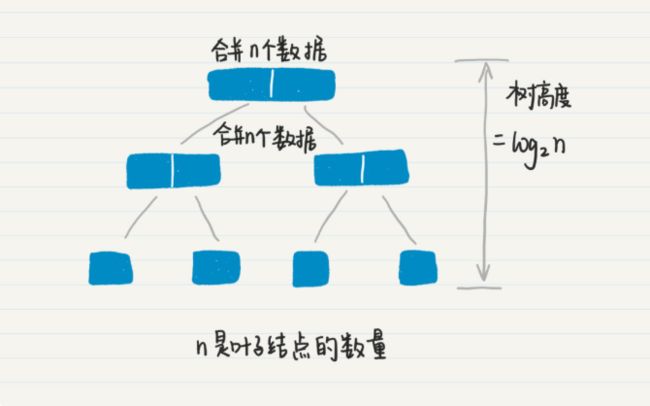
1、归并排序为例
1、数据切分阶段
2、数据合并阶段
两个极端加起来的时间复杂度为O(n-1)+nlog2n,最终简化为 nlogn。是不是很直观?
我们在放出我们之前讲的二分查找所用的图,你可以结合这个例子进一步理解
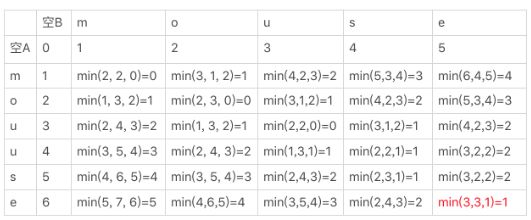
2、动态规划
动态规划的时候我们经常要画出状态转移的表格,看到这类表格,
我们可以很容易地得出该算法的时间复杂度和空间复杂度,m 为第一个字符串的长度,n 为第二个字符串的长度。
所以,我们很快就能得出这种算法的时间复杂度为O(3m*n),简写为 O(m*n),空间复杂度为 O(m*n)
6、时空互换法则
在给定的计算量下,通常时间复杂度和空间复杂度呈现数学中的反比关系。这就说明,如果我们没法降低整体的计算量,
那么也许可以通过增加空间复杂度来达到降低时间复杂度的目的或者反之,通过藏家时间复杂度来降低空间复杂度
缓存系统
在没有缓存系统的时候,每次请求都要服务器来处理,因此时间复杂度比较高,如果使用了缓存系统
那么我们会消耗更多的内存空间,但是降低了请求相应的时间
说道这、你也许会问,在使用广度优先策略优化聚合操作的时候,无论是时间还是空间复杂度,都大幅降低了啊?请注意,
这里的互换法则有个前提条件,就是计算两固定,而聚合操作的优化,是利用了广度优先的特点,大幅减少了整体的计算量,
因此可以保证时间和空间复杂度都的到降低
三、思考题
请尝试使用本次介绍的规则,分析一下双向广度优先搜索的时间和空间复杂度
思考题感觉要根据具体图的情况来看具体时间复杂是多少,就之前的六度关系的例子,假设把关系看作是一个树,每个结点都有 n 个子结点,要确认两个人是几度好友,
也就是确认两个结点相距多少层,如果是单向广度优先搜索,时间复杂度 O(n^degree),双向可以运用加法法则,两边同时出发,时间复杂度 2 * O(n^(degree/2)),
空间复杂度是队列中暂存的结点的最大值,和时间复杂度一样