【数据结构】(多图、gif)红黑树的工作原理(内附伪代码及python代码)
在本文中,我们将研究什么是红黑树,以及它为什么有用。我们将了解红黑树的各种操作及其算法、示例和python代码。稍后我们还将介绍红黑树的各种优点、缺点和应用。
1. 1 什么是红黑树?
红黑树是二叉搜索树的变种,具有自平衡特性。红黑树也称为对称二叉B树。红黑树的每个节点都包含一个额外的属性,表示节点的颜色,特别是红色或黑色。这些颜色在树的节点中的重要性确保了在节点的插入和删除操作中树是平衡的。因此,红黑树遵循以下属性:
1、基本属性:红黑树是一个二叉搜索树
2、节点红/黑规则:树的每个节点要么是红色要么是黑色
3、根节点规则:根节点的颜色属性始终为黑色
4、叶子节点规则:树的每一片叶子都是黑色的
5、红节点规则:如果父节点的颜色为红色,则子节点始终为黑色。因此,不会有两个连续的红色节点
6、深度规则:从根节点到任何叶节点的每条路径都会经过相同个数的黑色节点

上图就是一课最简单的红黑树
1.2为什么选择红黑树?
众所周知,二叉搜索树可以保持插入数据的自然顺序,但不限制树的大小高度。考虑下面的极限情况,如果向二叉搜索树中插入10、20、30、40、50。插入新节点时树呈线性增长,所以最终树的高度就是5。这种情况下,随着树的高度线性增长,树的搜索操作将成为最坏的情况,时间复杂度就是O(n)。(n为插入节点的总数)
红黑树可以很轻松地解决这个问题。红黑树在每次插入和删除操作后都会自动维护树的高度,因此可以避免树的高度无限制地向时间复杂度最大的方向生长。正因为如此,上述情况的时间复杂度可以降低到O(logn)。(n是树中的节点数)
当然你也可以使用AVL树来平衡树的高度。但是,与AVL树相比,红黑树在平衡树的高度方面做出的结构变化更少。因此,与AVL树相比,红黑树在插入和删除操作所消耗的时间会更少。
2 红黑树的原理介绍
红黑树就是利用局部的旋转、个别节点的染色来保持树的整体深度差不超多 1。
2.1红黑树中的旋转
旋转是调整或交换树内子树节点的操作,是平衡红黑树高度的基本操作。基本上,红黑树有两种类型的轮换:
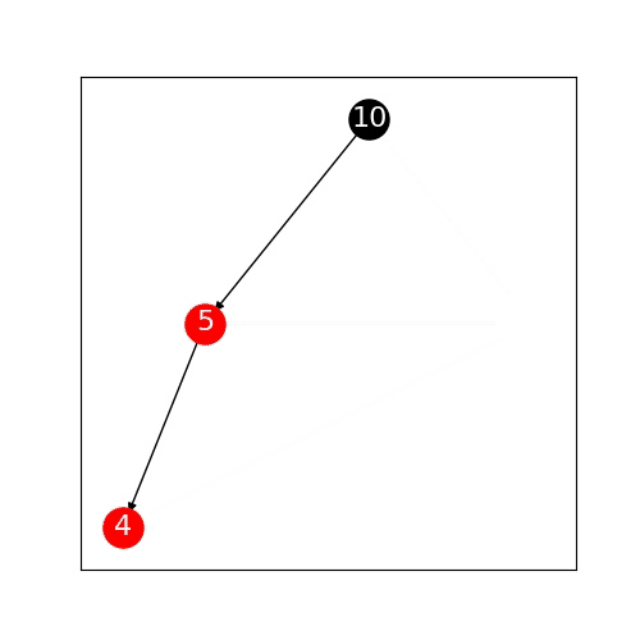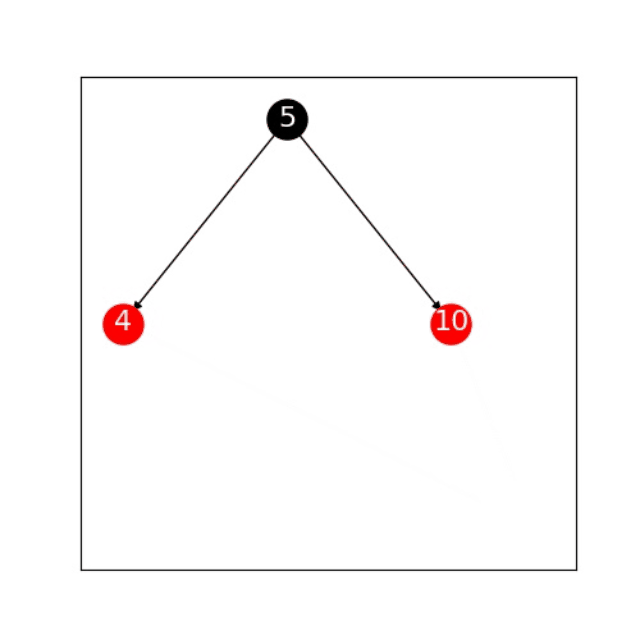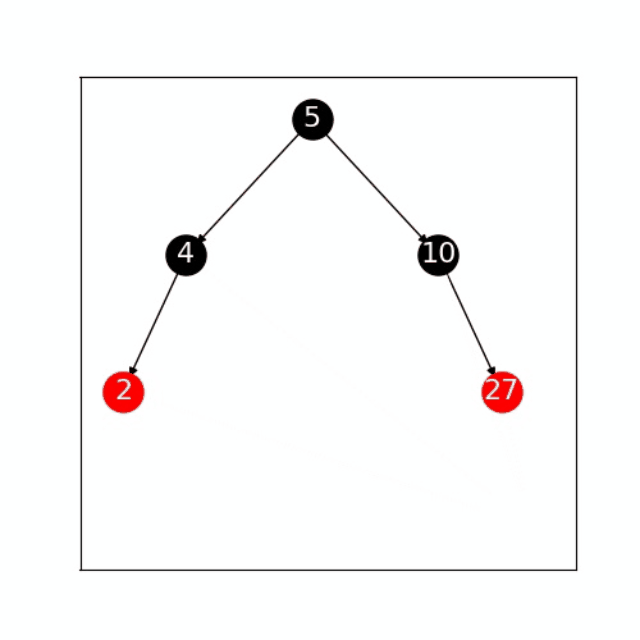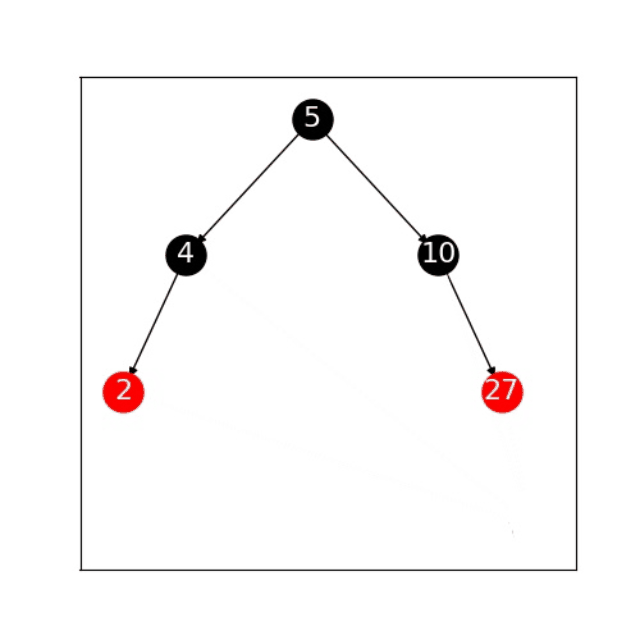
2.1.1 左旋
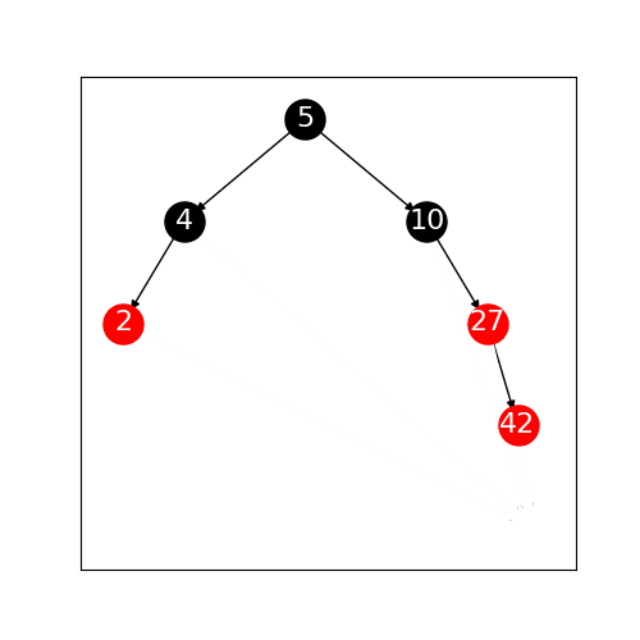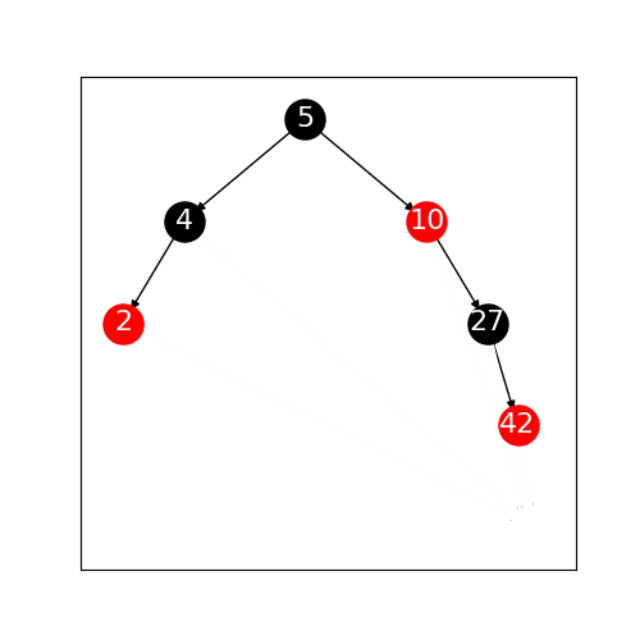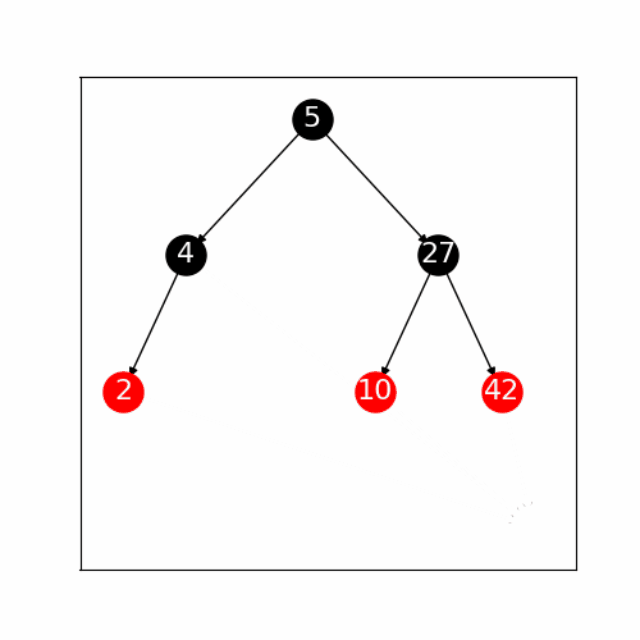
1、如果“27”有左子树,则将“10”指定为“27”左子树的父节点。
2、如果“10”的父节点为空,则将“27”指定为树的根;如果“10”是根节点的左子节点,则将“27”指定为根节3、点的左子节点
4、如果“10”是根节点的右子树,则将“27”指定为根节点的右子树
5、将“27”设为“10”的父节点
2.1.2 右旋
3.1红黑树中的操作
红黑树的两个基本操作:插入操作、删除操作
3.1.1 插入操作
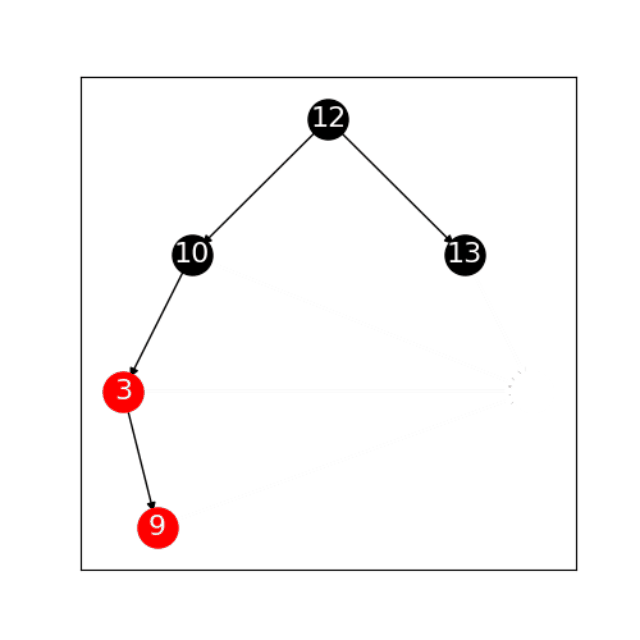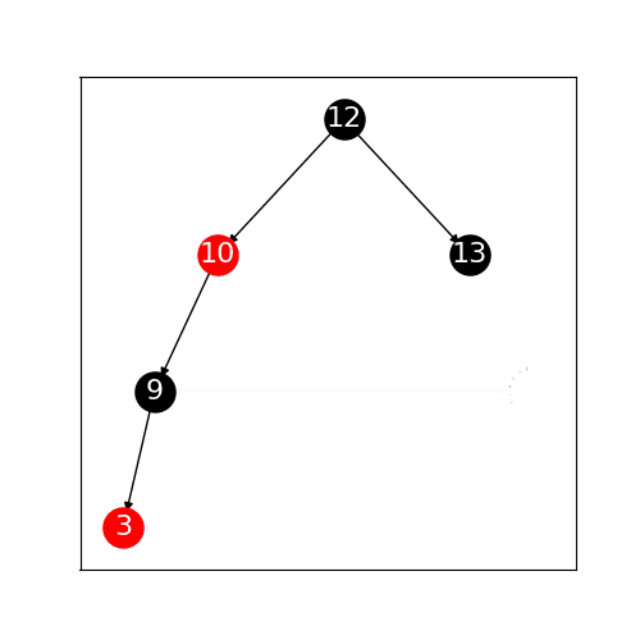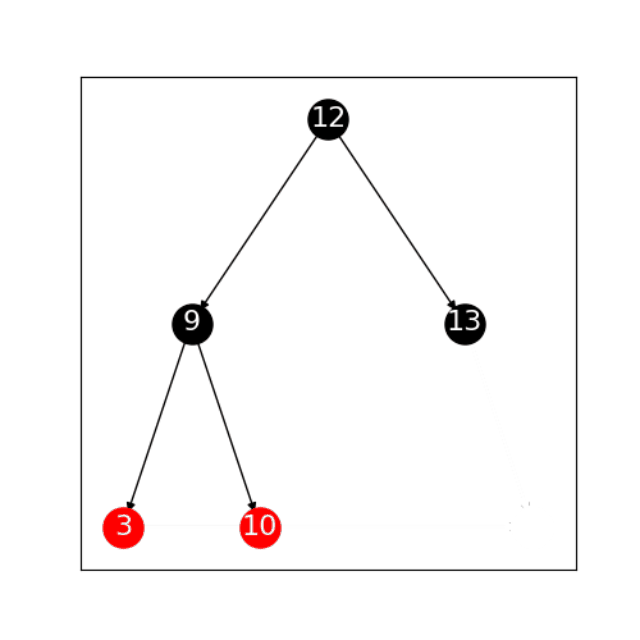
因为插入新节点不可以违反红黑树的深度规则,所以在红黑树中插入新节点时,新节点始终被当成红节点插入。如果父节点是红节点该怎么办?这时就要通过旋转来解决,而不是硬把新节点连接上。总而言之,为了避免违反深度规则,红黑树始终在做两个操作:`` 左、右旋以及重新着色*
插入的伪代码表述:
假设“x”是树的根节点 “y”是叶节点
如果树是空的 则添加NewNode作为根节点 用黑色表示
否则重复以下步骤 直到到达树的叶节点:
比较NewNode和RootNode
如果NewNode大于RootNode :
则遍历到右子树
否则 遍历左子树
如果LeafNode大于NewNode :
则将leaf的父节点分配给NewNode的父节点
否则 将NewNode分配给RightChild
将NewNode分配给LeftChild
将Null分配给LeftChild
将NewNode分配给RightChild
如果违反红黑树的属性 则应用InsertionFix算法
插入后需要执行的自平衡函数:
如果NewNode的父节点“n”为红色,则:
如果“n”是“m”的祖父母“gp”的左撇子,那么
情况1:
如果“gp”的右子树为红色,则将“gp”的两个子树的颜色设置为黑色,将“gp”的两个子树的颜色设置为红色
将“gp”分配给新节点
情况2:
如果NewNode是'n'的右子树,则将'n'分配给NewNode
左旋转新节点
情况3:
将“n”指定为黑色,“gp”指定为红色
右旋转“gp”
否则,请执行以下操作
如果“z”的“gp”的LeftChild是红色,则将“gp”的两个子树节点都设置为黑色,将“gp”设置为红色
将“gp”分配给新节点
如果NewNode是'n'的左子树,则将'n'分配给NewNode并右旋转NewNode
将“n”设置为黑色,将“gp”设置为红色
左旋转“gp”
将树的根节点设置为黑色
3.1.2 删除操作
从树中删除某个节点,可能会违反红黑树的规则。因此,从树中删除节点后,也需要执行平衡操作来确保树仍然服从红黑树的规则。
删除某个节点的代码:
如果DeletingNode的LeftChild为空,则将DeletingNode的颜色保存为OriginalColor
将DeletingNode的右子级添加为“a”
带有“a”的节点
否则,如果DeletingNode的RighChild为空
将项目从DeletingNode的左子树删除保存到“a”节点中
使用“a”移植删除节点
否则
将DeletingNode的右子树的最小值赋给“b”
将“b”的颜色保存为原始颜色
将“b”的右子树赋给“a”
如果“b”是DeletingNode的子树,则将“a”的父子树设置为“b”
否则,将“b”与“b”的右子树一起移动
带“b”的节点
用原色设置“b”的颜色
如果原始颜色为黑色,请调用DeletionFix(删除自平衡函数)
当要删除的节点颜色为黑色时,如果直接删除它而不做任何改变,就会违反红黑树规则。这时我们就可以通过假设节点“a”有额外的黑色来纠正这种情况。这样,节点“a就可以同时有两种色彩(的组合),当然这是违反规则的,所以需要在以下特定情况下删除“a”拥有的多余的黑色:
1、当“a”是根节点的子节点时
2、当“a”指向红黑节点,将“a”设置为只有一种黑色
3、当需要执行重染色或是旋转时
删除后需要执行的自平衡函数的伪代码:
重复以下步骤,直到'a'不是树的根节点,
如果'a'是其父节点的LeftChild,则'a'不是黑色,
将“n”分配给“a”的兄弟姐妹
如果“a”的父级的RightChild为红色
情况1:
将“a”父级的RightChild设置为黑色
将“a”的父项设置为红色
左旋转“a”的父对象
将“a”的父级的RightChild分配给“n”
如果'n'的RightChild和LeftChild是黑色的
情况2:
将“n”设置为红色
将“a”的父级分配给“a”
否则,如果“n”的右子代是黑色的
情况3:
将“n”的LeftChild设置为黑色
将“n”设置为红色
右转
将“a”的父级的RightChild分配给“n”
如果上述所有情况均未发生,则执行以下操作
情况4:
将“n”的颜色设置为“a”父级的颜色
将“a”的父项设置为黑色
将RightChild“n”设置为黑色
左旋转“a”的父对象
将“a”设置为树的根节点
重复上述步骤,从右向左互换,反之亦然,将“a”设置为黑色
3.2 完整代码
# Define Node
class Node():
def __init__(self,val):
self.val = val
self.parent = None
self.left = None
self.right = None
self.color = 1
inserted as Red Node
# Define R-B Tree
class RBTree():
def __init__(self):
self.NULL = Node ( 0 )
self.NULL.color = 0
self.NULL.left = None
self.NULL.right = None
self.root = self.NULL
# Insert New Node
def insertNode(self, key):
node = Node(key)
node.parent = None
node.val = key
node.left = self.NULL
node.right = self.NULL
node.color = 1
y = None
x = self.root
while x != self.NULL :
y = x
if node.val < x.val :
x = x.left
else :
x = x.right
node.parent = y
if y == None :
self.root = node
elif node.val < y.val :
y.left = node
else :
y.right = node
if node.parent == None :
node.color = 0
return
if node.parent.parent == None :
return
self.fixInsert ( node )
def minimum(self, node):
while node.left != self.NULL:
node = node.left
return node
# Code for left rotate
def LR ( self , x ) :
y = x.right
x.right = y.left
if y.left != self.NULL :
y.left.parent = x
y.parent = x.parent
if x.parent == None :
self.root = y
elif x == x.parent.left :
x.parent.left = y
else :
x.parent.right = y
y.left = x
x.parent = y
# Code for right rotate
def RR ( self , x ) :
y = x.left
x.left = y.right
if y.right != self.NULL :
y.right.parent = x
y.parent = x.parent
if x.parent == None :
self.root = y
elif x == x.parent.right :
x.parent.right = y
else :
x.parent.left = y
y.right = x
x.parent = y
# Fix Up Insertion
def fixInsert(self, k):
while k.parent.color == 1:
if k.parent == k.parent.parent.right:
u = k.parent.parent.left
if u.color == 1:
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
else:
if k == k.parent.left:
k = k.parent
self.RR(k)
k.parent.color = 0
k.parent.parent.color = 1
self.LR(k.parent.parent)
else:
u = k.parent.parent.right
if u.color == 1:
grandparent i.e, uncle node is red
u.color = 0
k.parent.color = 0
k.parent.parent.color = 1
k = k.parent.parent
conflicts
else:
if k == k.parent.right:
k = k.parent
self.LR(k)
k.parent.color = 0
k.parent.parent.color = 1
self.RR(k.parent.parent)
if k == self.root:
break
self.root.color = 0
# Function to fix issues after deletion
def fixDelete ( self , x ) :
while x != self.root and x.color == 0 :
color of x is black
if x == x.parent.left :
s = x.parent.right
if s.color == 1 :
s.color = 0
x.parent.color = 1
self.LR ( x.parent )
s = x.parent.right
# If both the child are black
if s.left.color == 0 and s.right.color == 0 :
s.color = 1
x = x.parent
else :
if s.right.color == 0 :
s.left.color = 0
s.color = 1
self.RR ( s )
s = x.parent.right
s.color = x.parent.color
x.parent.color = 0
s.right.color = 0
self.LR ( x.parent )
x = self.root
else :
s = x.parent.left
if s.color == 1 :
s.color = 0
x.parent.color = 1
self.RR ( x.parent )
s = x.parent.left
if s.right.color == 0 and s.right.color == 0 :
s.color = 1
x = x.parent
else :
if s.left.color == 0 :
s.right.color = 0
s.color = 1
self.LR ( s )
s = x.parent.left
s.color = x.parent.color
x.parent.color = 0
s.left.color = 0
self.RR ( x.parent )
x = self.root
x.color = 0
# Function to transplant nodes
def __rb_transplant ( self , u , v ) :
if u.parent == None :
self.root = v
elif u == u.parent.left :
u.parent.left = v
else :
u.parent.right = v
v.parent = u.parent
# Function to handle deletion
def delete_node_helper ( self , node , key ) :
z = self.NULL
while node != self.NULL :
value/ key and store it in 'z'
if node.val == key :
z = node
if node.val <= key :
node = node.right
else :
node = node.left
if z == self.NULL : # If Kwy is not present then deletion not possible so return
print ( "Value not present in Tree !!" )
return
y = z
y_original_color = y.color
if z.left == self.NULL :
x = z.right =
self.__rb_transplant ( z , z.right )
elif (z.right == self.NULL) :
x = z.left
self.__rb_transplant ( z , z.left )
else :
y = self.minimum ( z.right )
y_original_color = y.color
x = y.right
if y.parent == z :
x.parent = y
else :
self.__rb_transplant ( y , y.right )
y.right = z.right
y.right.parent = y
self.__rb_transplant ( z , y )
y.left = z.left
y.left.parent = y
y.color = z.color
if y_original_color == 0 :
self.fixDelete ( x )
# Deletion of node
def delete_node ( self , val ) :
self.delete_node_helper ( self.root , val )
# Function to print
def __printCall ( self , node , indent , last ) :
if node != self.NULL :
print(indent, end=' ')
if last :
print ("R----",end= ' ')
indent += " "
else :
print("L----",end=' ')
indent += "| "
s_color = "RED" if node.color == 1 else "BLACK"
print ( str ( node.val ) + "(" + s_color + ")" )
self.__printCall ( node.left , indent , False )
self.__printCall ( node.right , indent , True )
# Function to call print
def print_tree ( self ) :
self.__printCall ( self.root , "" , True )
if __name__ == "__main__":
bst = RBTree()
bst.insertNode(10)
bst.insertNode(20)
bst.insertNode(30)
bst.insertNode(5)
bst.insertNode(4)
bst.insertNode(2)
bst.print_tree()
print("\nAfter deleting an element")
bst.delete_node(2)
bst.print_tree()