工业蒸汽预测

---

前言

本文来自于天池大赛——学习赛，仅作学习使用，目标：给定经过脱敏后的锅炉传感器采集的数据，根据锅炉的工况来预测产生的蒸汽量。

一、数据探索、特征工程

1-1、导入数据包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats

import warnings
warnings.filterwarnings("ignore")
%matplotlib inline

1-2、读取数据文件

# 文本文件，需要设置分隔符为\t。

train_data = pd.read_csv('./zhengqi_train.txt', sep='\t', encoding='utf-8')
test_data = pd.read_csv('./zhengqi_test.txt', sep='\t', encoding='utf-8')
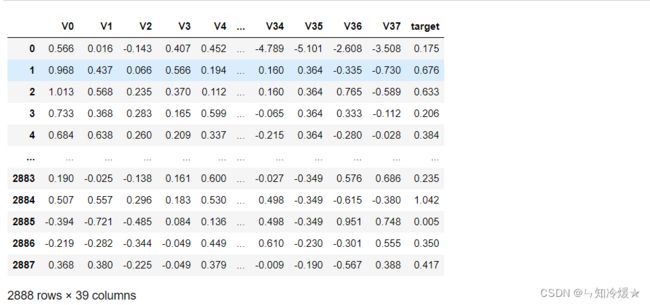
train_data

输出：

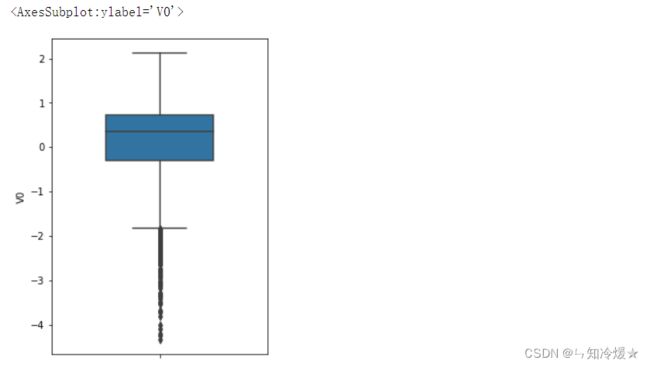
1-3、绘制箱型图探索数据

# 箱型图
fig = plt.figure(figsize=(4, 6))
# y：在y轴上显示数据
# width: 箱型图的 宽度
sns.boxplot(y=train_data['V0'], width=0.5)

输出：

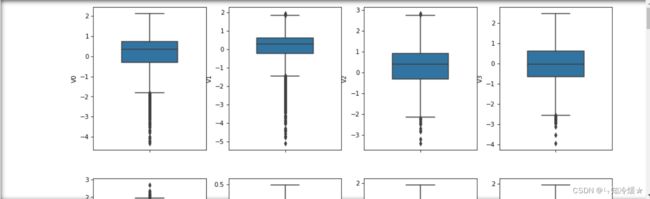
column = train_data.columns.to_list()[:-1]
fig = plt.figure(figsize=(15, 50), dpi=75)


# 从图中我们可以看出存在许多偏离较大的异常值
for i in range(38):
    plt.subplot(10, 4, i+1)
    sns.boxplot(y=train_data[column[i]], width=0.5)
    plt.ylabel(column[i], fontsize=10)
plt.show()

输出：

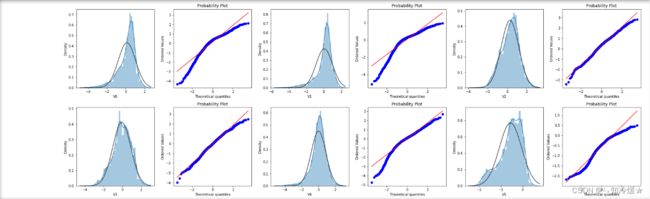
1-4、绘制QQ图查看数据分布

# QQ图是指数据的分位数和正态分布的分位数对比参照的图
# 如果数据符合正态分布，则所有的点都会落在直线上。
plt.figure(figsize=(10, 5))
ax = plt.subplot(1, 2, 1)
sns.distplot(train_data['V0'], fit=stats.norm)
ax = plt.subplot(1, 2, 2)
res = stats.probplot(train_data['V0'], plot=plt)

输出：

train_cols =6
train_rows =len(train_data.columns)
plt.figure(figsize=(4*train_cols, 4*train_rows))

i=0
for col in train_data.columns:
    i+=1
    ax = plt.subplot(train_rows, train_cols, i)
    sns.distplot(train_data[col], fit=stats.norm)
    
    i+=1
    ax=plt.subplot(train_rows, train_cols, i)
    res = stats.probplot(train_data[col], plot=plt)
plt.tight_layout()
plt.show()

输出：

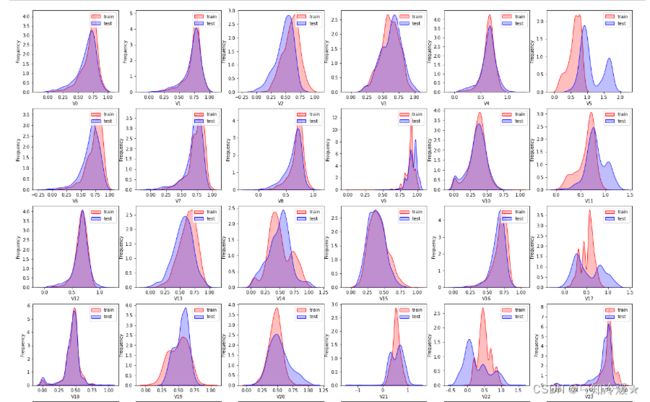
1-5、绘制Kde核密度图。

# KDE：核密度估计，对直方图的加窗平滑，
# 通过绘制KDE分布图，可以查看并对比训练集和测试集中特征变量的分布情况，发现两个数据集中分布不一致的特征变量。
plt.figure(figsize=(8,4), dpi=150)
ax = sns.kdeplot(train_data['V0'], color='Red', shade=True)
ax=sns.kdeplot(test_data['V0'], color='Blue', shade=True)
ax.set_xlabel('V0')
ax.set_ylabel('Frequency')
ax = ax.legend(['train', 'test'])

输出：

dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4*dist_cols, 4*dist_rows))
i=1

for col in test_data.columns:
    ax = plt.subplot(dist_rows,dist_cols, i)
    ax = sns.kdeplot(train_data[col], color="Red", shade = True)
    ax = sns.kdeplot(test_data[col], color="Blue", shade= True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])
    i += 1
plt.show()

输出：

1-6、绘制线性回归关系

# 主要用于分析变量之间的线性回归关系，首先查看特征变量V0与target变量的线性回归关系。
fcols = 2
frows = 1
plt.figure(figsize=(8,4), dpi=150)
ax = plt.subplot(1,2,1)
sns.regplot(x='V0', y='target', data=train_data, ax=ax,
            scatter_kws={'marker': '.', 's':3, 'alpha':0.3},
            line_kws={'color': 'k'}
    );
plt.xlabel('V0')
plt.ylabel('target')

ax = plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')

plt.show()

输出：

# 主要用于分析变量之间的线性回归关系，首先查看特征变量V0与target变量的线性回归关系。
fcols = 6
frows = len(test_data.columns)
plt.figure(figsize=(5*fcols,4*frows))

i=0
for col in test_data.columns:
    i+=1
    ax = plt.subplot(frows,fcols,i)
    sns.regplot(x=col, y='target', data=train_data, ax=ax,
                scatter_kws={'marker': '.', 's':3, 'alpha':0.3},
                line_kws={'color': 'k'}
        );
    plt.xlabel(col)
    plt.ylabel('target')
    i+=1

    ax = plt.subplot(frows,fcols,i)
    sns.distplot(train_data[col].dropna())
    plt.xlabel(col)
#     plt.show()

输出：

1-7、查看特征变量的相关性

# 对特征变量的相关性进行分析，可以发现特征变量和目标变量以及特征变量之间的关系，为在特征工程中提取特征做准备

# 在删除训练集和测试集中分布不一致的特征变量，如V5，V9，11，17， 22， 28之后，计算剩余特征变量以及target变量的相关性系数
pd.set_option('display.max_columns', 10)

pd.set_option('display.max_rows', 10)
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28',], axis=1)
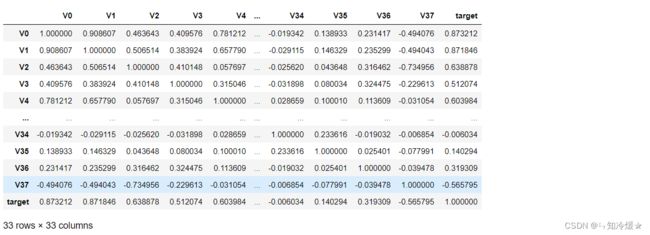
train_corr = data_train1.corr()
train_corr

输出：

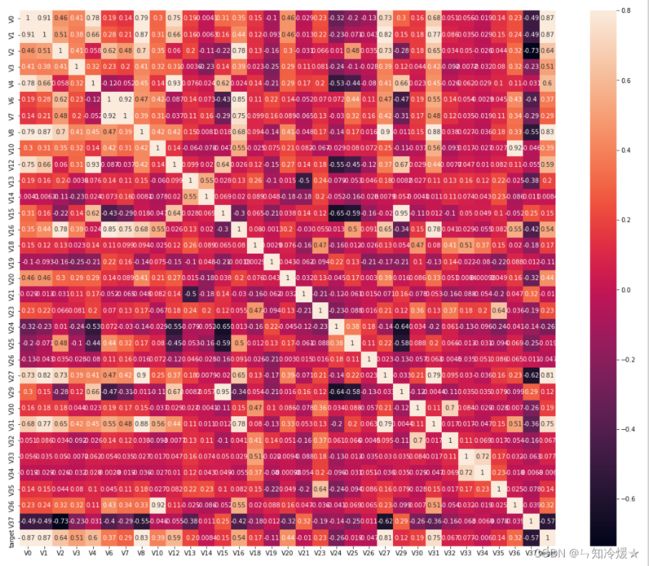
ax = plt.subplots(figsize=(20,16)) 
ax= sns.heatmap(train_corr, vmax=.8, square=True, annot=True)
# 从热力图中可以看出各个特征变量之间的相关性以及它们与target变量的相关性。

输出：

# 这个图看起来不太聪明的样子，先不考虑这个图——————


# 找出相关程度
data_train1 = train_data.drop(['V5','V9','V11','V17','V22','V28'],axis=1)

plt.figure(figsize=(20, 16))  # 指定绘图对象宽度和高度
colnm = data_train1.columns.tolist()  # 列表头
mcorr = data_train1[colnm].corr(method="spearman")  # 相关系数矩阵，即给出了任意两个变量之间的相关系数
mask = np.zeros_like(mcorr, dtype=np.bool)  # 构造与mcorr同维数矩阵 为bool型
mask[np.triu_indices_from(mask)] = True  # 角分线右侧为True
cmap = sns.diverging_palette(220, 10, as_cmap=True)  # 返回matplotlib colormap对象
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  # 热力图（看两两相似度）
plt.show()

输出：

#寻找K个与target变量最相关的特征信息
k = 10 # number of variables for heatmap
cols = train_corr.nlargest(k, 'target')['target'].index

cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10, 10))#调整画布大小
hm = sns.heatmap(train_data[cols].corr(),annot=True,square=True)

plt.show()

输出：

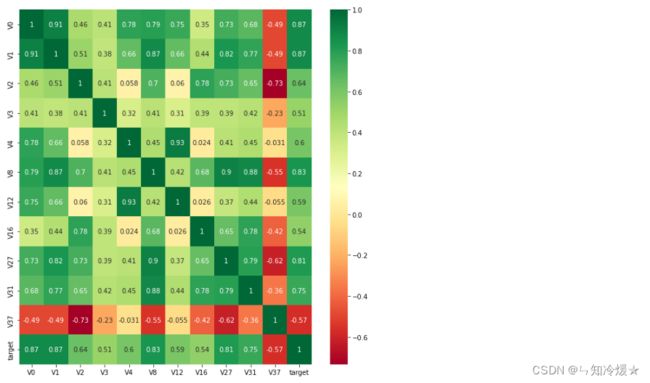
# 找出与target相关性大于0.5的变量
# 简单、直观地判断哪些特征变量线性相关，相关系数越大，就认为这些特征对target变量的线性影响越大。

threshold = 0.5

corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat["target"])>threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot=True,cmap="RdYlGn")

输出：

1-8、Box-Cox变换

drop_columns = ['V5','V9','V11','V17','V22','V28']
# 可以将一些特征删除，这里先不删除这些特征，后续分析会用到。
threshold = 0.5

# Absolute value correlation matrix
corr_matrix = data_train1.corr().abs()
drop_col=corr_matrix[corr_matrix["target"]<threshold].index

#data_all.drop(drop_col, axis=1, inplace=True)

# Box-Cox变换是统计建模中常用的一种数据转换方法，在连续的相应变量不满足正态分布时，可以使用Box-Cox变换，这一变换可以使线性回归模型
# 满足线性、正态性、独立性、方差齐性的同时，又不丢失信息。在对数据做Box-Cox变换之后，可以在一定程度上减小不可观测的误差和预测变量的相关性
# 这有利于线性模型的拟合以及分析出特征的相关性。

# 在做Box-Cox变换之前，需要对数据做归一化预处理。
# 对数据进行合并操作可以使训练数据和测试数据一致。
# 线上部署只需采用训练数据的归一化即可


#merge train_set and test_set
train_x =  train_data.drop(['target'], axis=1)

#data_all=pd.concat([train_data,test_data],axis=0,ignore_index=True)
data_all = pd.concat([train_x,test_data]) 


data_all.drop(drop_columns,axis=1,inplace=True)
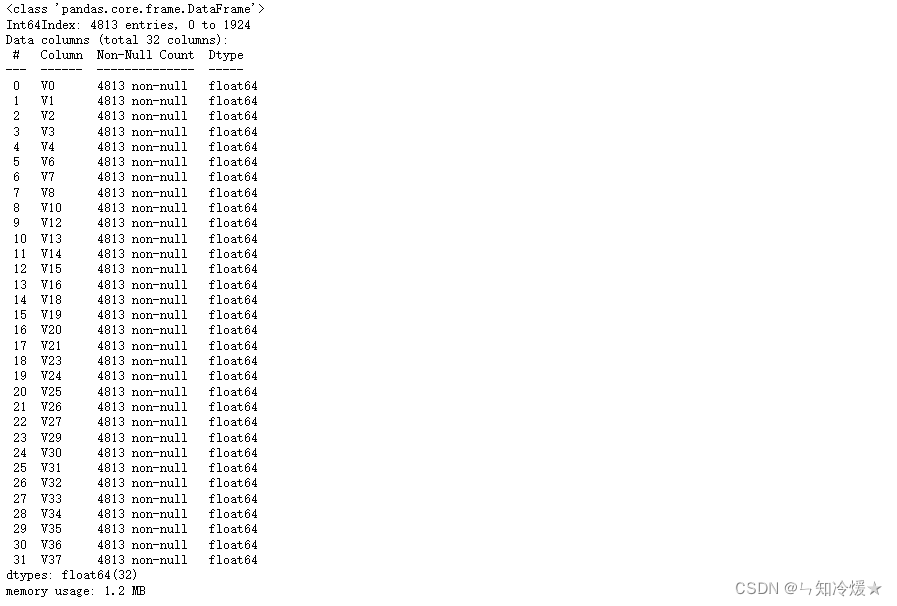
#View data
data_all.info()

输出：

# 对合并后的每列数据进行归一化
# # normalise numeric columns
cols_numeric=list(data_all.columns)

def scale_minmax(col):
    return (col-col.min())/(col.max()-col.min())

data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)
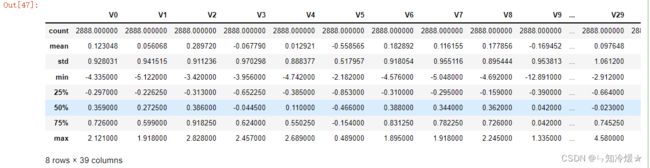
data_all[cols_numeric].describe()

输出：

# 也可以分开对训练数据和测试数据进行归一化处理，不过这种方式需要建立在训练数据和测试数据分布一致的前提下，建议在数据量大的情况下使用。
#col_data_process = cols_numeric.append('target')
train_data_process = train_data[cols_numeric]
train_data_process = train_data_process[cols_numeric].apply(scale_minmax,axis=0)

test_data_process = test_data[cols_numeric]
test_data_process = test_data_process[cols_numeric].apply(scale_minmax,axis=0)

cols_numeric_left = cols_numeric[0:13]
cols_numeric_right = cols_numeric[13:]
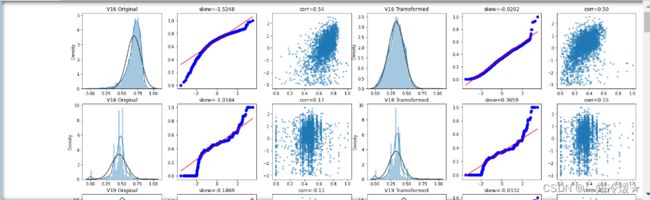
## Check effect of Box-Cox transforms on distributions of continuous variables

train_data_process = pd.concat([train_data_process, train_data['target']], axis=1)

fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4*fcols,4*frows))
i=0

for var in cols_numeric_left:
    dat = train_data_process[[var, 'target']].dropna()
        
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(dat[var] , fit=stats.norm);
    plt.title(var+' Original')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(dat[var], plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(dat[var], dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
 
    i+=1
    plt.subplot(frows,fcols,i)
    trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
    trans_var = scale_minmax(trans_var)      
    sns.distplot(trans_var , fit=stats.norm);
    plt.title(var+' Tramsformed')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(trans_var, plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_var, dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))

输出：

## Check effect of Box-Cox transforms on distributions of continuous variables


fcols = 6
frows = len(cols_numeric_right)
plt.figure(figsize=(4*fcols,4*frows))
i=0

for var in cols_numeric_right:
    dat = train_data_process[[var, 'target']].dropna()
        
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(dat[var] , fit=stats.norm);
    plt.title(var+' Original')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(dat[var], plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(dat[var], dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(dat[var], dat['target'])[0][1]))
 
    i+=1
    plt.subplot(frows,fcols,i)
    trans_var, lambda_var = stats.boxcox(dat[var].dropna()+1)
    trans_var = scale_minmax(trans_var)      
    sns.distplot(trans_var , fit=stats.norm);
    plt.title(var+' Tramsformed')
    plt.xlabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    _=stats.probplot(trans_var, plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
    plt.xlabel('')
    plt.ylabel('')
        
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_var, dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))

输出：

1-9、小结

• 删除训练集和测试集中分布不一致的特征变量,
• 计算特征变量与目标变量的相关性系数并筛选（好像效果没那么好，多多尝试吧！）
• 使用Box-Cox变换可以使线性回归模型在满足线性、正态性、独立性以及方差齐性的同时，又不丢失信息。

二、模型训练

2-1、导入数据分析工具包、数据读取

# 忽略pandas的错误提示。
import os
os.environ["KMP_DUPLICATE_LIB_OK"]  =  "TRUE"

# 导入数据分析的各种工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import r2_score
from scipy import stats

import warnings
warnings.filterwarnings("ignore")
 
%matplotlib inline

# 数据读取
train_data_file = "./zhengqi_train.txt"
test_data_file =  "./zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

# 数据预览
train_data.describe()

输出：

2-2、异常值分析

plt.figure(figsize=(18, 10))
plt.boxplot(x=train_data.values,labels=train_data.columns)
plt.hlines([-7.5, 7.5], 0, 40, colors='g')
plt.show()

输出：

• 注意：这里特征V9的异常值可以考虑删除，但是呢，有时候删除了不一定效果就好，所以还是需要多多尝试啦。

2-3、训练集、测试集的最大值最小值归一化

from sklearn import preprocessing 

features_columns = [col for col in train_data.columns if col not in ['target']]
min_max_scaler = preprocessing.MinMaxScaler()
min_max_scaler = min_max_scaler.fit(train_data[features_columns])
train_data_scaler = min_max_scaler.transform(train_data[features_columns])

# min_max_scaler = min_max_scaler.fit(test_data[features_columns])
test_data_scaler = min_max_scaler.transform(test_data[features_columns])
train_data_scaler = pd.DataFrame(train_data_scaler)
train_data_scaler.columns = features_columns
test_data_scaler = pd.DataFrame(test_data_scaler)
test_data_scaler.columns = features_columns
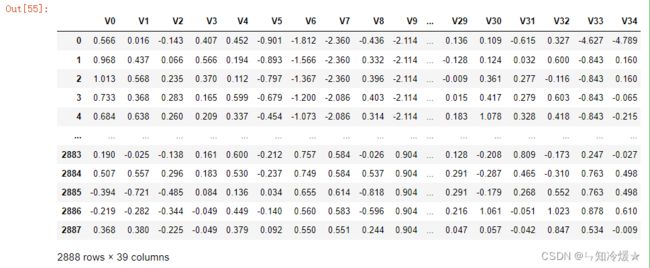
train_data_scaler['target'] = train_data['target']

train_data

• Tips：归一化可以让模型更好的拟合数据。

输出：

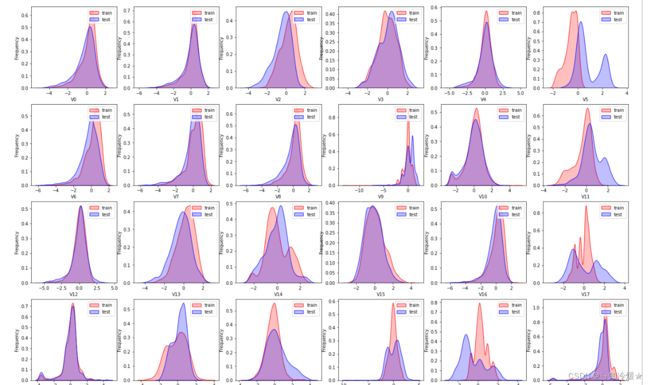
2-4、查看训练集和测试集数据分布情况

dist_cols = 6
dist_rows = len(test_data_scaler.columns)

plt.figure(figsize=(4*dist_cols,4*dist_rows))


for i, col in enumerate(test_data_scaler.columns):
    ax=plt.subplot(dist_rows,dist_cols,i+1)
    ax = sns.kdeplot(train_data_scaler[col], color="Red", shade=True)
    ax = sns.kdeplot(test_data_scaler[col], color="Blue", shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax = ax.legend(["train","test"])
 
plt.show()

输出：

• Tips：分布不一致怎么办？当然是选择原谅他咯！开玩笑，太离谱的分布该删还是得删掉。

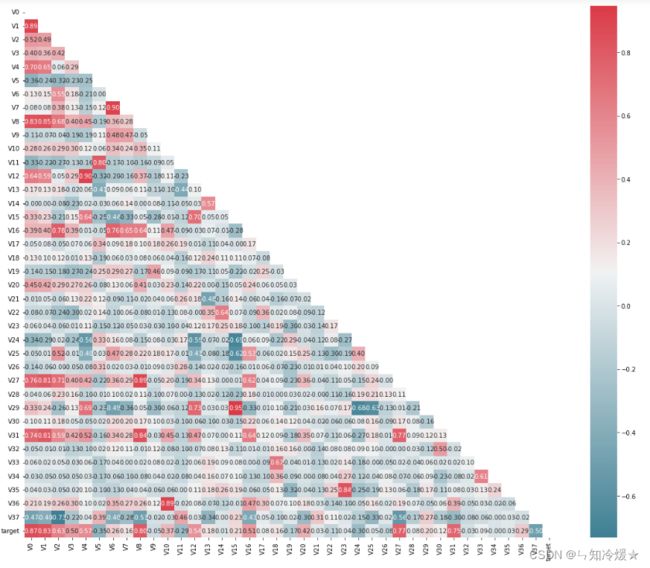
2-5、查看特征相关性

plt.figure(figsize=(20, 16))  
column = train_data_scaler.columns.tolist()  
mcorr = train_data_scaler[column].corr(method="spearman")  
mask = np.zeros_like(mcorr, dtype=np.bool)  
mask[np.triu_indices_from(mask)] = True  
cmap = sns.diverging_palette(220, 10, as_cmap=True)  
g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')  
plt.show()

输出：

2-6、相关性分析

mcorr=mcorr.abs()
numerical_corr=mcorr[mcorr['target']>0.1]['target']
print(numerical_corr.sort_values(ascending=False))

index0 = numerical_corr.sort_values(ascending=False).index
print(train_data_scaler[index0].corr('spearman'))

# 相关性筛选， 把相关性大于0.3的都拿出来。
features_corr = numerical_corr.sort_values(ascending=False).reset_index()
features_corr.columns = ['features_and_target', 'corr']
features_corr_select = features_corr[features_corr['corr']>0.3] # 筛选出大于相关性大于0.3的特征
print(features_corr_select)
select_features = [col for col in features_corr_select['features_and_target'] if col not in ['target']]
new_train_data_corr_select = train_data_scaler[select_features+['target']]
new_test_data_corr_select = test_data_scaler[select_features]

输出：

2-7、多重共线性分析

多重共线性：

• 在进行线性回归分析时，容易出现自变量（解释变量）之间彼此相关的现象，我们称这种现象为多重共线性。
• 如果模型仅用于预测，则只要拟合程度好，可不处理多重共线性问题，存在多重共线性的模型用于预测时，往往不影响预测结果。

from statsmodels.stats.outliers_influence import variance_inflation_factor #多重共线性方差膨胀因子
#多重共线性
new_numerical=['V0', 'V2', 'V3', 'V4', 'V5', 'V6', 'V10','V11', 
                         'V13', 'V15', 'V16', 'V18', 'V19', 'V20', 'V22','V24','V30', 'V31', 'V37']
X=np.matrix(train_data_scaler[new_numerical])
VIF_list=[variance_inflation_factor(X, i) for i in range(X.shape[1])]
VIF_list

输出：

2-8、PCA去除多重共线性、降维

from sklearn.decomposition import PCA   #主成分分析法

#PCA方法降维
#保持90%的信息
pca = PCA(n_components=0.95)
new_train_pca_90 = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_90 = pca.transform(test_data_scaler)
new_train_pca_90 = pd.DataFrame(new_train_pca_90)
new_test_pca_90 = pd.DataFrame(new_test_pca_90)
new_train_pca_90['target'] = train_data_scaler['target']
new_train_pca_90.describe()

输出：

#PCA方法降维
#保留16个主成分
pca = PCA(n_components=37)
new_train_pca_16 = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_16 = pca.transform(test_data_scaler)
new_train_pca_16 = pd.DataFrame(new_train_pca_16)
new_test_pca_16 = pd.DataFrame(new_test_pca_16)
new_train_pca_16['target'] = train_data_scaler['target']
new_train_pca_16.describe()

• 注意：到模型训练为止，前面用到的使用箱型图来进行异常值分析、使用kde图来看分布，使用热力图来看特征和目标的相关性，使用多重共线性函数来看特征之间的相关性，这些方法都只是用来进行一个数据的分析，即使遇到了异常，也没有进行一个实际的处理，所以前面的这些方法，都可以作为一个调参的依据，在本次实验中，实际用到的只有归一化和使用PCA降维（其中PCA降维又分为按照特征个数降维和按照比例来降低维度）

2-9、模型训练（导库、切分训练集和验证集）

from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.neighbors import KNeighborsRegressor  #K近邻回归
from sklearn.tree import DecisionTreeRegressor     #决策树回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.svm import SVR  #支持向量回归
import lightgbm as lgb #lightGbm模型

from sklearn.model_selection import train_test_split # 切分数据
from sklearn.metrics import mean_squared_error #评价指标

from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit

#采用 pca 保留16维特征的数据
new_train_pca_16 = new_train_pca_16.fillna(0)
train = new_train_pca_16[new_test_pca_16.columns]
target = new_train_pca_16['target']

# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

# 也可以采用保留百分之90的方法。
# new_train_pca_90 = new_train_pca_90.fillna(0)
# train = new_train_pca_90[new_test_pca_90.columns]
# target = new_train_pca_90['target']

# # 切分数据 训练数据80% 验证数据20%
# train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

2-10、定义绘制模型学习曲线函数

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
                        n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
    '''
    定义画出学习曲线的方法，核心是调用learning_curve方法。
    '''
    plt.figure()
    plt.title(title)
    
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel("Training examples")
    plt.ylabel("Score")
    # 这里交叉验证调用的必须是ShuffleSplit。
    # n_jobs： 要并行运行的作业数，这里默认为1，如果-1则表示使用所有处理器。
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
    # 返回值：
    
    # train_sizes: 训练示例的等分比例，代表着横坐标有几个点。
    # train_scores： 训练集得分: 二维数组，shape:(5, 100)
    # test_scores：测试集得分
    # print(train_scores)
    # print(test_scores)
    
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    
    print(train_sizes)
    print(train_scores_mean)
    print(test_scores_mean)
    
    plt.grid()
 
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1, color="g")
    
    plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
             label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
    plt.legend(loc="best")
    return plt

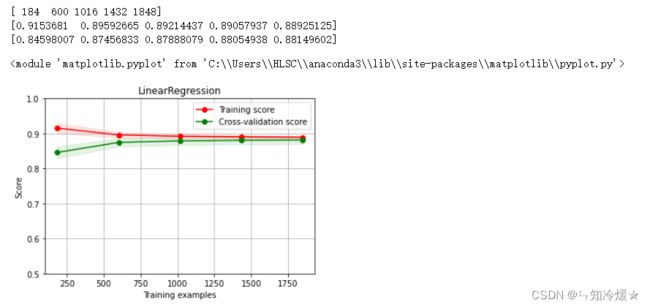
2-11、多元线性回归模型&绘制线性回归模型学习曲线

clf = LinearRegression()
clf.fit(train_data, train_target)
# 
score = mean_squared_error(test_target, clf.predict(test_data))
print("LinearRegression:   ", score)
r2_score(test_target, clf.predict(test_data))


X = train_data.values
y = train_target.values
# 图一
title = r"LinearRegression"

# ShuffleSplit：将样例打散，随机取出20%的数据作为测试集，这样取出100次，
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = LinearRegression()    #建模
plot_learning_curve(estimator, title, X, y, ylim=(0.5, 1), cv=cv, n_jobs=1)

输出：

# 删除异常值、归一化处理 保留16个特征处理
# LinearRegression:    0.2716689554157152
# 删除异常值、归一化处理 保留32个特征处理
# LinearRegression:    0.24770401603781597
# 删除异常值、归一化处理 保留37个特征处理
# LinearRegression:    0.24097484781481712

# 删除异常值、归一化处理 保留0.9特征
# LinearRegression:    0.2716958270664696
# 删除异常值、归一化处理 保留0.9特征，删除掉5 9 11 等特征
# LinearRegression:    0.2801651140485663
# 删除异常值、归一化处理 保留0.95特征，删除掉5 9 11 等特征
# LinearRegression:    0.2681738269068221
# 删除异常值、归一化处理 保留0.95特征
# LinearRegression:    0.26423379176281725

# 不删除异常值！ 归一化处理 保留37个特征处理
# LinearRegression:    0.1158780917760841

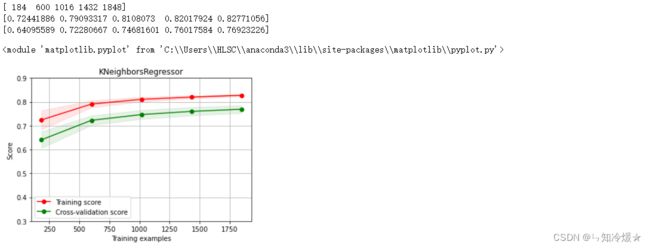
2-12、K近邻回归&绘制K近邻回归学习曲线

clf = KNeighborsRegressor(n_neighbors=7) # 最近三个
clf.fit(train_data, train_target)
score = mean_squared_error(test_target, clf.predict(test_data))
print(i)
print("KNeighborsRegressor:   ", score)
r2_score(test_target, clf.predict(test_data))

X = train_data.values
y = train_target.values
 
# K近邻回归
title = r"KNeighborsRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = KNeighborsRegressor(n_neighbors=8)    #建模
plot_learning_curve(estimator, title, X, y, ylim=(0.3, 0.9), cv=cv, n_jobs=1)

输出：

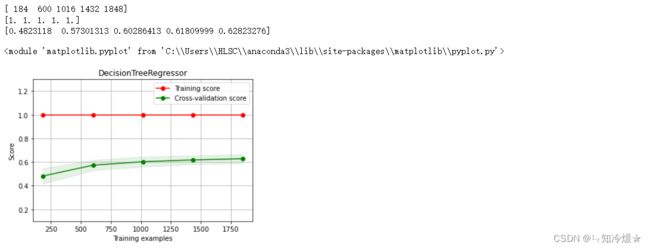
2-13、决策树回归&绘制决策树学习曲线

• 决策树回归可以理解为根据一定准则，将一个空间划分为若干个子空间，然后利用子空间内所有点的信息表示这个子空间的值。
• 如何预测？ 我们可以利用这些划分区域的均值或者中位数代表这个区域的预测值，一旦有样本点按照划分规则落入某一个区域，就直接利用该区域的均值或者中位数代表其预测值。

clf = DecisionTreeRegressor() 
clf.fit(train_data, train_target)

score = mean_squared_error(test_target, clf.predict(test_data))
print("DecisionTreeRegressor:   ", score)
r2_score(test_target, clf.predict(test_data))


X = train_data.values
y = train_target.values
 
# 决策树回归
title = r"DecisionTreeRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = DecisionTreeRegressor()    #建模
plot_learning_curve(estimator, title, X, y, ylim=(0.1, 1.3), cv=cv, n_jobs=1)

输出：

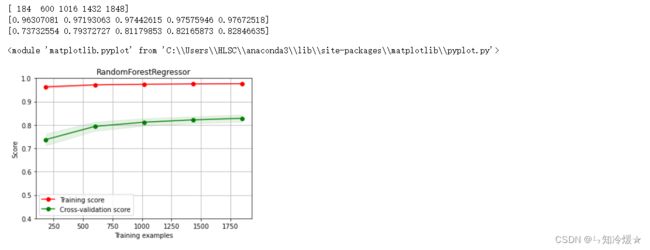
2-14、随机森林回归&绘制随机森林回归学习曲线

clf = RandomForestRegressor(n_estimators=200) # 200棵树模型
clf.fit(train_data, train_target)
score = mean_squared_error(test_target, clf.predict(test_data))
print("RandomForestRegressor:   ", score)
r2_score(test_target, clf.predict(test_data))


X = train_data.values
y = train_target.values
 
title = r"RandomForestRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = RandomForestRegressor(n_estimators=200)    #建模
plot_learning_curve(estimator, title, X, y, ylim=(0.4, 1.0), cv=cv, n_jobs=1)

输出：

2-15、lgb模型回归&绘制lgb回归学习曲线

# lgb回归模型
clf = lgb.LGBMRegressor(
        learning_rate=0.01,
        max_depth=-1,
        n_estimators=5000,
        boosting_type='gbdt',
        random_state=2019,
        objective='regression',
    ) 

# 训练模型
clf.fit(
        X=train_data, y=train_target,
        eval_metric='MSE',
        verbose=50
    )

score = mean_squared_error(test_target, clf.predict(test_data))
print("lightGbm:   ", score)

X = train_data.values
y = train_target.values
 
# K近邻回归
title = r"LGBMRegressor"
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = lgb.LGBMRegressor(
    learning_rate=0.01,
    max_depth=-1,
    n_estimators=100,
    boosting_type='gbdt',
    random_state=2019,
    objective='regression'
    )    #建模

plot_learning_curve(estimator, title, X, y, ylim=(0.4, 1.0), cv=cv, n_jobs=1)

输出：

三、模型验证

四、特征优化

五、模型融合

参考文章：
官方链接.

---

总结

好长好长好长。明天就是国庆啦啦啦啦！