朴素贝叶斯python复现(基于数据集iris)
@朴素贝叶斯算法Python复现(基于iris数据集)TOC
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 一、朴素贝叶斯分类器
- 三、朴素贝叶斯分类器python代码
-
- 1.引入库
- 2.读取数据集并根据标签值分类
- 3.定义均值和方差
- 4.构建朴素贝叶斯分类器
- 5.完整代码里面数据集处理代码讲解
- 6.最后根据测试集进行预测以及计算Accuracy
- 总结
前言
本节主要讲的是朴素贝叶斯算法以及相应的Python复现(基于iris的数据集)。本段代码没有进行K折交叉验证,希望有需要的读者可以自行添加,如果对其他数据集有分类情况偏低,可以考虑添加一下拉普拉斯修正,或者对数据进行归一化处理。
接下来,对朴素贝叶斯定理做一个简单的介绍,如果需要了解详细内容可以找相关资料进行学习
一、朴素贝叶斯分类器
1.贝叶斯分类 :是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。本文作为分类算法的第一篇,将首先介绍分类问题,对分类问题进行一个正式的定义。然后,介绍贝叶斯分类算法的基础——贝叶斯定理。最后,通过实例讨论贝叶斯分类中最简单的一种:朴素贝叶斯分类。
2.朴素贝叶斯定理:
![]()
表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率
![]()
3.拉普拉斯修正:
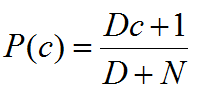
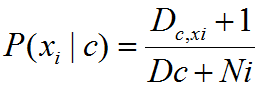
拉普拉斯修正:为了避免其他属性携带的信息被训练集中未出现的属性抹去,在估计概率值时通常要进行smoothing,常使用拉普拉斯修正。具体来说,令N表示训练集D中可能的类别数,Ni表示第i个属性可能的取值数。
三、朴素贝叶斯分类器python代码
1.引入库
pandas:exce表数据集的读取
shuffle:数据集打乱顺序
exp:自然指数e
import pandas as pd
import numpy as np
from math import pi
from numpy import exp
from sklearn.utils import shuffle
2.读取数据集并根据标签值分类
此处主要是将不同属性的三个标签用字典进行分类
返回的每一个dict都是3个标签的同一个属性的数据
fpath = r'd:iris.xls'
object = pd.read_excel(fpath)
object = shuffle(object)
list = []
dict1 = {}
dict2 = {}
dict3 = {}
dict4 = {}
i1 = object.iloc[100:150,0:5]
test_set = i1.values.tolist()#测试集
#.....................................................................................
m1 = object.iloc[0:100, [0, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict1:
dict1[j[1]] = [j[0]]
else:
dict1[j[1]].append(j[0])
print(dict1)
m1 = object.iloc[0:100, [1, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict2:
dict2[j[1]] = [j[0]]
else:
dict2[j[1]].append(j[0])
m1 = object.iloc[0:100, [2, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict3:
dict3[j[1]] = [j[0]]
else:
dict3[j[1]].append(j[0])
m1 = object.iloc[0:100, [3, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict4:
dict4[j[1]] = [j[0]]
else:
dict4[j[1]].append(j[0])
return dict1,dict2,dict3,dict4,test_set
![]()
这个是第一个属性分类后dict1相应的返回值,test_set是测试集的数据集合。
3.定义均值和方差
输入的per_dataset是每一个数据的数据
def average_variance(per_dataset):
'''
:param per_dataset:
:return:[average]
'''
average_num = sum(per_dataset)/len(per_dataset)
value = 0
list1 = []
for i in per_dataset:
value = value + (i - average_num) ** 2
variance_value = value / (len(per_dataset) - 1)
return [average_num],variance_value
4.构建朴素贝叶斯分类器
def Naive_Bayesian(xi,average,variance):
'''
朴素贝叶斯算法构建的过程
:param xi:测试集的属性值
:param average: 训练集该属性的平均值
:param variance: 训练集该属性的方差
:return: p(xi|c)
'''
p_xi_c = (1 / (((2 * pi) ** 0.5) * variance)) * exp(-(xi - average) ** 2 /(2 * variance))
p =constant_data(xi,average,variance)
return p
5.完整代码里面数据集处理代码讲解
得到的是每一列属性对应的三个标签,以及对应的四个属性值的列表。下面会有相应的dict_var1输出值和total_dict_var
dict1, dict2, dict3, dict4, test_set = get_dataset()
total_dict_var=[]
dict_var1 = []
dict_var2 = []
dict_var3 = []
dict_var4 = []
for i in range(1,4):#dict1:第一个属性对应1.0,2.0,3.0标签的列表集合
average_1,variance_1 = average_variance(dict1[i])
average_1.append((variance_1))
dict_var1.append(average_1)
print('接下来输出的是三个标签对应的第一个属性的[均值,方差]形式的列表集合')
print(dict_var1)
total_dict_var.append(dict_var1)
#print(total_dict_var)
for i in range(1,4):#dict2:第二个属性对应1.0,2.0,3.0标签的列表集合
average_2,variance_2 = average_variance(dict2[i])
average_2.append(variance_2)
dict_var2.append(average_2)
total_dict_var.append(dict_var2)
for i in range(1,4):#dict3:第三个属性对应1.0,2.0,3.0标签的集合
average_3,varince_3 =average_variance(dict3[i])
average_3.append(varince_3)
dict_var3.append(average_3)
total_dict_var.append(dict_var3)
for i in range(1,4):#dict4:第四个属性对应1.0,2.0,3.0标签的集合
average_4,varince_4 = average_variance(dict4[i])
average_4.append(varince_4)
dict_var4.append(average_4)
total_dict_var.append(dict_var4)
print("接下来是total_dict_var(每一列存在三个标签,共四列")
print(np.array(total_dict_var))#每一列存在三个标签 共存在4列
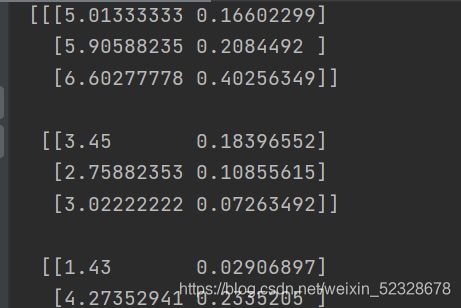
输出的是一个4*3的矩阵每一行表示的对应属性的三个标签的average均值和variance方差的值的列表
6.最后根据测试集进行预测以及计算Accuracy
correct_num =0 #计数器,预测正确下面会自动+1
for sample in test_set:
result = []#此处是每个样例对应的 假设值(1.0,2.0,3.0)对应的相对概率值,之后会根据返回最大值的下标+1来进行预测的过程
for i in range(0,4):
xi = sample[i]
for j in range(0,3):
averaging = total_dict_var[i][j][0]
variancing = total_dict_var[i][j][1]
p_type =len(dict1[j+1])/(len(dict1[2])+len(dict1[1])+len(dict1[3])) #此处计算的是p(c)
Navi1 = Naive_Bayesian(xi,averaging,variancing)
result.append(Navi1)
# print(result)
k = []
o = []
for j in range(0,3):
p_type = (len(dict1[j + 1])) / (len(dict1[2]) + len(dict1[1]) + len(dict1[3]))#+1和+len(dict1[j+1])拉普拉斯修正
o.append(p_type)
#print(o)
for i in range(0,3):
k.append((result[i]*result[i+3]*result[i+6]+result[i+9])*o[i])#得到的列表里每个标签的属性间隔的下标是3 根据公式将其连乘
#print(k)
index_end = k.index(max(k))+1 #列表里面排列的是三个标签值对应的p,排列顺序就是1.0,2.0,3.0,可以根据(index+1)来预测标签
#print(index_end)
if index_end == sample[4]: #比较预测预测值和实际值
correct_num =correct_num+1 #同上面的计数器,正确则+1
Accuracy1 = correct_num/len(test_set) #计算正确的概率
print("Final Accuracy ={}".format(Accuracy1))
总结
以下是完整的代码块,iris数据集可以到sklearn库里面调取
'''
@Time : 2021/4/21
@Author : Jupiter (朱比特)
@FileName: Navie_Bayes.py
@Blog :https://blog.csdn.net/qq_1067857137
欢迎大家一起交流!!!
'''
import pandas as pd
import numpy as np
from math import pi
from numpy import exp
from sklearn.utils import shuffle
def average_variance(per_dataset):
'''
:param per_dataset:
:return:[average]
'''
average_num = sum(per_dataset)/len(per_dataset)
value = 0
list1 = []
for i in per_dataset:
value = value + (i - average_num) ** 2
variance_value = value / (len(per_dataset) - 1)
return [average_num],variance_value
def get_dataset():
'''
获取数据集
:return: dict的值是每一个属性对应的分类的列表集合如{1.0:[],2.0:[],3.0:[]},test_set指的是测试集
里面shuffle的作用是打乱数据集的顺序
我采用的是pandas的方式来读取excel表的数据集
'''
fpath = r'd:iris.xls'
object = pd.read_excel(fpath)
object = shuffle(object)
list = []
dict1 = {}
dict2 = {}
dict3 = {}
dict4 = {}
i1 = object.iloc[100:150,0:5]
test_set = i1.values.tolist()#测试集
#.....................................................................................
m1 = object.iloc[0:100, [0, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict1:
dict1[j[1]] = [j[0]]
else:
dict1[j[1]].append(j[0])
print(dict1)
m1 = object.iloc[0:100, [1, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict2:
dict2[j[1]] = [j[0]]
else:
dict2[j[1]].append(j[0])
m1 = object.iloc[0:100, [2, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict3:
dict3[j[1]] = [j[0]]
else:
dict3[j[1]].append(j[0])
m1 = object.iloc[0:100, [3, 4]]
m2 = m1.values.tolist()
for j in m2:
if j[1] not in dict4:
dict4[j[1]] = [j[0]]
else:
dict4[j[1]].append(j[0])
return dict1,dict2,dict3,dict4,test_set
def constant_data(xi,average,variance):
'''
此处是连续值,并且返回p(xi|c)
:param xi: 指的是待预测的属性值
:param average: 训练集该属性的平均值
:param variance: 训练集该属性的方差
:return:p(xi|c)
'''
p_xi_c = (1/(((2*pi)**0.5)*variance))*exp(-(xi-average)**2/(2*variance))
return p_xi_c
def Naive_Bayesian(xi,average,variance):
'''
朴素贝叶斯算法构建的过程
:param xi:测试集的属性值
:param average: 训练集该属性的平均值
:param variance: 训练集该属性的方差
:return: p(xi|c)
'''
p_xi_c = (1 / (((2 * pi) ** 0.5) * variance)) * exp(-(xi - average) ** 2 /(2 * variance))
p =constant_data(xi,average,variance)
return p
if __name__ == '__main__':
dict1, dict2, dict3, dict4, test_set = get_dataset()
total_dict_var=[]
dict_var1 = []
dict_var2 = []
dict_var3 = []
dict_var4 = []
for i in range(1,4):#dict1:第一个属性对应1.0,2.0,3.0标签的列表集合
average_1,variance_1 = average_variance(dict1[i])
average_1.append((variance_1))
dict_var1.append(average_1)
print('接下来输出的是三个标签对应的第一个属性的[均值,方差]形式的列表集合')
print(dict_var1)
total_dict_var.append(dict_var1)
#print(total_dict_var)
for i in range(1,4):#dict2:第二个属性对应1.0,2.0,3.0标签的列表集合
average_2,variance_2 = average_variance(dict2[i])
average_2.append(variance_2)
dict_var2.append(average_2)
total_dict_var.append(dict_var2)
for i in range(1,4):#dict3:第三个属性对应1.0,2.0,3.0标签的集合
average_3,varince_3 =average_variance(dict3[i])
average_3.append(varince_3)
dict_var3.append(average_3)
total_dict_var.append(dict_var3)
for i in range(1,4):#dict4:第四个属性对应1.0,2.0,3.0标签的集合
average_4,varince_4 = average_variance(dict4[i])
average_4.append(varince_4)
dict_var4.append(average_4)
total_dict_var.append(dict_var4)
print("接下来是total_dict_var(每一列存在三个标签,共四列")
print(np.array(total_dict_var))#每一列存在三个标签 共存在4列
#result = [] ->这个列表必须放在循环里面不然列表不会更新
correct_num =0 #计数器,预测正确下面会自动+1
for sample in test_set:
result = []#此处是每个样例对应的 假设值(1.0,2.0,3.0)对应的相对概率值,之后会根据返回最大值的下标+1来进行预测的过程
for i in range(0,4):
xi = sample[i]
for j in range(0,3):
averaging = total_dict_var[i][j][0]
variancing = total_dict_var[i][j][1]
p_type =len(dict1[j+1])/(len(dict1[2])+len(dict1[1])+len(dict1[3])) #此处计算的是p(c)
Navi1 = Naive_Bayesian(xi,averaging,variancing)
result.append(Navi1)
# print(result)
k = []
o = []
for j in range(0,3):
p_type = (len(dict1[j + 1])) / (len(dict1[2]) + len(dict1[1]) + len(dict1[3]))#+1和+len(dict1[j+1])拉普拉斯修正
o.append(p_type)
#print(o)
for i in range(0,3):
k.append((result[i]*result[i+3]*result[i+6]+result[i+9])*o[i])#得到的列表里每个标签的属性间隔的下标是3 根据公式将其连乘
#print(k)
index_end = k.index(max(k))+1 #列表里面排列的是三个标签值对应的p,排列顺序就是1.0,2.0,3.0,可以根据(index+1)来预测标签
#print(index_end)
if index_end == sample[4]: #比较预测预测值和实际值
correct_num =correct_num+1 #同上面的计数器,正确则+1
Accuracy1 = correct_num/len(test_set) #计算正确的概率
print("Final Accuracy ={}".format(Accuracy1))
当然如果能进行十折交叉验证实验效果会更好。
这里是一次测试的准确率:一般在90%-97%之间

周志华《机器学习》